Dieser Artikel behandelt die Taylorformel, also die Darstellung von Funktionen durch ein endliches Taylorpolynom und ein Restglied. Für die Darstellung von Funktionen durch den Grenzwert der Taylorpolynome siehe
Taylorreihe .
Die Taylor-Formel (auch Satz von Taylor ) ist ein Resultat aus dem mathematischen Teilgebiet der Analysis . Sie ist benannt nach dem Mathematiker Brook Taylor . Man kann diese Formel verwenden, um Funktionen in der Umgebung eines Punktes durch Polynome , die sogenannten Taylorpolynome [ 1] anzunähern . Man spricht auch von der Taylor-Näherung . Die Taylor-Formel ist aufgrund ihrer relativ einfachen Anwendbarkeit und Nützlichkeit ein Hilfsmittel in vielen Ingenieur- , Sozial- und Naturwissenschaften geworden. So kann ein komplizierter analytischer Ausdruck durch ein Taylorpolynom geringen Grades (oftmals gut) angenähert werden, z. B. in der Physik oder bei der Ausgleichung geodätischer Netze. Die oft verwendete Kleinwinkelnäherung des Sinus ist eine nach dem ersten Glied abgebrochene Taylorreihe dieser Funktion.
Eng verwandt mit der Taylor-Formel ist die sogenannte Taylorreihe (Taylor-Entwicklung).
Eine Näherung für eine differenzierbare Funktion
f
{\displaystyle f}
a
{\displaystyle a}
Gerade , also durch ein Polynom 1. Grades, ist gegeben durch die Tangente mit der Gleichung
T
1
f
(
x
;
a
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
{\displaystyle T_{1}f(x;a)=f(a)+f'(a)(x-a)}
Sie lässt sich dadurch charakterisieren, dass an der Stelle
x
=
a
{\displaystyle x=a}
f
(
x
)
{\displaystyle f(x)}
T
1
f
(
x
;
a
)
{\displaystyle T_{1}f(x;a)}
f
(
a
)
=
T
1
f
(
a
;
a
)
,
f
′
(
a
)
=
T
1
′
f
(
a
;
a
)
{\displaystyle f(a)=T_{1}f(a;a),f'(a)=T_{1}'f(a;a)}
Wenn man den Rest
R
1
f
(
x
;
a
)
:=
f
(
x
)
−
T
1
f
(
x
;
a
)
{\displaystyle R_{1}f(x;a):=f(x)-T_{1}f(x;a)}
f
(
x
)
=
T
1
f
(
x
;
a
)
+
R
1
f
(
x
;
a
)
{\displaystyle f(x)=T_{1}f(x;a)+R_{1}f(x;a)}
T
1
f
(
x
;
a
)
{\displaystyle T_{1}f(x;a)}
f
{\displaystyle f}
x
=
a
{\displaystyle x=a}
(
1
)
lim
x
→
a
R
1
f
(
x
;
a
)
x
−
a
=
lim
x
→
a
f
(
x
)
−
T
1
f
(
x
;
a
)
x
−
a
=
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
−
f
′
(
a
)
=
0
{\displaystyle (1)~\lim _{x\to a}{\frac {R_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-T_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}-f'(a)=0}
Definition der Ableitung ).Man kann vermuten, dass man für zweimal differenzierbares
f
{\displaystyle f}
quadratisches Polynom
T
2
f
(
x
;
a
)
{\displaystyle T_{2}f(x;a)}
T
2
″
f
(
a
;
a
)
=
f
″
(
a
)
{\displaystyle T_{2}''f(a;a)=f''(a)}
Ansatz
T
2
f
(
x
;
a
)
=
a
0
+
a
1
(
x
−
a
)
+
a
2
(
x
−
a
)
2
{\displaystyle T_{2}f(x;a)=a_{0}+a_{1}(x-a)+a_{2}(x-a)^{2}}
a
0
=
f
(
a
)
,
a
1
=
f
′
(
a
)
{\displaystyle a_{0}=f(a),a_{1}=f'(a)}
a
2
=
1
2
f
″
(
a
)
{\displaystyle a_{2}={\frac {1}{2}}f''(a)}
T
2
f
(
x
;
a
)
=
f
(
a
)
+
f
′
(
a
)
(
x
−
a
)
+
1
2
f
″
(
a
)
(
x
−
a
)
2
{\displaystyle T_{2}f(x;a)=f(a)+f'(a)(x-a)+{\frac {1}{2}}f''(a)(x-a)^{2}}
Diese Näherungsfunktion bezeichnet man auch als Schmiegparabel.
Man definiert nun dazu den passenden Rest
R
2
f
(
x
;
a
)
:=
f
(
x
)
−
T
2
f
(
x
;
a
)
{\displaystyle R_{2}f(x;a):=f(x)-T_{2}f(x;a)}
f
(
x
)
=
T
2
f
(
x
;
a
)
+
R
2
f
(
x
;
a
)
{\displaystyle f(x)=T_{2}f(x;a)+R_{2}f(x;a)}
x
=
a
{\displaystyle x=a}
Regel von de L’Hospital ):
lim
x
→
a
R
2
f
(
x
;
a
)
(
x
−
a
)
2
=
lim
x
→
a
f
(
x
)
−
f
(
a
)
−
f
′
(
a
)
(
x
−
a
)
(
x
−
a
)
2
−
1
2
f
″
(
a
)
=
lim
x
→
a
f
′
(
x
)
−
f
′
(
a
)
2
(
x
−
a
)
−
1
2
f
″
(
a
)
=
0
{\displaystyle \lim _{x\to a}{\frac {R_{2}f(x;a)}{(x-a)^{2}}}=\lim _{x\to a}{\frac {f(x)-f(a)-f'(a)(x-a)}{(x-a)^{2}}}-{\frac {1}{2}}f''(a)=\lim _{x\to a}{\frac {f'(x)-f'(a)}{2(x-a)}}-{\frac {1}{2}}f''(a)=0}
gilt.
Dieses Vorgehen lässt sich nun leicht auf Polynome
n
{\displaystyle n}
T
n
(
x
)
{\displaystyle T_{n}(x)}
T
n
f
(
a
;
a
)
=
f
(
a
)
,
T
n
′
f
(
a
;
a
)
=
f
′
(
a
)
,
…
,
T
n
(
n
)
f
(
a
;
a
)
=
f
(
n
)
(
a
)
{\displaystyle T_{n}f(a;a)=f(a),\ T_{n}'f(a;a)=f'(a),\ \ldots ,\ T_{n}^{(n)}f(a;a)=f^{(n)}(a)}
Es ergibt sich
T
n
f
(
x
;
a
)
=
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
⋯
+
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle T_{n}f(x;a)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}
Mit der Regel von de L’Hospital finden wir außerdem:
lim
x
→
a
f
(
x
)
−
T
n
f
(
x
;
a
)
(
x
−
a
)
n
=
lim
x
→
a
f
′
(
x
)
−
T
n
′
f
(
x
;
a
)
n
(
x
−
a
)
n
−
1
{\displaystyle \lim _{x\to a}{\frac {f(x)-T_{n}f(x;a)}{(x-a)^{n}}}=\lim _{x\to a}{\frac {f'(x)-T_{n}'f(x;a)}{n(x-a)^{n-1}}}}
Daher ergibt sich mit vollständiger Induktion über
n
{\displaystyle n}
R
n
f
(
x
;
a
)
=
f
(
x
)
−
T
n
f
(
x
;
a
)
{\displaystyle R_{n}f(x;a)=f(x)-T_{n}f(x;a)}
lim
x
→
a
R
n
f
(
x
;
a
)
(
x
−
a
)
n
=
0
{\displaystyle \lim _{x\to a}{\frac {R_{n}f(x;a)}{(x-a)^{n}}}=0}
Ist
f
{\displaystyle f}
n
{\displaystyle n}
f
(
x
)
=
T
n
f
(
x
;
a
)
+
R
n
f
(
x
;
a
)
=
T
n
f
(
x
;
a
)
+
o
(
|
x
−
a
|
n
)
,
x
→
a
,
{\displaystyle f(x)=T_{n}f(x;a)+R_{n}f(x;a)=T_{n}f(x;a)+o(|x-a|^{n}),\quad x\rightarrow a,}
wobei
o
{\displaystyle o}
Landau-Notation steht. Diese Formel nennt man „qualitative Taylorformel“.
Je näher
x
{\displaystyle x}
a
{\displaystyle a}
T
n
f
(
x
;
a
)
{\displaystyle T_{n}f(x;a)}
unten ) an der Stelle
x
{\displaystyle x}
f
{\displaystyle f}
Im Folgenden wird die Taylor-Formel mit Integralrestglied vorgestellt. Die Taylor-Formel existiert auch in Varianten mit anderem Restglied; diese Formeln folgen jedoch aus der Taylor-Formel mit Integralrestglied. Sie stehen unten im Abschnitt Restgliedformeln .
Sei
I
⊂
R
{\displaystyle I\subset \mathbb {R} }
Intervall und
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
(
n
+
1
)
{\displaystyle (n+1)}
stetig differenzierbare Funktion . In den folgenden Formeln stehen
f
′
,
f
″
,
…
,
f
(
k
)
{\displaystyle f',f'',\dots ,f^{(k)}}
k
{\displaystyle k}
f
{\displaystyle f}
Das
n
{\displaystyle n}
Taylorpolynom an der Entwicklungsstelle
a
∈
I
{\displaystyle a\in I}
T
n
f
(
x
;
a
)
=
∑
k
=
0
n
f
(
k
)
(
a
)
k
!
(
x
−
a
)
k
=
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
…
+
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle {\begin{aligned}T_{n}f(x;a)=&\sum _{k=0}^{n}{f^{(k)}(a) \over k!}(x-a)^{k}\\=&f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\ldots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\end{aligned}}}
Damit gehört es zu den Potenzreihen .
Das
n
{\displaystyle n}
Integralrestglied ist definiert durch:
R
n
f
(
x
;
a
)
=
∫
a
x
(
x
−
t
)
n
n
!
f
(
n
+
1
)
(
t
)
d
t
{\displaystyle R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t}
Für alle
a
{\displaystyle a}
x
{\displaystyle x}
I
{\displaystyle I}
f
(
x
)
=
T
n
f
(
x
;
a
)
+
R
n
f
(
x
;
a
)
=
∑
k
=
0
n
f
(
k
)
(
a
)
k
!
(
x
−
a
)
k
+
∫
a
x
(
x
−
t
)
n
n
!
f
(
n
+
1
)
(
t
)
d
t
{\displaystyle {\begin{aligned}f(x)=&T_{n}f(x;a)+R_{n}f(x;a)\\=&\sum _{k=0}^{n}{f^{(k)}(a) \over k!}(x-a)^{k}+\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t\end{aligned}}}
Der Beweis der Taylor-Formel mit Integralrestglied erfolgt durch vollständige Induktion über
n
{\displaystyle n}
Der Induktionsanfang
n
=
0
{\displaystyle n=0}
Fundamentalsatz der Analysis , angewendet auf die einmal stetig differenzierbare Funktion
f
{\displaystyle f}
f
(
x
)
=
f
(
a
)
+
∫
a
x
f
′
(
t
)
d
t
=
T
0
f
(
x
;
a
)
+
R
0
f
(
x
;
a
)
{\displaystyle f(x)=f(a)+\int \limits _{a}^{x}f'(t)\,\mathrm {d} t=T_{0}f(x;a)+R_{0}f(x;a)}
Der Induktionsschritt
n
→
n
+
1
{\displaystyle n\rightarrow n+1}
n
+
1
{\displaystyle n+1}
n
{\displaystyle n}
partielle Integration . Für
(
n
+
2
)
{\displaystyle (n+2)}
f
{\displaystyle f}
f
(
n
+
1
)
(
a
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
+
R
n
+
1
f
(
x
;
a
)
=
f
(
n
+
1
)
(
a
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
+
∫
a
x
(
x
−
t
)
n
+
1
(
n
+
1
)
!
f
(
n
+
2
)
(
t
)
d
t
=
f
(
n
+
1
)
(
a
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
+
[
(
x
−
t
)
n
+
1
(
n
+
1
)
!
f
(
n
+
1
)
(
t
)
]
t
=
a
t
=
x
−
∫
a
x
−
(
x
−
t
)
n
n
!
f
(
n
+
1
)
(
t
)
d
t
=
(
x
−
a
)
n
+
1
(
n
+
1
)
!
f
(
n
+
1
)
(
a
)
−
(
x
−
a
)
n
+
1
(
n
+
1
)
!
f
(
n
+
1
)
(
a
)
+
R
n
f
(
x
;
a
)
=
R
n
f
(
x
;
a
)
{\displaystyle {\begin{aligned}&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+R_{n+1}f(x;a)\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\int \limits _{a}^{x}{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+2)}(t)\,\mathrm {d} t\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\left[{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+1)}(t)\right]_{t=a}^{t=x}-\int \limits _{a}^{x}{\frac {-(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t\\=&{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)-{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)+R_{n}f(x;a)\\=&R_{n}f(x;a)\end{aligned}}}
und somit
T
n
+
1
f
(
x
;
a
)
+
R
n
+
1
f
(
x
;
a
)
=
T
n
f
(
x
;
a
)
+
R
n
f
(
x
;
a
)
=
f
(
x
)
{\displaystyle T_{n+1}f(x;a)+R_{n+1}f(x;a)=T_{n}f(x;a)+R_{n}f(x;a)=f(x)}
Es gibt außer der Integralformel noch andere Darstellungen des Restgliedes.
Nach dem Mittelwertsatz der Integralrechnung ergibt sich für jede natürliche Zahl
p
{\displaystyle p}
1
≤
p
≤
n
+
1
{\displaystyle 1\leq p\leq n+1}
ξ
{\displaystyle \xi }
a
{\displaystyle a}
x
{\displaystyle x}
∫
a
x
f
(
n
+
1
)
(
t
)
(
x
−
t
)
n
+
1
−
p
n
!
⋅
(
x
−
t
)
p
−
1
d
t
=
f
(
n
+
1
)
(
ξ
)
(
x
−
ξ
)
n
+
1
−
p
n
!
⋅
∫
a
x
(
x
−
t
)
p
−
1
d
t
⏟
=
(
x
−
a
)
p
p
{\displaystyle \int \limits _{a}^{x}{f^{(n+1)}(t){\frac {(x-t)^{n+1-p}}{n!}}\cdot (x-t)^{p-1}\,\mathrm {d} t}={\frac {f^{(n+1)}(\xi )(x-\xi )^{n+1-p}}{n!}}\cdot \underbrace {\int \limits _{a}^{x}{(x-t)^{p-1}\,\mathrm {d} t}} _{={\frac {(x-a)^{p}}{p}}}}
Damit folgt die Schlömilchsche Restgliedform
R
n
f
(
x
;
a
)
=
∫
a
x
(
x
−
t
)
n
n
!
f
(
n
+
1
)
(
t
)
d
t
=
f
(
n
+
1
)
(
ξ
)
p
⋅
n
!
(
x
−
ξ
)
n
+
1
−
p
(
x
−
a
)
p
{\displaystyle R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t={\frac {f^{(n+1)}(\xi )}{p\cdot n!}}(x-\xi )^{n+1-p}(x-a)^{p}}
für ein
ξ
{\displaystyle \xi }
a
{\displaystyle a}
x
{\displaystyle x}
Ein Spezialfall, nämlich der mit
p
=
1
{\displaystyle p=1}
Cauchy :
R
n
f
(
x
;
a
)
=
f
(
n
+
1
)
(
ξ
)
n
!
(
x
−
ξ
)
n
(
x
−
a
)
{\displaystyle R_{n}f(x;a)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}(x-a)}
für ein
ξ
{\displaystyle \xi }
a
{\displaystyle a}
x
{\displaystyle x}
Im Spezialfall
p
=
n
+
1
{\displaystyle p=n+1}
Lagrangesche Restglied
R
n
f
(
x
;
a
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
{\displaystyle R_{n}f(x;a)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}}
für ein
ξ
{\displaystyle \xi }
a
{\displaystyle a}
x
{\displaystyle x}
(
n
+
1
)
{\displaystyle (n+1)}
f
{\displaystyle f}
Mit der Taylorformel mit Lagrange-Restglied erhält man für
n
{\displaystyle n}
f
{\displaystyle f}
f
(
x
)
=
T
n
−
1
f
(
x
;
a
)
+
f
(
n
)
(
ξ
)
n
!
(
x
−
a
)
n
=
T
n
f
(
x
;
a
)
+
f
(
n
)
(
ξ
)
−
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle f(x)=T_{n-1}f(x;a)+{\frac {f^{(n)}(\xi )}{n!}}(x-a)^{n}=T_{n}f(x;a)+{\frac {f^{(n)}(\xi )-f^{(n)}(a)}{n!}}(x-a)^{n}}
Darum kann man als Restglied auch
R
n
f
(
x
;
a
)
=
f
(
n
)
(
ξ
)
−
f
(
n
)
(
a
)
n
!
(
x
−
a
)
n
{\displaystyle R_{n}f(x;a)={\frac {f^{(n)}(\xi )-f^{(n)}(a)}{n!}}(x-a)^{n}}
verwenden, wobei
f
{\displaystyle f}
n
{\displaystyle n}
Peano-Restglied .
Setzt man
Θ
=
ξ
−
a
x
−
a
{\displaystyle \Theta ={\tfrac {\xi -a}{x-a}}}
ξ
=
a
+
Θ
(
x
−
a
)
{\displaystyle \xi =a+\Theta (x-a)}
R
n
f
(
x
;
a
)
=
f
(
n
+
1
)
(
a
+
Θ
(
x
−
a
)
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
{\displaystyle R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{(n+1)!}}(x-a)^{n+1}}
die Schlömilchsche
R
n
f
(
x
;
a
)
=
f
(
n
+
1
)
(
a
+
Θ
(
x
−
a
)
)
p
⋅
n
!
(
1
−
Θ
)
n
+
1
−
p
(
x
−
a
)
n
+
1
{\displaystyle R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{p\cdot n!}}(1-\Theta )^{n+1-p}(x-a)^{n+1}}
und die Cauchysche
R
n
f
(
x
;
a
)
=
f
(
n
+
1
)
(
a
+
Θ
(
x
−
a
)
)
n
!
(
1
−
Θ
)
n
(
x
−
a
)
n
+
1
{\displaystyle R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{n!}}(1-\Theta )^{n}(x-a)^{n+1}}
jeweils für ein
Θ
{\displaystyle \Theta }
Liegt das Intervall
(
a
−
r
,
a
+
r
)
{\displaystyle (a-r,a+r)}
I
{\displaystyle I}
f
{\displaystyle f}
Restgliedformeln ) für alle
x
∈
(
a
−
r
,
a
+
r
)
{\displaystyle x\in (a-r,a+r)}
ξ
{\displaystyle \xi }
a
{\displaystyle a}
x
{\displaystyle x}
ξ
∈
(
a
−
r
,
a
+
r
)
{\displaystyle \xi \in (a-r,a+r)}
|
R
n
f
(
x
;
a
)
|
=
|
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
|
≤
sup
ξ
∈
(
a
−
r
,
a
+
r
)
|
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
a
)
n
+
1
|
{\displaystyle |R_{n}f(x;a)|=\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|\leq \sup _{\xi \in (a-r,a+r)}\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|}
Gilt
|
f
(
n
+
1
)
(
x
)
|
≤
M
n
{\displaystyle |f^{(n+1)}(x)|\leq M_{n}}
x
∈
(
a
−
r
,
a
+
r
)
{\displaystyle x\in (a-r,a+r)}
∀
x
∈
(
a
−
r
,
a
+
r
)
:
|
R
n
f
(
x
;
a
)
|
≤
M
n
|
x
−
a
|
n
+
1
(
n
+
1
)
!
≤
M
n
r
n
+
1
(
n
+
1
)
!
{\displaystyle \forall x\in (a-r,a+r):|R_{n}f(x;a)|\leq M_{n}{\frac {|x-a|^{n+1}}{(n+1)!}}\leq M_{n}{\frac {r^{n+1}}{(n+1)!}}}
Restgliedabschätzungen sind nicht auf den „reellen Fall“ beschränkt. Ist
D
⊆
K
{\displaystyle D\subseteq \mathbb {K} }
K
∈
{
R
,
C
}
{\displaystyle \mathbb {K} \in \{\mathbb {R} ,\mathbb {C} \}}
konvex (für
K
=
R
{\displaystyle \mathbb {K} =\mathbb {R} }
K
=
C
{\displaystyle \mathbb {K} =\mathbb {C} }
a
∈
D
{\displaystyle a\in D}
n
{\displaystyle n}
f
:
D
→
C
{\displaystyle f\colon D\to \mathbb {C} }
R
n
(
f
,
a
)
:
D
→
C
{\displaystyle R_{n}(f,a)\colon D\to \mathbb {C} }
[ 2]
f
(
x
)
=
∑
k
=
0
n
f
(
k
)
(
x
)
k
!
(
x
−
a
)
k
+
R
n
(
f
,
a
)
(
x
)
,
x
∈
D
.
{\displaystyle f(x)=\sum _{k=0}^{n}{\frac {f^{(k)}(x)}{k!}}(x-a)^{k}+R_{n}(f,a)(x),\qquad x\in D.}
Das Restglied genügt für
x
∈
D
{\displaystyle x\in D}
|
R
n
(
f
,
a
)
(
x
)
|
≤
|
x
−
a
|
n
(
n
−
1
)
!
sup
0
<
t
<
1
|
f
(
n
)
(
a
+
t
(
x
−
a
)
)
−
f
(
n
)
(
a
)
|
.
{\displaystyle |R_{n}(f,a)(x)|\leq {\frac {|x-a|^{n}}{(n-1)!}}\sup _{0<t<1}|f^{(n)}(a+t(x-a))-f^{(n)}(a)|.}
Eine Anwendung der Taylorformel sind Näherungsformeln, hier vorgestellt am Beispiel Sinus und Kosinus (wobei das Argument im Bogenmaß angegeben wird).
Für
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
f
′
(
x
)
=
cos
(
x
)
,
f
″
(
x
)
=
−
sin
(
x
)
,
f
‴
(
x
)
=
−
cos
(
x
)
,
f
⁗
(
x
)
=
sin
(
x
)
{\displaystyle f'(x)=\cos(x),\,f''(x)=-\sin(x),\,f'''(x)=-\cos(x),f''''(x)=\sin(x)}
T
4
sin
(
x
;
0
)
=
f
(
0
)
+
f
′
(
0
)
x
+
1
2
f
″
(
0
)
x
2
+
1
6
f
‴
(
0
)
x
3
+
1
24
f
⁗
(
0
)
x
4
=
x
−
x
3
6
.
{\displaystyle T_{4}\sin(x;0)=f(0)+f'(0)x+{\frac {1}{2}}f''(0)x^{2}+{\frac {1}{6}}f'''(0)x^{3}+{\frac {1}{24}}f''''(0)x^{4}=x-{\frac {x^{3}}{6}}.}
Aus
f
(
5
)
(
x
)
=
cos
(
x
)
{\displaystyle f^{(5)}(x)=\cos(x)}
R
4
sin
(
x
;
0
)
=
f
(
5
)
(
ξ
)
5
!
x
5
=
cos
(
ξ
)
120
x
5
{\displaystyle R_{4}\sin(x;0)={\frac {f^{(5)}(\xi )}{5!}}x^{5}={\frac {\cos(\xi )}{120}}x^{5}}
ξ
{\displaystyle \xi }
x
{\displaystyle x}
|
cos
(
ξ
)
|
≤
1
{\displaystyle |{\cos(\xi )}|\leq 1}
|
T
4
sin
(
x
;
0
)
−
sin
(
x
)
|
≤
|
x
|
5
120
{\displaystyle |T_{4}\sin(x;0)-\sin(x)|\leq {\frac {|x|^{5}}{120}}}
Liegt
x
{\displaystyle x}
−
π
4
{\displaystyle -{\frac {\pi }{4}}}
π
4
{\displaystyle {\frac {\pi }{4}}}
|
T
4
sin
(
x
;
0
)
−
sin
(
x
)
sin
(
x
)
|
{\displaystyle \left|{\frac {T_{4}\sin(x;0)-\sin(x)}{\sin(x)}}\right|}
T
3
sin
(
x
;
0
)
{\displaystyle T_{3}\sin(x;0)}
sin
(
x
)
{\displaystyle \sin(x)}
Tatsächlich genügt für die Annäherung des Sinus auf diese Genauigkeit sogar schon das Taylorpolynom 3. Ordnung, da
f
⁗
(
0
)
=
0
{\displaystyle f''''(0)=0}
f
(
x
)
=
sin
(
x
)
{\displaystyle f(x)=\sin(x)}
T
3
sin
(
x
;
0
)
=
T
4
sin
(
x
;
0
)
{\displaystyle T_{3}\sin(x;0)=T_{4}\sin(x;0)}
|
T
4
sin
(
x
;
0
)
−
sin
(
x
)
|
≤
x
4
24
{\displaystyle |T_{4}\sin(x;0)-\sin(x)|\leq {\frac {x^{4}}{24}}}
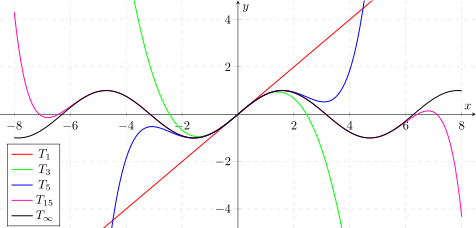
Die folgende Abbildung zeigt die Graphen einiger Taylorpolynome des Sinus um Entwicklungsstelle 0 für
n
=
1
,
3
,
5
,
15
{\displaystyle n=1,3,5,15}
n
=
∞
{\displaystyle n=\infty }
Taylorreihe , die mit der Sinusfunktion übereinstimmt.
Approximation des Sinus durch Taylorpolynome
T
1
sin
(
x
;
0
)
{\displaystyle T_{1}\sin(x;0)}
T
40
sin
(
x
;
0
)
{\displaystyle T_{40}\sin(x;0)}
Das vierte Taylorpolynom
T
4
cos
(
x
;
0
)
{\displaystyle T_{4}\cos(x;0)}
Horner-Schema diese Gestalt:
cos
(
x
)
≈
T
4
cos
(
x
;
0
)
=
(
x
2
12
−
1
)
⋅
x
2
2
+
1
{\displaystyle \cos(x)\approx T_{4}\cos(x;0)=\left({\frac {x^{2}}{12}}-1\right)\cdot {\frac {x^{2}}{2}}+1}
Liegt x zwischen
−
π
4
{\displaystyle -{\frac {\pi }{4}}}
π
4
{\displaystyle {\frac {\pi }{4}}}
|
T
4
cos
(
x
;
0
)
−
cos
(
x
)
cos
(
x
)
|
{\displaystyle \left|{\frac {T_{4}\cos(x;0)-\cos(x)}{\cos(x)}}\right|}
Auch für Kotangens und Tangens kann man diese Formeln nutzen, denn es ist
tan
(
x
)
∼
t
(
x
)
=
T
3
sin
(
x
;
0
)
T
4
cos
(
x
;
0
)
{\displaystyle \tan(x)\sim t(x)={\frac {T_{3}\sin(x;0)}{T_{4}\cos(x;0)}}}
mit einer relativen Abweichung von unter 0,5 % für
|
x
|
<
π
4
{\displaystyle \left|x\right|<{\frac {\pi }{4}}}
cot
(
x
)
∼
1
/
t
(
x
)
{\displaystyle \cot(x)\sim 1/t(x)}
t
{\displaystyle t}
Braucht man eine noch höhere Genauigkeit für seine Näherungsformeln, dann kann man auf höhere Taylorpolynome zurückgreifen, die die Funktionen noch besser approximieren.
Sei nun im Folgenden
f
:
R
d
→
R
{\displaystyle f\colon \mathbb {R} ^{d}\to \mathbb {R} }
n
+
1
{\displaystyle n+1}
x
=
(
x
1
,
…
,
x
d
)
,
a
=
(
a
1
,
…
,
a
d
)
∈
R
d
{\displaystyle x=(x_{1},\ldots ,x_{d}),a=(a_{1},\ldots ,a_{d})\in \mathbb {R} ^{d}}
F
:
R
→
R
{\displaystyle F\colon \mathbb {R} \to \mathbb {R} }
F
(
t
)
=
f
(
a
+
t
h
)
{\displaystyle F(t)=f(a+th)}
h
=
x
−
a
{\displaystyle h=x-a}
Sei ferner wie in der Multiindex-Notation
D
α
=
∂
|
α
|
∂
x
1
α
1
⋯
∂
x
d
α
d
{\displaystyle D^{\alpha }={\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{d}^{\alpha _{d}}}}}
Multiindex -Notation verwendet, damit man sofort sieht, dass der mehrdimensionale Fall für
d
=
1
{\displaystyle d=1}
Mit der mehrdimensionalen Kettenregel und Induktion erhält man, dass
F
(
n
)
(
t
)
=
∑
|
α
|
=
n
(
n
α
)
(
x
−
a
)
α
D
α
f
(
a
+
t
h
)
{\displaystyle F^{(n)}(t)=\sum _{|\alpha |=n}\left({\begin{matrix}n\\\alpha \end{matrix}}\right)(x-a)^{\alpha }D^{\alpha }f(a+th)}
wobei
(
n
α
)
{\displaystyle \left({\begin{matrix}n\\\alpha \end{matrix}}\right)}
Multinomialkoeffizient ist, siehe auch Multinomialtheorem .
Stellt man
F
{\displaystyle F}
f
{\displaystyle f}
a
{\displaystyle a}
T
n
f
(
x
;
a
)
:=
T
n
F
(
1
;
0
)
=
∑
|
α
|
=
0
n
(
x
−
a
)
α
α
!
D
α
f
(
a
)
{\displaystyle T_{n}f(x;a):=T_{n}F(1;0)=\sum _{|\alpha |=0}^{n}{\frac {(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a)}
Hierbei hat man verwendet, dass
(
n
α
)
⋅
1
n
!
=
1
α
!
{\displaystyle \left({\begin{matrix}n\\\alpha \end{matrix}}\right)\cdot {\frac {1}{n!}}={\frac {1}{\alpha !}}}
Das zweite Taylorpolynom einer skalarwertigen Funktion in mehr als einer Variable kann bis zur zweiten Ordnung kompakter geschrieben werden als:
T
2
f
(
x
;
a
)
=
f
(
a
)
+
∇
f
(
a
)
T
(
x
−
a
)
+
1
2
(
x
−
a
)
T
H
f
(
a
)
(
x
−
a
)
{\displaystyle T_{2}f(x;a)=f(a)+\nabla f(a)^{\mathrm {T} }(x-a)+{\frac {1}{2}}(x-a)^{\mathrm {T} }\operatorname {H} _{f}(a)(x-a)}
Dabei ist
∇
f
(
a
)
{\displaystyle \nabla f(a)}
Gradient und
H
f
(
a
)
{\displaystyle \operatorname {H} _{f}(a)}
Hesse-Matrix von
f
{\displaystyle f}
a
{\displaystyle a}
Das zweite Taylorpolynom nennt man auch Schmiegquadrik .
Ebenso definiert man das mehrdimensionale Restglied mithilfe der Multiindex -Notation:
R
n
f
(
x
;
a
)
:=
R
n
F
(
1
;
0
)
=
∫
0
1
(
1
−
t
)
n
n
!
F
(
n
+
1
)
(
t
)
d
t
=
(
n
+
1
)
∫
0
1
∑
|
α
|
=
n
+
1
(
1
−
t
)
n
(
x
−
a
)
α
α
!
D
α
f
(
a
+
t
h
)
d
t
{\displaystyle {\begin{aligned}R_{n}f(x;a):=&R_{n}F(1;0)=\int \limits _{0}^{1}{\frac {(1-t)^{n}}{n!}}F^{(n+1)}(t)\,\mathrm {d} t\\=&(n+1)\int \limits _{0}^{1}\sum _{|\alpha |=n+1}{\frac {(1-t)^{n}(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a+th)\,\mathrm {d} t\end{aligned}}}
Aus der eindimensionalen Taylor-Formel folgt, dass
F
(
1
)
=
T
n
F
(
1
;
0
)
+
R
n
F
(
1
;
0
)
{\displaystyle F(1)=T_{n}F(1;0)+R_{n}F(1;0)}
Nach der obigen Definition von
F
(
t
)
{\displaystyle F(t)}
f
(
x
)
=
T
n
f
(
x
;
a
)
+
R
n
f
(
x
;
a
)
{\displaystyle f(x)=T_{n}f(x;a)+R_{n}f(x;a)}
Man kann auch die eindimensionalen Nicht-Integral-Restgliedformeln mithilfe der Formel für
F
(
n
)
(
t
)
{\displaystyle F^{(n)}(t)}
Das Schlömilch-Restglied wird so zu
R
n
f
(
x
;
a
)
=
(
n
+
1
)
(
1
−
θ
)
n
+
1
−
p
p
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
+
θ
h
)
α
!
{\displaystyle R_{n}f(x;a)={\frac {(n+1)(1-\theta )^{n+1-p}}{p}}\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}}
das Lagrange-Restglied zu
R
n
f
(
x
;
a
)
=
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
+
θ
h
)
α
!
{\displaystyle R_{n}f(x;a)=\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}}
und das Cauchy-Restglied zu
R
n
f
(
x
;
a
)
=
(
n
+
1
)
(
1
−
θ
)
n
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
+
θ
h
)
α
!
{\displaystyle R_{n}f(x;a)=(n+1)(1-\theta )^{n}\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}}
für jeweils ein
θ
∈
[
0
,
1
]
{\displaystyle \theta \in [0,1]}
Nach der mehrdimensionalen Taylorformel ergibt sich mit dem Lagrange-Restglied:
f
(
x
)
−
T
n
+
1
f
(
x
;
a
)
=
(
n
+
1
)
(
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
+
θ
h
)
α
!
−
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
)
α
!
)
{\displaystyle f(x)-T_{n+1}f(x;a)=(n+1)\left(\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}-\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a)}{\alpha !}}\right)}
Wegen
|
x
i
−
a
i
|
≤
‖
x
−
a
‖
{\displaystyle |x_{i}-a_{i}|\leq \|x-a\|}
(
n
+
1
)
|
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
+
θ
h
)
α
!
−
∑
|
α
|
=
n
+
1
(
x
−
a
)
α
D
α
f
(
a
)
α
!
|
≤
(
n
+
1
)
‖
x
−
a
‖
n
+
1
⋅
|
∑
|
α
|
=
n
+
1
D
α
f
(
a
+
θ
h
)
−
D
α
f
(
a
)
α
!
|
⏟
→
0
,
x
→
a
{\displaystyle {\begin{aligned}&(n+1)\left|\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}-\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a)}{\alpha !}}\right|\\\leq &(n+1)\|x-a\|^{n+1}\cdot \underbrace {\left|\sum _{|\alpha |=n+1}{\frac {D^{\alpha }f(a+\theta h)-D^{\alpha }f(a)}{\alpha !}}\right|} _{\to 0{\text{, }}x\to a}\end{aligned}}}
Der letzte Teil geht gegen null, da die partiellen Ableitungen vom Grad
n
+
1
{\displaystyle n+1}
a
+
θ
h
{\displaystyle a+\theta h}
x
{\displaystyle x}
a
{\displaystyle a}
a
{\displaystyle a}
x
→
a
{\displaystyle x\to a}
Wir erhalten folgende Abschätzung, welche „(mehrdimensionale) qualitative Taylorformel“ genannt wird:
f
(
x
)
=
T
n
+
1
f
(
x
;
a
)
+
O
(
‖
x
−
a
‖
n
+
1
)
{\displaystyle f(x)=T_{n+1}f(x;a)+{\mathcal {O}}(\|x-a\|^{n+1})}
für
x
→
a
{\displaystyle x\to a}
O
{\displaystyle {\mathcal {O}}}
Landau-Notation steht.[ 3]
Es soll die Funktion
f
:
{
(
x
1
,
x
2
)
∈
R
2
,
x
2
<
1
}
→
R
,
(
x
1
,
x
2
)
↦
exp
(
x
1
−
x
2
)
⋅
log
(
1
−
x
2
)
{\displaystyle f:\{(x_{1},x_{2})\in \mathbb {R} ^{2},\ x_{2}<1\}\to \mathbb {R} ,~(x_{1},x_{2})\mapsto \exp(x_{1}-x_{2})\cdot \log(1-x_{2})}
um den Punkt
a
=
(
a
1
,
a
2
)
=
(
1
,
0
)
∈
R
2
{\displaystyle a=(a_{1},a_{2})=(1,0)\in \mathbb {R} ^{2}}
Funktion (rot) und Taylorentwicklung (grün) In diesem Beispiel soll die Funktion bis zum zweiten Grad entwickelt werden, d. h., man will ein Taylorpolynom zweiter Ordnung berechnen, also die sog. Schmiegquadrik . Es gilt also
n
=
2
{\displaystyle n=2}
|
α
|
≤
n
{\displaystyle |\alpha |\leq n}
Multiindexschreibweise , die Tupel
(
0
,
0
)
{\displaystyle (0,0)}
(
1
,
0
)
{\displaystyle (1,0)}
(
0
,
1
)
{\displaystyle (0,1)}
(
2
,
0
)
{\displaystyle (2,0)}
(
1
,
1
)
{\displaystyle (1,1)}
(
0
,
2
)
{\displaystyle (0,2)}
Satzes von Schwarz , dass
∂
2
f
∂
x
1
∂
x
2
(
a
)
=
∂
2
f
∂
x
2
∂
x
1
(
a
)
{\displaystyle {\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)={\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)}
Die partiellen Ableitungen der Funktion lauten:
∂
f
∂
x
1
(
a
)
=
[
exp
(
x
1
−
x
2
)
⋅
log
(
1
−
x
2
)
]
x
=
(
1
,
0
)
=
0
{\displaystyle {\frac {\partial f}{\partial x_{1}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0}
∂
f
∂
x
2
(
a
)
=
[
−
exp
(
x
1
−
x
2
)
⋅
(
log
(
1
−
x
2
)
+
1
1
−
x
2
)
]
x
=
(
1
,
0
)
=
−
e
{\displaystyle {\frac {\partial f}{\partial x_{2}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e}
∂
2
f
∂
x
1
2
(
a
)
=
[
exp
(
x
1
−
x
2
)
⋅
log
(
1
−
x
2
)
]
x
=
(
1
,
0
)
=
0
{\displaystyle {\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0}
∂
2
f
∂
x
1
∂
x
2
(
a
)
=
∂
2
f
∂
x
2
∂
x
1
(
a
)
=
[
−
exp
(
x
1
−
x
2
)
⋅
(
log
(
1
−
x
2
)
+
1
1
−
x
2
)
]
x
=
(
1
,
0
)
=
−
e
{\displaystyle {\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)={\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e}
∂
2
f
∂
x
2
2
(
a
)
=
[
exp
(
x
1
−
x
2
)
(
log
(
1
−
x
2
)
+
2
1
−
x
2
−
1
(
1
−
x
2
)
2
)
]
x
=
(
1
,
0
)
=
e
{\displaystyle {\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\left(\log(1-x_{2})+{\frac {2}{1-x_{2}}}-{\frac {1}{(1-x_{2})^{2}}}\right)\right]_{x=(1,0)}=e}
Es folgt mit der mehrdimensionalen Taylor-Formel:
f
(
x
)
≈
f
(
a
)
+
1
1
!
∂
f
∂
x
1
(
a
)
(
x
1
−
a
1
)
+
1
1
!
∂
f
∂
x
2
(
a
)
(
x
2
−
a
2
)
+
1
2
!
∂
2
f
∂
x
1
2
(
a
)
(
x
1
−
a
1
)
2
+
1
1
!
1
!
∂
2
f
∂
x
1
∂
x
2
(
a
)
(
x
1
−
a
1
)
(
x
2
−
a
2
)
+
1
2
!
∂
2
f
∂
x
2
2
(
a
)
(
x
2
−
a
2
)
2
=
0
+
0
−
e
(
x
2
−
0
)
+
0
−
e
(
x
1
−
1
)
(
x
2
−
0
)
+
1
2
e
(
x
2
−
0
)
2
=
−
e
x
1
x
2
+
1
2
e
x
2
2
{\displaystyle {\begin{aligned}f(x)\approx &f(a)+{\frac {1}{1!}}{\frac {\partial f}{\partial x_{1}}}(a)~(x_{1}-a_{1})+{\frac {1}{1!}}{\frac {\partial f}{\partial x_{2}}}(a)~(x_{2}-a_{2})\\&+{\frac {1}{2!}}{\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)~(x_{1}-a_{1})^{2}+{\frac {1}{1!1!}}{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)~(x_{1}-a_{1})(x_{2}-a_{2})\\&+{\frac {1}{2!}}{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)~(x_{2}-a_{2})^{2}\\&=0+0-e(x_{2}-0)+0-e(x_{1}-1)(x_{2}-0)+{\frac {1}{2}}e(x_{2}-0)^{2}\\&=-ex_{1}x_{2}+{\frac {1}{2}}ex_{2}^{2}\end{aligned}}}
Benutzt man die alternative Darstellung mit Hilfe des Gradienten und der Hesse-Matrix, so erhält man:
f
(
x
)
≈
f
(
a
)
+
∇
f
(
a
)
T
(
x
−
a
)
+
1
2
(
x
−
a
)
T
H
f
(
a
)
(
x
−
a
)
=
f
(
a
)
+
(
∂
f
∂
x
1
(
a
)
∂
f
∂
x
2
(
a
)
)
(
x
1
−
a
1
x
2
−
a
2
)
+
1
2
(
x
1
−
a
1
x
2
−
a
2
)
(
∂
2
f
∂
x
1
2
(
a
)
∂
2
f
∂
x
2
∂
x
1
(
a
)
∂
2
f
∂
x
1
∂
x
2
(
a
)
∂
2
f
∂
x
2
2
(
a
)
)
(
x
1
−
a
1
x
2
−
a
2
)
=
0
+
(
0
−
e
)
(
x
1
−
1
x
2
)
+
1
2
(
x
1
−
1
x
2
)
(
0
−
e
−
e
e
)
(
x
1
−
1
x
2
)
=
−
e
x
1
x
2
+
1
2
e
x
2
2
{\displaystyle {\begin{aligned}f(x)&\approx f(a)+\nabla f(a)^{T}(x-a)+{\frac {1}{2}}(x-a)^{T}H_{f}(a)(x-a)\\&=f(a)+{\begin{pmatrix}{\frac {\partial f}{\partial x_{1}}}(a)&{\frac {\partial f}{\partial x_{2}}}(a)\end{pmatrix}}{\begin{pmatrix}x_{1}-a_{1}\\x_{2}-a_{2}\end{pmatrix}}\\&\qquad +{\frac {1}{2}}{\begin{pmatrix}x_{1}-a_{1}&x_{2}-a_{2}\end{pmatrix}}{\begin{pmatrix}{\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)&{\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)\\{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)&{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)\end{pmatrix}}{\begin{pmatrix}x_{1}-a_{1}\\x_{2}-a_{2}\end{pmatrix}}\\&=0+{\begin{pmatrix}0&-e\end{pmatrix}}{\begin{pmatrix}x_{1}-1\\x_{2}\end{pmatrix}}+{\frac {1}{2}}{\begin{pmatrix}x_{1}-1&x_{2}\end{pmatrix}}{\begin{pmatrix}0&-e\\-e&e\end{pmatrix}}{\begin{pmatrix}x_{1}-1\\x_{2}\end{pmatrix}}\\&=-ex_{1}x_{2}+{\frac {1}{2}}ex_{2}^{2}\end{aligned}}}
Mit überraschend wenig Aufwand lässt sich die Taylor-Formel noch weiter verallgemeinern: Seien
X
,
Y
,
{\displaystyle X,Y,}
Banachräume ,
U
⊆
X
{\displaystyle U\subseteq X}
offen und nichtleer. Weiter sei
f
:
U
→
Y
{\displaystyle f:U\rightarrow Y}
(
k
+
1
)
{\displaystyle (k+1)}
Fréchet-differenzierbarer Operator, sowie
a
∈
U
,
h
∈
X
{\displaystyle a\in U,h\in X}
a
+
t
h
∈
U
{\displaystyle a+th\in U}
t
∈
[
0
,
1
]
{\displaystyle t\in [0,1]}
f
(
a
+
h
)
=
f
(
a
)
+
∑
j
=
1
k
1
j
!
D
j
f
(
a
)
(
h
,
.
.
.
,
h
)
+
R
k
+
1
(
a
,
h
)
{\displaystyle f(a+h)=f(a)+\sum \limits _{j=1}^{k}{\frac {1}{j!}}D^{j}f(a)(h,...,h)+R_{k+1}(a,h)}
Hierbei ist
D
j
f
(
a
)
{\displaystyle D^{j}f(a)}
j
{\displaystyle j}
f
{\displaystyle f}
j
{\displaystyle j}
X
{\displaystyle X}
Y
{\displaystyle Y}
R
k
+
1
{\displaystyle R_{k+1}}
Dualraumes
T
∈
X
∗
{\displaystyle T\in X^{*}}
T
R
k
+
1
(
a
,
h
)
=
∫
0
1
(
1
−
t
)
k
k
!
T
D
k
+
1
f
(
a
+
t
h
)
(
h
,
.
.
.
,
h
)
d
t
{\displaystyle TR_{k+1}(a,h)=\int \limits _{0}^{1}{\frac {(1-t)^{k}}{k!}}TD^{k+1}f(a+th)(h,...,h)dt}
Beweis:
Sei
T
∈
Y
∗
{\displaystyle T\in Y^{*}}
γ
:
[
0
,
1
]
→
R
,
t
↦
T
f
(
a
+
t
h
)
{\displaystyle \gamma :[0,1]\rightarrow \mathbb {R} ,t\mapsto Tf(a+th)}
(
k
+
1
)
{\displaystyle (k+1)}
γ
(
1
)
=
γ
(
0
)
+
∑
j
=
1
k
γ
j
(
0
)
j
!
(
1
−
0
)
+
∫
0
1
(
1
−
t
)
k
k
!
D
k
+
1
γ
(
t
)
d
t
.
{\displaystyle \gamma (1)=\gamma (0)+\sum \limits _{j=1}^{k}{\frac {\gamma ^{j}(0)}{j!}}(1-0)+\int \limits _{0}^{1}{\frac {(1-t)^{k}}{k!}}D^{k+1}\gamma (t)dt.}
Mit Hilfe der Kettenregel für die Fréchet-Ableitung folgt hieraus die gewünschte Formel für
T
f
{\displaystyle Tf}
Satzes von Hahn-Banach die entsprechende Formel für
f
{\displaystyle f}
Otto Forster : Analysis. Band 1: Differential- und Integralrechnung einer Veränderlichen. 8., verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0088-0 (Vieweg Studium. Grundkurs Mathematik ).Otto Forster: Analysis. Band 2: Differentialrechnung im R n Gewöhnliche Differentialgleichungen. 7., verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0250-6 (Vieweg Studium. Grundkurs Mathematik ).
Bernhard Heck : Rechenverfahren und Auswertemodelle der Landesvermessung. Klassische und moderne Methoden. Wichmann, Karlsruhe 1987, ISBN 3-87907-173-X , Kapitel 4, 7 und 13 (Mathematische Modelle und Grundlagen).Konrad Königsberger : Analysis. Band 2. 3., überarbeitete Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-66902-7 .
↑ Brook Taylor: Methodus Incrementorum Directa et Inversa. Pearson, London 1717, S. 21 .
↑ Herbert Amann, Joachim Escher: Analysis 1 . Dritte Auflage. Birkhäuser, S. 354.
↑ Königsberger: Analysis. Band 2. 2000, S. 66.














































![{\displaystyle {\begin{aligned}&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+R_{n+1}f(x;a)\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\int \limits _{a}^{x}{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+2)}(t)\,\mathrm {d} t\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\left[{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+1)}(t)\right]_{t=a}^{t=x}-\int \limits _{a}^{x}{\frac {-(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t\\=&{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)-{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)+R_{n}f(x;a)\\=&R_{n}f(x;a)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc95cc12360fa9829b2cb47b06fb938625435f4)




















































































![{\displaystyle \theta \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)


















![{\displaystyle {\frac {\partial f}{\partial x_{1}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80a34287647244879f4bda63a4390809aa833d72)
![{\displaystyle {\frac {\partial f}{\partial x_{2}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55df47c8d0210eccaca74dfbca03dc43fca5b193)
![{\displaystyle {\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5198d1f21234848dbe1c5d6be6e181b9a802a337)
![{\displaystyle {\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)={\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0a0aacab491129d05df9cc391f1ebb60c3f8273)
![{\displaystyle {\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\left(\log(1-x_{2})+{\frac {2}{1-x_{2}}}-{\frac {1}{(1-x_{2})^{2}}}\right)\right]_{x=(1,0)}=e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3366467863d74db9df78415e6feb044861bc6964)








![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)









![{\displaystyle \gamma :[0,1]\rightarrow \mathbb {R} ,t\mapsto Tf(a+th)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef2c82990ba9a89d4650f795dba1092295ec730)

