Feynman-Diagramm
Feynman-Diagramme sind in der Teilchen- und Festkörperphysik standardmäßig verwendete bildliche Darstellungen quantenfeldtheoretischer Wechselwirkungen, die 1949 von Richard Feynman am Beispiel der Quantenelektrodynamik entwickelt wurden.[1] Die Diagramme sind streng in mathematische Ausdrücke übersetzbar.
Bedeutung und Anwendung[Bearbeiten | Quelltext bearbeiten]
Feynman-Diagramme sind eine abstrakte, graphische Repräsentation der Wechselwirkungen von Teilchen, die mathematisch durch Lagrange-Dichten beschrieben werden. Beispielsweise wird die Interaktion zwischen Elektronen und Photonen durch die folgende Lagrange-Dichte beschrieben:
Hierbei ist der dem Elektron (oder Positron) entsprechende Dirac-Spinor, das dazu komplex-konjugierte und transponierte Feld, die elektrische Ladung, die Masse des Elektrons, die Dirac-Matrizen und das dem Photon entsprechende elektromagnetische Viererpotential. Die Ableitung beschreibt die Ausbreitung des Elektrons in der Raumzeit, während der Ausdruck die elektrische Ladung des Elektrons mit dem Photon koppelt. Die Indizes und stellen die vier Dimensionen des Minkowski-Raums ( für die Koordinaten ) dar. Es gilt die Einsteinsche Summenkonvention, und die Einheiten sind so gewählt, dass gilt.

Solche Ausdrücke sind im Allgemeinen sehr kompliziert, lassen sich jedoch eindeutig in entsprechende Feynman-Diagramme übersetzen, die eine vereinfachte und anschauliche Darstellung bieten. Eine einfache Berechnung der mathematischen Ausdrücke erlauben Feynman-Diagramme jedoch nicht. Hierzu muss auf die mathematischen Formeln zurückgegriffen werden.
Üblicherweise werden Feynman-Diagramme dazu verwendet, die Berechnung von Streuprozessen in relativistischen Quantenfeldtheorien, z. B. in der Quantenelektrodynamik oder der Quantenchromodynamik, zu organisieren. Hierzu lässt sich die Gesamtamplitude eines Streuvorgangs als Summe aller gültigen Feynman-Diagramme in einer nach der Kopplungskonstanten entwickelten Potenzreihe aufschlüsseln. Anschließend können die einzelnen beitragenden Amplituden berechnet werden.
Zudem werden Feynman-Diagramme in der nichtrelativistischen Festkörperphysik, speziell in der Vielteilchenphysik und der Statistischen Physik, benutzt.[2]
Aufbau[Bearbeiten | Quelltext bearbeiten]
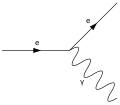
Feynman-Diagramme setzen sich aus grundlegenden Symbolen zusammen, die jeweils bestimmte Arten von Elementarteilchen abbilden. Fermionen (Materieteilchen) werden nach der üblichen Konvention mittels durchgezogener Linien mit Pfeil repräsentiert. Häufig wird das Antiteilchen als ein sich gegen die Zeit bewegendes Teilchen bezeichnet. Die Pfeilrichtung zeigt daher an, ob es sich um ein Teilchen (in Zeitrichtung) oder ein Antiteilchen (gegen die Zeitrichtung) handelt. Für die Beschriftung der Linien der Teilchen und Antiteilchen gibt es verschiedene Konventionen. Meist wird das genaue Symbol des Teilchens geschrieben. Manche Autoren verwenden aber eine kürzere und allgemeinere Schreibweise, die sowohl das Teilchen als auch das Antiteilchen bezeichnen kann (z. B. anstelle von und ), da die Information, ob es sich um ein Teilchen oder ein Antiteilchen handelt, bereits in der Pfeilrichtung steckt. Die Richtung der Zeitachse wird manchmal von unten nach oben, manchmal von links nach rechts gewählt.
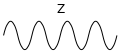
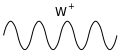
Die Eichbosonen, welche die Interaktion von Teilchen vermitteln, werden je nach Wechselwirkung üblicherweise durch wellen- oder spiralförmige Linien repräsentiert, skalare Teilchen typischerweise durch gestrichelte Linien. Abweichungen von diesen Konventionen kommen vor, beispielsweise können W-Bosonen als gestrichelte Linien symbolisiert werden.
Die Zeit wird im Folgenden von links nach rechts dargestellt.
| Symbol | Bedeutung |
|---|---|
| Fermion | |
| Antifermion | |
| Eichbosonen der elektroschwachen Wechselwirkung | |
| Gluon g (Eichboson der starken Wechselwirkung) | |
| Higgs-Boson (oder allgemein skalare Bosonen, seltener auch für Vektorbosonen) | |
| Terminator (z. B. Interaktion des Higgs-Bosons mit einem Kondensat[3]) |
Zusätzlich können Beschriftungen verwendet werden, um zu definieren, welches Elementarteilchen gemeint ist.
|
|
Feynman-Diagramme haben äußere Linien, die in Wechselwirkungspunkte ein- oder auslaufen, und innere Linien, die Paare von Wechselwirkungspunkten verbinden. Den äußeren Linien entsprechen ein- und auslaufende Teilchen. Die Wechselwirkungspunkte, an denen die Linien zusammentreffen, heißen auch Vertices. An einem Vertex können Teilchen erzeugt, vernichtet oder gestreut werden.
Unter Festhalten der Zeit (von links nach rechts verlaufend) führt die Drehung um einen Vertex zu unterschiedlichen Interpretationen:
- Konfluenz- und Splitting-Prozesse
-
Annihilation eines Elektrons und Positrons zu einem Photon
-
Emission eines Photons durch ein Elektron
-
Absorption eines Photons durch ein Positron
-
Paarbildung eines Elektrons und Positrons durch ein Photon
Hierbei gilt zu beachten, dass ein Feynman-Diagramm nur aus über Teilchen zusammenhängenden Vertices besteht.
Propagatoren[Bearbeiten | Quelltext bearbeiten]
Die inneren Linien nennt man Propagatoren und deutet sie als virtuelle Teilchen. Virtuelle Teilchen können nicht beobachtet werden. Aufgrund dessen ergibt sich eine Mehrdeutigkeit. Alle Diagramme mit den gleichen ein- und auslaufenden Linien sind äquivalent und werden summiert.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Bhabha-Streuung
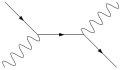
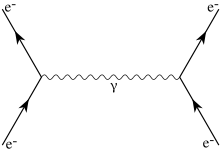
Zur Berechnung der Streuung eines Fermions und Antifermions – der Bhabha-Streuung – betrachtet man Feynman-Diagramme mit einem einlaufenden und einem auslaufenden Elektron-Positron-Paar.
Die Bilder zeigen die Streuung in niedrigster Ordnung (tree-level). Die vier äußeren Linien stehen für die ein- und auslaufenden Elektronen und Positronen, die innere Wellenlinie für das virtuelle Photon, das die elektromagnetische Wechselwirkung bewirkt.
-
Ein Fermion und Antifermion (z. B. Elektron und Positron) mit einem vermittelnden virtuellen Eichboson (z. B. Photon)
-
Ein äquivalentes Diagramm zur Bhabha-Streuung mit einem anderen Propagator.
Jedem dieser Diagramme entspricht ein Beitrag zur Streuung, der gesamte Streuvorgang wird durch die Summe aller Diagramme dargestellt.
Compton-Effekt
Als weiteres Beispiel sei hier der Compton-Effekt in der niedrigsten Ordnung aufgeführt. Auch hier werden die möglichen Diagramme summiert.
| Compton-Effekt = |
|
+ |
|
Die Berechnung dieser Streuung und allgemeiner die Feynman-Regeln für die mathematischen Ausdrücke, die den Linien und Vertices entsprechen, finden sich in vielen Lehrbüchern der Teilchenphysik (siehe Weblinks).
Schleifen[Bearbeiten | Quelltext bearbeiten]
Neben den tree-level-Diagrammen, benannt nach ihrer baumartigen Struktur, sind zur exakten Berechnung auch die Loop-Diagramme höherer Ordnung von Bedeutung.
-
keine Schleife
(tree-level) -
eine Schleife
(1-loop) -
zwei Schleifen
(2-loop) -
zwei Schleifen
(2-loop)
Die möglichen Feynman-Diagramme lassen sich nach der Zahl der inneren Schleifen ordnen, die als Loop-Ordnung bezeichnet wird, und im Zuge einer Reihenentwicklung aufsummieren:
- .
Es sind dabei beliebig viele Diagramme denkbar. Jedoch sind Beiträge höherer Ordnung mit der entsprechenden Potenz der Kopplungskonstanten unterdrückt. Mit ausreichend hoher Ordnung werden die Beiträge dann gemäß der Arbeitshypothese der Störungstheorie numerisch vernachlässigbar, da sie sich kaum auf das Ergebnis auswirken.
Feynman-Regeln[Bearbeiten | Quelltext bearbeiten]
Die Feynman-Regeln beschreiben, welche Wechselwirkungen möglich sind und welche nicht.
Photonen[Bearbeiten | Quelltext bearbeiten]
Photonen wechselwirken mit allen elektrisch geladenen Elementarteilchen. Abbildungen für Elektronen und Myonen:
-
Wechselwirkung zwischen Elektron, Positron und Photon
-
Wechselwirkung zwischen Myonen und Photon
Z-Bosonen[Bearbeiten | Quelltext bearbeiten]
Das Z-Boson wechselwirkt zwischen allen anderen Elementarteilchen des Standardmodells außer Gluonen, mit Photonen allerdings nur zugleich mit W-Bosonen. Insbesondere Neutrinos (, und ) wechselwirken nicht mit Photonen; daher ist man für deren Erzeugung und Nachweis auf Z-Bosonen und W-Bosonen angewiesen.
-
Wechselwirkung zwischen Z-Boson und Neutrinos
-
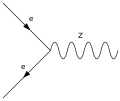
Wechselwirkung zwischen Elektron, Positron und Z-Boson
-
Wechselwirkung zwischen Myon, Anti-Myon und Z-Boson
W-Bosonen[Bearbeiten | Quelltext bearbeiten]
Das W-Boson vermittelt einerseits zwischen Neutrinos und den geladenen Leptonen l (Elektronen, Myonen und Tauonen) und andererseits zwischen Up-Typ-Quarks und Down-Typ-Quarks. Das W-Boson ist dabei der Träger einer positiven (W+) oder negativen (W−) elektrischen Ladung. Aufgrund der elektrischen Ladung unterliegt das W-Boson der Wechselwirkung mit dem Photon; außerdem wechselwirkt es mit dem Z-Boson sowie anderen W-Bosonen.
-
Wechselwirkung zwischen negativ geladenem Lepton, Neutrino und W-Boson
-
Wechselwirkung zwischen Neutrino, positiv geladenem Lepton und W-Boson
-
Wechselwirkung zwischen zwei unterschiedlich geladenen W-Bosonen. Zeitachse läuft von oben nach unten
-
Wechselwirkung zwischen zwei unterschiedlich geladenen W-Bosonen und zwei Photonen. Zeitachse läuft von oben nach unten
-
Wechselwirkung zwischen zwei unterschiedlich geladenen W-Bosonen und zwei Z-Bosonen. Zeitachse läuft von oben nach unten
-
Wechselwirkung zwischen zwei unterschiedlich geladenen W-Bosonen, einem Z-Boson und einem Photon. Zeitachse läuft von oben nach unten
W-Bosonen sind vor allem deshalb interessant, da sie einen Wechsel des Flavour erlauben. Das bedeutet, dass sich die Anzahl der Elektronen, Neutrinos etc. verändern kann. Diese Eigenschaft spielt etwa im β-Zerfall eine wichtige Rolle.
 |
 |
Gluonen[Bearbeiten | Quelltext bearbeiten]

Gluonen vermitteln die starke Wechselwirkung zwischen Quarks.
Quarks besitzen eine Farbladung. Im Gegensatz zur elektrischen Ladung, die „positiv“ (+) oder „negativ“ (-) sein kann, sind die möglichen Farbladungen „Rot“, „Grün“ und „Blau“ sowie als Antifarbladung „Anti-Rot“ („Cyan“), „Anti-Grün“ („Magenta“) und „Anti-Blau“ („Gelb“). Um die Farbladung zu neutralisieren, müssen wahlweise Quarks mit den Farbladungen {Rot,Grün,Blau}, {Cyan,Magenta,Gelb}, {Rot,Cyan}, {Grün,Magenta} oder {Blau,Gelb} über Gluonen verbunden werden.
Gluonen tragen jeweils eine Farbladung und eine Antifarbladung. Dadurch unterliegen sie selbst der starken Wechselwirkung und können sich somit untereinander verbinden. Theoretisch lassen sich so auch Gluon-Bälle erzeugen, welche nur aus Gluonen bestehen und ohne Quarks „auskommen“. Sie konnten jedoch bisher (2019) nicht nachgewiesen werden.
Higgs-Bosonen[Bearbeiten | Quelltext bearbeiten]
Das Higgs-Boson wechselwirkt mit allen massiven Elementarteilchen, also auch mit sich selbst (Selbstwechselwirkung). Lediglich mit Photonen und Gluonen gibt es keine Wechselwirkung. Nach dem Standardmodell der Teilchenphysik erhalten Elementarteilchen erst durch diese Wechselwirkung ihre Masse (siehe Higgs-Mechanismus).
Typen von Feynman-Diagrammen[Bearbeiten | Quelltext bearbeiten]
- Zusammenhängende Diagramme
- Ist jeder Vertex über innere Linien und andere Vertices mit jedem anderen Vertex verbunden, so bezeichnet man das Diagramm als zusammenhängend, anderenfalls als unzusammenhängend. Bei jedem zusammenhängenden Teil des Diagramms ist die Summe der Energien, Impulse und Ladungen der einlaufenden Teilchen gleich der Summe der Energien, Impulse und Ladungen der auslaufenden Teilchen.
- Ein-Teilchen-irreduzible Diagramme
- Kann ein zusammenhängendes Diagramm nicht durch Zerschneiden einer inneren Linie in zwei unzusammenhängende Diagramme geteilt werden, so heißt es Ein-Teilchen-irreduzibel. Bei solchen Diagrammen treten Integrationen auf, die man nicht systematisch als Produkt einfacherer Integrale vereinfachen kann.
- Amputierte Diagramme
- Lässt man bei einem Diagramm Korrekturen (Selbstenergien, s. u.) zu den äußeren Linien weg, so bezeichnet man es als amputiert.
- Selbstenergie-Diagramme
- Ein Diagramm mit einem Loop und mit äußeren Linien an nur zwei Vertices heißt (nach Amputation) Selbstenergiediagramm. Sein Wert hängt nur von der Energie und dem Impuls ab, der durch äußere Linien an dem einen Vertex hinein- und an dem anderen hinaus fließt.
- Skelett-Diagramme
- Ein Diagramm ohne ein Selbstenergie-Unterdiagramm bezeichnet man als Skelett-Diagramm.
Festkörperphysikalische Analogie[Bearbeiten | Quelltext bearbeiten]
Die gebräuchliche Übertragung auf die Festkörperphysik erhält man, indem man von der geschweift dargestellten Photonlinie, also von den Quanten der elektromagnetischen Wellen, zu den sog. Phononen übergeht, also zu den Schallquanten, und indem man das rückwärts laufende Elektron nicht als Positron im Sinne der Quantenelektrodynamik, sondern als Defektelektron im Sinne der Festköpertheorie interpretiert. Man erhält auf diese Weise u. a. die wesentlichen Diagramme für das Zustandekommen der Supraleitung und allgemein für Konfluenz- und Splitting-Prozesse durch Vernichtung bzw. Erzeugung einer elementaren fermionischen Anregung (z. B. eines (negativ geladenen) Elektrons bzw. eines (positiv geladenen) Defektelektrons bzw. eines Polarons) zusammen mit einem einlaufenden (oder auslaufenden) bosonischen Quasiteilchens, z. B. des schon erwähnten Phonons oder eines sog. Magnons (quantisierte Spinwellen) oder eines Plasmons (einer quantisierten Plasmaschwingung).
Bei allen Wechselwirkungsprozessen unter Beteiligung der erwähnten Anregungen ist die Summe der Energien (Frequenzen mal ) bzw. der Impulse (Wellenzahlen mal ) erhalten, sodass also den dargestellten Diagrammen wohldefinierte mathematische Ausdrücke für die Amplituden der Wechselwirkung entsprechen.
Umsetzung in der Kunst[Bearbeiten | Quelltext bearbeiten]

Die Feynman-Graphen haben auch Eingang in die zeitgenössische Kunst gefunden. Der deutsche Glaskünstler Karl-Martin Hartmann schuf im Jahr 2000 für die Kirche St. Nicolai in Kalkar ein Chorfenster, das er aus einem Raster aus Feynman-Graphen gestaltete. Physikalische Erkenntnisse und die Schönheit der Naturwissenschaften sollen in diesem sakralen Kontext in einen Dialog mit den Lehren und Botschaften der Religion treten.[4]
Literatur[Bearbeiten | Quelltext bearbeiten]
Moderne Werke[Bearbeiten | Quelltext bearbeiten]
- Stefan Weinzierl: Feynman Integrals: A Comprehensive Treatment for Students and Researchers (= UNITEXT for Physics). Springer International Publishing, Cham 2022, ISBN 978-3-03099557-7, doi:10.1007/978-3-030-99558-4 (englisch).
Ältere Werke[Bearbeiten | Quelltext bearbeiten]
- David J. Griffiths: Introduction to Elementary Particles (= Physics textbook). 2. Auflage. Wiley-VCH, Weinheim 2008, ISBN 978-3-527-40601-2 (englisch, archive.org).
- Richard D. Mattuck: A Guide to Feynman Diagrams in the Many-Body Problem (= Dover books on physics and chemistry). 2. Auflage. Dover Publications, New York 1992, ISBN 978-0-486-67047-8 (englisch, archive.org [abgerufen am 12. Januar 2024]).
- Peter Schmüser: Feynman-Graphen und Eichtheorien für Experimentalphysiker. Springer Berlin Heidelberg, Berlin, Heidelberg 1995, ISBN 978-3-540-58486-5, doi:10.1007/978-3-642-57766-6.
Originalarbeiten[Bearbeiten | Quelltext bearbeiten]
Hinweis: Es handelt sich um nachgebesserte, verfügbare Originalarbeiten.
- Richard P. Feynman: Feynman’s Thesis – A New Approach to Quantum Theory. Hrsg.: Laurie M. Brown. World Scientific, Hackensack, NJ 2005, ISBN 978-981-256-366-8 (englisch).
- Richard P. Feynman, Albert R. Hibbs, Daniel F. Styer: Quantum Mechanics and Path Integrals. Emended edition Auflage. Dover Publications, Mineola, NY 2010, ISBN 978-0-486-47722-0 (englisch).
Historie[Bearbeiten | Quelltext bearbeiten]
- Als Präsentation von Prof. David Kaiser: Lecture 21: Teaching Feynman's Tools: The Dispersion of Feynman Diagrams in Postwar Physics. MIT, Oktober 2020, abgerufen am 12. Januar 2024 (englisch).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Wie funktionieren Feynman-Diagramme? In: ScienceBlogs. Konradin Medien, 9. Oktober 2010, abgerufen am 12. Januar 2024.
- Plip Tanedo: Let’s draw Feynman diagrams! In: Quantum Diaries. USLHC, Cornell University, 14. Februar 2010, abgerufen am 12. Januar 2024 (englisch).
- Carl Brannen: Feynman Diagrams for the Masses (part 1). Abgerufen am 12. Januar 2024 (englisch).
- Carl Brannen: Feynman Diagrams for the Masses (part 2). Abgerufen am 12. Januar 2024 (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ R. P. Feynman: Space-Time Approach to Quantum Electrodynamics. In: Physical Review. Band 76, Nr. 6, 15. September 1949, ISSN 0031-899X, S. 769–789, doi:10.1103/PhysRev.76.769 (caltech.edu [PDF; abgerufen am 11. Februar 2023]).
- ↑ Abrikosov, Gor'kov, Dzyaloshinskii: Quantum field theory methods in statistical physics. Dover, 1961 und 1977, ISBN 0-486-63228-8.
- ↑ Demystifying the Higgs Boson with Leonard Susskind. In: YouTube. Stanford University, 16. August 2012, abgerufen am 27. Februar 2013 (englisch).
- ↑ www.pro-physik.de/details/articlePdf/1106933/issue.html (Memento vom 20. Juni 2016 im Internet Archive) Physik sakral: Interview mit dem Künstler im Physik Journal 3 (2004) Nr. 12, abgerufen am 14. Januar 2019