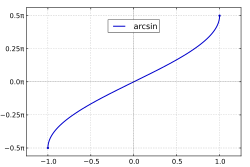
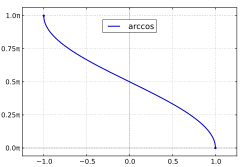
Arkussinus und Arkuskosinus

Arkussinus und Arkus­kosinus im kartesi­schen Koordinaten­system

arcsin (x)

arccos (x)

Der Arkussinus – geschrieben $\arcsin$ oder $\operatorname {asin}$ – und der Arkuskosinus (oder auch Arkuscosinus) – geschrieben $\arccos$ oder $\operatorname {acos}$ – sind Umkehrfunktionen der (geeignet) eingeschränkten Sinus- bzw. Kosinusfunktion. Sinus und Kosinus sind Funktionen, die einen Winkel auf einen Wert im Intervall $[-1,1]$ abbilden; als deren Umkehrfunktionen bilden Arkussinus und Arkuskosinus einen Wert aus $[-1,1]$ wieder auf einen zugehörigen Winkel ab. Da Sinus und Kosinus periodische Funktionen sind, gibt es aber zu jedem Wert aus $[-1,1]$ unendlich viele zugehörige Winkel. Daher wird zur Umkehrung von Sinus und Kosinus deren Definitionsmenge auf das Intervall $[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}]$ für Sinus und auf $[0,\pi ]$ für Kosinus eingeschränkt. Sinus und Kosinus sind auf diesen Intervallen streng monoton und daher umkehrbar.

Zusammen mit dem Arkustangens als Umkehrfunktion des (natürlich ebenfalls geeignet eingeschränkten) Tangens bilden der Arkussinus und Arkuskosinus den Kern der Klasse der Arkusfunktionen. Aufgrund der in neuerer Zeit für Umkehrfunktionen gebräuchlichen Schreibweise $f^{-1}$ beginnen die namentlich auf Taschenrechnern verbreiteten Schreibweisen $\sin ^{-1}$ und $\cos ^{-1}$ die klassische Schreibweise $\arcsin$ bzw. $\arccos$ zu verdrängen, was eventuell zu Verwechslungen mit den Kehrwerten des Sinus und Kosinus (Kosekans und Sekans) führen kann.

Definitionen

Die Sinusfunktion ist $2\pi$-periodisch und innerhalb einer Periode nicht injektiv. Daher muss ihr Definitionsbereich geeignet eingeschränkt werden, um eine umkehrbar-eindeutige Funktion zu erhalten. Da es für diese Einschränkung mehrere Möglichkeiten gibt, spricht man von Zweigen des Arkussinus. Meist wird der Hauptzweig (oder Hauptwert)

$\arcsin \colon [-1,1]\to \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],$

die Umkehrfunktion der Einschränkung $\sin |_{\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$ der Sinusfunktion auf das Intervall $\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],$ betrachtet.

Analog zum Arkussinus wird der Hauptzweig des Arkuskosinus als die Umkehrfunktion von $\cos |_{[0,\pi ]}$ definiert. Dies ergibt mit

$\arccos \colon [-1,1]\to [0,\pi ]$

ebenfalls eine bijektive Funktion. Mittels

$\arccos(x)+\arcsin(x)={\frac {\pi }{2}}$

lassen sich diese beiden Funktionen ineinander umrechnen.

Eigenschaften

	Arkussinus	Arkuskosinus
Funktionsgraph
Definitionsmenge	$[-1,1]$	$[-1,1]$
Bildmenge	$\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$	$[0,\pi ]$
Monotonie	streng monoton steigend	streng monoton fallend
Symmetrien	Ungerade Funktion (Punktsymmetrie zu $(0,0)$): $\arcsin(-x)=-\arcsin(x)$	Punktsymmetrie zu $\left(0,{\tfrac {\pi }{2}}\right)\colon$ $\arccos(x)=\pi -\arccos(-x)$
Asymptoten	keine	keine
Nullstellen	$0$	$1$
Sprungstellen	keine	keine
Polstellen	keine	keine
Extrema	Globales Maximum ${\tfrac {\pi }{2}}$ an der Stelle $1$, globales Minimum $-{\tfrac {\pi }{2}}$ an der Stelle $-1$	Globales Maximum $\pi$ an der Stelle $-1$, globales Minimum $0$ an der Stelle $1$
Wendepunkte	$(0,0)$	$\left(0,{\frac {\pi }{2}}\right)$

Formeln für negative Argumente

Aufgrund der Symmetrieeigenschaften gilt:

$\arcsin(-x)=-\arcsin(x)$

$\arccos(-x)=\pi -\arccos(x)$

Reihenentwicklungen

Die Taylorreihe des Arkussinus erhält man durch Entwickeln der Ableitung in eine binomische Reihe und anschließende Integration, sie ist gegeben durch:

${\begin{aligned}\arcsin(x)&=\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}=\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}\\&={x+{\frac {1}{2}}\cdot {\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {x^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {x^{7}}{7}}+\dotsb }\end{aligned}}$

Der Ausdruck $k!!$ bezeichnet dabei die Doppelfakultät.

Die Taylorreihe des Arkuskosinus ergibt sich aus der Beziehung $\arccos x={\tfrac {\pi }{2}}-\arcsin x$:

$\arccos(x)={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}$

Beide Reihen haben den Konvergenzradius 1.

Integraldarstellungen

Die Integraldarstellungen des Arkussinus bzw. Arkuskosinus sind gegeben durch:

$\arcsin(x)=\int \limits _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}$

$\arccos(x)=\int \limits _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}$

Verkettungen mit Sinus und Kosinus

Für die Arkusfunktionen gelten unter anderem folgende Formeln:

$\sin(\arccos(x))={\sqrt {1-x^{2}}}$, denn für $y=\arccos(x)$ gilt $y\in \left[0,{\pi }\right]$ und $\sin(y)={\sqrt {1-\cos ^{2}(y)}}$.

$\cos(\arcsin(x))={\sqrt {1-x^{2}}}$, denn für $y=\arcsin(x)$ gilt $y\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$ und $\cos(y)={\sqrt {1-\sin ^{2}(y)}}$.

$\sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}$, denn für $y=\arctan(x)$ gilt $y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[$ und $\sin(y)={\frac {\tan(y)}{\sqrt {1+\tan ^{2}(y)}}}$.

$\cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}$, denn für $y=\arctan(x)$ gilt $y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[$ und $\cos(y)={\frac {1}{\sqrt {1+\tan ^{2}(y)}}}$.

Beziehung zum Arkustangens

Von besonderer Bedeutung in älteren Programmiersprachen ohne implementierte Arkussinus- und Arkuskosinusfunktion sind folgende Beziehungen, die es ermöglichen, den Arkussinus und Arkuskosinus aus dem vielleicht implementierten Arkustangens zu berechnen. Aufgrund obiger Formeln gilt

$\arcsin(x)=\operatorname {sgn}(x)\cdot \arctan \left({\sqrt {\frac {x^{2}}{1-x^{2}}}}\right)$

$\arccos(x)={\frac {\pi }{2}}-\operatorname {sgn}(x)\cdot \arctan \left({\sqrt {\frac {x^{2}}{1-x^{2}}}}\right)$

für $|x|<1.$ Definiert man $\arctan \left({\tfrac {1}{0}}\right):=\lim _{t\to \infty }\arctan(t)={\tfrac {\pi }{2}},$ so werden diese beiden Gleichungen auch für $x=\pm 1$ richtig. Alternativ dazu kann man auch

$\arcsin(x)=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)$

$\arccos(x)={\frac {\pi }{2}}-2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)$

verwenden, was sich aus Obigem durch Anwenden der Funktionalgleichung des Arkustangens ergibt und für $|x|\leq 1$ gilt. Für $-1<x\leq 1$ lässt sich Letzteres auch zu

$\arccos(x)=2\arctan \left({\sqrt {\frac {1-x}{1+x}}}\right)$

vereinfachen.

Additionstheoreme

→ Hauptartikel: Additionstheoreme für Arkusfunktionen (Trigonometrie)

Die Additionstheoreme für Arkussinus und Arkuskosinus erhält man mit Hilfe der Additionstheoreme für Sinus und Kosinus:

$\arcsin x+\arcsin y=\left\{{\begin{matrix}\arcsin(\sin(\arcsin x+\arcsin y))=\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}xy\leq 0{\text{ oder }}x^{2}+y^{2}\leq 1\\\pi -\arcsin(\sin(\arcsin x+\arcsin y))=\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x>0{\text{ und }}y>0{\text{ und }}x^{2}+y^{2}>1\\-\pi -\arcsin(\sin(\arcsin x+\arcsin y))=-\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x<0{\text{ und }}y<0{\text{ und }}x^{2}+y^{2}>1\\\end{matrix}}\right.$$\arccos x+\arccos y=\left\{{\begin{matrix}\arccos(\cos(\arccos x+\arccos y))=\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn }}x+y\geq 0\\2\pi -\arccos(\cos(\arccos x+\arccos y))=2\pi -\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn }}x+y<0\\\end{matrix}}\right.$

Daraus folgt insbesondere für doppelte Funktionswerte

$2\arcsin x=\left\{{\begin{matrix}\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}2x^{2}\leq 1\\\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x>0{\text{ und }}2x^{2}>1\\-\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x<0{\text{ und }}2x^{2}>1\\\end{matrix}}\right.$

$2\arccos x=\left\{{\begin{matrix}\arccos \left(2x^{2}-1\right)&{\text{wenn }}x\geq 0\\2\pi -\arccos \left(2x^{2}-1\right)&{\text{wenn }}x<0\\\end{matrix}}\right.$

Ableitungen

Arkussinus

${\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1$

Arkuskosinus

${\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1$

Umrechnung

${\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)$

Integrale

Arkussinus

$\int \arcsin \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arcsin \left({\frac {x}{a}}\right)+{\sqrt {a^{2}-x^{2}}}+C$

Arkuskosinus

$\int \arccos \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arccos \left({\frac {x}{a}}\right)-{\sqrt {a^{2}-x^{2}}}+C$

Komplexe Argumente

${\begin{aligned}\arcsin(a+b\,\mathrm {i} )=\quad {\frac {\operatorname {sgn^{+}} {a}}{2}}\cdot \arccos &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}-(a^{2}+b^{2})\right)\\+\;\mathrm {i} \cdot {\frac {\operatorname {sgn^{+}} {b}}{2}}\cdot \operatorname {arcosh} &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}+(a^{2}+b^{2})\right)\end{aligned}}$   mit $a,b\in \mathbb {R}$

$\arccos(a+b\,\mathrm {i} )={\frac {\pi }{2}}-\arcsin(a+b\,\mathrm {i} )$

Zur Funktion $\operatorname {arcosh}$ siehe Areakosinus hyperbolicus, und für die Funktion $\operatorname {sgn^{+}} \colon \mathbb {R} \to \{-1,1\}$ gilt

$\operatorname {sgn^{+}} (x):=2\cdot \Theta (x)-1={\begin{cases}+1&{\text{für }}x\geq 0\\-1&{\text{für }}x<0\end{cases}}$

mit der Heaviside-Funktion $\Theta$.

Anmerkungen

Wichtige Funktionswerte

Siehe auch: Sinus und Kosinus: Wichtige Funktionswerte

Die folgende Tabelle listet die wichtigen Funktionswerte der beiden Arkusfunktionen auf.

$x$	$\arcsin(x)$		$\arccos(x)$
$0$	$0^{\circ }$	$0$	$90^{\circ }$	${\frac {\pi }{2}}$
${\frac {1}{2}}$	$30^{\circ }$	${\frac {\pi }{6}}$	$60^{\circ }$	${\frac {\pi }{3}}$
${\frac {1}{2}}{\sqrt {2}}$	$45^{\circ }$	${\frac {\pi }{4}}$	$45^{\circ }$	${\frac {\pi }{4}}$
${\frac {1}{2}}{\sqrt {3}}$	$60^{\circ }$	${\frac {\pi }{3}}$	$30^{\circ }$	${\frac {\pi }{6}}$
$1$	$90^{\circ }$	${\frac {\pi }{2}}$	$0^{\circ }$	$0$

Weitere wichtige Werte sind:

$x$	$\arcsin(x)$		$\arccos(x)$
${\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})$	$15^{\circ }$	${\tfrac {\pi }{12}}$	$75^{\circ }$	${\tfrac {5\pi }{12}}$
${\tfrac {1}{4}}\left({\sqrt {5}}-1\right)$	$18^{\circ }$	${\tfrac {\pi }{10}}$	$72^{\circ }$	${\tfrac {2\pi }{5}}$
${\tfrac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}$	$36^{\circ }$	${\tfrac {\pi }{5}}$	$54^{\circ }$	${\tfrac {3\pi }{10}}$
${\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)$	$54^{\circ }$	${\tfrac {3\pi }{10}}$	$36^{\circ }$	${\tfrac {\pi }{5}}$
${\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}$	$72^{\circ }$	${\tfrac {2\pi }{5}}$	$18^{\circ }$	${\tfrac {\pi }{10}}$
${\tfrac {1}{4}}({\sqrt {6}}+{\sqrt {2}})$	$75^{\circ }$	${\tfrac {5\pi }{12}}$	$15^{\circ }$	${\tfrac {\pi }{12}}$

Kettenbruchdarstellung des Arkussinus

H. S. Wall fand 1948 für den Arkussinus folgende Darstellung als Kettenbruch:

$\arcsin(x)={\frac {x{\sqrt {1-x^{2}}}}{1-{\cfrac {1\cdot 2x^{2}}{3-{\cfrac {1\cdot 2x^{2}}{5-{\cfrac {3\cdot 4x^{2}}{7-{\cfrac {3\cdot 4x^{2}}{9-{\cfrac {5\cdot 6x^{2}}{11-\ldots }}}}}}}}}}}}$

Komplexe Funktion

Man kann Arkussinus und Arkuskosinus auch durch den Hauptzweig des komplexen Logarithmus ausdrücken:

$\arcsin z=-\mathrm {i} \,\ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)$

$\arccos z=-\mathrm {i} \,\ln \left(z+\mathrm {i} {\sqrt {1-z^{2}}}\right)$

Diese beiden Formeln kann man wie folgt herleiten:

Für $\arcsin z$:

${\begin{aligned}\sin(x)={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}\\{\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}=z\\\mathrm {e} ^{\mathrm {i} x}-{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}=2z\mathrm {i} \\(\mathrm {e} ^{\mathrm {i} x})^{2}-1=2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}-1=0\\\mathrm {e} ^{\mathrm {i} x}=-{\frac {-2z\mathrm {i} }{2}}\pm {\sqrt {\left({\frac {-2z\mathrm {i} }{2}}\right)^{2}-(-1)}}\\\mathrm {e} ^{\mathrm {i} x}=z\mathrm {i} \pm {\sqrt {1-z^{2}}}\\\mathrm {i} x=\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\arcsin z=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\end{aligned}}$

Für $\arccos z$:

${\begin{aligned}\cos(x)={\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}\\{\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}=z\\\mathrm {e} ^{\mathrm {i} x}+{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}=2z\\(\mathrm {e} ^{\mathrm {i} x})^{2}+1=2z\mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {e} ^{\mathrm {i} x}+1=0\\\mathrm {e} ^{\mathrm {i} x}=-{\frac {-2z}{2}}\pm {\sqrt {\left({\frac {-2z}{2}}\right)^{2}-1)}}\\\mathrm {e} ^{\mathrm {i} x}=z\pm {\sqrt {z^{2}-1}}\\\mathrm {i} x=\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\arccos z=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\end{aligned}}$

Siehe auch

• Formelsammlung Trigonometrie
• Trigonometrische Funktionen

Literatur

• Ilja Bronstein, Konstantin Semendjajew: Taschenbuch der Mathematik. B.G. Teubner, Stuttgart 1991. ISBN 3-87144-492-8.

Einzelnachweise

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus hyperbolicus und Kosinus hyperbolicus | Tangens hyperbolicus und Kotangens hyperbolicus | Sekans hyperbolicus und Kosekans hyperbolicus 

Areafunktionen
Areasinus hyperbolicus und Areakosinus hyperbolicus | Areatangens hyperbolicus und Areakotangens hyperbolicus | Areasekans hyperbolicus und Areakosekans hyperbolicus