Fano-Ebene

Die Fano-Ebene (nach dem italienischen Mathematiker Gino Fano) ist eine Inzidenzstruktur, die sich sowohl als linearer Raum als auch als projektive Ebene, zweidimensionaler projektiver Raum oder als Blockplan auffassen lässt.
In der synthetischen Geometrie ist sie das Minimalmodell einer projektiven Ebene. Ihr affiner Ausschnitt, der durch Ausschneiden einer projektiven Geraden entsteht, ist das Minimalmodell einer affinen Ebene.
Die Automorphismengruppe der Fano-Ebene ist die Gruppe ihrer Projektivitäten, symbolisch als dargestellt, da sie formal eine Faktorgruppe der allgemeinen linearen Gruppe ist, tatsächlich ist sie zu dieser isomorph. ist eine einfache Gruppe und zählt in der Klassifikation der endlichen einfachen Gruppen zu den kleinsten nichtkommutativen einfachen Gruppen. Sie zählt dort zu den Gruppen vom Lie-Typ.
Daneben werden im Sprachgebrauch der synthetischen Geometrie diejenigen projektiven oder (seltener) affinen Ebenen als Fano-Ebenen bezeichnet, in denen das Fano-Axiom gilt. Die Fano-Ebene, wie sie dieser Artikel beschreibt, ist in diesem axiomatischen Sinn keine Fano-Ebene, denn sie erfüllt das projektive Fano-Axiom nicht.
Definitionen[Bearbeiten | Quelltext bearbeiten]

Visualisierung, Definition als Hypergraph[Bearbeiten | Quelltext bearbeiten]
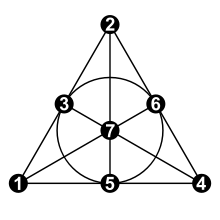
Die Fano-Ebene lässt sich durch die Zeichnung eines gleichseitigen Dreiecks mit Höhen und Inkreis visualisieren (erste Abbildung oben) und definieren. Die 7 Elemente von , die Punkte, sind die drei Eckpunkte, die drei Höhenfußpunkte und der Mittelpunkt des Inkreises. Die 7 Elemente von , die Geraden, sind dann die Dreieckseiten, die Höhen und der Inkreis. Aus dem Satz von Sylvester-Gallai folgt, dass es keine Darstellung gibt, bei der alle Geraden tatsächlich Geraden der euklidischen Ebene sind. Dieses Bild kann – im Sinne der Graphentheorie – als ein Hypergraph mit Knoten (den Punkten) und Kanten (den Strecken und dem Inkreis) und damit als Modell der Fano-Ebene angesehen werden.
Konkrete, aufzählende Definition als Inzidenzstruktur[Bearbeiten | Quelltext bearbeiten]
Die folgende (symmetrische) Inzidenzstruktur wird als Fano-Ebene bezeichnet:
- Punktmenge: oder
- Geradenmenge: oder
- Inzidenzrelation : Für gilt und
In dieser konkreten Definition durch Aufzählung können die 7 „binären“ Punktsymbole (vergleiche die Abbildung rechts: usw.) einfach als eigenwillige Symbole für 7 verschiedene Punkte genommen werden. Tatsächlich stehen sie abkürzend für Koordinatentripel, wie weiter unten erläutert wird. Die zweite, kompaktere Darstellung der Punkte- und Geradenmenge entsteht jeweils durch die Interpretation dieser Punktsymbole als Zahlen im Dualsystem und deren Umrechnung ins Dezimalsystem.
Definition als projektiver Raum[Bearbeiten | Quelltext bearbeiten]
Gleichwertig lässt sich die Fano-Ebene mit der Sprache der linearen Algebra definieren als der zweidimensionale projektive Raum über dem endlichen Körper mit zwei Elementen. Dieser Körper wiederum kann durch den Restklassenkörper modelliert werden.
Äquivalenz der Definitionen[Bearbeiten | Quelltext bearbeiten]
Die Fano-Ebene ist im Sinne der synthetischen Geometrie eine endliche projektive Ebene der Ordnung 2 mit 7 Geraden und 7 Punkten, ihre symbolische Abkürzung lautet . Bei der axiomatischen Beschreibung projektiver Ebenen ergibt sich dies, indem man direkt anhand der konkret definierten Inzidenzstruktur die Gültigkeit der Axiome überprüft.
Bei der Definition als zweidimensionaler projektiver Raum über dem Körper betrachtet man den Vektorraum , dessen eindimensionalen Unterräume sind dann die Punkte der projektiven Ebene, seine zweidimensionalen Unterräume die Geraden und die Inzidenzrelation ist die mengentheoretische Teilmengenrelation „“. Somit erhält man (formal)
- als Punktmenge: und
- als Geradenmenge: .
Dabei stehen die Symbole für die von dem Vektor bzw. den Vektoren erzeugten linearen Unterräume des . Die Bedingung in der Definition der Geradenmenge ist für diesen Vektorraum gleichwertig zur linearen Unabhängigkeit der zwei Vektoren, solange der Nullvektor ausgeschlossen wird.
Punktkoordinaten[Bearbeiten | Quelltext bearbeiten]
Nun kann man im visualisierten Modell (gleichseitiges Dreieck mit Höhen und Inkreis) ein vollständiges Viereck, also eine geordnete, vierelementige Punktmenge , bei der keine drei Punkte auf einer Geraden liegen, als projektive Punktbasis auswählen und diesen Punkten in der gegebenen Reihenfolge die (Erzeugnisse der) Standardbasis des nebst Einheitspunkt zuweisen: usw. – formal genauer: , denn der projektive Punkt entspricht einem eindimensionalen Unterraum, also dem Erzeugnis von . Nun wird die Schreibweise noch etwas informeller gemacht und weiter verkürzt: Wir vereinbaren als Abkürzung für die oben beschriebene Zuordnung.
In der zweiten Abbildung oben wurde dies durchgeführt. Dabei wurden die Ecken in der Reihenfolge „rechts 100, oben 010, links 001“ zu den ersten drei Basispunkten und der Höhenschnittpunkt zum Einheitspunkt , die Koordinaten der übrigen Punkte ergeben sich so: Der dritte Punkt auf einer Geraden muss sich durch binäre Addition ohne Überträge (auch Exclusiv-Oder-Verknüpfung XOR genannt) der anderen beiden Punkte auf der Geraden ergeben. Zum Beispiel: , in Worten: Der Mittelpunkt der unteren Seite des gleichseitigen Dreiecks (101) liegt auf der unteren Seite (erste „Summe“), der Höhe zu dieser Seite (zweite „Summe“) und auf dem Inkreis (dritte „Summe“). Dass diese Gleichungen für die „Summen“ aufgehen, bedeutet nun gerade, dass der Vektor im jeweiligen Erzeugnis der summierten, verschiedenen Koordinatenvektoren liegt. Da die drei Seitenmitten, also gerade die Punkte, die nicht zum vollständigen Viereck gehören, mit dieser Regel konsistent koordinatisiert werden können, ist die „Visualisierung als gleichseitiges Dreieck“, formal genauer: der entsprechende Hypergraph zu isomorph. Die Definition durch Aufzählung gibt nun aber einfach die Punktmenge und Geradenmenge des Hypergraphen wieder und ist daher zu den beiden anderen Modellen isomorph.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
- Die Fano-Ebene ist ein zweidimensionaler projektiver Raum über einem endlichen Körper im Sinne der linearen Algebra.
- Damit ist sie auch ein linearer Raum.
- Sie ist eine pappussche zweidimensionale projektive Geometrie und also eine projektive Ebene im Sinne der synthetischen Geometrie.
- Jede projektive Ebene der Ordnung 2 ist zur Fano-Ebene isomorph und es existiert keine projektive Ebene kleinerer Ordnung.[1]
- Sie ist ein symmetrischer (7,3,1)-Blockplan, damit ist sie der kleinste Hadamard-Blockplan.
Entartungen[Bearbeiten | Quelltext bearbeiten]
Durch ihre Kleinheit weist die Fano-Ebene einige Besonderheiten auf:
- Sie erfüllt den Satz von Pappos sozusagen „leer“: Da es keine nichtentarteten Sechsecke der Art, wie sie die Pappos-Konfiguration erfordert, gibt, fallen (mindestens) zwei der sechs Ecken zusammen. Dann fallen aber auch mindestens zwei „Schnittpunkte von Gegenseiten“ zusammen und die Aussage des Satzes, dass diese drei Schnittpunkte auf einer Geraden liegen, wird trivial.
- Da eine nicht entartete Desargues-Konfiguration zehn verschiedene Punkte erfordert, wird auch der Satz von Desargues letztendlich trivial erfüllt.
- Sie ist die einzige projektive Ebene über einem Schiefkörper, in der jede projektive Perspektivität mit einem Zentrum außerhalb einer Achse zwingend die Identität ist. Durch die Vorgaben sind die „freien“ Punktmengen auf den Geraden durch das Zentrum einpunktig (mindestens ein Punkt jeder dieser Geraden liegt auf , ein weiterer ist das Zentrum). Also wird auch die Transitivitätsforderung an Ebenen der Lenz-Barlotti-Klasse VII.2 leer erfüllt. Dieser Klasse VII.2 gehört die Fano-Ebene also wie jede andere desarguessche Ebene an.
- Das Doppelverhältnis ist entartet, da es auf keiner Geraden vier verschiedene Punkte gibt.
- Die Fano-Ebene ist die einzige projektive Ebene, in der der Einheitspunkt zur Definition einer projektiven Punktbasis eigentlich überflüssig ist: Im Vektorraummodell enthält jeder eindimensionale Raum neben dem Nullvektor nur einen weiteren Punkt, das heißt, die indirekte Zuordnung „Basisvektor → eindimensionaler Unterraum ↔ projektiver Punkt“ ist hier auch zum Basisvektor hin umkehrbar, ohne dass ein Einheitspunkt zu Hilfe genommen werden muss; dies gilt ganz genau so für die projektiven Räume beliebiger Dimension , wenn, aber auch nur dann, wenn der Körper genau zwei Elemente hat. Bei der Wahl der Punktbasis in der Ebene zeigt sich diese Besonderheit so: Hat man für die Punktbasis drei nicht kollineare Punkte gewählt – für diese Wahl gibt es bei Berücksichtigung der Reihenfolge immerhin Möglichkeiten – dann gibt es stets genau noch einen Punkt in der Ebene, der nicht zu zwei der gewählten Punkte kollinear ist!
- In der Automorphismengruppe von drückt sich die zuletzt genannte Besonderheit dadurch aus, dass aus der für beliebige Körper gültigen Isomorphieaussage die Aussage folgt, denn die multiplikative Gruppe ist für den zweielementigen Körper die Einsgruppe.
Dualisierung[Bearbeiten | Quelltext bearbeiten]

Eine abstrakte Dualisierung der Fano-Ebene erhält man, indem man in einer der Definitionen Punktmenge und Geradenmenge vertauscht und die Inzidenzrelation umkehrt, also die Inzidenzstruktur [2] betrachtet. Die so aus abgeleitete Inzidenzstruktur ist stets wieder eine Inzidenzstruktur und für eine projektive Ebene (im Sinne der synthetischen Geometrie) auch wieder eine projektive Ebene derselben Ordnung. Für desarguessche projektive Ebenen und also auch für die Fano-Ebene ist die duale Struktur zur Ausgangsstruktur isomorph. Dies zeigt man mit Hilfe eines konkreten Isomorphismus (einer Korrelation), der vom gewählten Koordinatensystem abhängt. Eine solche Korrelation (hier genauer: eine projektive, hyperbolische Polarität) wird im nachfolgenden Abschnitt beschrieben:
Geradenkoordinaten und Dualität[Bearbeiten | Quelltext bearbeiten]
Im Vektorraummodell lässt sich jede Gerade, also jeder zweidimensionale Unterraum des durch eine homogene Geradengleichung beschreiben. Der Koordinatenvektor der Geraden (Geradenkoordinaten) ist also . Einem Punkt mit den projektiven Punktkoordinaten wird die Gerade mit den homogenen Geradenkoordinaten zugeordnet und umgekehrt. Die Abbildung rechts zeigt die Zuordnungen für die in diesem Artikel getroffene Wahl der Punktbasis: Die Punkte unten im Bild werden durch diese Korrelation den Geraden, die direkt über ihnen stehen, zugeordnet, die Geraden dem direkt unter ihnen stehenden Punkt. Zum Beispiel wird der 3. Basispunkt 001, der rechte untere Eckpunkt des Dreiecks, der Geraden mit der Gleichung (der linken Dreieckseite) zugeordnet , die Höhe durch die obere Spitze mit der Gleichung ihrem Höhenfußpunkt 101.
Im Bild rechts stellen die Strecken in der Mitte zwischen den rot hervorgehobenen Geraden und Punkten die Inzidenzrelation dar, die durch die Dualisierung umgekehrt wird: , bzw. mengentheoretisch , im Vektorraummodell , wobei das Kleinerzeichen für „ist linearer Teilraum von“ steht.
Kollineationsgruppe[Bearbeiten | Quelltext bearbeiten]
Die Automorphismengruppe der Fano-Ebene ist die Gruppe ihrer Kollineationen; sie stimmt mit der Gruppe ihrer Projektivitäten überein, da der zweielementige Primkörper keine nichtidentischen Körperautomorphismen zulässt. Sie operiert scharf transitiv auf den geordneten nichtkollinearen Punktetripeln und hat daher die Ordnung , die gleiche Ordnung ergibt sich aus der Formel für die Ordnung der allgemeinen linearen Gruppe. Sie ist nichtabelsch und einfach (d. h. sie hat nur die trivialen Normalteiler).
Bei den folgenden, gruppentheoretischen Betrachtungen wird als Gruppe von Permutationen ihrer Punkte, also als Untergruppe der symmetrischen Gruppe dargestellt. Dabei wird vereinbart, dass Permutationen von links auf Zahlen operieren, das heißt, es gilt und z. B. . In der Sprache der Geometrie sind zwei Projektivitäten genau dann zueinander konjugiert, wenn bezüglich einer geeigneten Punktbasis die gleiche Darstellung wie bezüglich unserer Ausgangsbasis (als lineare Abbildung) hat. In der Permutationsdarstellung heißt das, die Ebene kann nach dem oben beschriebenen „binären“ System so umnummeriert werden, dass die Permutationsdarstellung von annimmt. Zwei Permutationen sind in der genau dann konjugiert, wenn sie gleichartige Darstellungen als Produkte von disjunkten Zyklen haben, diese Bedingung ist also auch in notwendig, sie erweist sich dort auch – außer für die Elemente der Ordnung 7, die in zwei Konjugationsklassen zerfallen – als hinreichend.
2-Gruppen und Perspektivitäten[Bearbeiten | Quelltext bearbeiten]

- Zu jeder der 7 Geraden existiert eine Gruppe von ebenen Perspektivitäten mit als Achse. Hat eine -Perspektivität einen weiteren Fixpunkt außerhalb der Achse, dann ist sie die Identität, da jede Gerade nur drei Punkte hat. Daher haben alle nichtidentischen Perspektivitäten ihr Zentrum auf der Achse und vertauschen die beiden Punkte, die außer jeweils auf den beiden von der Achse verschiedenen Geraden durch liegen:
- Die Gruppe der Perspektivitäten mit Achse und Zentrum ist , eine zyklische Gruppe mit zwei Elementen vom Isomorphietyp .
- Alle Perspektivitätengruppen mit fester Achse (7 Geraden) und festem Zentrum (je 3 Punkte) sind isomorph zu der im Beispiel genannten und also zu . Diese Gruppen sind in zueinander konjugiert, die Menge dieser zweielementigen Gruppen ist zu sich selbst dual. Die 21 nichttrivialen Elemente dieser Gruppen erzeugen die , denn sie bilden gerade die Menge aller nichtidentischen Perspektivitäten. Daher ist diese Automorphismengruppe eine Untergruppe der alternierenden Gruppe und zählt zu den Coxeter-Gruppen, da sie von Elementen der Ordnung 2 („Spiegelungen“) erzeugt wird.
- Jede Projektivität in der Ordnung 2 hat eine Permutationsdarstellung als Element der , wobei die vier verschiedenen Zahlen für die Punkte eines vollständigen Vierecks stehen. Daher ist jede solche Projektivität der Ordnung 2 die nichttriviale Perspektivität mit Achse und Zentrum und alle diese Perspektivitäten sind zueinander konjugiert.
- Die Gruppe der Perspektivitäten mit Achse ist also diese vierelementige Gruppe ist isomorph zur kleinschen Vierergruppe , einer elementar abelschen 2-Gruppe.
- Alle 7 Perspektivitätenuntergruppen mit fester Achse sind konjugiert zu und also isomorph zu . Eine solche Gruppe stellt zugleich in der längs geschlitzten Ebene, dem Minimalmodell einer affinen Ebene, die Dilatationsgruppe und in diesem Fall zugleich die Translationsgruppe dar. Dies zeigt auch ohne Nachrechnen mit den Permutationen, dass gelten muss.
- Die genannten Perspektivitätenuntergruppen mit fester Achse sind dual, aber nicht konjugiert zu 7 verschiedenen Perspektivitätenuntergruppen mit festem Zentrum . Jede solche Gruppe ist also ebenfalls zur isomorph, jede Gerade durch ist eine Fixgerade der Gruppe. Ein Beispiel ist , also .
- Das Erzeugnis ist für eine 2-Sylow-Untergruppe von mit 8 Elementen. Alle 21 2-Sylow-Untergruppen von sind zueinander konjugiert, isomorph zu der Diedergruppe . Ein Beispiel ist die Untergruppe , einer ihrer hier genannten Erzeuger ist rechts graphisch dargestellt.
- Alle 42 Elemente der Ordnung 4 in sind konjugiert zu , dem in der Abbildung rechts dargestellten Erzeuger von . Sie sind also keine Perspektivitäten, bestehen alle aus einem 4-Zyklus , der vier Punkte in allgemeiner Lage zyklisch vertauscht und einer Transposition von 2 der drei übrigen Punkte, die auf einer Geraden liegen. Die Transposition ist dadurch bestimmt, dass sie das Zentrum der Perspektivität fix lässt. In unserem Beispiel ist 1 das Zentrum von und also auch der Fixpunkt von .
3-Gruppen und die Affinitätengruppe[Bearbeiten | Quelltext bearbeiten]
- Sind die Punkte auf einer Geraden, so erzeugen zwei der Perspektivitätsgruppen zusammen eine Untergruppe von mit 24 Elementen. Zum Beispiel ist als Erzeugnis von Perspektivitäten das Produkt dieser drei Erzeugenden ist das Element , ein Element der Ordnung 3. Dieses Element ist bereits in zu seinem inversen konjugiert, daher enthält eine zur Diedergruppe isomorphe Untergruppe. Als Untergruppe mit 24 Elementen enthält drei der 2-Sylowgruppen der Kollineationsgruppe mit 8 Elementen: für
- Die Gruppe ist isomorph zur symmetrischen Gruppe , denn sie bildet die Gerade als Fixgerade auf sich ab und operiert daher treu auf der längs geschlitzten Ebene als Gruppe von Affinitäten. Die volle Affinitätengruppe der affinen Ebene mit 4 Punkten ist aber gerade die .
- Alle 56 Elemente der Ordnung 3 sind zueinander konjugiert und zu , sie haben also immer die Form eines Produktes aus zwei disjunkten 3-Zyklen, wobei der eine Zyklus kollineare Punkte enthält, der andere 3 der vier nicht kollinearen Punkte außerhalb der durch den ersten Zyklus bestimmten Geraden.
- Jede der 28 3-Sylowgruppen der Gruppenordnung 3 wird von einem der genannten Elemente der Ordnung 3 erzeugt.
7-Gruppen und kleine Erzeugendensysteme[Bearbeiten | Quelltext bearbeiten]

- In existieren genau 48 Projektivitäten der Ordnung 7, die jeweils als ein 7-Zyklus darstellbar sind.
- Jedes dieser Gruppenelemente erzeugt eine 7-Sylowgruppe von vom Isomorphietyp , die insgesamt 6 7-Zykeln enthält. Zwei verschiedene dieser 7-Sylowgruppen schneiden sich in der trivialen Gruppe, daher existieren genau 8 Untergruppen dieses Typs.
- Die Menge der 7-Zykeln zerfällt in in zwei Konjugationsklassen mit je 24 Elementen.
- Jeder 7-Zyklus ist durch beliebige vier Punkte , die er in dieser Reihenfolge aufeinander abbildet vollständig bestimmt, wobei nicht kollinear sind und stets
- entweder auf der Verbindungsgerade (erste Konjugationsklasse)
- oder auf der Verbindungsgerade (zweite Konjugationsklasse) liegt.
- Ist ein Element der Ordnung 7 (7-Zyklus), dann ist genau dann konjugiert zu , wenn ein Quadratischer Rest modulo 7 ist, das heißt, liegen in der gleichen Konjugationsklasse wie und in der anderen.
- Die von einem 7-Zyklus erzeugte zyklische Kollineationsgruppe ist ein Singer-Zyklus, daher existiert für jeden 7-Zyklus eine Bijektion („Umnummerierung“) der Punktmenge, nach der die umnummerierte Fano-Ebene von der Differenzenmenge abstammt.[3]
- Sind zwei Projektivitäten der Ordnung 7, dann gilt nach den Sylowsätzen und da einfach ist: oder . Das heißt, die Automorphismengruppe wird von zwei geeignet gewählten 7-Zykeln erzeugt, zum Beispiel: mit
- Jeder 7-Zyklus ist als Komposition von genau drei verschiedenen, nichtidentischen Perspektivitäten darstellbar. Für die beiden Zyklen aus der vorigen Aussage ist bzw. mit den Perspektivitäten .
- Daraus folgt: als Erzeugnis von drei Perspektivitäten und [4] als Erzeugnis einer Perspektivität und einer Projektivität der Ordnung 4.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Die Multiplikation der Oktonionen kann man in der Fano-Ebene darstellen.
Literatur[Bearbeiten | Quelltext bearbeiten]
Allgemein[Bearbeiten | Quelltext bearbeiten]
- Peter Dembowski: Finite geometries. Reprint of the 1968 Auflage. Springer, Berlin/Heidelberg/Singapore/Tokyo/New York/Barcelona/Budapest/Hong Kong/London/Milan/Paris/Santa Clara 1997, ISBN 3-540-61786-8.
- Jacobus Hendricus van Lint, Richard M. Wilson: A Course in Combinatorics. Nachdruck der 2. Auflage. Cambridge Univ. Press, Cambridge u. a. 2004, ISBN 0-521-00601-5, S. 225, 237–239 (Auszug in der Google-Buchsuche).
- T. Pisanski, M. Randić: Bridges between Geometry and Graph Theory. In: C. A. Gorini (Hrsg.): Geometry at Work. A Collection of Papers Showing Applications of Geometry. Math. Assoc. Amer., Washington, DC 2000, S. 174–194.
Anwendungen der Fano-Ebene auf mathematische Rätsel[Bearbeiten | Quelltext bearbeiten]
- David Wells: The Penguin Dictionary of Curious and Interesting Geometry. 1. Auflage. Penguin, London 1986, ISBN 0-14-008029-5 (englisch, Recreational mathematics, elementary number theory).
Zu den gruppentheoretischen Aussagen[Bearbeiten | Quelltext bearbeiten]
- Thomas W. Hungerford: Algebra. korrigierte 5. Auflage. Springer, Berlin/Heidelberg/New York 2003, ISBN 0-387-90518-9, Kapitel I Groups, 5–7.
- Bartel Leendert van der Waerden: Algebra. Unter Benutzung von Vorlesungen von E. Artin und E. Noether. 9. Auflage. Band 1. Springer, Berlin/Heidelberg/New York 1993, ISBN 3-540-56799-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Fano Plane. In: MathWorld (englisch).
- Endliche Ebene und Fano-Ebene bei PlanetMath (englisch)
- Die Gruppe der Walsh-Permutationen (siehe v:en:3-bit Walsh permutation) auf einer 8-elementigen Menge ist isomorph zur Automorphismengruppe der Fano-Ebene.
Einzelnachweise und Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Dembowski (1968), Kapitel 1
- ↑ Die Inzidenzrelation ist nach Definition wie in jeder projektiven Ebene symmetrisch, daher ist und
- ↑ Man wähle zu dem 7-Zyklus c diejenige der Potenzen , die in der ersten Konjugationsklasse liegt, dann gibt es eine solche Bijektion , durch die wird.
- ↑ Beachte, dass alle Perspektivitäten involutorisch sind und daher ist.













































































































































