Urnenmodell

Ein Urnenmodell ist ein Gedankenexperiment, das in der Wahrscheinlichkeitstheorie, Statistik und Kombinatorik verwendet wird, um verschiedene Zufallsexperimente auf einheitliche und anschauliche Weise zu modellieren. Dazu wird ein fiktives Gefäß, Urne genannt, mit einer bestimmten Anzahl an Kugeln gefüllt, die anschließend zufällig gezogen werden. Damit ist gemeint, dass bei jedem Zug alle in der Urne befindlichen Kugeln die gleiche Wahrscheinlichkeit haben, ausgewählt zu werden. Dadurch kann die Bestimmung interessierender Wahrscheinlichkeiten auf die Lösung kombinatorischer Abzählprobleme zurückgeführt werden.
Im einfachsten Urnenmodell unterscheidet man Ziehungen mit Zurücklegen, bei denen jede Kugel nach ihrer Registrierung wieder in die Urne zurückgelegt wird, von Ziehungen ohne Zurücklegen, bei denen eine einmal gezogene Kugel nicht wieder zurückgelegt wird. Bei der Registrierung der gezogenen Kugeln unterscheidet man, ob die Reihenfolge der gezogenen Kugeln entweder beachtet oder nicht beachtet, d. h. außer Acht gelassen wird.
Viele wichtige Wahrscheinlichkeitsverteilungen, wie beispielsweise die diskrete Gleichverteilung, die Binomialverteilung, die Bernoulli-Verteilung, die hypergeometrische Verteilung, die negative Binomialverteilung, die geometrische Verteilung, die negative hypergeometrische Verteilung, die Multinomialverteilung oder die multivariate hypergeometrische Verteilung, können mit Hilfe von Urnenmodellen hergeleitet und veranschaulicht werden.
Geschichte[Bearbeiten | Quelltext bearbeiten]

Auch wenn sich das Konzept des Urnenmodells bis in das Alte Testament und das antike Griechenland zurückverfolgen lässt, geht seine erste explizite Erwähnung in einem mathematischen Kontext auf den Schweizer Mathematiker Jakob I Bernoulli zurück.[1] Zu Beginn des dritten Teils seines berühmten Werks Ars Conjectandi aus dem Jahr 1713 beschreibt Bernoulli folgendes Problem:
„Jemand setzt, nachdem er zwei Steine, einen schwarzen und einen weissen, in eine Urne gelegt hat, für drei Spieler A, B, C einen Preis aus unter der Bedingung, dass ihn derjenige erhalten soll, welcher zuerst den weissen Stein zieht; wenn aber keiner der drei Spieler den weissen Stein zieht, so erhält auch keiner den Preis. Zuerst zieht A und legt den gezogenen Stein wieder in die Urne, dann thut B als Zweiter das Gleiche, und schliesslich folgt C als Dritter. Welche Hoffnungen haben die drei Spieler?“
Hierbei ist mit „Hoffnung“ die Gewinnerwartung eines Spielers gemeint. Bernoulli verwendete in seinem in lateinischer Sprache geschriebenen Werk die Begriffe urna für eine Wahlurne und calculi für Zählsteine. Solche mit Loskugeln gefüllte Wahlurnen kamen unter anderem in der Republik Venedig bei der Wahl des Dogen zum Einsatz. Die grundlegende Idee hinter einem solchen Urnenmodell war für Bernoulli das Konzept der gleichen Wahrscheinlichkeit, mit der ein beliebiger Stein aus der Urne gezogen wird. Darauf basierend lassen sich nun die Gewinnerwartungen der drei Spieler ermitteln: Spieler A gewinnt in 50 % der Fälle, Spieler B in 25 % der Fälle, Spieler C in 12,5 % der Fälle und keiner der drei Spieler ebenfalls in 12,5 % der Fälle.
Ähnliche Urnenprobleme wurden im 18. Jahrhundert auch von Daniel Bernoulli und Pierre Rémond de Montmort betrachtet.[3] Abraham de Moivre und Thomas Bayes setzten sich in dieser Zeit im Kontext der Inferenzstatistik speziell mit der Frage auseinander, ob sich aus der Beobachtung der gezogenen Kugeln auf die Anteile der Kugeln in der Urne schließen lässt. Knapp einhundert Jahre nach Bernoulli griff Pierre-Simon Laplace die Idee in seiner Théorie Analytique des Probabilités wieder auf und stellte dabei die Wahrscheinlichkeitstheorie auf eine solide mathematische Grundlage.[1]
Heute sind Urnenmodelle ein zentraler Bestandteil der Grundausbildung in der Stochastik, insbesondere der Wahrscheinlichkeitstheorie, Statistik und Kombinatorik.
Beschreibung des Urnenmodells[Bearbeiten | Quelltext bearbeiten]

In einer Urne befinden sich mehrere Kugeln, die verschiedene Ausprägungen von Eigenschaften aufweisen können, z. B. unterschiedlich gefärbt oder unterschiedlich beschriftet sind, ansonsten aber gleich sind. Aus dieser Urne wird nun eine Kugel herausgenommen und registriert. Hierbei wird angenommen, dass bei einer solchen Ziehung eine Kugel zufällig ausgewählt wird, d. h., es soll nicht vorhersehbar sein, welche der Kugeln gezogen wird. Weiter wird angenommen, dass jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird, da die Kugeln gut durchmischt in der Urne liegen. Dieser Vorgang des Ziehens kann nun mehrmals wiederholt werden. Es lassen sich im einfachsten Urnenmodell 4 Fälle unterscheiden:
- Ziehen mit Zurücklegen unter Beachtung der Reihenfolge (Variation mit Wiederholung)
- Ziehen ohne Zurücklegen unter Beachtung der Reihenfolge (Variation ohne Wiederholung)
- Ziehen mit Zurücklegen ohne Beachtung der Reihenfolge (Kombination mit Wiederholung)
- Ziehen ohne Zurücklegen ohne Beachtung der Reihenfolge (Kombination ohne Wiederholung)
Bemerkung:
- Ziehen mit Zurücklegen: Jede Kugel wird nach ihrer Registrierung wieder in die Urne zurückgelegt; die Zahl der Kugeln in der Urne verändert sich damit bei mehreren Ziehungen nicht. Daher sind die Ziehungen unabhängig voneinander.
- Ziehen ohne Zurücklegen: Eine einmal gezogene Kugel wird nicht wieder zurückgelegt; die Zahl der Kugeln in der Urne verringert sich damit nach jeder Ziehung um eins. Daher sind die Ziehungen nicht voneinander unabhängig.
- Ziehen unter Beachtung der Reihenfolge: Die Kugel wird nach der Ziehung nicht nur einfach registriert, sondern es wird auch registriert, bei der wievielten Ziehung die Kugel gezogen wurde. Eine Anordnung der gezogenen Kugeln ist dadurch möglich.
- Ziehen ohne Beachtung der Reihenfolge: Die Kugeln werden nach der Ziehung registriert. Es wird nicht registriert, welche Kugel bei welcher Ziehung gezogen wurde. Eine Anordnung der gezogenen Kugeln ist nicht möglich. Es wird nur die Auswahl der gezogenen Kugeln registriert.
Im Folgenden wird der besonders anschauliche Fall einer Urne, die mit verschiedenfarbigen Kugeln gefüllt ist, betrachtet.
Ergebnismengen[Bearbeiten | Quelltext bearbeiten]
Einmaliges Ziehen[Bearbeiten | Quelltext bearbeiten]

In der Wahrscheinlichkeitstheorie werden Ergebnisse, etwa dass eine bestimmte Kugel gezogen wird, durch Mengen dargestellt. Im Urnenmodell geht man zunächst von unterschiedlichen Kugeln aus. Falls einige Kugeln in der Urne die gleiche Ausprägung der Eigenschaften haben, z. B. die gleiche Farbe haben, erweist es sich als vorteilhaft, die Kugeln durch eine Nummerierung voneinander zu unterscheiden. Befinden sich in der Urne insgesamt Kugeln, dann definiert man als Ergebnismenge für das Ziehen einer Kugel
- ,
wobei die Elemente der Ergebnismenge die einzelnen Kugeln identifizieren. Befinden sich beispielsweise drei rote, eine grüne und zwei blaue Kugeln in der Urne, so lässt sich die Ergebnismenge durch
beschreiben. Die Anzahl der Elemente der Ergebnismenge wird durch die Mächtigkeit der Ergebnismenge beschrieben. Die Mächtigkeit der Ergebnismenge ist identisch mit der Anzahl der Möglichkeiten, Kugeln aus einer Urne mit Kugeln zu ziehen.
Jedem Ergebnis , , wird nun eine Wahrscheinlichkeit zugeordnet. Nachdem jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird, handelt es sich hierbei um ein Laplace-Experiment, bei dem für die Wahrscheinlichkeit jedes Elements der Ergebnismenge
gilt. In obigem Beispiel mit sechs Kugeln erhält man also für jede Kugel die gleiche Wahrscheinlichkeit
- .
Ziehen mit Zurücklegen unter Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]

Beim Ziehen mehrerer Kugeln unter Beachtung der Reihenfolge werden die Ergebnisse durch Tupel dargestellt, wobei die Länge des Tupels der Anzahl der Ziehungen entspricht. Werden von den Kugeln in der Urne Kugeln mit Zurücklegen gezogen, dann hat die Ergebnismenge die Form
- .
Die Ergebnismenge ist damit das -fache kartesische Produkt der Ergebnismenge einer einfachen Ziehung. Man spricht hier auch von einer Variation mit Wiederholung. Nachdem es für jedes der Tupelelemente Möglichkeiten gibt, erhält man für die Anzahl der Elemente der Ergebnismenge
- .
Werden aus der Beispielurne mit sechs Kugeln drei Kugeln mit Zurücklegen unter Beachtung der Reihenfolge gezogen, dann hat jede zulässige Kugelkombination die Wahrscheinlichkeit
- .
Diese Wahrscheinlichkeit ist gerade das dreifache Produkt der Wahrscheinlichkeiten beim einmaligen Ziehen.
Ziehen ohne Zurücklegen unter Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]
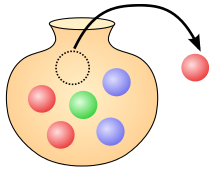
Auch beim Ziehen ohne Zurücklegen unter Beachtung der Reihenfolge werden die Ergebnisse durch Tupel dargestellt, wobei die Länge des Tupels der Anzahl der Ziehungen entspricht. Werden von den Kugeln in der Urne Kugeln ohne Zurücklegen gezogen, dann hat die Ergebnismenge die Form
- .
Die Ergebnismenge besteht damit aus allen -Tupeln, bei denen kein Element des Tupels mehr als einmal vorkommt. Man spricht hier auch von einer Variation ohne Wiederholung. Nachdem es für das erste Tupelelement Möglichkeiten gibt, für das zweite Möglichkeiten und so weiter, erhält man für die Anzahl der Elemente der Ergebnismenge
- .
Der Ausdruck wird fallende Faktorielle ab mit Faktoren genannt. Werden aus der Beispielurne mit sechs Kugeln drei Kugeln ohne Zurücklegen unter Beachtung der Reihenfolge gezogen, dann hat jede zulässige Kugelkombination die Wahrscheinlichkeit
- .
Diese Wahrscheinlichkeit ist gerade das Produkt der Wahrscheinlichkeiten beim jeweils einmaligen Ziehen aus einer Urne mit sechs, fünf und vier Kugeln.
Ziehen mit Zurücklegen ohne Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]
Eine adäquate mathematische Beschreibung dieses Falls ist durch eine Multimenge gegeben, die zum einen als Menge – im Gegensatz zu einem Tupel – Elemente in nicht angeordneter Weise zu beschreiben erlaubt, was für das Außer-Acht-Lassen der Reihenfolge der gezogenen Kugeln benötigt wird, und zum anderen ein mehrfaches Auftreten eines Elements innerhalb einer Menge erlaubt (Vielfachheit bzw. Multiplizität eines Elements), was für die Möglichkeit eines mehrfachen Ziehens einer Kugel notwendig ist, da eine gezogene Kugel wieder in die Urne zurückgelegt wird und erneut gezogen werden kann. Als Schreibweise für eine Multimenge wird hier gewählt und die Vielfachheit eines Elements steht in runden Klammern als hochgestellte Zahl am Element. Da eine Kugel maximal mal gezogen werden kann, ergibt sich die (Multi-)Menge zu
- .
Beim Ziehen mit Zurücklegen ohne Beachtung der Reihenfolge werden die Ergebnisse durch Teil(multi)mengen dargestellt:
- .
Für die Vielfachheit einer Kugel gilt , für , da die Anzahl möglicher Ziehungen einer Kugel zwischen und liegt. Befinden sich in einer Urne Kugeln und werden Kugeln mit Zurücklegen ohne Beachtung der Reihenfolge gezogen, ergibt sich als Ergebnismenge
- .
Man spricht hier auch von einer Kombination mit Wiederholung. Die Anzahl der Möglichkeiten, Ziehungen unter Kugeln mit Zurücklegen ohne Beachtung der Reihenfolge durchzuführen, ergibt sich aus der Anzahl der Möglichkeiten, die Gleichung zu erfüllen, wobei mit gilt. Damit ergibt sich die Anzahl der Möglichkeiten, Ziehungen unter Kugeln mit Zurücklegen ohne Beachtung der Reihenfolge durchzuführen aus
- .
Möchte man ein gegebenes Ergebnis zurück verwandeln in eine echte Ziehung, d. h. in die Anzahl der Ziehungen, die einer beliebigen Kugel angehören, muss man zunächst die Teilmenge in ein Diagramm verwandeln. Dieses Diagramm besteht aus den Zahlen und Strichen. Dabei wird die Teilmenge zunächst sortiert in . Dann wird vor der Zahl ein Strich eingefügt. Die Anzahl der Zahlen zwischen den Strichen sowie vor dem ersten und hinter dem letzten Strich sind die Anzahl der Ziehungen pro Kugel. Dabei wird nicht berücksichtigt. Hat man zum Beispiel für und die Teilmenge gegeben, so ist das Diagramm 1|2|3 4 5. Vor dem ersten Strich steht die 1, zwischen dem ersten und dem zweiten Strich steht die 2 und hinter dem zweiten Strich stehen 3, 4 und 5. Also wurde einmal die erste Kugel gezogen, einmal die zweite Kugel und dreimal die dritte Kugel.
Werden aus der Beispielurne mit sechs Kugeln drei Kugeln mit Zurücklegen ohne Beachtung der Reihenfolge gezogen, dann hat jede zulässige Kugelkombination die Wahrscheinlichkeit
- .
Hier sind mehrfach auftretenden Elemente der Multimenge auch mehrfach notiert und durch Kommas abgetrennt.
Ziehen ohne Zurücklegen ohne Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]
Beim Ziehen ohne Zurücklegen ohne Beachtung der Reihenfolge werden die Ergebnisse ebenfalls durch Teilmengen dargestellt. Konkret heißt dies: Ist wie oben
die Menge der Kugeln, dann ist
die Ergebnismenge für Ziehungen. Man spricht hier auch von einer Kombination ohne Wiederholung. Damit ergibt sich die Anzahl der Möglichkeiten, Ziehungen durchzuführen unter Kugeln ohne Zurücklegen ohne Beachtung der Reihenfolge zu
- .
Werden aus der Beispielurne mit sechs Kugeln drei Kugeln ohne Zurücklegen ohne Beachtung der Reihenfolge gezogen, dann hat jede zulässige Kugelkombination die Wahrscheinlichkeit
- .
Ereignismengen[Bearbeiten | Quelltext bearbeiten]
Einmaliges Ziehen[Bearbeiten | Quelltext bearbeiten]

Ereignisse, etwa dass Kugeln bestimmter Farben gezogen werden, werden in der Wahrscheinlichkeitstheorie ebenfalls durch Mengen dargestellt. Ein Ereignis ist hier einfach eine Teilmenge der Ergebnismenge, also . Beispielsweise wird das Ereignis, dass beim einmaligen Ziehen aus der Beispielurne eine rote oder grüne Kugel gezogen wird, durch
beschrieben. Nach der Laplace-Formel gilt nun für die Wahrscheinlichkeit , dass ein Ereignis eintritt:
- .
Somit lässt sich die Ermittlung der Wahrscheinlichkeit eines Ereignisses auf das Aufzählen von Ergebnissen zurückführen. Beispielsweise ergibt sich als Wahrscheinlichkeit, dass beim einmaligen Ziehen aus der Beispielurne eine rote oder grüne Kugel gezogen wird
- .
Bei mehreren Ziehungen kann allerdings das einzelne Aufzählen von Ergebnissen, etwa mit Hilfe von Baumdiagrammen, sehr aufwändig werden. Stattdessen werden hierfür häufig Hilfsmittel aus der abzählenden Kombinatorik genutzt.
Ziehen gleichfarbiger Kugeln[Bearbeiten | Quelltext bearbeiten]

Zunächst betrachtet man das Ereignis, dass bei Ziehungen immer eine Kugel der gleichen Farbe gezogen wird. Ist die Anzahl der Kugeln dieser Farbe, dann gilt bei einer Ziehung mit Zurücklegen für die Wahrscheinlichkeit dieses Ereignisses
- mit .
Die Wahrscheinlichkeit ist also die -te Potenz der Wahrscheinlichkeit der einmaligen Ziehung einer Kugel dieser Farbe. Bei einer Ziehung ohne Zurücklegen erhält man stattdessen
- .
Für wird diese Wahrscheinlichkeit null, da nicht mehr Kugeln einer Farbe gezogen werden können, als in der Urne vorhanden sind. Beispielsweise beträgt die Wahrscheinlichkeit, dass aus der Beispielurne drei rote Kugeln gezogen werden, bei einer Ziehung mit Zurücklegen
und bei einer Ziehung ohne Zurücklegen
- .
Ziehen mit Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]

Werden verschiedenfarbige Kugeln gezogen, so ist bei der Betrachtung der Ereignisse zu unterscheiden, ob die Reihenfolge, in der die Kugeln gezogen wurden, eine Rolle spielen soll oder nicht. Im ersten Fall spricht man auch von einer geordneten Ziehung, im anderen von einer ungeordneten Ziehung.
Im Folgenden wird der Fall betrachtet, dass pro Farbe genau eine Kugel gezogen wird. Befinden sich in der Urne Kugeln der ersten Farbe, Kugeln der zweiten Farbe und so fort, so beträgt die Wahrscheinlichkeit, dass als erstes eine Kugel der ersten Farbe, als zweites eine Kugel der zweiten Farbe und so weiter bis als letztes eine Kugel der -ten Farbe gezogen wird, bei einer Ziehung mit Zurücklegen
- mit
und bei einer Ziehung ohne Zurücklegen
- .
Beispielsweise beträgt die Wahrscheinlichkeit, dass aus der Beispielurne eine rote, eine grüne und eine blaue Kugel in dieser Reihenfolge gezogen werden, bei einer Ziehung mit Zurücklegen
und bei einer Ziehung ohne Zurücklegen
- .
Genau die gleichen Wahrscheinlichkeiten ergeben sich, wenn eine beliebige andere Reihenfolge der Kugeln (etwa grün, blau, rot) gewählt wird.
Ziehen ohne Beachtung der Reihenfolge[Bearbeiten | Quelltext bearbeiten]

Soll nun die genaue Reihenfolge, in der die Kugeln gezogen werden, außer Acht gelassen werden, müssen zusätzlich alle Permutationen der gezogenen Kugeln berücksichtigt werden. Dadurch ergibt sich als Wahrscheinlichkeit, dass je eine Kugel unterschiedlicher Farbe gezogen wird, bei einer Ziehung mit Zurücklegen
- mit
und bei einer Ziehung ohne Zurücklegen
- .
Beispielsweise beträgt die Wahrscheinlichkeit, dass aus der Beispielurne drei verschiedenfarbige Kugeln gezogen werden, bei einer Ziehung mit Zurücklegen
und bei einer Ziehung ohne Zurücklegen
- .
Im allgemeineren Fall, dass mehrere Kugeln jeder Farbe gezogen werden, müssen Permutationen mit Wiederholung betrachtet werden. Die Anzahl solcher Permutationen wird durch Multinomialkoeffizienten angegeben, siehe den Abschnitt Anzahl der Kugeln einer Farbkombination.
Bei einer Ziehung ohne Zurücklegen ist auch eine Uminterpretation der Wahrscheinlichkeit in einem reduzierten Wahrscheinlichkeitsraum mit Elementen möglich. In diesem Wahrscheinlichkeitsraum werden Ergebnisse als äquivalent angesehen, wenn sie durch Permutation der Kugeln auseinander hervorgehen. Man spricht hier auch von einer Kombination ohne Wiederholung. Auch in dem reduzierten Wahrscheinlichkeitsraum sind alle Ergebnisse gleich wahrscheinlich.
Eine solche Uminterpretation ist ebenso bei einer Ziehung mit Zurücklegen möglich und man erhält dann einen reduzierten Wahrscheinlichkeitsraum mit Elementen. Entsprechend spricht man hier von einer Kombination mit Wiederholung. Allerdings ist dieser Wahrscheinlichkeitsraum kein Laplace-Raum mehr, denn die Wahrscheinlichkeit, dass zwei verschiedene Kugeln gezogen werden, ist hier doppelt so hoch wie diejenige für zwei gleiche Kugeln.
Zusammenfassung von Ereignissen[Bearbeiten | Quelltext bearbeiten]
Komplexere Ereignisse können häufig in einfachere, sich wechselseitig ausschließende Ereignisse zerlegt werden. Ist eine Ereignismenge die Vereinigung paarweise disjunkter Ereignisse , dann ist die Wahrscheinlichkeit des Gesamtereignisses die Summe der Wahrscheinlichkeiten der einzelnen Ereignisse:
- .
Beispielsweise beträgt die Wahrscheinlichkeit, dass aus der Beispielurne zweimal eine Kugel der gleichen Farbe gezogen wird, bei einer Ziehung ohne Zurücklegen
- .
Gelegentlich ist es auch effizienter, die nicht eingetretenen Ergebnisse aufzuzählen, wobei man die Formel für die Gegenwahrscheinlichkeit nutzt:
Beispielsweise beträgt die Wahrscheinlichkeit, dass aus der Beispielurne bei zweimal Ziehen ohne Zurücklegen keine grüne Kugel gezogen wird
- .
Abgeleitete Verteilungen[Bearbeiten | Quelltext bearbeiten]
Ereignissen zugeordnete Größen, wie die Anzahl gezogener Kugeln einer bestimmten Farbe oder die Anzahl der Ziehungen, bis das erste Mal eine Kugel einer bestimmten Farbe gezogen wird, können als diskrete Zufallsvariablen interpretiert werden. Typischerweise ist die Wahrscheinlichkeitsverteilung solcher Zufallsvariablen nicht mehr gleichverteilt, das heißt, die Werte, die die Zufallsvariable annehmen kann, haben nicht mehr die gleiche Wahrscheinlichkeit. Einige solcher durch Urnenmodelle induzierter Wahrscheinlichkeitsverteilungen besitzen in der Statistik eine große Bedeutung und haben eigene Namen.
Anzahl der Kugeln einer Farbe[Bearbeiten | Quelltext bearbeiten]

In der Urne befinden sich Kugeln einer Farbe und Kugeln anderer Farben. Die Wahrscheinlichkeit, dass nach Ziehungen genau Kugeln der ersten Farbe gezogen wurden, ist bei einer Ziehung mit Zurücklegen
- mit .
Die entsprechende Wahrscheinlichkeitsverteilung heißt Binomialverteilung, bei einer einmaligen Ziehung auch Bernoulli-Verteilung. Bei einer Ziehung ohne Zurücklegen ergibt sich analog
und die entsprechende Verteilung wird hypergeometrische Verteilung genannt.
Wartezeit für eine Anzahl von Kugeln einer Farbe[Bearbeiten | Quelltext bearbeiten]
In der Urne befinden sich wieder Kugeln einer Farbe und Kugeln anderer Farben. Die Wahrscheinlichkeit, dass nach Ziehungen im letzten Zug eine Kugel der ersten Farbe das -te Mal gezogen wurde, ist bei einer Ziehung mit Zurücklegen
- mit .
Die entsprechende Wahrscheinlichkeitsverteilung heißt negative Binomialverteilung und im Spezialfall geometrische Verteilung. Bei einer Ziehung ohne Zurücklegen ergibt sich analog
und die entsprechende Verteilung wird negative hypergeometrische Verteilung genannt.
Anzahl der Kugeln einer Farbkombination[Bearbeiten | Quelltext bearbeiten]
In der Urne befinden sich nun Kugeln der Farbe , . Die Wahrscheinlichkeit, dass nach Ziehungen genau Kugeln der Farbe für gezogen wurden, ist bei einer Ziehung mit Zurücklegen:
- mit .
Die entsprechende Wahrscheinlichkeitsverteilung heißt Multinomialverteilung. Bei einer Ziehung ohne Zurücklegen ergibt sich analog
und die entsprechende Verteilung wird multivariate hypergeometrische Verteilung genannt.
Modellvarianten[Bearbeiten | Quelltext bearbeiten]

Bei einem Pólya-Urnenmodell, benannt nach dem ungarischen Mathematiker George Pólya, wird nach dem Ziehen einer Kugel neben der Kugel selbst zusätzlich eine exakte Kopie der Kugel in die Urne gelegt. Die Anzahl der Kugeln in der Urne wächst dadurch mit jeder Ziehung um eins an. Auf gewisse Weise kann ein Pólya-Urnenmodell als das Gegenteil einer Ziehung ohne Zurücklegen angesehen werden. Nachdem Kugeln in einer häufig vorkommenden Farbe im Laufe der Ziehungen noch häufiger werden, können durch Pólya-Urnenmodelle selbstverstärkende Effekte modelliert werden. Eine wichtige, durch das Pólya-Urnenmodell ableitbare Wahrscheinlichkeitsverteilung ist die Beta-Binomialverteilung.
Für Pólya-Urnenmodelle gibt es eine Reihe von Verallgemeinerungen, beispielsweise indem nicht nur eine, sondern mehrere Kopien der gezogenen Kugel in die Urne gelegt werden. In weiteren Varianten wird statt der gezogenen Kugel eine Kopie einer andersfarbigen Kugel in die Urne zurückgelegt oder zusätzlich zurückgelegt.[4]
Eine weitere Verallgemeinerung besteht in der Verwendung mehrerer Urnen, die alle mit Kugeln gefüllt sind. Eine Ziehung erfolgt dann in zwei Schritten: im ersten Schritt wird zufällig eine der Urnen ausgewählt und im zweiten Schritt dann aus der ausgewählten Urne eine Kugel gezogen. Auf gewisse Weise dual dazu sind Fragestellungen bezüglich der Belegung der Urnen, wenn Kugeln nicht gezogen, sondern zufällig auf die verfügbaren Urnen verteilt werden, siehe Abzählende Kombinatorik#Bälle und Fächer.[5]
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Urnenmodelle stehen stellvertretend für eine große Klasse von Zufallsexperimenten, wobei Urne und Kugeln durch andere Objekte entsprechend ersetzt werden. Beispiele sind:
- das Werfen einer Münze oder eines Würfels
- das Geben der Spielkarten eines Kartenspiels
- die Ziehung der Lottozahlen oder andere Lotterien
- die Durchführung von Glücksspielen, beispielsweise Roulette
Urnenmodelle helfen unter anderem beim Verständnis folgender Phänomene und Probleme:
- Geburtstagsparadoxon
- In einer Klasse mit 23 Schülern haben mit einer Wahrscheinlichkeit von über 50 % zwei am gleichen Tag Geburtstag.
- Ellsberg-Paradoxon
- Bei menschlichen Entscheidungen wird ein Risiko eher in Kauf genommen als Ungewissheit.
- Sankt-Petersburg-Paradoxon
- Bei einem Glücksspiel mit unendlich großer erwarteter Auszahlung kann die subjektive Gewinnerwartung dennoch gering sein.
- Sammelbilderproblem
- Wie viele zufällig gezogene Sammelbilder sind im Durchschnitt nötig, um eine vollständige Sammlung zu erhalten?
Anwendungen von Urnenmodellen sind beispielsweise:
- die Durchführung zufälliger Stichproben in der Qualitätskontrolle
- die Bestimmung der Ausfallwahrscheinlichkeit technischer Systeme mit mehreren Komponenten
- das Auftreten von Versicherungsfällen in einer Versicherung
- die Modellierung von Diffusionsvorgängen mit dem Ehrenfest-Modell
- das Pólya-Urnenmodell zur Modellierung von Infektionsgeschehen.
In der Physik[Bearbeiten | Quelltext bearbeiten]
Urnenmodelle finden in der statistischen Physik Anwendung. Die Kugeln sind hier z. B. Gasmoleküle, Protonen, Elektronen usw. und der Phasenraum wird in Zellen (Fächer/Urnen) unterteilt. Abhängig davon, welche Annahme über die Gleichverteilung gemacht wird, erhält man verschiedene, aus der Erfahrung heraus begründbare Verteilungen, die „Statistiken“ genannt werden. Bei der Maxwell-Boltzmann-Statistik, die in der kinetischen Gastheorie eine große Rolle spielt, tritt etwa ein Modell auf, in dem die Teilchen (Kugeln) unterscheidbar sind und Mehrfachbesetzungen (im in Zellen unterteilten Phasenraum) erlaubt. Das Urnenmodell, bei dem die Teilchen nicht unterscheidbar und Mehrfachbesetzungen erlaubt sind, führt zur Bose-Einstein-Statistik[6] und wird u. a. für Photonen verwendet. Das Urnenmodell, bei dem die Teilchen nicht unterscheidbar sind und es keine Mehrfachbesetzungen gibt, führt zur Fermi-Dirac-Statistik[7] und wird u. a. für Elektronen, Neutronen und Protonen verwendet. Die Bedingung, dass höchstens ein Teilchen in einer Zelle liegt, ist analog zum Pauli-Verbot zu verstehen.[8]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Karl Bosch: Elementare Einführung in die Wahrscheinlichkeitsrechnung. 11. Auflage. Vieweg, 2011, ISBN 978-3-8348-8331-5, S. 12–91.
- Hans-Otto Georgii: Stochastik: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. de Gruyter, 2009, ISBN 978-3-11-021526-7, S. 29–39.
- Norbert Henze: Stochastik für Einsteiger. 10. Auflage. Springer, 2013, ISBN 978-3-658-03076-6, S. 62–65 (Auszug bei Google Books).
- Herbert Kütting, Martin J. Sauer: Elementare Stochastik. 3. Auflage. Springer Spektrum, 2011, ISBN 978-3-8274-2759-5, S. 138–152.
- Norman L. Johnson, Samuel Kotz: Urn Models and their Application. John Wiley & Sons, 1977, ISBN 0-471-44630-0.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- A.V. Prokhorov: Urn model. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- Eric W. Weisstein: Ball Picking. In: MathWorld (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Samuel Kotz, N. Balakrishnan: Advances in Urn Models in the Past Two Decades. In: Advances in Combinatorial Methods and Applications to Probability and Statistics (= Statistics for Industry and Technology). Springer, 1997, S. 204.
- ↑ Jakob Bernoulli: Wahrscheinlichkeitsrechnung (Ars conjectandi), Dritter und vierter Theil (= Ostwalds Klassiker der exakten Wissenschaften). Engelmann, Leipzig 1899 (übersetzt und herausgegeben von R. Haussner).
- ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application. John Wiley & Sons, 1977, S. 22.
- ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application. John Wiley & Sons, 1977, S. 177.
- ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application. John Wiley & Sons, 1977, S. 107 ff.
- ↑ Marcelo Alonso, Edward J. Finn: Fundamental University Physics, Vol.3, Quantum and Statistical Physics. Addison-Wesley Publishing Company, 1968, S. 529.
- ↑ Marcelo Alonso, Edward J. Finn: Fundamental University Physics, Vol.3, Quantum and Statistical Physics. Addison-Wesley Publishing Company, 1968, S. 520.
- ↑ Norbert Henze: Stochastik: Eine Einführung mit Grundzügen der Maßtheorie. Springer, 2019, ISBN 978-3-662-59562-6, S. 37.



























































































