Negative Binomialverteilung
| Negative Binomialverteilung | |
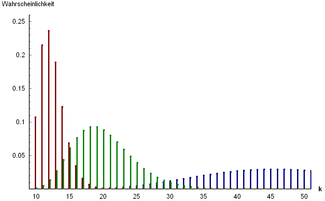
Wahrscheinlichkeitsfunktion  Wahrscheinlichkeitsverteilung der Variante B. In diesem Beispiel ist Parameter von abhängig, sodass gilt (das erfordert ). Der Erwartungswert ist als orange Linie dargestellt; die Standardabweichung als grüne. | |
| Verteilungsfunktion | |
| Parameter | r > 0 – Anzahl Erfolge bis zum Abbruch p ∈ (0,1) – Einzel-Erfolgs-Wahrscheinlichkeit |
|---|---|
| Träger | k ∈ { 0, 1, 2, 3, … } – Anzahl Misserfolge |
| Wahrscheinlichkeitsfunktion | |
| Verteilungsfunktion | Eulersche Betafunktion |
| Erwartungswert | |
| Modus | |
| Varianz | |
| Schiefe | |
| Wölbung | |
| Momenterzeugende Funktion | |
| Charakteristische Funktion | |
Die negative Binomialverteilung (auch Pascal-Verteilung) ist eine univariate Wahrscheinlichkeitsverteilung. Sie zählt zu den diskreten Wahrscheinlichkeitsverteilungen und ist eine der drei Panjer-Verteilungen.
Sie beschreibt die Wahrscheinlichkeit, dass in einem Bernoulli-Prozess nach k Misserfolgen genau r Erfolge eingetreten sind.
Neben der Poisson-Verteilung ist die negative Binomialverteilung die wichtigste Schadenzahlverteilung in der Versicherungsmathematik. Dort wird sie insbesondere als Schadenzahlverteilung in der Krankenversicherung benutzt, seltener im Bereich Kraftfahrzeug-Haftpflicht oder Kasko.
Herleitung der negativen Binomialverteilung[Bearbeiten | Quelltext bearbeiten]
Man kann diese Verteilung mit Hilfe des Urnenmodells mit Zurücklegen beschreiben: In einer Urne befinden sich zwei Sorten Kugeln (dichotome Grundgesamtheit). Der Anteil der Kugeln erster Sorte beträgt . Die Wahrscheinlichkeit, dass eine Kugel erster Sorte gezogen wird, beträgt also .
Es wird nun so lange eine Kugel gezogen und wieder zurückgelegt, bis erstmals genau Kugeln erster Sorte resultieren. Man kann eine Zufallsvariable : „Zahl der Versuche, bis erstmals Erfolge resultieren“ definieren. Die Zahl der Versuche liegt in der Menge . hat abzählbar unendlich viele mögliche Ausprägungen.
Die Wahrscheinlichkeit, dass Versuche nötig waren, um Erfolge zu erzielen, also , berechnet man nach folgender Überlegung:
Es sollen zum jetzigen Zeitpunkt bereits Versuche stattgefunden haben. Es wurden insgesamt Kugeln erster Sorte gezogen. Die Wahrscheinlichkeit dafür wird durch die Binomialverteilung der Zufallsvariablen : „Zahl der Kugeln erster Sorte bei Versuchen“ angegeben:
Die Wahrscheinlichkeit, dass nun eine weitere Kugel erster Sorte gezogen wird, ist dann
Eine Zufallsvariable heißt damit negativ binomialverteilt mit den Parametern (Anzahl der erfolgreichen Versuche) und (Wahrscheinlichkeit des Eintretens eines Erfolges im Einzelversuch), wenn sich für sie die Wahrscheinlichkeitsfunktion
angeben lässt.
Diese Variante wird hier Variante A genannt, um Verwechslungen vorzubeugen.
Alternative Definition[Bearbeiten | Quelltext bearbeiten]
Eine diskrete Zufallsgröße unterliegt der negativen Binomialverteilung mit den Parametern und , wenn sie die Wahrscheinlichkeiten
für besitzt.
Beide Definitionen stehen über in Beziehung; während die erste Definition also nach der Anzahl der Versuche (erfolgreiche und erfolglose) bis zum Eintreten des -ten Erfolgs fragt, interessiert sich die alternative Darstellung für die Anzahl der Misserfolge bis zum Eintreten des -ten Erfolgs. Dabei werden die Erfolge nicht mitgezählt. Die Zufallsvariable bezeichnet dann nur die Anzahl der misslungenen Versuche.
Diese Variante wird hier Variante B genannt.
Eigenschaften der negativen Binomialverteilung[Bearbeiten | Quelltext bearbeiten]
Erwartungswert[Bearbeiten | Quelltext bearbeiten]
- Variante A
Der Erwartungswert bestimmt sich zu
- .
- Variante B
Bei der alternativen Definition ist der Erwartungswert um kleiner, also
- .
Varianz[Bearbeiten | Quelltext bearbeiten]
Die Varianz der negativen Binomialverteilung ist für beide Definitionen gegeben durch
- .
Die Varianz ist bei der alternativen Definition immer größer als der Erwartungswert (Überdispersion).
Variationskoeffizient[Bearbeiten | Quelltext bearbeiten]
- Variante A
Aus Erwartungswert und Varianz ergibt sich sofort der Variationskoeffizient zu
- Variante B
In der alternativen Darstellung ergibt sich
- .
Schiefe[Bearbeiten | Quelltext bearbeiten]
Die Schiefe ergibt sich für beide Varianten zu:
- .
Wölbung[Bearbeiten | Quelltext bearbeiten]
Der Exzess ist für beide Varianten
- .
Damit ist dann die Wölbung
- .
Charakteristische Funktion[Bearbeiten | Quelltext bearbeiten]
- Variante A
Die charakteristische Funktion hat die Form
- .
- Variante B
Alternativ ergibt sich
- .
Wahrscheinlichkeitserzeugende Funktion[Bearbeiten | Quelltext bearbeiten]
- Variante A
Für die wahrscheinlichkeitserzeugende Funktion erhält man
- mit .
- Variante B
Analog ist dann
- .
Momenterzeugende Funktion[Bearbeiten | Quelltext bearbeiten]
- Variante A
Die momenterzeugende Funktion der negativen Binomialverteilung ist
- mit .
- Variante B
Dann ist die Alternativdarstellung
Summen von negativ binomialverteilten Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Sind zwei unabhängige negativ binomialverteilte Zufallsvariablen zu den Parametern und . Dann ist wieder negativ binomialverteilt zum Parameter und . Die negative Binomialverteilung ist also reproduktiv, für die Faltung gilt ,
sie bildet eine Faltungshalbgruppe.
Verallgemeinerung auf reelle Parameter[Bearbeiten | Quelltext bearbeiten]
Die obige Herleitung und Interpretation der negativen Binomialverteilung über das Urnenmodell ist nur für möglich. Es existiert jedoch auch eine Verallgemeinerung der negativen Binomialverteilung für . Dazu wird eine Poisson-Verteilung betrachtet, deren Intensität zufällig gemäß einer Gamma-Verteilung mit den Parametern und verteilt ist. Wird nun die Mischverteilung dieser beiden Verteilungen gebildet, ergibt sich die sogenannte Poisson-Gamma-Verteilung. Für die Wahrscheinlichkeitsfunktion dieser Verteilung gilt dann
Für ergibt sich gerade die Wahrscheinlichkeitsfunktion der negativen Binomialverteilung. Somit lässt sich die negative Binomialverteilung auch für sinnvoll interpretieren. Die Wahrscheinlichkeit, Erfolge zu erreichen, ist dann gleich der Wahrscheinlichkeit, bei einer Binomialverteilung mit zufälligem, gammaverteilten Parameter Erfolge zu erreichen. Die Gamma-Funktionen in der Wahrscheinlichkeitsfunktion können auch durch verallgemeinerte Binomialkoeffizienten ersetzt werden.
Diese Konstruktion entspricht der oben definierten Variante B. Alle Charakteristika, wie Erwartungswert, Varianz und so weiter, bleiben unverändert gültig. Zudem ist die Variante für reelles unendlich teilbar.
Beziehungen zu anderen Verteilungen[Bearbeiten | Quelltext bearbeiten]
Beziehung zur Binomialverteilung[Bearbeiten | Quelltext bearbeiten]
In der Tabelle wird die Beziehung zur Binomialverteilung veranschaulicht:
| Deterministisch | Zufällig | Fragestellung | |
|---|---|---|---|
| Binomialverteilung | Versuche | Erfolge | Wie viele Erfolge haben wir in Versuchen? |
| Negative Binomialverteilung | Erfolge | Versuche | Wie viele Versuche sind erforderlich, um Erfolge zu haben? |
Beziehung zur geometrischen Verteilung[Bearbeiten | Quelltext bearbeiten]
Die negative Binomialverteilung geht für in die geometrische Verteilung über. Andererseits ist Summe voneinander unabhängiger geometrisch verteilter Zufallsgrößen mit demselben Parameter negativ-binomialverteilt mit den Parametern und . Allerdings ist auch hier zu beachten, welche Parametrisierungsvariante gewählt wurde. Als Summe unabhängiger, identisch verteilter Zufallsvariablen ist für große annähernd normalverteilt.
Beziehung zur zusammengesetzten Poisson-Verteilung[Bearbeiten | Quelltext bearbeiten]
Die negative Binomialverteilung entsteht aus der zusammengesetzten Poisson-Verteilung, wenn man diese mit der logarithmischen Verteilung kombiniert. Die Parameter gehen in die Variante B über mit und .
Beispiel[Bearbeiten | Quelltext bearbeiten]

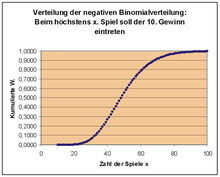
Die Studentin Paula spielt heute Abend Skat. Aus langer Erfahrung weiß sie, dass sie bei jedem 5. Spiel gewinnt. Gewinnen ist folgendermaßen definiert: Sie muss zunächst ein Spiel durch Reizen bekommen, dann muss sie dieses Spiel gewinnen.
Da sie morgen um acht Uhr Statistik-Vorlesung hat, soll der Abend nicht zu lang werden. Deshalb hat sie beschlossen, nach dem 10. gewonnenen Spiel nach Hause zu gehen. Nehmen wir an, dass ein Spiel etwa 4 Minuten dauert (großzügig gerechnet). Mit welcher Wahrscheinlichkeit kann sie nach zwei Stunden nach Hause gehen, also nach 30 Spielen?
Wir gehen mit unseren Überlegungen analog zu oben vor:
Mit welcher Wahrscheinlichkeit hat sie in 29 Spielen 9-mal gewonnen? Wir berechnen diese Wahrscheinlichkeit mit der Binomialverteilung, in Begriffen des Urnenmodells bei 29 Versuchen und 9 Kugeln erster Sorte:
Die Wahrscheinlichkeit, den 10. Gewinn beim 30. Spiel zu machen, ist nun
Diese Wahrscheinlichkeit scheint nun sehr klein zu sein. Die Grafik der negativ binomialverteilten Zufallsvariablen zeigt, dass insgesamt die Wahrscheinlichkeiten sehr klein bleiben. Wie soll da die arme Paula jemals ins Bett kommen? Wir können sie beruhigen: Es genügt ja, danach zu fragen, wie viele Versuche Paula höchstens braucht, es müssen ja nicht genau 30 sein.
Die Wahrscheinlichkeit, dass höchstens 30 Versuche nötig sind, ist die Verteilungsfunktion der negativen Binomialverteilung an der Stelle , was hier die Summe der Wahrscheinlichkeiten ergibt. Ein Blick auf die Grafik der Verteilungsfunktion zeigt: Wenn Paula mit einer 50%igen Wahrscheinlichkeit zufrieden ist, müsste sie höchstens ca. 50 Spiele absolvieren, das wären 50·4 min = 200 min = 3h 20 min. Um mit einer 80%igen Wahrscheinlichkeit ihre 10 Gewinne zu bekommen, müsste sie höchstens ca. 70 Spiele spielen, also knapp 5 Stunden. Vielleicht sollte Paula doch ihre Strategie der Spielezahl ändern.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- A.V. Prokhorov: Negative binomial distribution. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- Eric W. Weisstein: Negative Binomial Distribution. In: MathWorld (englisch).
Literatur[Bearbeiten | Quelltext bearbeiten]
- Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6, doi:10.1007/978-3-642-36018-3.
- Christian Hesse: Angewandte Wahrscheinlichkeitstheorie. 1. Auflage. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2, doi:10.1007/978-3-663-01244-3.


![{\displaystyle E[X]=10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0185efa6b5485f8bce9ca2b21f4ebeaeff8ae78c)























































![{\displaystyle {\begin{aligned}f(k|r,p)&=\int _{0}^{\infty }f_{\text{Poi}}(k|\lambda )\cdot f_{\text{Gamma}}(\lambda |r,{\frac {p}{1-p}})\;\mathrm {d} \lambda \\[8pt]&=\int _{0}^{\infty }{\frac {\lambda ^{k}}{k!}}e^{-\lambda }\cdot \lambda ^{r-1}{\frac {e^{-\lambda p/(1-p)}}{{\big (}{\frac {1-p}{p}}{\big )}^{r}\,\Gamma (r)}}\;\mathrm {d} \lambda \\[8pt]&={\frac {p^{r}(1-p)^{-r}}{k!\,\Gamma (r)}}\int _{0}^{\infty }\lambda ^{r+k-1}e^{-\lambda /(1-p)}\;\mathrm {d} \lambda \\[8pt]&={\frac {(p)^{r}(1-p)^{-r}}{k!\,\Gamma (r)}}\ (1-p)^{r+k}\,\Gamma (r+k)\\[8pt]&={\frac {\Gamma (r+k)}{k!\;\Gamma (r)}}\;(1-p)^{k}p^{r}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164b4691984d59427ac464e5ffaf363a77ffe8c7)












