Benutzer:Schwatzwutz/Küche

https://en.wikipedia.org/w/index.php?title=0.999...&oldid=576300590

0.999...

In der Mathematik bezeichnet der Dezimalbruch 0.999... (auch mit mehr oder weniger 9en vor der Ellipse, 0.(9) oder 0.9) die reelle Zahl Eins. Beweise dieser Gleichheit wurden mit verschieden starker mathematischer Strenge formuliert, je nach verwendeter Grundlage der reellen Zahlen, Startannahmen, historischem Kontext und Zielgruppe.

Zu jeder terminierenden Dezimalzahl findet sich eine äquivalente Darstellung mit unendlich vielen 9en, wie z. B. 8.32 und 8.31999... Die terminierende dezimale Darstellung wird dabei meistens bevorzugt, was zu dem Misverständnis beiträgt, es gebe nur diese eine. Dasselbe Phänomen tritt auch in allen anderen Stellenwertsystemen auf.

Die Gleichheit von 0.999... und 1 ist nah verwandt mit der Nichtexistenz von Infinitesimalzahlen innerhalb der reellen Zahlen. In alternativen Zahlenmengen wie den hyperreellen Zahlen, treten Infinitesimalzahlen auf. Solche Mengen lassen im Gegensatz zu den reellen Zahlen einen Unterschied zwischen den Symbolen 1 und 0.999... zu, da letzteres dort so interpretiert wird, dass es infinitesimal kleiner ist als 1.

Die Gleichheit 0.999... = 1 ist seit langem in der Mathematik akzeptiert und ein Teil des mathematischen Unterrichts. Nichtsdestotrotz empfinden es viele Schüler als hinreichend kontraintuitiv, um es anzuzweifeln oder abzulehnen. Somit ist die Schwierigkeit sie davon zu überzeugen Untersuchungsgegenstand vieler Studien der mathematischen Pädagogik.

Algebraische Beweise

Algebraische Beweise, die zeigen, dass 0.999... die Zahl 1 repräsentiert benutzen Brüche, schriftliche Division und Ziffermanipulation, um Transformationen zu konstruieren, die die Gleichheit erhalten.

Brüche und schriftliche Division

Unendliche Dezimalstellen sind ein notwendiges Konzept, um rationale Zahlen (Brüche) darzustellen. Mit simpler schriftlicher Division zweier Zahlen wie 1/9 entsteht eine sich wiederholende Dezimalzahl, 0.111..., in der die 1 als Nachkommastelle unendlich oft wiederkehrt. Dadurch ergibt sich leicht ein Beweis der Gleicheit von 0.999... und 1.

${\begin{aligned}{\frac {1}{9}}&=0.111\dots \\9\times {\frac {1}{9}}&=9\times 0.111\dots \\1&=0.999\dots \end{aligned}}$

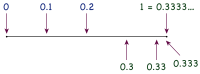
Alternativ kann 1/3 = 0.333 mit 3 multipliziert werden.

Diskussion

Der Grad, zu dem diese Art von Beweisen ausreicht, hängt von der Zielgruppe ab. In einführender Arithmetik erklärt er zwar die Gleichheit 0.999... = 1, nicht jedoch die Ungleichung 0.888... < 0.89. Anfängern in Algebra, hilft er die Frage zu beantworten, warum zwischen Brüchen und Dezimalzahlen umgerechnet werden kann. Allerdings lässt er die fundamentale Beziehung zwischen Dezimaldarstellungen und den Zahlen, die sie repräsentieren erahnen, was der Frage zugrunde liegt, warum zwei verschiedene Dezimaldarstellungen überhaupt gleich sein können.

Sobald ein Repräsentatsschema definiert ist, können die Regeln der dezimalen Arithmetik, wie sie oben benutzt wurden, gerechtfertigt werden. Damit kann im Folgenden direkt gezeigt werden, dass 0.999... und 1.000... die gleiche Zahl repräsentieren.

Analytische Beweise

Da die Frage nach der 0.999... nicht die formale Herleitung der Mathematik betrifft, kann sie verschoben werden, bis die Standardsätze der reellen Analysis bewiesen werden. Eine Vorraussetzung ist, die reellen Zahlen zu charakterisieren, die durch Dezimaldarstellungen repräsentiert werden können. Letztere bestehen aus einer ganzen Zahl, einem Komma und Nachkommastellen, die den Bruch darstellen. Um 0.999... zu untersuchen, kann der ganzzahlige Teil als b₀ zusammengefasst und Vorzeichen vernachlässigt werden. Eine Dezimalrepräsentation hat also die Form:$b_{0}.b_{1}b_{2}b_{3}b_{4}b_{5}\dots$

Hierbei sind die Nachkommastellen nicht auf eine endliche Zahl von Ziffern begrenzt. Dies ist ein Stellenwertsystem. Beispielsweise trägt die Ziffer 5 in 500 zehn mal mehr bei als die 5 in 50 und die 5 in 0.05 ein Zehntel so viel wie die 5 in 0.5 (,da sie eine andere Stelle einnimmt).

Unendliche Reihen und Folgen

Die wohl bekannteste Herleitung der Dezimalentwicklung ist, sie über die Summe einer unendlichen Reihe zu definieren:$b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}\left({\tfrac {1}{10}}\right)+b_{2}\left({\tfrac {1}{10}}\right)^{2}+b_{3}\left({\tfrac {1}{10}}\right)^{3}+b_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots .$

Im Fall der 0.999... kann die Konvergenz der geometrischen Reihe genutzt werden:

Wenn $|r|<1\,\!$ dann gilt $ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.$

Weil 0.999... genau dieser Summe mit r = 1/10 entspricht, beantwortet der Satz die Eingangsfrage:$0.999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1.\,$

Dieser Beweis (urprünglich: 10 = 9.999...) erschien bereits 1770 in Leonhard Euler's vollständigen Anleitung zur Algebra.

Limits: Das Einheitsintervall im quaternären System (Basis 4) mit der Folge der Brüche (0.3, 0.33, 0.333, ...), die zu 1 konvergiert.

Die Summe der geometrischen Reihe selbst wurde schon vor Euler entdeckt. Eine typische Herleitung des 18. Jahrhunderts nutzte eine Termmanipulation ähnlich dem algebraischen Beweis (s.o.). Noch 1811 wurde ein solches Argument von dem Mathematiker Bonnycastle in seiner Introduction to Algebra verwendet, um ebendiese Aussage über 0.999... zu treffen. Eine Reaktion des 19. Jahrhunderts auf diesen freien Umgang mit Reihen stellte die Definition dar, die noch heute gilt: Die Summe einer Reihe ist als Grenzwert der Folge ihrer Partialsummen definiert. Ein entsprechender Beweis berechnet explizit diese Folge, er findet sich in jeder beweisbasierten Einführung in die Analysis.

Eine Folge (x₀, x₁, x₂, ...) hat einen Grenzwert, wenn der Unterschied |x − x_n| für hinreichend große n beliebig klein wird. Die Behauptung 0.999...=1 kann über den Grenzwert einer Folge bewiesen werden:</ref>

$0.999\ldots =\lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1.\,$

Der letzte Schritt, dass 1/(10^n) gegen Null geht für n gegen Unendlich, wird oft mit dem archimedischen Axiom der reellen Zahlen begründet. Diese Sichtweise von 0.999... als Grenzwert wird oft in einer plastischeren Weise, wenn auch ungenauer, ausgedrückt. Beispielsweise beschreibt das Lehrbuch The University Arithmetic von 1846, dass "0.999... im Unendlichen gegen 1 geht, weil jedes Anfügen einer weitern 9, den Unterschied zu 1 verringert"; in der Arithmetic for Schools von 1895 heißt es:"Wenn man eine große Anzahl an 9en nimmt, wird die Differenz zwischen 1 und 0.99999 [...] unfassbar klein". Solche Näherungsverfahren (Heuristiken) werden oft von Schülern so aufgefasst, als sei 0.999... kleiner als 1.

Intervallschachtelung und Supremum

→ Hauptartikel: Intervallschachtelung

Intervallschachtelung zur Basis 3: 1 = 1.000... = 0.222...

Die Reihendefinition (s.o.) ist ein einfacher Weg, die reelle Zahl zu definieren, die durch eine Dezimaldarstellung benannt wird. Andersherum kann man nach der Dezimalrepräsentation suchen, die eine gegebene Zahl definiert.

Wenn eine reelle Zahl x z. B. in einem geschlossenem Intervall [0, 10] liegt, ist sie größer als oder genau 0 und kleiner als oder genau 10. Ein solches Intervall kann in zehn Teile zerlegt werden, die sich nur an den Enden überlappen: [0, 1], [1, 2], [2, 3], ... [9, 10]. Die Zahl x muss in einem dieser Teilintervalle liegen. Liegt sie beispielsweise in [2, 3], dann nimmt man dieses Intervall, merkt die Ziffer 2 und teilt es wiederum in zehn Intervalle auf: [2, 2.1], [2.1, 2.2], ..., [2.8, 2.9], [2.9, 3]. Führt man diesen Prozess der Intervallschachtelung fort, erhält man eine unendliche Folge von ineinander geschaltelten Intervallen, die durch eine unendliche Folge von Ziffern b₀, b₁, b₂, b₃, ... benannt werden. Man schreibt

$x=b_{0}.b_{1}b_{2}b_{3}\dots$.

In diesem Formalismus geben die Gleichheiten 1 = 0.999... und 1 = 1.000... wieder, dass 1 sowohl in dem Intervall [0, 1] als auch in [1, 2] liegt, man kann sowohl das eine Subintervall als auch das andere wählen, wenn man auf die jeweilige Ziffer stößt. Um sicher zu gehen, dass diese Notation das Gleichheitszeichen berücksichtigt, braucht es einen Weg, eine eindeutige reelle Zahl zu jeder Dezimaldarstellung zu finden. Dies kann mit Grenzwerten sichergestellt werden, andere Konstruktionen behalten jedoch den Intervallansatz bei.

Ein praktischer Weg ist der Satz über Intervallschachtelungen, der garantiert, dass in dem Schnitt einer Intervallschachtelung von geschlossenen Intervallen, deren Längen beliebig klein werden, nur eine einzige reelle Zahl liegt. Nun ist b₀.b₁b₂b₃... die eindeutige gesuchte Zahl, die in allen Intervallen [0, 1], [0.9, 1], [0.99, 1] und [0.99...9, 1] (für beliebig viele 9en) liegt. Da 1 bereits ein Element all dieser Intervalle ist, folgt: 0.999... = 1.

Der Satz über die geschachtelten Intervalle ist auf einer fundamentalen Eigenschaft der reellen Zahlen begründet: der Existenz von kleinsten oberen Schranken (Suprema). Um dies direkt zu nutzen, kann man b₀.b₁b₂b₃... als kleinste obere Schranke der Menge der Annäherungen {b₀, b₀.b₁, b₀.b₁b₂, ...} definieren. Es kann gezeigt werden, dass diese Definition mit dem Prozess des Unterteilens übereinstimmt, woraus abermals 0.999... = 1 folgt. Tom Apostol schließt:

„Die Tatsache, dass eine reelle Zahl zwei verschiedene dezimale Repräsentation hat, spiegelt die Tatsache wieder, dass zwei verschiedene Mengen reeller Zahlen das gleiche Supremum aufweisen können.“

– Tom Apostol: Mathematical analysis

Beweise über die Konstruktion der reellen Zahlen

Die reellen Zahlen können über die Mengentheorie eplizit als Struktur definiert werden, die auf den rationalen Zahlen aufbaut. Die natürlichen Zahlen - 0, 1, 2, 3, ... - beginnen mit 0 und laufen aufsteigend fort, sodass jede Zahl einen Nachfolger hat. Über den jeweiligen negativen Partner kann man die natürlichen zu den ganzen und über Brüche zu den rationalen Zahlen erweitern. Diese Zahlensysteme werden von der Arithmetik der Addition, Subtraktion, Multiplikation und Division begleitet. Darüber hinaus enthalten sie Ordnung, sodass eine Zahl mit einer anderen verglichen werden kann und entweder größer oder kleiner als oder gleich dieser Zahl ist.

Der Schritt von den rationalen Zahlen zu den reellen ist ein großer. Zwei populäre Wege, diesen Schritt zu machen, wurden 1872 veröffentlicht: Dedekindschnitte und Cauchyfolgen. Beweise, dass 0.999...=1, die diese Konstruktionen direkt nutzen, finden sich in modernen Lehrbüchern der Analysis nicht, da die Analysis meist axiomatisch eingeführt wird und im Fall, dass eine solche Konstruktion vorliegt, werden meist die Axiome der reellen Zahlen gezeigt, um damit die oben genannten Beweise zu unterstützen. Mehrere Autoren argumentieren jedoch, dass solche Beweise, die direkt mit der Konstruktion der reellen Zahlen beginnen, in sich geschlossener sind.

Dedekind-Schnitte

→ Hauptartikel: Dedekindscher Schnitt

Jede reelle Zahl x kann als unendliche Menge aufgefasst werden, bestehend aus allen rationalen Zahlen kleiner als x. Insbesondere ist die reelle Zahl 1 die Menge aller rationalen Zahlen, die kleiner sind als 1. Jede positive Dezimaldarstellung bestimmt einen Dedekindschnitt: die Menge der rationalen Zahlen, die kleiner sind als eine bestimmte Stufe der Dezimalentwicklung. Also entspricht die reelle Zahl 0.999... der Menge der rationalen Zahlen r, sodass r < 0 oder r < 0.9 oder r < 0.99 oder r kleiner als eine Zahl der Form

${\begin{aligned}1-\left({\tfrac {1}{10}}\right)^{n}\end{aligned}}$.

Jedes Element von 0.999... ist kleiner 1, also auch ein Element der Zahl 1. Umgekehrt ist ein Element der Zahl 1 eine rationale Zahl

${\begin{aligned}{\tfrac {a}{b}}<1\end{aligned}},$

woraus folgt

${\begin{aligned}{\tfrac {a}{b}}<1-\left({\tfrac {1}{10}}\right)^{b}\end{aligned}}.$

Da 0.999... und 1 die gleichen rationalen Zahlen enthalten, sind beide Mengen gleich: 0.999... = 1.

Die Definition der reellen Zahlen als Dedekindschnitte wurde 1872 von Richard Dedekind vorgestellt. Der obige Ansatz, jeder Dezimalentwicklung eine reelle Zahl zuzuweisen, ist eine didaktische Veröffentlichung von Fred Richman im Mathematics Magazine. Er legt dar, dass Dedekindschnitte in jeder dichten Teilmenge der rationalen Zahlen zu dem gleichen Ergebnis führen. Außerdem erklärt er, warum die Definition eines Schnittes durch {x : x < 1} und nicht {x : x ≤ 1 } geben wird. Und zwar, um Existenz verschiedener Zahlen 0.999... und 1 apriori auszuschließen. Die Gleichheit ist also schon zu Beginn eingebaut. Unter anderen Umständen muss die Gleichheit nicht gegeben sein (siehe #Alternative Zahlensysteme unten).

Cauchyfolgen

→ Hauptartikel: Cauchyfolge

Die reellen Zahlen können ebenfalls als Grenzwert einer Cauchyfolge von rationalen Zahlen definiert werden. Der Abstand zwischen x und y ist definiert als ihr Betrag |x - y|. Die reellen Zahlen werden über diejenigen Folgen definiert, die die Cauchyeigenschaft mit diesem Abstand aufweisen. Die besagt, dass in einer Folge (x₀, x₁, x₂, ...) zu jeder positiven rationalen Zahl δ ein N aus den natürlichen Zahlen existiert, sodass |x_m − x_n| ≤ δ für alle m, n > N. (Der Abstand zwischen zwei Folgengliedern unterschreitet jede beliebige rationale Zahl.)

Wenn (x_n) und (y_n) zwei Cauchyfolgen sind, dann heißen sie als reelle Zahlen gleich, wenn die Folge ihrer Abstände (x_n − y_n) den Grenzwert 0 hat. Verschieden weite Dezimalentwicklungen einer Zahl b₀.b₁b₂b₃... ergeben eine Cauchyfolge. Diese kann genommen werden, um den reellen Wert der Zahl zu definieren. Daher besteht nun die Aufgabe darin, zu zeigen, dass die Folge der rationalen Zahlen

$\left(1-0,1-{9 \over 10},1-{99 \over 100},\dots \right)=\left(1,{1 \over 10},{1 \over 100},\dots \right)$

den Grenzwert 0 hat. Betrachtet man das nte Glied der Folge, muss also gezeigt werden, dass

$\lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.$

Dieser Grenzwert ist klar; Ein möglicher Beweis ist, in der Definition des Grenzwertes für ε = a/b > 0 N = b zu wählen. Wieder ergibt sich 0.999... = 1.

Die Definition der reellen Zahlen als Cauchyfolgen wurde erstmals von Eduard Heine und Georg Cantor, ebenfalls im Jahr 1872, vorgeschlagen. Der obige Ansatz über Dezimalentwicklungen sowie der konkrete Beweis folgen Griffiths' und Hiltons A comprehensive textbook of classical mathematics: A contemporary interpretation. Das Buch betrachtet vertraute Konzepte mit zeitgemäßen Methoden.

Unendliche Dezimalrepräsentationen

Auf dem Niveau des Mittelstufenunterrichts werden reelle Zahlen meist durch folgende Konstruktion eingeführt. Eine reelle Zahl wird definiert durch eine Ganzzahl, gefolgt von einem Komma und einer unendlich langen Kette von Dezimalziffern, die den Nachkommaanteil angeben. In dieser Konstruktion entspricht die Menge aller Kombinationen aus ganzer Zahl und Ziffern nach dem Komma der Menge der reellen Zahlen. Es kann streng gezeigt werden, dass dies den Axiomen der reellen Zahlen genügt, falls auch eine Äquivalenzrelation mit 0.999... = 1 definiert wird. Dies muss auch für alle anderen Dezimalrepräsentationen ungleich Null gewährleistet werden, deren Nachkommastellen nur endlich viele Ziffern ungleich null enthalten, und dem entsprechenden Gegenstück mit abschließenden 9en. Beweise der Gleichheit von 0.999... und 1, die auf dieser Konstruktion beruhen, ergeben sich also schon implizit.

Verallgemeinerungen

Das Ergebnis, dass 0.999... = 1 kann ohne Weiteres auf zwei Arten verallgemeinert werden. Zum einen hat jede Zahl, die durch eine endliche Dezimalentwicklung (entspricht unendlich vielen abschließenden 0en) repräsentiert wird, ein Gegenstück mit abschließenden 9en. Z. B. 0.25 und 0.24999... Diese Zahlen sind genau die Dezimalbrüche und sie sind dicht.

Zum anderen gilt die Entsprechung bei jeder anderen Basis ebenfalls. Zum Beispiel gilt zur Basis 2 (Dualsystem) die Gleichheit 0.111... = 1 und zur Basis 3 (Ternärsystem) ist 0.222... = 1. Lehrbücher der Analysis lassen das Beispiel der 0.999... meist aus und beginnen direkt bei der Verallgemeinerung.

Alternative Repräsentationen der 1 existieren auch für nicht-ganzzahlige Basen. Mit dem goldenen Schnitt als Basis sind dies 1.000... und 0.101010.... Es gibt unendlich viele weitere Repräsentationen der 1 zu dieser Basis. Allgemein gilt für fast alle q zwischen 1 und 2, dass es überabzählbar viele Entwicklungen der 1 zur Basis q gibt. Auf der anderen Seite gibt es auch überabzählbar viele Basen q (einschließlich der natürlichen Zahlen größer 1), zu denen es nur eine Dezimalentwicklung der 1 gibt, außer den trivialen 1.000... Dies entdeckten erstmals Paul Erdős, Miklos Horváth, und István Joó um 1990. Im Jahr 1998 bestimmten Vilmos Komornik und Paola Loreti die kleinste solche Basis, die nach ihnen benannte Komornik–Loreti Konstante q = 1.787231650... Zu dieser Basis gilt 1 = 0.11010011001011010010110011010011...; die Nachkommastellen werden durch die Thue-Morse-Folge, die sich nicht wiederholt, definiert.

Eine weiterreichende Verallgemeinerung betrifft die Nichtstandardzahlensysteme. In ihnen ergeben sich ebenfalls mehrere Repräsentationen und in gewissem Sinne gibt es hier noch größere Schwierigkeiten. Beispiele:

• Im balancierten Ternärsystem gilt: 1/2 = 0.111... = 1.111...
• Im fakultätbasierten Zahlensystem gilt: 1 = 1.000... = 0.1234...

Unmöglichkeit einer eindeutigen Repräsentation

Dass all diese verschiedenen Zahlensysteme nicht im Stande sind, besimmte reelle Zahlen durch eindeutige Repräsentationen darzustellen, weist auf einen fundamentalen Unterschied zwischen den reellen Zahlen als geordneter Menge und der lexikographisch geordneten Sammlung von unendlich langen Zeichenketten (z. B. Dezimaldarstellungen) hin. Die folgenden zwei Eigenschaften sind der Grund dafür:

• Wenn ein Intervall von reellen Zahlen in zwei nichtleere Teile L und R zerlegt wird, sodass jedes Element von L kleiner ist als jedes aus R, dann enthält entweder L ein größtes Element oder R ein kleinstes, aber nicht beides.
• Die Sammlung unendlich langer Zeichenketten bestehend aus Symbolen eines endlichen Alphabets, lexikographisch geordnet, kann auf die gleiche Weise in zwei nichtleere Teile L und R zerlegt werden. Allerdings enthält dann L ein größtes und R ein kleinstes Element. Tatsächlich genügt es, zwei endliche Präfixe p₁ und p₂ von Elementen aus der Sammlung zu wählen, sodass sie sich nur in ihrem letzten Symbol unterscheiden und in diesem Symbol aufeinander folgende Werte haben. Nun definiert man als L die Menge aller Zeichenketten in der Sammlung, deren entsprechendes Präfix höchstens p₁ ist und als R den Rest, nämlich diejenigen, deren entsprechendes Präfix mindestens p₂. Dann hat L ein größtes Element, das mit p₁ beginnt und danach an jeder Stelle das größte Symbole des Alphabets trägt. Andersherum hat R ein kleinstes Element, das mit p₂ beginnt und dann an jeder weiteren Position das kleinste Symbol aufweist.

Der erste Punkt folgt aus grundlegenden Eigenschaften der reellen Zahlen: L ein Supremum und R hat ein Infimum; beide müssen gleich sein, denn eine reelle Zahl liegt entweder in R oder L, da beide disjunkt sind. Der zweite Punkt verallgemeinert das Paar 0.999.../1.000..., dass man durch p₁ = "0" und p₂ = "1" erhält. Tatsächlich muss man nicht das gleiche Alphabet für jede Position benutzen (beispielsweise können Zahlensysteme mit verschieden Basen genutzt werden). Es ist sogar möglich, die Menge aller möglichen Zeichenketten zu nehmen und dann nur zwei Einschränkungen zu fordern. Erstens darf an jeder Position nur ein endliches Alphabet zur Verfügung stehen, damit gewährleistet ist, dass Minimum und Maximum gefunden werden können. Zweitens muss aus einer gültigen Wahl der einzelnen Zeichen eine Gültigkeit der gesamten Zeichenkette folgen. Unter diesen Bedingungen ergibt sich das Argument von oben, da eine ordnungserhaltende Abbildung zwischen der Menge dieser Zeichenketten und einem Intervall reeller Zahlen keine Bijektion sein kann: Entweder gibt es Zahlen, die durch keine Zeichenkette repräsentiert werden oder manche Zahlen werden doppelt repräsentiert.

Marko Petkovšek bewies, dass für alle Zahlensysteme, die alle reellen Zahlen darstellen, die Teilmenge der reellen Zahlen mit mehrfacher Repräsentation dicht ist.

Anwendungen

Eine Anwendung von 0.999... als einer Repräsentation von 1 findet sich in der elementaren Zahlentheorie. H. Goodwin veröffentlichte 1802 die Entdeckung von 9en in der periodischen Dezimalentwicklungen von Brüchen, deren Nenner bestimmte Primzahlen sind. Zum Beispiel:

• 1/7 = 0.142857142857... und 142 + 857 = 999.
• 1/73 = 0.0136986301369863... und 0136 + 9863 = 9999.

E. Midy bewies 1836 eine Allgemeine Aussage über solche Brüche, den Satz von Midy. Ein moderner Beweis dieses Satzes von W. G. Leavitt nutzt die Gleichheit 0.999... = 1 direkt. Wenn eine Dezimalzahl der Form 0.b₁b₂b₃... eine positive ganze Zahl ist, dann muss es 0.999... sein. Das ist der Ursprung der 9en in dem Satz. Überlegungen in diese Richtung führen auf Konzepte wie größte gemeinsame Teiler, Kongruenz in der Zahlentheorie, Fermat-Zahlen, die Ordnung eines Gruppenelementes und das quadratische Reziprozitätsgesetz.

In der Analysis spielt das Pendant zur Basis 3, 0.222... = 1, eine Schlüsselrolle zur Charakterisierung des Fraktals der Cantormenge.

• Ein Punkt im Einheitsintervall liegt genau dann in der Cantormenge, wenn er ternär mit ausschließlich den Ziffern 0 und 2 dargestellt werden kann.

Die n-te Stelle der Repräsentation gibt die Position des Punktes im n-ten Konstruktionsschritt an. Z. b. wird dem Punkt 2/3 die Repräsentation 0.2=0.2000... gegeben, da er zur Rechten ("2") der ersten Auslöschung und zur Linken ("1") jeder weiteren liegt. Der Punkt 1/3 wird nicht mit 0.1 angegeben, sondern mit 0.0222..., da er links von der ersten Auslöschung und rechts von jeder weiteren liegt.

Die sich wiederholenden 9en tauchen auch in einer weiteren Arbeit Cantors auf. Das Prinzip muss genutzt werden, um sein Diagonalargument auf Dezimalentwicklungen anzuwenden und einen Beweis für die Überabzählbarkeit des Einheitsintervalls zu liefern. Ein solcher Beweis muss nämlich reelle Zahlen aufgrund ihrer Dezimalentwicklung unterscheiden und deshalb Paare wie 0.2 und 0.1999... vermeiden.

Skepsis im Unterricht

Schüler und auch Studenten lehnen die Gleichheit 0.999... = 1 oft ab, aus Gründen, die von der verschiedenen Erscheinung zu Zweifeln am Konzept des Grenzwert reichen. Verschiedene Faktoren tragen zur Verwirrung bei:

• Schüler werden oft an die Vorstellung gewöhnt, eine Zahl werde durch eine einzige Dezimaldarstellung repräsentiert. Zwei offenkundig verschiedene Darstellungen, die die gleiche Zahle repräsentieren, erscheint paradox, was durch das vermeindliche gute Verstädnis der Zahl 1 verstärkt wird.
• Gelegenlich wird eine Zeichenkette wie "0.999..." als beliebig lange, aber endliche Kette angesehen. Ihre Länge mag zwar nicht festgelegt sein, jedoch wird am Ende stets eine letzte 9 erwartet.
• Intuition und unpräziser Unterricht führen zu der Vorstellung, dass der Grenzwert einer Folge ein unendlicher Prozess und nicht ein fester Wert ist.