Papierformat

	DIN EN ISO 216
Bereich	Bürowesen
Titel	Schreibpapier und bestimmte Gruppen von Drucksachen – Endformate – A- und B-Reihen und Kennzeichnung der Maschinenlaufrichtung
Kurzbeschreibung:	ISO-Papierformate
Letzte Ausgabe	2007-12
ISO	216

	DIN 476-2
Bereich	Papier und Papierprodukte für Datenverarbeitung, Büro und Schule
Titel	Papier-Endformate – C-Reihe
Kurzbeschreibung:	keine
Letzte Ausgabe	2008-02
ISO	keine, nationales Regelwerk

Papierformate A0 bis A8, Anschauungsmodell im Wissenschaftsmuseum von Barcelona: „Die Invasion der Quadratwurzeln“, Maßstab 1:1

Die Standardgrößen für Papierformate (siehe Papier) in Deutschland sind die vom Deutschen Institut für Normung (DIN) 1922 in der DIN-Norm DIN 476 festgelegten Formate. Entwickelt wurde der Standard vom Berliner Ingenieur Walter Porstmann. Der Entwurf gleicht den in Vergessenheit geratenen Entwürfen aus der Zeit der Französischen Revolution.

Die Deutsche Norm diente als Grundlage für das europäische bzw. internationale Äquivalent EN ISO 216, das wiederum in fast allen Ländern adaptiert worden ist. Unterschiede gibt es meist nur in den erlaubten Toleranzen. Nur DIN 476-2:2008-02 Papier-Endformate – C-Reihe ist heute noch gültig. Parallel existieren, etwa in den USA, Kanada und Mexiko, andere, weniger systematische Formatreihen.

In der Papier- und Druckindustrie lässt sich durch die Angabe der Dehnrichtung feststellen, ob es sich um ein Hoch- oder Querformat handelt. Dies wird durch einen Unterstrich (z.B.: 70 × 100) oder der Bezeichnung BB (Breitbahn) oder SB (Schmalbahn) gekennzeichnet. Die Dehnrichtung läuft immer quer zur Laufrichtung, da beim Stoffauflauf in der Papiermaschine die Fasern durch die Siebbewegung ausgerichtet werden und Zellstoff sich mehr in der Stärke als in der Länge bei Feuchtigkeitsaufnahme dehnt.

Internationale Papierformate (ISO/DIN)

Übersicht

Vergleich der DIN-Formate der Reihen A bis D
(ein Pixel entspricht einem Millimeter)

Es gibt 4 Reihen, die mit A bis D bezeichnet und jeweils in 11 Klassen unterteilt werden, welche nach absteigender Größe von 0 bis 10 durchnummeriert sind. Aus der Kombination dieser beiden Eigenschaften ergibt sich die übliche Bezeichnung, z. B. „A4“ (210 mm × 297 mm) oder „C6“ (114 mm × 162 mm), ggf. wird „DIN“ oder „ISO“ vorangestellt.

Davon abweichend gibt es in der DIN-, aber nicht in der ISO-Norm, Formate, die größer als die Klasse 0 sind. Diesen wird ein numerisches Präfix vorangestellt, z. B. „2A0“ für doppeltes A0.

Die Größe der Formate ist in ganzen Millimetern spezifiziert. Die Toleranz beträgt bei Maßen bis 150 mm ±1,5 mm, bei Maßen bis 600 mm ±2 mm und darüber ±3 mm.

Maße der ISO/DIN-Reihen A bis D (mm × mm)

Klasse	Reihe A	Reihe B	Reihe C	Reihe D	Benennung
4…0	1682 × 2378
2…0	1189 × 1682	1414 × 2000
…0	841 × 1189	1000 × 1414	917 × 1297	771 × 1091	Vierfachbogen
…1	594 × 841	707 × 1000	648 × 917	545 × 771	Doppelbogen
…2	420 × 594	500 × 707	458 × 648	385 × 545	Bogen
…3	297 × 420	353 × 500	324 × 458	272 × 385	Halbbogen
…4	210 × 297	250 × 353	229 × 324	192 × 272	Viertelbogen (z.B. A4)
…5	148 × 210	176 × 250	162 × 229	136 × 192	Blatt bzw. Achtelbogen
…6	105 × 148	125 × 176	114 × 162	96 × 136	Halbblatt (z.B. C6)
…7	74 × 105	88 × 125	81 × 114	68 × 96	Viertelblatt
…8	52 × 74	62 × 88	57 × 81		Achtelblatt
…9	37 × 52	44 × 62	40 × 57
…10	26 × 37	31 × 44	28 × 40

Die nominelle Fläche eines A0-Bogens entspricht einem (1) Quadratmeter, doch durch die Rundung der Seitenlängen auf ganze Millimeter ergeben sich nicht exakt die zu erwartenden Flächen von Bruchteilen eines Quadratmeters in der A-Reihe und entsprechender Vielfacher von √2 in den anderen Reihen. Wegen der zugelassenen Toleranzen können gemessene Längen und Flächen noch weiter abweichen.

Nominelle Flächen der ISO/DIN-Reihen A bis D (m2) Klasse Reihe A Reihe B Reihe C Reihe D 4…0 4 = 22 2…0 2 = 21 2√2 = 21½ …0 1 = 20 √2 = 2½ √√2 = 2¼ 1⁄√√2 = 2−¼ …1 1⁄2 = 2−1 √2⁄2 = 2−½ √√2⁄2 = 2−¾ 1⁄2√√2 = 2−1¼ …2 1⁄4 = 2−2 √2⁄4 = 2−1½ √√2⁄4 = 2−1¾ 1⁄4√√2 = 2−2¼ …3 1⁄8 = 2−3 √2⁄8 = 2−2½ √√2⁄8 = 2−2¾ 1⁄8√√2 = 2−3¼ …4 1⁄16 = 2−4 √2⁄16 = 2−3½ √√2⁄16 = 2−3¾ 1⁄16√√2 = 2−4¼ …5 1⁄32 = 2−5 √2⁄32 = 2−4½ √√2⁄32 = 2−4¾ 1⁄32√√2 = 2−5¼ …6 1⁄64 = 2−6 √2⁄64 = 2−5½ √√2⁄64 = 2−5¾ 1⁄64√√2 = 2−6¼ …7 1⁄128 = 2−7 √2⁄128 = 2−6½ √√2⁄128 = 2−6¾ 1⁄128√√2 = 2−7¼ …8 1⁄256 = 2−8 √2⁄256 = 2−7½ √√2⁄256 = 2−7¾ …9 1⁄512 = 2−9 √2⁄512 = 2−8½ √√2⁄512 = 2−8¾ …10 1⁄1024 = 2−10 √2⁄1024 = 2−9½ √√2⁄1024 = 2−9¾

Reale Flächen der ISO/DIN-Reihen A bis D (mm2) Klasse Reihe A Reihe B Reihe C Reihe D 4…0 3.999.796 2…0 1.999.898 2.828.000 …0 999.949 1.414.000 1.189.349 841.161 …1 499.554 707.000 594.216 420.195 …2 249.480 353.500 296.784 209.825 …3 124.740 176.500 148.392 104.720 …4 62.370 88.250 74.196 52.224 …5 31.080 44.000 37.098 26.112 …6 15.540 22.000 18.468 13.056 …7 7.770 11.000 9.234 6.528 …8 3.848 5.456 4.617 …9 1.924 2.728 2.280 …10 962 1.364 1.120

Herleitung

Aufteilung eines A0-Bogens. Die Formate ergeben sich jeweils durch Halbierung des nächstgrößeren.

Alle Formate lassen sich durch die folgenden Bedingungen herleiten:

1. Alle Formate innerhalb einer Reihe sind einander geometrisch ähnlich.
2. Die Halbierung des Formats Xn an der langen Seite ergibt das Format X(n + 1).
3. Das Format A0 hat einen Flächeninhalt F_A0 von 1 m².

Die B-, C- und D-Reihe werden aus der A-Reihe abgeleitet. (siehe unten)

Sind mit $h_{Xn}\,$ Höhe, $b_{Xn}\,$ Breite, $c_{Xn}\,$ Seitenverhältnis und $d_{Xn}\,$ Diagonale des Formats Xn bezeichnet so gilt:

$c_{Xn}=\frac{h_{Xn}}{b_{Xn}}\,$ die Bedingung der Ähnlichkeit (1)sagt aus, dass

$\frac{h_{Xn+1}}{b_{Xn+1}}=c_{Xn+1}=c_{Xn}=\frac{h_{Xn}}{b_{Xn}}.$

Die Halbierungsbedingung (2) ergibt

$h_{Xn+1}\,=b_{Xn}\,$

und $b_{Xn+1}=\tfrac{1}{2}h_{Xn}.$

Zusammen folgt daraus, dass

$\frac{b_{Xn}}{\tfrac{1}{2}h_{Xn}}=c_{Xn}=\frac{h_{Xn}}{b_{Xn}},$

und deshalb

$c_{Xn}^2=2.$

Das Seitenverhältnis beträgt also in jedem Format $\sqrt{2}:1$ (etwa $1{,}414:1\,$).

Damit folgt für die Fläche, Höhe, Breite und Diagonale aller Reihen:

$\begin{align}F_{Xn} &= h_{Xn} \cdot b_{Xn} &&= d_{Xn}^2 \cdot \tfrac{\sqrt2}{3} \\ &= \sqrt2\cdot b_{Xn}^2 &&= \tfrac{1}{\sqrt2}\cdot h_{Xn}^2 \\ h_{Xn} &= \sqrt2\cdot b_{Xn} & b_{Xn} &= \tfrac{1}{\sqrt2} \cdot h_{Xn}\\ &= \sqrt[4]2 \cdot \sqrt{F_{Xn}} &&= \tfrac{1}{\sqrt[4]2} \cdot \sqrt{F_{Xn}}\\ d_{Xn} &= \sqrt{h_{Xn}^2 + b_{Xn}^2} &&= \sqrt{\tfrac{3}{\sqrt2} \cdot F_{Xn}}\\ &= \sqrt3 \cdot b_{Xn} &&= \sqrt{1\tfrac12} \cdot h_{Xn} \end{align}$

Die Abmessungen ergeben sich auch rekursiv:

$\begin{align} h_{Xn} &= h_{Xm} \cdot \tfrac{1}{\sqrt2} & b_{Xn} &= b_{Xm} \cdot \tfrac{1}{\sqrt2}, && m=n-1\\ F_{Xn} &= \left(\tfrac{1}{\sqrt2}\cdot h_{Xm}\right) \cdot \left(\tfrac{1}{\sqrt2}\cdot b_{Xm}\right)\\ &= \tfrac12 \cdot h_{Xm} \cdot b_{Xm}\\ &= \tfrac12 \cdot F_{Xm}\end{align}$

A-Reihe

Maße der ISO/DIN-Reihen A

Größe	b (mm)	h (mm)	F (dm²)
4A0	1682	2378	400
2A0	1189	1682	200
A0	841	1189	100
A1	594	841	50,0
A2	420	594	24,9
A3	297	420	12,5
A4	210	297	6,24
A5	148	210	3,11
A6	105	148	1,55
A7	74	105	0,777
A8	52	74	0,385
A9	37	52	0,192
A10	26	37	0,096

Für die A-Reihe ergibt sich daraus:

$\begin{align} F_{\mathrm{A}n} &= 2^{-n}\text{ m}^2\\ h_{\mathrm{A}n} &= 2^{\frac14}\cdot \sqrt{2^{-n}}\,\text{m} & b_{\mathrm{A}n} &= 2^{-\frac14}\cdot \sqrt{2^{-n}}\,\text{m} \\ &= \sqrt{2^{\frac12 - n}}\,\text{m} &&= \sqrt{2^{-\frac12 - n}}\,\text{m}\\ &= \sqrt[4]{2^{1 - 2n}}\,\text{m} &&= \sqrt[4]{2^{-1 - 2n}}\,\text{m}\\ &= 2^{-\frac{n}2+\frac14}\,\text{m} &&= 2^{-\frac{n}2-\frac14}\,\text{m} \end{align}$

Die absoluten Abmessungen des A0-Formats ergeben sich zusammen mit der dritten Bedingung $h_{\mathrm{A}0}\cdot b_{\mathrm{A}0}=1 \text{ m}^2$ zu

$h_{\mathrm{A}0}=\sqrt[4]2\approx 1{,}189\text{ m}$ und $b_{\mathrm{A}0}=1:\sqrt[4]2\approx 0{,}841\text{ m}$.

Siehe auch: A4-Format

B-Reihe

Maße der ISO/DIN-Reihen B

Größe	b (mm)	h (mm)	F (dm²)
2B0	1414	2000	283
B0	1000	1414	141
B1	707	1000	70,7
B2	500	707	35,4
B3	353	500	17,7
B4	250	353	8,83
B5	176	250	4,40
B6	125	176	2,20
B7	88	125	1,10
B8	62	88	0,546
B9	44	62	0,273
B10	31	44	0,136

Die Höhen und Breiten und damit auch die Flächen F_Bn der Formate der B-Reihe errechnen sich aus dem geometrischen Mittel der Werte des entsprechenden (n) und des nächstgrößeren (m = n − 1) A-Formats:

$\begin{align}F_{\mathrm{B}n} &= \sqrt{F_{\mathrm{A}n} \cdot F_{\mathrm{A}m}} &&= \sqrt{2^{-n} \cdot 2^{-(n-1)}}\,\text{m}^2\\ &= \sqrt{h_{\mathrm{A}n} \cdot b_{\mathrm{A}n} \cdot h_{\mathrm{A}m} \cdot b_{\mathrm{A}m}} &&= \sqrt{2^{-2n+1}}\,\text{m}^2\\ &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{A}m}}\,\cdot\,\sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{A}m}} &&= 2^{\frac{-2n+1}2}\,\text{m}^2\\ &= h_{\mathrm{B}n} \cdot b_{\mathrm{B}n} &&= 2^{-n+\frac12}\,\text{m}^2\\ &= \tfrac12\cdot F_{\mathrm{B}m}\\ h_{\mathrm{B}n} &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{A}m}} & b_{\mathrm{B}n} &= \sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{A}m}} \\ &= 2^{-\frac{n}2+\frac12}\,\text{m} &&= 2^{-\frac{n}2}\,\text{m} \end{align}$

C-Reihe

Maße der ISO/DIN-Reihen C

Größe	b (mm)	h (mm)	F (dm²)
C0	917	1297	119
C1	648	917	59,4
C2	458	648	29,7
C3	324	458	14,8
C4	229	324	7,42
C5	162	229	3,71
C6	114	162	1,85
C7	81	114	0,923
C8	57	81	0,462
C9	40	57	0,228
C10	28	40	0,112

Die Abmessungen der C-Reihe ergeben sich wiederum aus dem geometrischen Mittel der A- und B-Formate gleicher Nummer (n):

$\begin{align}F_{\mathrm{C}n} &= \sqrt{F_{\mathrm{A}n} \cdot F_{\mathrm{B}n}} &&= \sqrt{2^{-n} \cdot 2^{-n+\frac12}}\,\text{m}^2\\ &= \sqrt{h_{\mathrm{A}n} \cdot b_{\mathrm{A}n} \cdot h_{\mathrm{B}n} \cdot b_{\mathrm{B}n}} &&= \sqrt{2^{-2n+\frac12}}\,\text{m}^2\\ &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{B}n}}\,\cdot\,\sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{B}n}} &&= 2^{\frac{-2n+\frac12}2}\,\text{m}^2\\ &= h_{\mathrm{C}n} \cdot b_{\mathrm{C}n} &&= 2^{-n+\frac14}\,\text{m}^2\\ &= \tfrac12\cdot F_{\mathrm{C}m}\\ h_{\mathrm{C}n} &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{B}n}} & b_{\mathrm{C}n} &= \sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{B}n}} \\ &= 2^{-\frac{n}2+\frac38} \,\text{m} &&= 2^{-\frac{n}2-\frac18}\,\text{m}\end{align}$

D-Reihe

Maße der ISO/DIN-Reihen D

Größe	b (mm)	h (mm)	F (dm²)
D0	771	1091	84,1
D1	545	771	42,0
D2	385	545	21,0
D3	272	385	10,5
D4	192	272	5,22
D5	136	192	2,61
D6	96	136	1,31
D7	68	96	0,653

Die Abmessungen der D-Reihe ergeben sich aus dem geometrischen Mittel der Werte des entsprechenden (n) A-Formates und des nächstkleineren (m = n + 1) B-Formats:

$\begin{align}F_{\mathrm{D}n} &= \sqrt{F_{\mathrm{A}n} \cdot F_{\mathrm{B}m}} &&= \sqrt{2^{-n} \cdot 2^{-(n+1)+\frac12}}\,\text{m}^2 \\ &= \sqrt{h_{\mathrm{A}n} \cdot b_{\mathrm{A}n} \cdot h_{\mathrm{B}m} \cdot b_{\mathrm{B}m}} &&= \sqrt{2^{-2n-\frac12}}\,\text{m}^2 \\ &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{B}m}}\,\cdot\,\sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{B}m}} &&= 2^{\frac{-2n-\frac12}2}\,\text{m}^2 \\ &= h_{\mathrm{D}n} \cdot b_{\mathrm{D}n} &&= 2^{-n-\frac14}\,\text{m}^2\\ &= \tfrac12\cdot F_{\mathrm{D}m}\\ h_{\mathrm{D}n} &= \sqrt{h_{\mathrm{A}n} \cdot h_{\mathrm{B}m}} & b_{\mathrm{D}n} &= \sqrt{b_{\mathrm{A}n} \cdot b_{\mathrm{B}m}} \\ &= 2^{-\frac{n}2-\frac38}\,\text{m} &&= 2^{-\frac{n}2+\frac18}\,\text{m}\end{align}$

Größenverhältnis

Der Größe nach geordnet ergibt sich die Folge

$\begin{align} \ldots &> F_{\mathrm{D}(n-1)} &&> F_{\mathrm{B}n} &&> F_{\mathrm{C}n} &&> F_{\mathrm{A}n} &&> F_{\mathrm{D}n} &&> F_{\mathrm{B}(n+1)} &> \ldots\\ \ldots &> 2^{-n+\frac34} &&> 2^{-n+\frac12} &&> 2^{-n+\frac14} &&> 2^{-n} &&> 2^{-n-\frac14} &&> 2^{-n-\frac12} &> \ldots \end{align}$

Je zwei aufeinanderfolgende Formate in dieser Folge stehen im Längenverhältnis $1:\sqrt[8]2.$

Anwendungen

Für einen Inhalt im A-Format wird typischerweise ein Briefumschlag des entsprechenden C-Formats gewählt, der wiederum in einem Umschlag der B-Reihe Platz findet. Die Höchstmaße von Briefsendungen im Postverkehr orientieren sich an der B-Reihe.

A0, A1	Technische Zeichnungen, See-/Landkarten, Druckbogen, Aushang-Fahrpläne, Poster, Filmplakate, Wahlplakate
A1, A2	Flipcharts, Geschenkpapier, Filmplakate, Fahrpläne, Kalender, Zeitungen, Meisterbrief, Technische Zeichnungen
A2, A3	Zeichnungen, Diagramme, große Tabellen, Kalender, Karten, Filmplakate, Technische Zeichnungen
B4, A3	Zeitungen, Noten, Karten
A4	Briefpapier, Formulare, Hefte, Zeitschriften, Technische Zeichnungen
A5	Notizblöcke, Schulhefte, Prospekte
D5	DVD-Hüllen
A5, A6, A7, A8	Karteikarten, selten auch A4 und A9
A6	Flyer, Postkarten, Taschenbücher, Überweisungsträger, Notizhefte
B5, A5, B6, A6, A4	Bücher (Buchformat)
A7	Flugblätter, Taschenkalender, Personalausweis (ID-2)
B7	Reisepass (ID-3)
B8, A8	Spielkarten, Visitenkarten, Etiketten
C4, C5, C6, B4	Umschläge

Abgeleitete Formate

Streifenformate, Umschläge

Streifenformate, die aus der A-Reihe durch Teilung abgeleitet werden

Bezeichnung	Abmessungen (mm × mm)	Seitenverhältnis	Bemerkung
1⁄4 A3	105 × 297	2√2:1
1⁄3 A4	99 × 210	3⁄2√2:1
1⁄4 A4	74 × 210	2√2:1
1⁄8 A4	37 × 210	4√2:1
1⁄3 A5	70 × 148	3⁄2√2:1
1⁄6 DIN (Norm)	198 × 210	3⁄4√2:1	eigentlich „2⁄3 A4“
1⁄6 DIN (Praxis)	200 × 210	1,05:1

Weitere Formate für Briefumschläge

Bezeichnung	Abmessungen (mm × mm)	Seitenverhältnis	Bemerkung
DL (DIN lang)	110 × 220	2:1	vgl. 1⁄3 A4
C6/C5	114 × 229	2:1	kurze Seite von C6 mit langer Seite von C5, etwas größer als DL, fasst größere Blattanzahl

JIS B-Serie

Die japanische Norm JIS P 0138-61 übernimmt die A- und C-Serien von ISO bzw. DIN, definiert aber eine leicht andere B-Serie: JIS B0 hat eine Fläche von 1,5 m², dem arithmetischen und nicht geometrischen Mittel der Flächen von A0 und 2A0, Breiten und Höhen werden analog zu A ermittelt und entsprechend gerundet.

Der Ursprung der japanischen B-Serie liegt darin, dass dieses Format kompatibel zum bereits verwendeten Shiroku-ban mit seinen Abmessungen von 127 mm × 188 mm sein sollte, welches wiederum seine Herkunft im amtlich verwendeten Format Mino-ban der Edo-Zeit hatte. Das Shiroku-ban wurde so fast identisch mit dem neuen JIS B6.

Gegenüberstellung der DIN-/ISO- und der JIS-B-Reihe (in Millimetern)

Format	Maße (mm × mm)		Fläche (mm²)
	DIN/ISO	JIS	DIN/ISO	JIS
B0	1000 × 1414	1030 × 1456	1.414.000	1.499.680
B1	0707 × 1000	0728 × 1030	707.000	749.840
B2	0500 × 0707	0515 × 0728	353.500	374.920
B3	0353 × 0500	0364 × 0515	176.500	187.460
B4	0250 × 0353	0257 × 0364	88.250	93.548
B5	0176 × 0250	0182 × 0257	44.000	46.774
B6	0125 × 0176	0128 × 0182	22.000	23.296
B7	0088 × 0125	0091 × 0128	11.000	11.648
B8	0062 × 0088	0064 × 0091	5.456	5.824
B9	0044 × 0062	0045 × 0064	2.728	2.880
B10	0031 × 0044	0032 × 0045	1.364	1.440

Überformate

Da beim Beschneiden und Falzen Verluste auftreten, wurden die Überformate RA und SRA geschaffen. Das R steht für „Rohformat“, S für „sekundäres“. RA0 hat prinzipiell eine Fläche von 1,05 m², SRA0 1,15 m², Breite und Höhe sind aber auf halbe Zentimeter gerundet.

ISO/DIN-Reihen RA und SRA (in Millimetern)

Klasse	RA	SRA
0	860 × 1220	900 × 1280
1	610 × 860	640 × 900
2	430 × 610	450 × 640
3	305 × 430	320 × 450
4	215 × 305	225 × 320

Unter der inoffiziellen Bezeichnung A4+ (A4 plus) existiert ferner ein auf dem DIN-A4-Format basierendes Überformat, das beim Einsatz in Tintenstrahl- und Laserdruckern Verwendung findet. Es wird für Endkunden speziell von Druckerherstellern angeboten. Durch die fehlende Normierung dieses Überformates existieren verschiedene Formate. So existieren auf DIN A4 basierende Formate mit einer einheitlichen Beschnittzugabe von jeweils drei Millimetern pro Seite (216 mm × 303 mm) oder randlos bedruckbare Formate mit Abrisskanten. Einige (amerikanische) Anbieter spezifizieren das Format A4+ auch mit dem Maß 9½ in × 13 in (241 mm × 330 mm). Im Foto- und Werbedruck existiert auch das nicht normierte Überformat A3+ (A3 plus), auch unter Super A3 oder Super B bekannt, auch hier gibt es kein festgelegtes einheitliches Maß. Die Abmessungen sind meist so gewählt, dass auf einem Drucker des Papierherstellers eine A3-Seite randlos ausgedruckt werden kann.

Anmerkungen

• Entgegen einer verbreiteten Annahme entspricht das Seitenverhältnis der vier DIN-Reihen (1 : 1,414) nicht dem Goldenen Schnitt $\textstyle\frac{1+\sqrt5}2$. Andere Formate, bspw. Oktav, verwenden hingegen dieses Verhältnis von etwa 1 : 1,618.
• Dass die (1 : √2)-Form nicht nur für die vorliegende Aufgabe die richtige sei, sondern auch „etwas angenehmes und vorzügliches vor der gewöhnlichen“ habe, ist eine bereits 1786 vom Physiker und Aphorismen-Dichter Georg Christoph Lichtenberg gemachte Feststellung.
• Die DIN 476 wurde bereits in der Zeit der Französischen Revolution vorweggenommen. Es existierten Papierformate in exakt den Abmessungen dieser Norm. DIN hat die vergessenen französischen Vorarbeiten lediglich neu entdeckt und durchgesetzt.
• Das Papiergewicht wird üblicherweise als Quadratmetergewicht angegeben. Durch die einfachen Seitenverhältnisse berechnet sich die Masse eines üblichen A4-Bogens mit 80 g/m² zu exakt

  $80\,\frac{\text{g}}{\text{m}^2} \cdot \frac{1}{2^4}\,\text{m}^2 = 80\,\frac{\text{g}}{\text{m}^2} \cdot \frac{1}{16}\,\text{m}^2 = 5\,\text{g}$.

• Das Papiervolumen: Unter Volumen versteht man bei Papier seine Dicke. Papier kann bei gleichem Gewicht unterschiedlich dick hergestellt werden. Papier mit größerem Volumen ist „griffiger“. Von „normalem Volumen“ 1 ausgehend, werden die Volumen in ¼-Stufen größer. 90-g-Papier mit dem Volumen 2 ist doppelt so dick wie 90-g-Papier mit dem Volumen 1.
• Beim Vergrößern und Verkleinern mit einem Fotokopierer ist die Längen- und nicht die Flächenänderung anzugeben: das nächstgrößere bzw. nächstkleinere Format ergibt sich durch Skalierungsfaktor 141 % (√2) bzw. 71 % (√½), während 200 % und 50 % jeweils ein Format überspringen.

Formate für spezielle Anwendungen

Außerdem gab und gibt es natürlich andere Systeme, beispielsweise bei Zeitungen. Manche alte Systeme haben sich zumindest in Teilen bis heute erhalten.

Maschinenformate

Für die Verarbeitung in Druckmaschinen gibt es einen Industriestandard, der folgende maximalen Papiergrößen umfasst.

Maschinenformate (mm × mm)

Formatklasse	Abmessungen	Bezeichnung
00	350 × 500	Kleinformat
01	460 × 640
0b	520 × 720	Halbformat
1	560 × 830
2c	640 × 910
2	610 × 860
3	650 × 960
3b	720 × 1020	Mittelformat
4	780 × 1120
5	890 × 1260
6	1020 × 1420
7	1120 × 1620
7b	1200 × 1620	Großformat
8	1300 × 1850
9	1500 × 2050	Supergroßformat
10	1620 × 2240

Verpackungsbogen

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (bspw. Einzelnachweisen) ausgestattet. Die fraglichen Angaben werden daher möglicherweise demnächst entfernt. Hilf bitte der Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Näheres ist eventuell auf der Diskussionsseite oder in der Versionsgeschichte angegeben. Bitte entferne zuletzt diese Warnmarkierung. Industrielle Gepflogenheit nachlesbar zitieren.

Im Verpackungsbereich kommen Formate zum Einsatz, die sich vom Ballenformat (75 cm × 100 cm) ableiten. Diese Formate beschränken sich nicht auf Papierbögen, sondern werden auch bei anderen Zuschnitten, z.B. aus Folie, verwendet. Ein Folgeformat entsteht jeweils durch Halbierung der langen Seite.

Verpackungsbogen

Kennung	Gebräuchlicher Name	Abmessungen (mm × mm)	Verwendungsbeispiele
1/1	Ganzer Bogen	750 × 1000	Verpackungspapiere, Stopfpapier
1/2	Halber Bogen	500 × 750	Brotseidenpapier, Bäckereipapiere
1/4	Viertelbogen	375 × 500	Frischhaltepapier in Metzgereien, Käsereien
1/8	Achtelbogen	250 × 375
1/16	Sechzehntelbogen	180 × 250
1/32	Zweiunddreißigstelbogen	125 × 180	Zwischenlagen, z. B. bei Wurst, Käse, Konditoreiprodukten
1/64	Vierundsechzigstelbogen	90 × 125

Zeitplansysteme

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (bspw. Einzelnachweisen) ausgestattet. Die fraglichen Angaben werden daher möglicherweise demnächst entfernt. Hilf bitte der Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Näheres ist eventuell auf der Diskussionsseite oder in der Versionsgeschichte angegeben. Bitte entferne zuletzt diese Warnmarkierung. Übliches nachlesbar zitieren.

Bei Zeitplansystemen (Kalender- und Zeitplan-Ringordner) sind weitere Formate üblich, die je nach Hersteller unterschiedliche Bezeichnungen und Lochungen besitzen. Zum Beispiel:

Zeitplansysteme

Name	Firma	Abmessungen
		mm × mm	in × in
WT	tempus.	86 × 145
Monarch	Franklin-Covey	216 × 279	8 1⁄2 × 11
Deskfax	Filofax	176 × 250
Classic	Franklin-Covey	140 × 216	5 1⁄2 × 8 1⁄2
Compact	Franklin-Covey	108 × 171	4 1⁄4 × 6 3⁄4
	Time/System	85 × 169
Pocket	Time/System	100 × 172
	Franklin-Covey	89 × 152	3 1⁄2 × 6
	Filofax	81 × 120
Midi	Chronoplan	96 × 172
Personal, Slimline	Filofax	95 × 171
Mini	Chronoplan	79 × 125
	Filofax	67 × 105
Partner	Time/System	75 × 130
M2	Filofax	64 × 103

Notendruck

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (bspw. Einzelnachweisen) ausgestattet. Die fraglichen Angaben werden daher möglicherweise demnächst entfernt. Hilf bitte der Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Näheres ist eventuell auf der Diskussionsseite oder in der Versionsgeschichte angegeben. Bitte entferne zuletzt diese Warnmarkierung. Auswahl nachlesbar zitieren.

Notendruckformate (in mm)

Formatklasse	Abmessungen
Großpartitur	420 × 680*
	300 × 420
	300 × 400
	285 × 400
	300 × 390
	290 × 350
Quartformat	270 × 340
Bachformat	240 × 325
N4	231 × 303
Oktavformat	170 × 270
Studienpartitur	170 × 240
Salonorchester	190 × 290
Klavierauszug	190 × 270
Klavierformat	235 × 310
Großmarsch	135 × 190
Marschformat	135 × 170

Formate in anderen Ländern

Nordamerika

Die ANSI-Reihe baut auf dem „Letter“-Format (ANSI A) auf. Durch Verdoppelung entsteht das jeweils nächstgrößere Format, alternierend in den Seitenverhältnissen 1 : 1,294 (ANSI A, C, E) und 1 : 1,545 (ANSI B, D).

Die in Nordamerika üblichen Papierformate folgen keinem einheitlichen Muster und sind ursprünglich zollbasiert (in). Die Reihe A bis E entstammt dem Standard ANSI/ASME Y14.1, andere Größen sind in ANSI X3.151-1987 festgelegt.

Die kanadischen Größen P1–P6 aus dem Standard CAN 2-9.60M sind in Millimetern spezifiziert und (bis auf P6) auf halbe Zentimeter gerundet. Näherungsweise entsprechen sie Zoll-Pendants. Sie lassen sich durch Verdopplung bzw. Halbierung ableiten. Ihre Bedeutung ist auch in Kanada selbst eher gering.

Sowohl die nordamerikanische ANSI-Reihe als auch die kanadischen Größen haben jedoch nicht die Vorteile des konstanten √2-Verhältnisses der DIN-Reihen, da sie abwechselnd Verhältnisse von ca. 1,30 und 1,55 aufweisen.

Gebräuchliche nordamerikanische Papierformate

Name	ANSI	in × in	mm × mm	CAN	mm × mm
				P6	107 × 140
Invoice		5½ × 8½	140 × 216	P5	140 × 215
Executive		7¼ × 10½	184 × 267
Legal		8½ × 14	216 × 356
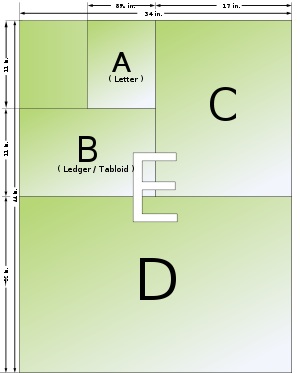
Letter	A	8½ × 11	216 × 279	P4	215 × 280
Ledger, Tabloid	B	11 × 17	279 × 432	P3	280 × 430
Broadsheet	C	17 × 22	432 × 559	P2	430 × 560
	D	22 × 34	559 × 864	P1	560 × 860
	E	34 × 44	864 × 1118
	F	28 × 40	711 × 1116

Eine besondere Bedeutung hat hier das Letter-Format mit 8½ × 11 Zoll (216 × 279 mm), da dieses durch den Schriftverkehr auch nach Europa gelangt. Das Blatt ist etwa 6 mm breiter und 18 mm kürzer und mit einer Fläche von 602,7 cm² etwas kleiner als das A4-Blatt mit 625 cm². Die gemeinsame Schnittfläche von Letter/A bzw. P4 und A4 beträgt im Rahmen der Toleranzgrenzen 21 cm × 28 cm und hat zufällig ein Seitenverhältnis von 3:4 (Diagonale 35 cm, Fläche 588 cm²); diese Größe wird mitunter als internationales Austausch- oder Kompromissformat verwendet.

Europäischen Nutzern begegnet das US-Letter-Format mitunter, wenn es in amerikanischer Software als Vorgabe für das Druckformat eingestellt ist oder durch derart gedruckte oder elektronische Dokumente (z.B. PDF).

Die Kartenfächer von Tankrucksäcken für Motorräder sind häufig für US-Letter ausgelegt.

Nordamerikanische Architektur- und Ingenieurspapierformate

Name	Ing.	Arch.	Ing.	Arch.
	in × in		mm × mm
A	8½ × 11	9 × 12	216 × 279	229 × 305
B	11 × 17	12 × 18	279 × 432	305 × 457
C	17 × 22	18 × 24	432 × 559	457 × 610
D	22 × 34	24 × 36	559 × 864	610 × 914
E	34 × 44	36 × 48	864 × 1118	914 × 1219
F	44 × 68		1118 × 1727

China

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (bspw. Einzelnachweisen) ausgestattet. Die fraglichen Angaben werden daher möglicherweise demnächst entfernt. Hilf bitte der Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Näheres ist eventuell auf der Diskussionsseite oder in der Versionsgeschichte angegeben. Bitte entferne zuletzt diese Warnmarkierung. Siehe Diskussion.

Chinesische Papierformate

Name	Format	Größe (mm × mm)
Kai (开 kāi)	8	260 × 370
	16	185 × 260
	32	130 × 185
	32 groß	140 × 203

Japan

In Japan werden neben der A-Reihe und der japanischen B-Reihe zusätzlich folgende Formate verwendet:

Name	mm × mm
Sango-ban (三五判)	084 × 148
Shinsho-ban (新書判)	103 × 182
Ko-B6-ban (小B6判)	112 × 174
Kiku-ban (菊判)	150 × 220
Shiroku-ban (四六判)	127 × 188
Jūbako-ban (重箱判)	182 × 206
AB-ban (AB判) Wide-ban (ワイド判, Waido-ban)	210 × 257

Die unbeschnittenen Papierbögen haben nach Norm JIS P 0202 folgende Größen:

Name	mm × mm
A-retsu homban (A列本判)	0625 × 0880
Kiku-ban (菊判)	0636 × 0939
B-retsu homban (B列本判)	0765 × 1085
Shiroku-ban (四六判)	0788 × 1091
Hatoron-ban (ハトロン判)	0900 × 1200
nicht in JIS P 0202
AB-ban (AB判)	0880 × 1085

Aus einem Bogen Kiku-ban werden 4×4 Blätter und aus einem Bogen Shiroku-ban 4×8 Blätter geschnitten. Sango-ban wird aus A-retsu homban; Jūbako-ban, Shinsho-ban, sowie Ko-B6-ban („Klein-B6“) aus B-retsu homban geschnitten.

In der Edo-Zeit benutzte die Regierung des Tokugawa-Shogunats ein Mino-ban (美濃判) genanntes Papierformat, welches eine Größe von 13 sun × 9 sun (394 mm × 273 mm) hatte. Mit der Modernisierung des Landes in der Meiji-Zeit wurden Bögen im unbeschnittenen britischen Crown-Format von 787 mm × 1092 mm verwendet, die dann auf 2×4 Blätter im Mino-ban zugeschnitten wurden. Da aus solchen Bögen 8 Blätter im Mino-ban entstanden, wurde diese Bögen Daiyatsu-ban (大八つ判, „Groß-8-Stück-Papierformat“) genannt. Später wurden diese Bögen in 32 Blätter je 103 mm × 182 mm geschnitten die ebenfalls zuerst Daiyatsu-ban hießen. In traditioneller Längenangabe entsprach dies ungefähr 4 (sprich shi) sun × 6 (sprich roku) sun, weswegen das Format bald Shiroku-ban genannt wurde. Für den Begriff Sango-ban gilt ähnliches da er seine ungefähre Größe 3 (san) sun × 5 (go) sun beträgt.

Das Kiku-ban geht auf amerikanische unbeschnittene Papierbögen dieser Größe zurück. Ein Handelsunternehmen soll diese unter dem Markennamen Dahlia (Dahlie) verkauft haben. Diese Blume wurde damals im Japanischen als Natsugiku (夏菊, wörtlich: „Sommer-Chrysantheme“) bezeichnet, was dann auf Kiku verkürzt (im Japanischen kann bei Wortverbindungen ein früherer Anfangskonsonant stimmhaft werden: k → g) worden sein soll. Eine andere Variante ist dass kiku eine Abkürzung für Zeitung (新聞, shimbun) ist, da das zweite Schriftzeichen auch als kiku gelesen werden kann.

AB-ban hat seinen Namen von der Verwendung der Breite von DIN A4 als Breite und der Breite von JIS B4 als Höhe.

Der Begriff Hatoron (ハトロン) bei Hatoron-ban ist eine Abkürzung von Deutsch „Patronenpapier“, auf Japanisch als パトローネンパピアー (Patorōnenpapiā) geschrieben, wobei man früher nicht immer die diakritischen Zeichen – hier den Kreis (handakuten) über ハ – schrieb.

Historische Formate

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (bspw. Einzelnachweisen) ausgestattet. Die fraglichen Angaben werden daher möglicherweise demnächst entfernt. Hilf bitte der Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Näheres ist eventuell auf der Diskussionsseite oder in der Versionsgeschichte angegeben. Bitte entferne zuletzt diese Warnmarkierung. Alle Historischen Formate nachlesbar zitieren: Zuordnung zwischen Name und Abmessungen.

Stellenweise, z.B. im Bibliothekswesen, sind noch heute Formate aus dem 19. Jahrhundert in Gebrauch. Einige Werte haben sich über die Zeit um teilweise mehr als ein Zoll verändert.

Historische europäische Formate

historische Papierformate (mm × mm)

Bezeichnung	Abmessungen
Oktav	142,5 × 225
Quart	225 × 285
Folio	210 × 330
Brief	270 × 420
Kanzlei, Doppelfolio	330 × 420
Propatria	340 × 430
Groß Patria	360 × 430
Bischof	380 × 480
Register, Löwen	400 × 500
Median I	420 × 530
Median	440 × 560
Post	460 × 560
Median II	460 × 590
Klein Royal	480 × 640
Royal	480 × 650
Lexikon	500 × 650
Super Royal	500 × 680
Imperial	570 × 780
Olifant	675 × 1082

Historische britisch-amerikanische Formate

Unsystematische historische nordamerikanische Papierformate

Name	in × in	mm × mm
Post	15½ × 19¼	394 × 489
Large Post	16½ × 21	419 × 533
Elephant	23 × 28	584 × 711
Medium	18 × 23	457 × 584
Crown	15 × 20	381 × 508
Double Crown	20 × 30	508 × 762
Royal	20 × 25	508 × 635
Quarto	8 × 10	203 × 254
Foolscap	8 × 13	203 × 330
Demy	17½ × 22½	445 × 572
Double Demy	22½ × 35	572 × 889
Quad Demy	35 × 45	889 × 1143
Dollar Bill	2 9/16 × 6	76 × 178

Sonstiges

Als Format für Radtourenbücher mit Spiralbindung zum Umblättern hat sich das Querformat mit 220 mm × 120 mm (+ halbe Spiralbreite) seit 1990 weitgehend durchgesetzt. Es passt in die Deckeltaschen vieler Lenkertaschen, die auch zu Rennlenkern passen, sowie hochkant in (große) Jackeninnentaschen. Gefaltete Wanderkarten weisen ähnlich große Hochformate mit Leporellofaltung auf. Genaue, große Straßenkarten und Stadtpläne sind für weniger windige Umgebung gedacht und daher häufig höher, also 11–12 cm × 25–27 cm. Pläne mit 10 cm × 16 cm und kleiner sind gut brust- und handtaschengängig.

Scheckkarten sowie viele andere Plastik- und Kartonkarten, wie Telefonwertkarten oder Visitenkarten, messen nach ISO 7810 als Format ID-1 86 mm × 54 mm.

Lochkarten mit 187 mm × 83 mm wurden in der elektronischen Datenverarbeitung bis etwa 1985 zur Datenein- und -ausgabe genutzt. Sie dienten mit Aufdruck gelegentlich auch als Rechnung oder Zahlschein.

Die Grammatur eines Papierbogens vom Format DIN A4 lässt sich genau bestimmen, indem man 16 Bögen wiegt, weil die Papiergröße A4 ein Sechzehntel von A 0 ist, das genau einen Quadratmeter groß ist.

Siehe auch

• Bildformat (Seitenverhältnis) – Papierformate für Kleinbildfotografie
• Buchformat
• Zeitungsformat
• Weltformat

Literatur

• Deutsches Institut für Normung e.V. (Hrsg.): DIN EN ISO 216:2007-12 – Schreibpapier und bestimmte Gruppen von Drucksachen – Endformate – A- und B-Reihen und Kennzeichnung der Maschinenlaufrichtung (ISO 216:2007); Deutsche Fassung EN ISO 216:2007. Beuth-Verlag, Berlin 2007

Weblinks

• Das Papierformat DIN A4
• Werner Brefeld: DIN-Papier und der Goldene Schnitt
• Markus Kuhn: International Standard Paper Sizes
• directTOOLS.de: Standard DIN – Papierformate
• IEEE-ISTO 5101.1-2002: The Printer Working Group Standard for Media Standardized Names (PDF)
• Umrechnen Papierformat
• Website über das DIN-A-Format