p-Norm

Die p-Normen sind in der Mathematik eine Klasse von Vektornormen, die für reelle Zahlen definiert sind. Wichtige Spezialfälle sind dabei die Summennorm , die euklidische Norm und als Grenzwert für die Maximumsnorm. Alle -Normen sind zueinander äquivalent, für wachsendes monoton fallend und erfüllen die Minkowski-Ungleichung sowie die Hölder-Ungleichung. Die Mengen konstanter -Norm (Einheitssphären) besitzen allgemein die Form von Superellipsoiden oder Subellipsoiden. Die -Normen bilden den Grundbaustein für Normen weiterer mathematischer Objekte, wie Folgen, Funktionen, Matrizen und Operatoren.
Definition[Bearbeiten | Quelltext bearbeiten]
Die -Norm eines reellen oder komplexen Vektors mit oder ist für reelles durch
definiert, wobei der Betrag der Komponente ist. Für die Definition ist es dabei unerheblich, ob es sich bei um einen Zeilen- oder einen Spaltenvektor handelt. Im Fall entsprechen alle -Normen der Betragsnorm einer reellen oder komplexen Zahl.
Die Menge der Vektoren mit -Norm eins wird Einheitssphäre der Norm genannt, wobei nur im Fall die Einheitssphäre tatsächlich der aus der Geometrie bekannten Sphäre entspricht. Die Einheitssphären der -Normen haben allgemein in zwei Dimensionen die Form von Superellipsen oder Subellipsen und in drei und höheren Dimensionen die Form von Superellipsoiden beziehungsweise Subellipsoiden.
Wichtige Spezialfälle[Bearbeiten | Quelltext bearbeiten]
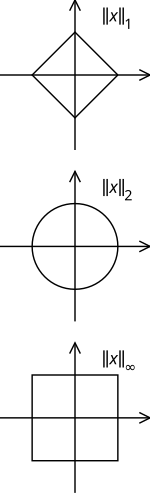
Summennorm[Bearbeiten | Quelltext bearbeiten]
Die 1-Norm wird auch Betragssummennorm oder kurz Summennorm genannt und ist durch
definiert. Sie entspricht der Summe der Beträge der Komponenten des Vektors. Die Einheitssphäre der reellen Summennorm hat in zwei Dimensionen die Form eines Quadrats, in drei Dimensionen die Form eines Oktaeders und in allgemeinen Dimensionen die Form eines Kreuzpolytops.
Euklidische Norm[Bearbeiten | Quelltext bearbeiten]
Die 2-Norm ist die euklidische Norm und durch
definiert. Sie entspricht der Wurzel aus der Summe der Betragsquadrate der Komponenten des Vektors. Die Einheitssphäre der reellen euklidischen Norm hat in zwei Dimensionen die Form eines Kreises, in drei Dimensionen die Form einer Kugeloberfläche und in allgemeinen Dimensionen die Form einer Sphäre. In zwei und drei Dimensionen beschreibt die euklidische Norm die anschauliche Länge eines Vektors in der Ebene oder im Raum.
Maximumsnorm[Bearbeiten | Quelltext bearbeiten]
Für den Grenzwert erhält man die ∞-Norm (Unendlich-Norm), die oft auch zu den -Normen gezählt wird. Sie wird auch Maximumsnorm oder Tschebyschow-Norm genannt und ist durch
definiert. Sie entspricht damit dem Betrag der betragsgrößten Komponente des Vektors. Die Einheitssphäre der reellen Maximumsnorm hat in zwei Dimensionen die Form eines Quadrats, in drei Dimensionen die Form eines Würfels und in allgemeinen Dimensionen die Form eines Hyperwürfels.
Dass die Maximumsnorm tatsächlich als Grenzwert der -Normen für entsteht, folgt für aus
- ,
da für die Summe gilt und somit der Grenzwert von für gleich Eins ist. Die untere Schranke von wird dabei für einen Vektor angenommen, dessen Komponenten bis auf eine alle gleich Null sind, und die obere Schranke für einen Vektor, dessen Komponenten alle den gleichen Betrag besitzen. Durch Weglassen des Limes ist so auch ersichtlich, dass die Maximumsnorm niemals größer als die übrigen -Normen ist.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Reeller Vektor
Die 1-, 2-, 3- und ∞-Normen des reellen Vektors sind jeweils gegeben als
Komplexer Vektor
Die 1-, 2-, 3- und ∞-Normen des komplexen Vektors sind jeweils gegeben als
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Normaxiome[Bearbeiten | Quelltext bearbeiten]
Alle -Normen inklusive der Maximumsnorm erfüllen die drei Normaxiome Definitheit, absolute Homogenität und Subadditivität. Die Definitheit folgt aus der Positivität der Potenzfunktionen für positive Argumente und der Eindeutigkeit der Nullstelle an der Stelle , womit
gilt. Die Homogenität folgt aus der Homogenität der Betragsnorm über
- .
Die Dreiecksungleichung für -Normen ist gerade die Minkowski-Ungleichung
- ,
die wiederum auf der folgenden Hölder-Ungleichung basiert.
Hölder-Ungleichung[Bearbeiten | Quelltext bearbeiten]
Sind zueinander konjugierte Exponenten, das heißt mit der Konvention , dann gilt für die entsprechenden -Normen
- ,
was wiederum aus der Youngschen Ungleichung folgt. Für den Fall entspricht die Hölder-Ungleichung der Cauchy-Schwarz-Ungleichung.
Monotonie[Bearbeiten | Quelltext bearbeiten]
Die -Normen sind für einen festen Vektor und für wachsendes monoton fallend, das heißt für gilt
- .
Diese Eigenschaft folgt für und aus der Monotonie der Potenzfunktionen für durch
- ,
da der Bruch jeweils nur einen Wert zwischen Null und Eins annehmen kann. Für einen gegebenen Vektor ist damit die Summennorm die größte und die Maximumsnorm die kleinste -Norm (siehe auch die obigen Beispiele). Gleichheit über alle -Normen gilt genau dann, wenn der Vektor höchstens eine Komponente ungleich Null besitzt, also beispielsweise der Nullvektor oder der -te Einheitsvektor ist. Gleichbedeutend mit der Monotonie ist, dass sich die Einheitskugeln der -Normen für wachsendes gegenseitig enthalten, das heißt für gilt
- .
Äquivalenz[Bearbeiten | Quelltext bearbeiten]
Alle -Normen sind zueinander äquivalent, das heißt zu einem beliebigen Paar von -Normen mit gibt es zwei positive Konstanten und , sodass für alle
gilt. Die untere Konstante ist aufgrund der Monotonie immer gleich Eins. Die obere Konstante hängt von den gewählten Normen ab und wird für einen Vektor mit betragsmäßig gleichen Komponenten (etwa den Einsvektor) angenommen. Die Hölder-Ungleichung ergibt nämlich bei Wahl der Hölder-Exponenten und für
- .
Mit der Konvention im Exponenten bleibt diese Abschätzung auch für oder gültig. Die Äquivalenzkonstante der -Normen ist für in der folgenden Tabelle noch einmal zusammengefasst dargestellt:
| -Norm | -Norm | -Norm | |
|---|---|---|---|
| -Norm | |||
| -Norm | |||
| -Norm |
Hierbei ist beispielsweise der Eintrag in der ersten Zeile und zweiten Spalte für als
zu lesen. Die -Normen unterscheiden sich für einen festen Vektor somit maximal um den Faktor . Die optimalen Konstanten in solchen Normabschätzungen führen zur Berechnung von Abständen im Minkowski-Kompaktum.
Absolutheit[Bearbeiten | Quelltext bearbeiten]
Alle -Normen inklusive der Maximumsnorm sind absolut, das heißt, für alle Vektoren gilt
- ,
wobei den komponentenweisen Betrag eines Vektors darstellt.
Komponentenweise Monotonie[Bearbeiten | Quelltext bearbeiten]
Aufgrund der Absolutheit sind die -Normen für festes mit im Betrag jeder Komponente eines Vektors monoton wachsend, das heißt, es gilt
für alle mit für .[1] Für gilt sogar strenge Monotonie
für alle mit für und für mindestens ein .[2]
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]

Fall p < 1[Bearbeiten | Quelltext bearbeiten]

Die für definierte Abbildung
ist keine Norm, da die resultierende Einheitskugel nicht mehr konvex ist und somit die Dreiecksungleichung verletzt wird. Diese Abbildungen sind lediglich Quasinormen, wobei die Dreiecksungleichung durch die schwächere Ungleichung für eine reelle Konstante ersetzt wird.
ℓp-Normen[Bearbeiten | Quelltext bearbeiten]
Die -Normen sind die Verallgemeinerung der -Normen auf Folgenräume, wobei lediglich die endliche Summe durch eine unendliche ersetzt wird. Die -Norm einer in -ter Potenz betragsweise summierbaren Folge ist dann für gegeben als
- .
Für den Grenzwert ergibt sich der Raum der beschränkten Folgen mit der Supremumsnorm.
Lp-Normen[Bearbeiten | Quelltext bearbeiten]
Weiter können die -Normen auf Funktionenräume verallgemeinert werden, was in zwei Schritten geschieht. Zunächst werden die -Normen einer in -ter Potenz auf einer Menge Lebesgue-integrierbaren Funktion für als
- ,
definiert, wobei im Vergleich zu den -Normen lediglich die Summe durch ein Integral ersetzt wurde. Diese Normen sind zunächst nur Halbnormen, da nicht nur die Nullfunktion, sondern auch alle Funktionen, die sich nur an einer Menge mit Lebesgue-Maß Null von der Nullfunktion unterscheiden, zu Null integriert werden. Daher betrachtet man hier die Menge der Äquivalenzklassen von Funktionen , die fast überall gleich sind, und erhält auf diesen -Räumen die -Normen durch
- .
Für den Grenzwert ergibt sich so der Raum der wesentlich beschränkten Funktionen mit der wesentlichen Supremumsnorm. Die -Normen und -Räume lassen sich von dem Lebesgue-Maß auch auf allgemeine Maße verallgemeinern und von reell- oder komplexwertigen Funktionen auf Banachraum-wertige Funktionen, indem der Betrag durch die entsprechende Norm ersetzt wird.
Matrixnormen[Bearbeiten | Quelltext bearbeiten]
Indem eine Matrix einfach als entsprechend langer Vektor aus angesehen wird, können Matrixnormen direkt über die -Normen definiert werden. Beispiele für solche Matrixnormen sind die auf der 2-Norm basierende Frobeniusnorm und die auf der ∞-Norm basierende Gesamtnorm. Matrixnormen werden jedoch meist von einer -Norm als induzierte Matrixnorm
- .
abgeleitet. Beispiele für so definierte Matrixnormen sind die auf der 1-Norm basierende Spaltensummennorm, die auf der 2-Norm basierende Spektralnorm und die auf der ∞-Norm basierende Zeilensummennorm. Eine weitere Möglichkeit Matrixnormen zu definieren besteht darin, die -Norm des Vektors der Singulärwerte der Matrix zu betrachten, wie dies bei den Schatten--Normen der Fall ist. Auf analoge Art und Weise können auch Normen für allgemeinere lineare Operatoren definiert werden.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2008, ISBN 3-540-34186-2.
- Gene Golub, Charles van Loan: Matrix Computations. 3. Auflage. Johns Hopkins University Press, 1996, ISBN 978-0-8018-5414-9.
- Roger Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 1990, ISBN 978-0-521-38632-6.
- Hans Rudolf Schwarz, Norbert Köckler: Numerische Mathematik. 8. Auflage. Vieweg & Teubner, 2011, ISBN 978-3-8348-1551-4.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Vector Norm. In: MathWorld (englisch).
- Andrea Ambrosio, Logan Hanks, Pedro Sanchez: Vector p-norm. In: PlanetMath. (englisch)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Friedrich L. Bauer, Josef Stoer, Christoph Witzgall: Absolute and monotonic norms. In: Numerische Mathematik. Band 3, Nr. 1, 1961, S. 257–264.
- ↑ Matthias Ehrgott: Multicriteria Optimization. 2. Auflage. Springer, 2005, S. 111–113.























![{\displaystyle {\sqrt[{p}]{S}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bce901f640328d70379042645fe1bed7f6e8e811)



![{\displaystyle {\begin{aligned}\|x\|_{1}\,\,&=|3|+|{-2}|+|6|=11\\\|x\|_{2}\,\,&={\sqrt {|3|^{2}+|{-2}|^{2}+|6|^{2}}}={\sqrt {49}}=7\\\|x\|_{3}\,\,&={\sqrt[{3}]{|3|^{3}+|{-2}|^{3}+|6|^{3}}}={\sqrt[{3}]{251}}\approx 6{,}308\\\|x\|_{\infty }&=\max\{|3|,|{-2}|,|6|\}=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4630d4672323bea49d3e9d79da2c5e839aca4f54)

![{\displaystyle {\begin{aligned}\|x\|_{1}\,\,&=|3-4i|+|{-2i}|=5+2=7\\\|x\|_{2}\,\,&={\sqrt {|3-4i|^{2}+|{-2i}|^{2}}}={\sqrt {5^{2}+2^{2}}}={\sqrt {29}}\approx 5{,}385\\\|x\|_{3}\,\,&={\sqrt[{3}]{|3-4i|^{3}+|{-2i}|^{3}}}={\sqrt[{3}]{5^{3}+2^{3}}}={\sqrt[{3}]{133}}\approx 5{,}104\\\|x\|_{\infty }&=\max\{|3-4i|,|{-2i}|\}=\max\{5,2\}=5\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2503130f1075bf829f52b295f4915ca884af689)













![{\displaystyle z\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f20fead0085cbd4473680e23f8353908a40ab312)















































![{\displaystyle [f]\in L^{p}(\Omega )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/821ff5332b92210754f0b608d04b35aa7ce334a5)

![{\displaystyle \|\,[f]\,\|_{L^{p}(\Omega )}=\|f\|_{{\mathcal {L}}^{p}(\Omega )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/966f36cc30607ca13e2fb30c25894acb5dff9495)


