Polygon

Ein Polygon (von altgriechisch πολυγώνιον polygṓnion ‚Vieleck‘; aus πολύς polýs ‚viel‘ und γωνία gōnía ‚Winkel‘)[1] oder auch Vieleck ist in der elementaren Geometrie eine ebene (planare) geometrische Figur, die durch einen geschlossenen Streckenzug gebildet wird.
Ein Polygon ist ein zweidimensionales Polytop.
Ein Polygon erhält man, indem in einer Zeichenebene mindestens drei verschiedene (nicht kollineare) Punkte durch Strecken miteinander verbunden werden. Dabei entsteht ein geschlossener Streckenzug (Polygonzug) mit ebenso vielen Ecken, beispielsweise ein Dreieck (3 Punkte, 3 Strecken) oder ein Viereck (4 Punkte, 4 Strecken).
Die umschlossene Fläche wird oft auch als Polygon bezeichnet, so in der Planimetrie.
Definition und Bezeichnungen[Bearbeiten | Quelltext bearbeiten]
Ein Polygon ist eine Figur, die durch ein Tupel von verschiedenen Punkten definiert ist.
- Die Punkte heißen die Eckpunkte oder kurz Ecken des Polygons, ein Polygon mit Ecken heißt -Eck oder (insbesondere in der englischen Literatur) auch -Gon.
- Die Strecken und bezeichnet man als Seiten des Polygons.
- Alle Verbindungsstrecken zweier Eckpunkte, die keine Seiten sind, nennt man Diagonalen.
Manchmal werden noch weitere Bedingungen für die Definition eines Polygons vorausgesetzt, die aber formal nicht notwendig sind:
- Ein Polygon hat mindestens drei paarweise voneinander verschiedene Eckpunkte. Das schließt ein „Zweieck“ aus.[2]
- Drei angrenzende Eckpunkte liegen nicht auf einer Geraden. Auch , , und , , gelten dabei als angrenzende Eckpunkte. Das schließt Ecken mit gestrecktem Winkel aus.
Klassifikation[Bearbeiten | Quelltext bearbeiten]

Nach Anzahl der Ecken[Bearbeiten | Quelltext bearbeiten]
Polygone werden typischerweise nach der Zahl der Ecken (Wertigkeit des Polygons) benannt.
Regelmäßiges Polygon[Bearbeiten | Quelltext bearbeiten]
Hat ein Polygon gleiche Seiten und gleiche Innenwinkel, dann wird es als regelmäßiges Polygon oder reguläres Polygon bezeichnet. Viele regelmäßige Polygone lassen sich mit Zirkel und Lineal konstruieren (Konstruierbares Polygon).
| Ecken | Bezeichnung | Griechisch | Zirkel und Lineal |
Besonderheit |
|---|---|---|---|---|
| 3 | Dreieck | Trigon | Erste Fermatsche Primzahl 3 = 220+ 1 | |
| 4 | Viereck | Tetragon | Quadrat | |
| 5 | Fünfeck | Pentagon | Zweite Fermatsche Primzahl 5 = 221+ 1 | |
| 6 | Sechseck | Hexagon | ||
| 7 | Siebeneck | Heptagon | Siebeneck nach Archimedes (Näherungskonstruktion) | |
| 8 | Achteck | Oktogon | englisch octagon | |
| 9 | Neuneck | Nonagon | seltener Enneagon | |
| 10 | Zehneck | Dekagon | ||
| 11 | Elfeck | Hendekagon | ||
| 12 | Zwölfeck | Dodekagon | ||
| 13 | Dreizehneck | Tridekagon | ||
| 14 | Vierzehneck | Tetradekagon | ||
| 15 | Fünfzehneck | Pentadekagon | ||
| 16 | Sechzehneck | Hexadekagon | ||
| 17 | Siebzehneck | Heptadekagon | Dritte Fermatsche Primzahl 17 = 222+ 1 | |
| 18 | Achtzehneck | Oktodekagon | englisch octadecagon, octakaidecagon | |
| 19 | Neunzehneck | Nonadekagon | englisch auch enneadecagon, enneakaidecagon | |
| 20 | Zwanzigeck | Ikosagon | ||
| 21 | Einundzwanzigeck | Ikosihenagon | ||
| 22 | Zweiundzwanzigeck | Ikosidigon | ||
| 23 | Dreiundzwanzigeck | Ikositrigon | ||
| 24 | Vierundzwanzigeck | Ikositetragon | ||
| 25 | Fünfundzwanzigeck | Ikosipentagon | ||
| 26 | Sechsundzwanzigeck | Ikosihexagon | ||
| 27 | Siebenundzwanzigeck | Ikosiheptagon | ||
| 28 | Achtundzwanzigeck | Ikosioktogon | englisch icosioctagon | |
| 29 | Neunundzwanzigeck | Ikosienneagon | ||
| 30 | Dreißigeck | Triakontagon | ||
| 32 | Zweiunddreißigeck | Triakontadigon | ||
| 34 | Vierunddreißigeck | Triakontatetragon | ||
| 40 | Vierzigeck | Tetrakontagon | ||
| 48 | Achtundvierzigeck | Tetrakontaoktogon | englisch tetracontaoctagon | |
| 50 | Fünfzigeck | Pentakontagon | ||
| 51 | Einundfünfzigeck | Pentakontahenagon | ||
| 56 | Sechsundfünfzigeck | Pentakontahexagon | ||
| 60 | Sechzigeck | Hexakontagon | ||
| 64 | Vierundsechzigeck | Hexakontatetragon | ||
| 68 | Achtundsechzigeck | Hexakontaoktogon | englisch hexacontaoctagon | |
| 70 | Siebzigeck | Heptakontagon | ||
| 80 | Achtzigeck | Oktokontagon | englisch octacontagon | |
| 85 | Fünfundachtzigeck | Oktokontapentagon | englisch octacontapentagon | |
| 90 | Neunzigeck | Enneakontagon | ||
| 96 | Sechsundneunzigeck | Enneakontahexagon | ||
| 100 | Hunderteck | Hektogon | ||
| 257 | 257-Eck | Vierte Fermatsche Primzahl 257 = 223+ 1 | ||
| 1 000 | Tausendeck | Chiliagon | ||
| 10 000 | Zehntausendeck | Myriagon | ||
| 65 537 | 65 537-Eck | Fünfte Fermatsche Primzahl 65537 = 224+ 1 | ||
| 100 000 | Hunderttausendeck | |||
| 1 000 000 | Millioneck | Megagon | ||
| 4 294 967 295 | 4 294 967 295-Eck | Das Produkt aus den fünf Fermatschen Primzahlen (3 · 5 · 17 · 257 · 65537 = 4294967295 = 232 - 1) liefert die größte bekannte ungerade Eckenanzahl, die theoretisch mit Zirkel und Lineal konstruierbar ist. | ||
| 10100 | Googoleck | Googolgon | Eckenzahl: eine 1 mit 100 Nullen | |
| ∞ | Unendlicheck | Apeirogon | Theoretische Grenzform mit unendlich vielen Seiten | |
Weitere Typen[Bearbeiten | Quelltext bearbeiten]
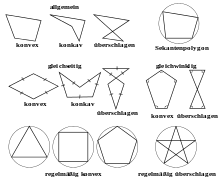
- Überschlagenes Polygon
- Bei einfachen Polygonen berühren sich die Kanten nur in den Eckpunkten; bei überschlagenen Polygonen haben die Kanten zusätzliche Schnittpunkte durch Überschneidung.
- Nicht-überschlagenes Polygon
- Nicht überschlagene Vielecke können konvex (alle Innenwinkel sind kleiner als 180°) oder nichtkonvex (mindestens ein Innenwinkel ist größer als 180°) sein.
- Nicht-planares Polygon
- Im Raum liegendes (nicht-planares) Polygon.
Polygone können gleichseitig oder gleichwinklig sein:
- Regelmäßiges Polygon
- Hat ein Polygon sowohl gleiche Seiten als auch gleiche Innenwinkel, dann wird es als regelmäßiges Polygon oder reguläres Polygon bezeichnet.
- Sternpolygon
- Planare überschlagene reguläre Polygone werden wegen ihres Aussehens auch als Sternpolygone bezeichnet.
- Orthogonales Polygon
- Bei orthogonalen Polygonen treffen alle Kanten im rechten Winkel aufeinander (das heißt, der Innenwinkel beträgt an jeder Kante entweder 90° oder 270°).
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Winkel[Bearbeiten | Quelltext bearbeiten]
In einem nicht überschlagenen, ebenen -Eck ist die Summe der Innenwinkel
- .
Für die Summe der Außenwinkel gilt dann unabhängig von der Zahl der Ecken
- .
Sind darüber hinaus alle Innen- und Außenwinkel gleich groß, so haben diese den Wert
- bzw. .
Diagonalen[Bearbeiten | Quelltext bearbeiten]
Für nicht überschlagene Polygone gilt zur Berechnung der Anzahl der Diagonalen folgende Überlegung:
- Jede der Ecken kann durch eine Strecke mit einer der anderen Ecken verbunden werden.
- Die Verbindung von Ecke zur Ecke ist mit der Verbindung von nach identisch.
- Genau Verbindungen sind Seiten des Polygons.
Also hat ein nicht überschlagenes -Eck genau Diagonalen. Bei einem nichtkonvexen Polygon gibt es (im Bereich eines überstumpfen Innenwinkels) Diagonalen außerhalb des Polygons.
Umfang[Bearbeiten | Quelltext bearbeiten]
Wenn die Eckpunkte eines ebenen einfachen Polygons durch kartesische Koordinaten gegeben sind, kann der Umfang des Polygons durch Addition der mit dem Satz des Pythagoras berechneten Seitenlängen bestimmt werden:
Fläche[Bearbeiten | Quelltext bearbeiten]
Wenn die Eckpunkte eines ebenen einfachen positiv orientierten Polygons durch kartesische Koordinaten gegeben sind, kann die Fläche des Polygons nach der gaußschen Trapezformel und deren Variationen berechnet werden:
In den Formeln gilt: .
Der Flächeninhalt von Gitterpolygonen, deren Ecken alle auf einem Gitter liegen, kann mit dem Satz von Pick berechnet werden.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Flächeninhalt[Bearbeiten | Quelltext bearbeiten]
Insbesondere für die Programmierung ist die folgende Darstellung der gaußschen Trapezformel besonders geeignet, da sich zum Speichern der Koordinaten Arrays anbieten, die Indizierung von Arrays bei vielen Programmiersprachen ohnehin bei null beginnt und die Modulo-Funktion somit besonders elegant zum Einsatz kommen kann. Die Modulo-Funktion ist hier nötig, um sogenannte Off-by-one-Fehler bei der Array-Indizierung auszuschließen. Dabei sind , , , die Koordinaten der Eckpunkte des Polygons.
Konvexe Hülle[Bearbeiten | Quelltext bearbeiten]

Algorithmen für die Ermittlung der konvexen Hülle von Punkten in der Ebene haben als untere Schranke eine asymptotische Laufzeit von . Der Beweis erfolgt durch Reduktion auf das Sortieren von Zahlen (siehe Sortierverfahren). Liegen nur der Punkte auf dem Rand der konvexen Hülle, ist die Schranke bei .
Es gibt mehrere Algorithmen zur Bestimmung der konvexen Hülle:
- Graham-Scan-Algorithmus
- Gift-Wrapping-Algorithmus
- QuickHull
- Inkrementeller Algorithmus
- Chans Algorithmus
Punkt im Polygon[Bearbeiten | Quelltext bearbeiten]

Es gibt einen einfachen Algorithmus, mit dem geprüft werden kann, ob sich ein Punkt innerhalb eines Polygons in der Ebene befindet:
Es wird ein horizontaler Strahl durch den untersuchten Punkt gelegt und untersucht, wie oft sich der Strahl mit den Kanten des Polygons schneidet. Der Punkt befindet sich innerhalb des Polygons, wenn die Anzahl der Schnittpunkte rechts vom Punkt ungerade ist. Wenn die Anzahl gerade ist, befindet sich der Punkt außerhalb.
Verwendung[Bearbeiten | Quelltext bearbeiten]
In der Informatik sind wichtige Approximationen komplexer Polygone die konvexe Hülle und das minimal umgebende Rechteck. In Algorithmen wird oft erst anhand der Approximation auf einen möglichen nichtleeren Schnitt mit einem anderen geometrischen Objekt getestet (oder dieser ausgeschlossen), erst anschließend das ganze Polygon in den Speicher geladen und ein exakter Schnitt berechnet.
In der 3D-Computergrafik werden neben anderen Verfahren der geometrischen Modellierung beliebige (auch gekrümmte) Oberflächen als Polygonnetz modelliert. Dreiecksnetze eignen sich besonders gut zur schnellen Darstellung von Oberflächen, können allerdings nicht so gut durch Subdivision Surfaces interpoliert werden. Zur Speicherung von polygonalen Netzen gibt es eine Reihe bekannter Datenstrukturen.
In der Architektur werden regelmäßige Polygone oft als Grundriss verwendet. Bekannte Beispiele:
- 5-Eck: Pentagon in Arlington, Virginia
- 8-Eck: Castel del Monte in Apulien, Italien
- 10-Eck: St. Gereon (Köln), Nordrhein-Westfalen
- 12-Eck: Saarpolygon, Steinkohlebergbau-Gedenkmonument in Ensdorf (Saar), Saarland
- 16-Eck: Leuchtturm Huisduinen bei Den Helder, Niederlande
- 18-Eck: Befreiungshalle in Kelheim, Bayern
- 30-Eck: Wiener Riesenrad in Wien, Österreich
Beispiele für Polygone im Maschinenbau[Bearbeiten | Quelltext bearbeiten]
Weiterhin wird der Begriff Polygon auch analog für die Verwendung als formschlüssige polygonale Welle-Nabe-Verbindung im Maschinenbau genutzt. Hierbei sind beliebige Polygonprofile denkbar.
Beispiele für Polygone in der Geographie[Bearbeiten | Quelltext bearbeiten]

Die Grenzen der US-Bundesstaaten Colorado und Wyoming umranden näherungsweise jeweils ein Rechteck und damit ein konvexes Polygon.
Die Staaten New Mexico und Utah haben jeweils die Form eines konkaven Polygons.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Polygon. In: MathWorld (englisch).
- Zur Mathematik unregelmäßiger Polygone
- Online-Berechnung von ebenen Polygonen mit grafischer Ausgabe
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. G. Freytag Verlag / Hölder-Pichler-Tempsky, München/Wien 1965.
- ↑ Dieter Neßelmann: 1 Ein axiomatischer Aufbau der euklidischen Geometrie, Satz 1.1.3. In: Manuskript zur Vorlesung. Universität Rostock, 22. Februar 2010, S. 4–5, abgerufen am 23. Oktober 2021.



























