Kreiseltheorie

Die Kreiseltheorie beschäftigt sich mit rotierenden Körpern, bei denen translatorische Bewegungen und Deformationen von untergeordneter Bedeutung sind. Körper, auf die diese Beschreibung zutrifft, werden in der Theorie zusammenfassend als Kreisel bezeichnet und beinhalten so verschiedene Objekte wie Spielzeugkreisel, Langgeschosse oder die Erde. Die Kreiselbewegungen sind für Mathematik, Physik und Ingenieurwesen – somit für Theorie und Praxis – gleichermaßen attraktiv. Ziel der Theorie ist es, Anwendungen auf eine sichere Grundlage zu stellen. Die Ästhetik des Gegenstands und seine anfängliche mathematische Unnahbarkeit hatte der Kreiseltheorie den Ruf einer „mathematischen Nixe“ eingetragen. Heute ist das „Kreiselproblem“ bis hin zu Detailfragen ausgelotet.

Die Kreiseltheorie definiert Eigenschaften von Kreiseln (Massenmittelpunkt, Hauptträgheitsachsen,...), deren Kinematik (Winkelgeschwindigkeit, Euler-Winkel, …) und Kinetik (Drehimpuls, Euler’sche Kreiselgleichungen,...). , leitet, auch mit dem Lagrange-Formalismus, Bewegungsfunktionen der Kreisel ab und gibt Methoden (Poinsotsche Konstruktion, Phasenraum­portraits, … ), diese anschaulich darzustellen.

Leonhard Euler begründete die (analytische) Kreiseltheorie mit den nach ihm benannten Kreiselgleichungen, die die Winkelbeschleunigungen mit den angreifenden Momenten im körperfesten Bezugssystem verbinden. Die Kreiselgleichungen sind integrabel im kräftefreien Euler-Kreisel, im schweren symmetrischen Lagrange-Kreisel, im schweren, symmetrischen, exzentrisch gelagerten Kowalewskaja-Kreisel und ansonsten nur in speziellen Kreiselbewegungen. In den integrablen Fällen hat die Winkelgeschwindigkeit einen periodischen Verlauf.

Anwendungen findet die Kreiseltheorie in der Eisenbahntechnik (Sinuslauf), der Stabilisierung von Schiffen (Schiffskreisel), Raumflugkörpern und Trägheitsnavigationssystemen sowie in der Astronomie und Ballistik.

Geschichte

Bis zu Eulers bahnbrechenden Arbeiten sind folgende Beiträge zu erwähnen:

• Archimedes gab Grundsätze über den Schwerpunkt mehrerer Größen an und formulierte Bedingungen für das statische Momentengleichgewicht.
• Johannes Kepler entdeckte 1609 die ersten beiden seiner drei Kepler’schen Gesetze, von denen das zweite eine Konsequenz der Drehimpuls­erhaltung ist.
• Isaac Newton veröffentlichte 1687 seine Prinzipia mit seinen Newton’schen Gesetzen, insbesondere formulierte er die Impulsbilanz Kraft gleich Masse mal Beschleunigung.

Leonhard Euler entwickelte 1736 eine Theorie der Präzession und 1754 den Drallsatz. Er leitete daraus seine Kreiselgleichungen her und konnte auch schon Lösungen für den kräftefreien Euler-Kreisel angeben. Joseph-Louis Lagrange leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den schweren symmetrischen Kreisel. Durch die auf der Erde allgegenwärtige Schwerkraft bekommt der Lagrange-Kreisel eine besondere Relevanz. Carl Gustav Jacob Jacobi veröffentlichte 1829 seine Theorie der elliptischen Funktionen, insbesondere der Jacobi'schen elliptischen Funktionen und der Theta-Funktionen, mit denen sich die Kreiselgleichungen lösen lassen. Sofia Kowalewskaja entdeckte 1889 den letzten durch Theta-Funktionen lösbaren Fall, den symmetrischen, schweren, exzentrisch gelagerten Kowalewskaja-Kreisel, womit die analytische Kreiseltheorie zu einem gewissen Abschluss kam. Roger Liouville zeigte 1897, dass der Euler-, Lagrange- und Kowalewskaja-Kreisel die einzigen mit algebraischen Integralen lösbaren Fälle der Kreiselgleichungen sind. Darüber hinaus können nur spezielle Bewegungen, wie beispielsweise der Fall von Goryachev-Chaplygin, integrabel sein.

Eigenschaften der Kreisel und ihrer Bewegungen

Ein Kreisel im Sinn der Kreiseltheorie ist ein beliebig gestalteter starrer Körper, der in einem Inertialsystem in einem seiner Punkte, dem Stützpunkt, derart festgehalten wird, dass er sich um diesen Punkt noch irgendwie drehen kann. Diese Forderung stellt nur eine kleine Einschränkung dar, denn jede Starrkörperbewegung lässt sich in Rotation und Translation zerlegen. Sofern letztere (näherungsweise) gleichförmig ist, spielt sie für die Kreiselbewegung keine Rolle. Es werden also auch Planeten oder der Spielzeugkreisel von der Kreiseltheorie betrachtet auch wenn dort kein Punkt fixiert ist. Von den auf den Kreisel einwirkenden äußeren Kräften ist die Schwerkraft die bei weitem wichtigste. Daher werden kräftefreie und schwere Kreisel unterschieden, je nachdem der Schwerpunkt des Kreisels im Stützpunkt liegt oder nicht.

Jeder Starrkörper hat drei ausgezeichnete Achsen, die Hauptträgheitsachsen, die paarweise zueinander senkrecht sind oder orthogonalisierbar sind. Diese Achsen bilden eine Orthonormalbasis, die kurz Hauptachsensystem genannt wird. Bezüglich dieser Achsen gleichen sich Fliehkräfte bei der Drehung genau aus und der Kreisel kann sich gleichförmig frei um sie drehen. Das Maß für den Widerstand des Kreisels gegen Bewegungsänderungen sind seine Trägheitsmomente, die bei diesen Achsen Hauptträgheitsmomente θ_1,2,3 genannt werden. Der unsymmetrische Kreisel besitzt drei verschiedene Hauptträgheitsmomente während beim symmetrischen Kreisel zwei Hauptträgheitsmomente überein stimmen. Ist das dritte Hauptträgheitsmoment größer als die beiden anderen, dann wird der Kreisel oblat genannt, anderfalls prolat.

Die Hauptträgheitsmomente sind die Eigenwerte und die Hauptträgheitsachsen ${\hat {e}}_{1,2,3}$ die dazugehörigen Eigenvektoren des Trägheitstensors, der beim rotierenden Kreisel eine vergleichbare Rolle übernimmt wie die Masse bei der Translation. In der Kreiseltheorie wird er zumeist in der Hauptachsendarstellung verwendet und kann dort mit einer Diagonalmatrix identifiziert werden. Der Trägheitstensor bildet die Winkelgeschwindigkeit auf den Drehimpuls ab. Häufig werden die Hauptträgheitmomente Θ_1,2,3 auch mit A, B und C und die Hauptachsen 1,2,3 mit ξ, η und ζ bezeichnet.

Drehgeschwindigkeit und Drehimpuls

→ Hauptartikel: Energieellipsoid

Abb. 1: Schnitt durch ein Energieellipsoid entlang zweier Hauptachse, mit den Hauptträgheitsmomenten θ₁ und θ₂

Die Winkelgeschwindigkeit lässt sich kompakt als Vektor ${\vec {\omega }}$ ausdrücken: Seine Richtung definiert die Drehachse und sein Betrag die Drehgeschwindigkeit um diese Achse. Gleiches gilt für den Drehimpuls ${\vec {L}}$, der ebenfalls Richtung und Betrag besitzt.

Die Dynamik des Kreisels lässt sich mit der Drehgeschwindigkeit und dem Drehimpuls ähnlich der Dynamik des Massenpunkts formulieren:

1. Der kräftefreie Kreisel bewegt sich so, dass sein Drehimpuls nach Betrag und Richtung konstant bleibt (so wie sich ein kräftefreier Massenpunkt gleichförmig bewegt).
2. Unter dem Einfluss von Drehmomenten bewegt sich der Kreisel derart, dass die Änderungsgeschwindigkeit des Drehimpulsvektors nach Richtung und Betrag gleich dem angreifenden Moment ist (so wie die Beschleunigung des Massenpunkts in Richtung einer angreifenden Kraft erfolgt). Das ist die Aussage des Drallsatzes, auf den unten näher eingegangen wird.

Wird der Drehimpuls im körperfesten Hauptachsensystem ausgedrückt, dann sind die Komponenten in Richtung der Hauptachsen mit den größten Hauptträgheitsmomenten gegenüber den Drehgeschwindigkeitskomponenten betont. Die Richtung des Drehimpulses liegt daher immer irgendwo zwischen der Drehachse und den Hauptachsen mit den größten Hauptträgheitsmomenten.

In Abb. 1 ist ein Schnitt durch ein Energieellipsoid zu sehen, das die Menge aller Winkelgeschwindigkeiten ist, die bei einem gegebenen Kreisel zur selben Rotationsenergie führen. Die Richtung des Drehimpulses steht immer senkrecht auf dem Energieellipsoid in dem Punkt, wo die aktuelle Winkelgeschwindigkeit dieses berührt. Die Länge der Halbachsen des Ellipsoids sind umgekehrt proportional zu den Hauptträgheitsmomenten: Das Hauptträgheitsmoment in horizontaler Richtung ist im Bild kleiner als das in vertikaler. Daher ist der Drehimpuls im Bild steiler ausgerichtet als die Winkelgeschwindigkeit. Nur bei Drehungen um eine der Hauptachsen sind Drehimpuls und Winkelgeschwindigkeit parallel. Liegt die Drehachse hingegen dazwischen, schließen sie einen spitzen Winkel ein.

Präzession und Nutation des symmetrischen Kreisels

Abb. 2: Bewegungsform eines symmetrischen, oblaten, kräftefreien Kreisels

Rotiert der symmetrische Kreisel nicht nur um seine Figurenachse, dann fallen Drehimpuls und Winkelgeschwindigkeit nicht zusammen und die Figurenachse vollführt eine Bewegung im Raum, siehe Abb. 2. Diese Bewegung wird in der Kreiseltheorie Nutation genannt. Die Figurenachse ist eine körperfeste Linie.

Die Drehachse eines Kreisels hingegen ist keine körperfeste Linie, sie kann sich also relativ zum Kreisel bewegen. Diese Relativbewegung der Drehachse wird Präzession genannt und kann mit oder ohne Krafteinwirkung auftreten, in letzterem Fall, wenn sich der Kreisel nicht um eine seiner Hauptachsen dreht, siehe Abb. 2. Bei der Präzession des kräfefreien symmetrischen Kreisels beschreibt die Drehachse einen Kegel, den Gangpolkegel, mit konstantem Öffnungswinkel um die Figurenachse. Diese reguläre Präzession kann auch beim schweren Kreisel als Sonderfall auftreten.

Wenn der schwere Kreisel die speziellen Bedingungen der regulären Präzession nicht erfüllt, dann pendelt der Winkel zwischen Figuren- und Drehachse zwischen zwei Extremwerten hin und her. Diese Bewegung wird auch, insbesondere in der Astronomie, Nutation genannt. Je größer das Verhältnis zwischen Rotations- und Lageenergie des Kreisels ist, desto enger liegen diese beiden Extremwerte zusammen, und das kann so weit gehen, dass das Pendeln zwischen den Extremwerten mit den Augen nicht mehr wahrnehmbar ist. Die Präzession sieht dann aus wie eine reguläre Präzession, ist aber keine, und wird pseudoreguläre Präzession genannt.

Drallsatz

→ Hauptartikel: Drehimpuls

Abb. 3: Zur Regel vom gleichsinnigen Parallelismus

Das in der Kreiseltheorie wichtigste physikalische Gesetz ist der Drallsatz, der sich beim Kreisel als Regel vom gleichsinnigen Parallelismus ausdrückt, siehe Abb. 3.: Greift am Kreisel ein Drehmoment an, dann versucht der Kreisel seine Drehbewegung dem Drehsinn des Moments gleichsinnig parallel auszurichten, was im Bild blau angedeutet ist. Aus diesem Grundsatz leiten sich viele Eigenschaften der Kreiselbewegungen ab. Wirkt auf den Kreisel beispielsweise eine Kraft, dann ist das von ihr ausgeübte Drehmoment senkrecht zu ihr und somit weicht ein rotierender Kreisel einer Kraft immer senkrecht zu ihrer Wirkungsline aus.

Der Drallsatze besagt, dass um den Drehimpuls eines Kreisels zu verändern, ein Drehmoment angreifen muss. Ohne solche Momente bleibt der Drehimpuls in Betrag und Richtung erhalten. Die mathematische Formulierung lautet:

${\vec {M}}={\dot {\vec {L}}}$

Darin ist ${\vec {M}}$ das am Kreisel angreifende Drehmoment, ${\vec {L}}$ der Drehimpuls des Kreisels und ${\dot {\vec {L}}}$ seine zeitliche Änderung. Aus dem Drallsatz leiten sich auch die Euler’schen Kreiselgleichungen ab, mit denen die genaue rechnerische Behandlung der Kreiselbewegungen erfolgt, siehe unten.

Der Drehimpuls und die Drehachse sind – wie oben berichtet – nur bei Drehungen um eine der Hauptachsen parallel. In den anderen Fällen gilt:

• Bei konstantem Drehimpuls ändert sich bei freier Bewegung fortlaufend die Drehachse und der Kreisel taumelt oder „eiert“.
• Wird die Drehachse festgehalten, dann ändert sich fortlaufend der Drehimpuls, mit den Konsequenzen:
  • Die Halterungen der Drehachse müssen die dazu notwendigen Momente einbringen.
  • Umgekehrt werden die Halterungen durch die Reaktionsmomente belastet und müssen diese abtragen.

Kreiselwirkung

→ Hauptartikel: Gyroskopischer Effekt

Das auffälligste Merkmal von symmetrischen Kreiseln ist die des gyroskopischen Effekts oder der Kreiselwirkung, die die Drehung um die Figurenachse abhängig von der Drehzahl stabilisiert und die in technischen Anwendungen ausgenutzt wird.

Die Kreiselwirkung ${\vec {K}}$ ist eine d’Alembertsche Trägheitskraft und als solche ein einem angreifenden Moment ${\vec {M}}$ entgegengesetzt gleichgroßes Moment:

${\vec {K}}=-{\vec {M}}$

Moment und Kreiselwirkung befinden sich im dynamischen Gleichgewicht. Somit entspricht die Kreiselwirkung der negativen Drehimpulsänderung und ist gleich der Summe der Kreiselwirkungen der Euler- und Zentrifugalkräfte im Körper:

${\vec {K}}={\vec {K}}_{\rm {Euler}}+{\vec {K}}_{\rm {Zentrifugal}}=-{\dot {\vec {L}}}$.

Abb. 4: Schwungrad zur Erläuterung der Kreiselwirkung

Um die Kreiselwirkung zu erläutern, wird die Bewegung des Schwungrads in Abb. 4 betrachtet, wobei die Figurenachse (y-Richtung) frei ist, so dass sie ihre Richtung beliebig ändern kann. Auf dieses ansonsten kräftefreie Schwungrad wirke eine kurze Zeit in z-Richtung ein kleines konstantes Moment M_z, das das Schwungrad in Drehung um z versetzt. Diese Drehung macht sich am ruhenden und rotierenden Schwungrad jedoch unterschiedlich bemerkbar:

1. Ruht das Schwungrad, dann beginnt es durch das Moment um z zu rotieren. Nachdem das Moment aufgehört hat zu wirken, verharrt das Schwungrad in der Drehung um z, es gibt keine Kreiselwirkung und der Drehwinkel ψ der Figurenachse um z nimmt monoton zu und ist unbeschränkt. Die Winkelgeschwindigkeit und der Drehimpuls haben nur eine Komponente und die weist in z-Richtung. Der Neigungswinkel ϑ zwischen Figurenachse und Momentenachse z bleibt unverändert.
2. Rotiert das Schwungrad anfänglich hinreichend schnell um die Figurenachse, dann zeigt sich ein anderes Bild. Zwar führt das Moment auch hier zu einer linearen Zunahme des Drehimpulses in z-Richtung, aber weil sich diese (als klein angenommene) Komponente zum anfänglichen Drehimpuls in y-Richtung vektoriell addiert, und Drehimpuls und Winkelgeschwindigkeit einen spitzen Winkel einschließen (siehe oben), dreht das Schwungrad weiter vor allem um die y-Achse. Dadurch bleibt der Drehwinkel ψ der Figurenachse um z beschränkt. Nach der Regel des gleichsinnigen Parallelismus versucht der Kreisel seine Drehung dem angreifenden Moment anzugleichen, wodurch der Winkel ϑ abnimmt.

Ursache für den geringen Einfluss des Moments auf die Drehung des rotierenden Schwungrads um z sind Trägheitskräfte, die, wie im Folgenden geschildert, Gegenmomente aufbauen. Dabei wird der übliche Fall voraus gesetzt, dass das Schwungrad ein oblater Kreisel ist, sein Trägheitsmoment B um die Figurenachse also größer ist als die äquatorialen Trägheitsmomente A. Anderfalls wären die Kreiselwirkungen in x-Richtung umgekehrt orientiert. Anders als im Bild soll der Winkel ψ von der y-Achse aus zählen und es wird die weiter unten begründete Näherung M = L ω benutzt, dergemäß ein Moment M zur Drehgeschwindigkeit ω eines zu ihm senkrechten Drehimpulses L führt.

1. Das kleine Moment M_z dreht das Schwungrad mit Drehimpuls L in y-Richtung zunächst (langsam) um die z-Achse und der Winkel ψ nimmt gemäß der Beschleunigungsgleichung $A{\ddot {\psi }}=M_{z}$ zu. Der Beschleunigungsterm $A{\ddot {\psi }}$ ist eine Kreiselwirkung in -z-Richtung, die sich aus Euler-Kräften speist.
2. So bekommt die Winkelgeschwindigkeit eine kleine Komponente in z-Richtung und die Neigung ϑ der Drehachse gegenüber der Vertikalen verringert sich entsprechend $A{\ddot {\vartheta }}=-L{\dot {\psi }}\rightarrow {\dot {\vartheta }}=-{\tfrac {L}{A}}\psi$. Diese Winkelbeschleunigung um x zieht Euler-Kräfte nach sich, die in Summe eine Kreiselwirkung in -x-Richtung hervor bringen.
3. In gleicher Weise wie das Moment M_z die Kreiselwirkung in -x-Richtung hervor ruft, so entsteht durch letztere eine weitere Kreiselwirkung $L{\dot {\vartheta }}=-{\tfrac {L^{2}}{A}}\psi$ in -z-Richtung, die der Beschleunigungsgleichung im ersten Schritt hinzu zu fügen ist: $A{\ddot {\psi }}=M_{z}-{\tfrac {L^{2}}{A}}\psi$.
4. Ganz analog wie das Moment M_z eine entgegengesetzte Kreiselwirkung auslöst, besitzt auch die Kreiselwirkung in -x-Richtung eine Widersacherin in +x-Richtung, die sich aus den Zentrifugalkräften im Schwungrad speist.

Während sich die Kreiselwirkungen in -z-Richtung ($A{\ddot {\psi }}$ und ${\tfrac {L^{2}}{A}}\psi$) genau zu M_z summieren, löschen sich die Kreiselwirkungen in x- und y-Richtung genau aus. Das Moment der Euler-Kräfte ist dort antiparallel zum Moment der Zentrifugalkräfte. Auf diese Weise bleiben die Drehimpulse in x- und y-Richtung gegenüber dem Anfangszustand unverändert.

Die im dritten Schritt erhaltene Gleichung für die Winkelbeschleunigung ${\ddot {\psi }}$ ist eine Schwingungsgleichung, weswegen die Figurenachse unter dem Moment in z-Richtung eine Schwingung um z ausführt. Mit dem konstanten Drehimpuls $L=B{\dot {\varphi }}$ in y-Richtung lautet die Schwingungsgleichung

${\frac {M_{z}}{A}}={\ddot {\psi }}+\left({\frac {B}{A}}{\dot {\varphi }}\right)^{2}\psi$

Darin ist φ der Drehwinkel um die Figurenachse. Die Eigenkreisfrequenz der Schwingung der Figurenachse um die z-Achse ist demnach proportional zum Verhältnis der Trägheitsmomente und zur Winkelgeschwindigkeit um die Figurenachse. Die Schwingungsgleichung ist eine Näherung, die nur bei kleiner Auslenkung ψ gültig ist.

Für die stabilisierende Kreiselwirkung ist dabei die freie Drehungsmöglichkeit der Figurenachse um die äquatorialen Achsen entscheidend. Wird die Drehachse durch Lager an die xy-Ebene gebunden, können die Momente der Trägheitskräfte nicht ihr Potenzial entfalten und es tritt keine Kreiselwirkung auf.

Kinematik von Kreiseln

Die Kinematik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die nicht von der Masse abhängen.

Bezugssysteme

→ Hauptartikel: Bezugssystem

In der Kreiseltheorie werden vor allem drei Bezugssysteme verwendet:

Im Inertialsystem, in dem der Stützpunkt ruht und der Kreisel rotiert, werden die Euler-Winkel definiert, die die Position des Kreisels, also die Orientierung seiner Hauptachsen, im Raum angeben. Der zeitliche Verlauf der Winkel bestimmt dann die Bewegungsfunktion des Kreisels. In diesem System sind die Massenträgheitsmomente um nicht festgehaltene Achsen zeitlich variabel.

Im mitrotierenden körperfesten Bezugssystem sind die Bewegungsgleichungen besonders leicht zu formulieren, denn nur dort sind die Trägheitsmomente zeitlich konstant. Die Bewegung wird hier durch zusätzlich wirkende Trägheitskräfte beeinflusst. Diese sind die Euler-Kraft und die Fliehkraft. Corioliskräfte können nicht auftreten, weil beim Starrkörper eine Bewegung seiner Massenpunkte relativ zum Körper ausgeschlossen ist.

Gelegentlich wird bei symmetrischen Kreiseln noch ein anschauliches System verwendet, bei dem eine Achse mit der Figurenachse übereinstimmt, die anderen Achsen aber an der Rotation nicht teilnehmen. Hier wirken dann alle drei Formen der Trägheitskräfte: Euler-, Flieh- und Corioliskraft.

Die Bezugssysteme stellen sich mathematisch als Basisvektoren ${\hat {e}}_{1,2,3}$ dar, mit denen vektorielle Größen ausgedrückt werden. Die Zeitableitung solcher vektorieller Größen, beispielsweise des Wegs ${\vec {r}}$, teilt sich im rotierenden Bezugssystem auf in einen Anteil, der auf die Relativbewegung im Bezugssystem zurück geht, und einen zusätzlichen, der durch die Rotation des Bezugssystems beigetragen wird:

${\begin{aligned}{\dot {\vec {r}}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\sum _{i=1}^{3}r_{i}{\hat {e}}_{i}=\sum _{i=1}^{3}{\dot {r}}_{i}{\hat {e}}_{i}+\sum _{i=1}^{3}r_{i}{\dot {\hat {e}}}_{i}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {r}}+{\vec {\omega }}\times {\vec {r}}\end{aligned}}$

Darin ist ${\tfrac {\mathrm {d} '}{\mathrm {d} t}}$ die „relative Zeitableitung“, die auch als ${\tfrac {\mathrm {d} _{r}}{\mathrm {d} t}}$ notiert wird und bei der die Basisvektoren des Bezugssystems als konstant angenommen werden. Der Vektor ${\vec {\omega }}$ ist die Winkelgeschwindigkeit und × bildet das Kreuzprodukt.

Winkelgeschwindigkeit

→ Hauptartikel: Winkelgeschwindigkeit

Mit der Winkelgeschwindigkeit berechnen sich die Raten der rotierenden Hauptachsen:

${\dot {\hat {e}}}_{i}:={\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {e}}_{i}={\vec {\omega }}\times {\hat {e}}_{i}$

Darin stehen ${\hat {e}}_{1,2,3}$ für das körperfeste, mitrotierende Hauptachsensystem. Deshalb stimmen bei der Winkelgeschwindigkeit die Zeitableitung und die relative Zeitableitung im Hauptachsensystem überein:

${\dot {\vec {\omega }}}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {\omega }}+{\vec {\omega }}\times {\vec {\omega }}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {\omega }}=\sum _{i=1}^{3}{\dot {\omega }}_{i}{\hat {e}}_{i}$

Häufig werden die Komponenten ω_1,2,3 im Hauptachsensystem auch mit p, q und r bezeichnet.

Eulersche Geschwindigkeitsgleichung

Die allgemeine Bewegung starrer Körper ist durch die eulersche Geschwindigkeitsgleichung

${\vec {v}}({\vec {x}},t)={\dot {\vec {b}}}(t)+{\vec {\omega }}(t)\times ({\vec {x}}-{\vec {b}}(t))$

gegeben. Sie gibt zur Zeit t am Ort ${\vec {x}}$ die Geschwindigkeit ${\vec {v}}$ eines Partikels an, die sich aus der Bewegung eines Bezugspunkts ${\vec {b}}(t)$ und einer Drehung um ihn mit Winkelgeschwindigkeit ${\vec {\omega }}(t)$ zusammen setzt. In der Kreiseltheorie wird der Punkt ${\vec {b}}$ festgehalten und in den Ursprung eines Koordinatensystems gelegt, sodass ${\vec {b}}\equiv {\vec {0}}$ und die Geschwindigkeitsverteilung

${\vec {v}}({\vec {x}},t)={\vec {\omega }}(t)\times {\vec {x}}\,.$

gilt. Alle Partikel des Kreisels, die sich auf der Drehachse befinden (für die ist ${\vec {x}}\parallel {\vec {\omega }}$), ruhen solange sie das tun. Da die Drehachse nicht an die Partikel des Kreisels gebunden ist, kann sich die Drehachse relativ zum Kreisel bewegen, was eine wichtige Eigenschaft der Kreiselbewegung ist, die Präzession genannt wird.

Alle Massenträgheitsmomente und Drehmomente werden in der Kreiseltheorie immer bezüglich des Stützpunkts aufgestellt.

Euler-Winkel

→ Hauptartikel: Euler-Winkel

Abb. 5: Das eulersche Basissystem (grün) gibt die Achsen an, um die die Euler-Winkel α, β und γ drehen.

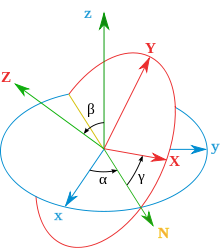
Die Beschreibung der Basisvektoren im raumfesten Bezugssystem gelingt mit den Euler’schen Winkeln, beispielsweise in der Standard-x-Konvention (z, x', z"), siehe Abb. 5. Bezeichnen die Einheitsvektoren ${\hat {e}}_{x,y,z}$ die raumfeste Standardbasis (blau in Abb. 5) und ${\hat {e}}_{X,Y,Z}={\hat {e}}_{1,2,3}$ die mit dem Körper rotierende, bewegte Basis (rot in Abb. 5), dann lauten die mitbewegten Basisvektoren bezüglich der raumfesten Basis:

${\begin{aligned}{\hat {e}}_{1}=&{\begin{pmatrix}\cos(\alpha )\cos(\gamma )-\sin(\alpha )\cos(\beta )\sin(\gamma )\\\sin(\alpha )\cos(\gamma )+\cos(\alpha )\cos(\beta )\sin(\gamma )\\\sin(\beta )\sin(\gamma )\end{pmatrix}}\\{\hat {e}}_{2}=&{\begin{pmatrix}-\cos(\alpha )\sin(\gamma )-\sin(\alpha )\cos(\beta )\cos(\gamma )\\-\sin(\alpha )\sin(\gamma )+\cos(\alpha )\cos(\beta )\cos(\gamma )\\\sin(\beta )\cos(\gamma )\end{pmatrix}}\\{\hat {e}}_{3}=&{\begin{pmatrix}\sin(\alpha )\sin(\beta )\\-\cos(\alpha )\sin(\beta )\\\cos(\beta )\end{pmatrix}}\,.\end{aligned}}$

Der Zusammenhang mit den Winkelgeschwindigkeiten ist

${\begin{aligned}\omega _{1}=&{\dot {\alpha }}\sin(\beta )\sin(\gamma )+{\dot {\beta }}\cos(\gamma )\\\omega _{2}=&{\dot {\alpha }}\sin(\beta )\cos(\gamma )-{\dot {\beta }}\sin(\gamma )\\\omega _{3}=&{\dot {\alpha }}\cos(\beta )+{\dot {\gamma }}\\{\dot {\alpha }}=&{\frac {\omega _{1}\sin(\gamma )+\omega _{2}\cos(\gamma )}{\sin(\beta )}}\\{\dot {\beta }}=&\omega _{1}\cos(\gamma )-\omega _{2}\sin(\gamma )\\{\dot {\gamma }}=&\omega _{3}-{\dot {\alpha }}\cos(\beta )\end{aligned}}$

Bei β = 0 tritt eine Singularität auf, weil dann die Winkel α und γ in den Basisvektoren nur als Summe α + γ vorkommen und somit verschiedene Winkel zur selben Basis führen können.

Freiheitsgrade des Kreisels

Der rotierende Kreisel besitzt fünf Freiheitsgrade: drei Winkel und die Position des Schwerpunkts relativ zum Stützpunkt, wobei der Abstand zwischen Schwer- und Stützpunkt konstant ist. Sind also fünf unabhängige Erhaltungsgrößen der Kreiselbewegung gefunden, dann ist die Bewegungsgleichung gelöst. Es genügen sogar nur vier, denn mit der Jacobi'schen Multiplikatoren Methode kann aus vier unabhängigen Integralen ein fünftes konstruiert werden.

Kinetik von Kreiseln

Die Kinetik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die von der Masse abhängen.

Trägheitstensor, Hauptträgheitmomente und Hauptachsen

→ Hauptartikel: Trägheitstensor

Der Trägheitstensor ist ein Maß für den Widerstand des Kreisels gegen Änderungen seines Drehimpulses und deshalb eine zentrale Größe in der Kreiseltheorie. Bei einem aus einzelnen Massenpunkten aufgebauten starren Körper berechnet er sich aus der Summe

$\mathbf {\Theta } :=\sum _{i}m_{i}[({\vec {r}}_{i}\cdot {\vec {r}}_{i})\mathbf {1} -{\vec {r}}_{i}\otimes {\vec {r}}_{i}]=\sum _{i,j=1}^{3}\Theta _{ij}{\hat {g}}_{i}\otimes {\hat {g}}_{j}=\sum _{i=1}^{3}\Theta _{i}{\hat {e}}_{i}\otimes {\hat {e}}_{j}$

Die Vektoren ${\vec {r}}_{i}$ bezeichnen die aktuelle Position des i-ten Massenpunkts, m_i dessen Masse, ${\hat {g}}_{1,2,3}$ eine beliebige Basis, das Rechenzeichen „·“ bildet das Skalarprodukt, ⊗ das dyadischen Produkt von Vektoren und 1 ist der Einheitstensor. Die Komponenten Θ_ij des Trägheitstensors sind in einem körperfesten System konstant, im Inertialsystem, in dem sich der Kreisel dreht, jedoch zeitabhängig. Die letzte Darstellung zeigt den Trägheitstensor in seiner Hauptachsendarstellung mit Hauptträgheitmomenten Θ_1,2,3 und Hauptträgheitsachsen oder kurz Hauptachsen ${\hat {e}}_{1,2,3}$. Die Hauptachsen sind körperfest und drehen mit dem Kreisel mit. Der Trägheitstensor ist symmetrisch und positiv definit.

Drehimpuls von Kreiseln

Bei einem aus einzelnen Massenpunkten aufgebauten starren Körper kann mit obiger Geschwindigkeitsverteilung der Eigen­drehimpuls relativ zum Stützpunkt als Summe berechnet werden:

${\vec {L}}:=\sum _{i}{\vec {r}}_{i}\times {\vec {p}}_{i}=\sum _{i}m_{i}{\vec {r}}_{i}\times ({\vec {\omega }}\times {\vec {r}}_{i})=\mathbf {\Theta } \cdot {\vec {\omega }}$

Die Summe ist über alle Massenpunkte zu erstrecken, deren Position relativ zum Stützpunkt darin mit ${\vec {r}}_{i}$ bezeichnet wird und ${\vec {p}}_{i}=m_{i}{\vec {v}}_{i}=m_{i}{\vec {\omega }}\times {\vec {r}}_{i}$ ist der aktuelle Impuls des Massenpunkts. Ein Vergleich von ${\vec {p}}=m{\vec {v}}$ mit ${\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}$ zeigt, dass der Trägheitstensor für Drehungen eine vergleichbare Rolle wie die Masse für Translationsbewegungen spielt.

Mechanische Energie von Kreiseln

Bei einem aus einzelnen Massenpunkten aufgebauten starren Körper ergibt sich mit obiger Geschwindigkeitsverteilung die Rotationsenergie

${\begin{aligned}E_{\rm {rot}}:=&{\frac {1}{2}}\sum _{i}m_{i}{\vec {v}}({\vec {r}}_{i},t)^{2}={\frac {1}{2}}\sum _{i}m_{i}({\vec {\omega }}\times {\vec {r}}_{i})^{2}\\=&{\frac {1}{2}}{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {1}{2}}{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}={\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}\end{aligned}}$

Weil also das Skalarprodukt von Winkelgeschwindigkeit und Drehimpuls bei einer Drehung immer positiv ist, schließen sie immer einen spitzen Winkel ein. In einem Schwerefeld mit Schwerebeschleunigung ${\vec {g}}$ besitzt der Starrkörper die Lageenergie

$E_{\rm {pot}}=-\sum _{i}m_{i}({\vec {r}}_{i}\cdot {\vec {g}})=-{\vec {g}}\cdot \sum _{i}m_{i}{\vec {r}}_{i}=-m{\vec {g}}\cdot {\vec {s}}$

Darin ist $\textstyle m:=\sum _{i}m_{i}$ die Masse und $\textstyle {\vec {s}}:={\tfrac {1}{m}}\sum _{i}m_{i}{\vec {r}}_{i}$ der Massenmittelpunkt des Starrkörpers relativ zum Stützpunkt. Die Lageenergie nimmt also entgegen der Schwerebeschleunigung, im Schwerefeld der Erde also mit der Höhe, zu. Im körperfesten Hauptachsensystem haben die Schwerebeschleunigung und der Massenmittelpunkt die Koordinaten:

${\begin{aligned}{\vec {g}}=&g(n_{1}{\hat {e}}_{1}+n_{2}{\hat {e}}_{2}+n_{3}{\hat {e}}_{3}),\quad g=|{\vec {g}}|\\{\vec {s}}=&s_{1}{\hat {e}}_{1}+s_{2}{\hat {e}}_{2}+s_{3}{\hat {e}}_{3}\end{aligned}}$

mit Konstanten s_1,2,3 im Hauptachsensystem. Damit lautet die Lageenergie

$E_{\rm {pot}}=-m{\vec {g}}\cdot {\vec {s}}=-mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

In der Literatur werden die Komponenten n_1,2,3 der Schwerkraftrichtung auch mit γ, γ', γ'' bezeichnet. Wenn der Schwerpunkt der Stützpunkt ist (${\vec {s}}={\vec {0}}$), dann hat die Schwerebeschleunigung keinen Einfluss auf die Bewegung des Kreisels, was beim eulerschen Kreisel der Fall ist. Im Gegensatz dazu liegt beim schweren Kreisel der Schwerpunkt nicht im Stützpunkt und das Schwerefeld beeinflusst die Kreiselbewegung durch ein Moment

${\vec {M}}={\vec {s}}\times m{\vec {g}}=mg{\begin{pmatrix}s_{2}n_{3}-s_{3}n_{2}\\s_{3}n_{1}-s_{1}n_{3}\\s_{1}n_{2}-s_{2}n_{1}\end{pmatrix}}$

Die letzte Darstellung als Spaltenvektor bezieht sich auf das Hauptachsensystem und das soll auch im Folgenden gelten.

Schranken für Drehimpuls und Rotationsenergie

Der Drehbewegung eines Kreisels kann jederzeit zum einen ein Drehimpuls­betrag $L:=|{\vec {L}}|$ und zum anderen eine Rotationsenergie $E_{\mathrm {rot} }$ zugeordnet werden. Bei einem Kreisel liegen diese beiden Größen innerhalb der Schranken

$2\Theta _{1}E_{\rm {rot}}\leq L^{2}\leq 2\Theta _{3}E_{\rm {rot}}$ oder ${\frac {L^{2}}{2\Theta _{3}}}\leq E_{\rm {rot}}\leq {\frac {L^{2}}{2\Theta _{1}}}$

Darin wurde die übliche Anordnung Θ₁ < Θ₂ < Θ₃ der Hauptträgheitsmomente voraus gesetzt.

Denn im lokalen körperfesten Hauptachsensystem ausgedrückt gilt:

${\begin{aligned}L^{2}&=&(\mathbf {\Theta } \cdot {\vec {\omega }})\cdot (\mathbf {\Theta } \cdot {\vec {\omega }})&=&\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\\2E_{\mathrm {rot} }&=&{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}&=&\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2}\end{aligned}}$

Diese beiden Gleichungen stellen mathematisch Ellipsoide dar, die erste das Drallellipsoid, die zweite das Energieellipsoid, die im kräfefreien Fall – und nur dort – gleichbleibende Ausdehnung besitzen. Ein Punkt, der auf beiden Ellipsoiden liegt, muss die Bedingungen

${\begin{aligned}1=&{\frac {1}{L^{2}}}(\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2})={\frac {1}{2E_{\rm {rot}}}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})\\\rightarrow 0=&(2E_{\rm {rot}}\Theta _{1}-L^{2})\Theta _{1}\omega _{1}^{2}+(2E_{\rm {rot}}\Theta _{2}-L^{2})\Theta _{2}\omega _{2}^{2}+(2E_{\rm {rot}}\Theta _{3}-L^{2})\Theta _{3}\omega _{3}^{2}\\=&2\left(E_{\rm {rot}}-{\frac {L^{2}}{2\Theta _{1}}}\right)\Theta _{1}^{2}\omega _{1}^{2}+2\left(E_{\rm {rot}}-{\frac {L^{2}}{2\Theta _{2}}}\right)\Theta _{2}^{2}\omega _{2}^{2}+2\left(E_{\rm {rot}}-{\frac {L^{2}}{2\Theta _{3}}}\right)\Theta _{3}^{2}\omega _{3}^{2}\end{aligned}}$

erfüllen. In den letzten beiden Gleichungen sind alle Faktoren bis auf die Klammerausdrücke null oder positiv. Eine nicht-triviale Lösung existiert, wenn in den Gleichungen der kleinste Klammerausdruck nicht positiv und der größte nicht negativ ist. Mit den angenommenen Größenverhältnissen der Hauptträgheitsmomente stellen dies die obigen Schranken für das Drehimpulsbetragsquadrat und die Rotationsenergie sicher. Dann sind die Rotationsenergie und der Drehimpulsbetrag mit einer Drehbewegung des betrachteten Körpers verträglich.

Eulersche Kreiselgleichungen

Die Euler’schen Kreiselgleichungen ergeben sich aus dem Drallsatz

${\vec {M}}={\dot {\vec {L}}}=\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}+{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {L}}+{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\times {\vec {L}}$

Im körperfesten Hauptachsensystem lauten die Kreiselgleichungen ausgeschrieben:

${\begin{aligned}M_{1}=&\Theta _{1}{\dot {\omega }}_{1}+(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}={\dot {L}}_{1}+\left({\frac {1}{\Theta _{2}}}-{\frac {1}{\Theta _{3}}}\right)L_{2}L_{3}\\M_{2}=&\Theta _{2}{\dot {\omega }}_{2}+(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}={\dot {L}}_{2}+\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{1}}}\right)L_{3}L_{1}\\M_{3}=&\Theta _{3}{\dot {\omega }}_{3}+(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}={\dot {L}}_{3}+\left({\frac {1}{\Theta _{1}}}-{\frac {1}{\Theta _{2}}}\right)L_{1}L_{2}\end{aligned}}$

Darin sind jeweils für k=1,2,3

M_k die von außen angreifenden Drehmomente,

Θ_k die Hauptträgheitmomente,

L_k := Θ_kω_k die Drehimpulse,

ω_k die Winkelgeschwindigkeiten und

${\dot {\omega }}_{k}$ die Winkelbeschleunigungen

im Hauptachsensystem. Die Terme auf der rechten Seite stehen für Trägheitseffekte im beschleunigten Bezugssystem:

${\begin{aligned}{\vec {K}}_{\rm {Euler}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\dot {\vec {\omega }}}\times {\vec {r}}_{i}]=-\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}=-{\begin{pmatrix}\Theta _{1}{\dot {\omega }}_{1}\\\Theta _{2}{\dot {\omega }}_{2}\\\Theta _{3}{\dot {\omega }}_{3}\end{pmatrix}}\\{\vec {K}}_{\rm {Zentrifugal}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}_{i})]=-{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}=-{\begin{pmatrix}(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}\\(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}\\(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}\end{pmatrix}}\end{aligned}}$

Die Vektoren in den eckigen Klammern stellen in der oberen Gleichung die Euler-Kraft und unten die Zentrifugalkraft am Massenpunkt im Ort ${\vec {r}}_{i}$ und Masse m_i im rotierenden Bezugssystem dar. Diese Kreiselwirkungen befinden sich im dynamischen Gleichgewicht mit dem äußeren Moment: ${\vec {M}}+{\vec {K}}_{\rm {Euler}}+{\vec {K}}_{\rm {Zentrifugal}}={\vec {0}}$. In den Richtungen senkrecht zum angreifenden Moment neutralisieren sich die Kreiselwirkungen der Euler- und Zentrifugalkräfte und befinden sich dort somit untereinander im dynamischen Gleichgewicht.

Euler-Poisson Gleichungen

Die Euler-Poisson Gleichungen sind die spezifischen Kreiselgleichungen für den schweren Kreisel. Dieser wurde von Joseph-Louis Lagrange und erst ein wenig später von Siméon Denis Poisson analytisch gelöst. Trotzdem sind die Gleichungen nach Poisson benannt und lauten

${\begin{aligned}{\vec {s}}\times m{\vec {g}}=&\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}+{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}\\{\vec {0}}=&{\dot {\vec {g}}}={\frac {\mathrm {d} '{\vec {g}}}{\mathrm {d} t}}+{\vec {\omega }}\times {\vec {g}}\end{aligned}}$

Oder in Komponenten:

${\begin{aligned}mg(s_{2}n_{3}-s_{3}n_{2})=&\Theta _{1}{\dot {\omega }}_{1}+(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}\\mg(s_{3}n_{1}-s_{1}n_{3})=&\Theta _{2}{\dot {\omega }}_{2}+(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}\\mg(s_{1}n_{2}-s_{2}n_{1})=&\Theta _{3}{\dot {\omega }}_{3}+(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}.\\{\dot {n}}_{1}=&\omega _{3}n_{2}-\omega _{2}n_{3}\\{\dot {n}}_{2}=&\omega _{1}n_{3}-\omega _{3}n_{1}\\{\dot {n}}_{3}=&\omega _{2}n_{1}-\omega _{1}n_{2}\end{aligned}}$

Lagrange- und Hamiltonfunktion des Kreisels

Die Lagrangefunktion des Kreisels ist die Differenz der Rotationsenergie und der potentiellen Energie

${\mathcal {L}}=E_{\rm {rot}}-E_{\rm {pot}}={\frac {L_{1}^{2}}{2\Theta _{1}}}+{\frac {L_{2}^{2}}{2\Theta _{2}}}+{\frac {L_{3}^{2}}{2\Theta _{3}}}+mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

Die Lagrange-Funktion kann mit den Euler-Winkeln ausgedrückt werden, deren zeitlicher Verlauf dann aus den Lagrangegleichungen resultieren.

Die Hamiltonfunktion H des Kreisels ist die Summe aus Rotationsenergie und der potentiellen Energie:

$H=E_{\rm {rot}}+E_{\rm {pot}}={\frac {L_{1}^{2}}{2\Theta _{1}}}+{\frac {L_{2}^{2}}{2\Theta _{2}}}+{\frac {L_{3}^{2}}{2\Theta _{3}}}-mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

Die Euler-Poisson Gleichungen können mit ihr und der Poisson-Klammer {} ausgedrückt werden:

${\dot {L}}_{i}=\{L_{i},H\},\quad {\dot {n}}_{i}=\{n_{i},H\}\quad {\text{für}}\;i=1,2,3$

Diese Bewegungsgleichungen lassen sich auch in der Vektorform

${\begin{aligned}{\dot {M}}=&M\times {\frac {\partial H}{\partial M}}+\gamma \times {\frac {\partial H}{\partial \gamma }}\\{\dot {\gamma }}=&\gamma \times {\frac {\partial H}{\partial M}}\end{aligned}}$

schreiben. Darin ist M der Koordinatenvektor des Drehimpulses und γ der Koordinatenvektor des Einheitsvektors in Richtung der Schwerebeschleunigung jeweils bezüglich des Hauptachsensystems.

Die Poisson Algebra e(3) dieser Variablen ist gegeben durch

$\{L_{i},L_{j}\}=-\varepsilon _{ijk}L_{k},\quad \{L_{i},n_{j}\}=-\varepsilon _{ijk}n_{k},\quad \{n_{i},n_{j}\}=0$

Darin ist ε_ijk das Levi-Civita-Symbol. Es gibt zwei Casimir Funktionen F₁ = M · γ und F₂ = γ², die bezüglich der Poisson-Klammer mit jeder Funktion von M und γ kummunizieren und die auch gleichzeitig Integrale der Hamiltonfunktion sind.

Schnell rotierender symmetrischer Kreisel

Abb. 6: Grafische Herleitung des Kreiselmoments: dL = L_⊥ dφ = sin α L dφ

Beim schnell rotierenden symmetrischen Kreisel kann im Drallsatz eine Näherung benutzt werden, die für praktische, technische Anwendungen geeignet ist. Es wird angenommen, das der rasch rotierende Kreisel durch ein Moment belastet wird, das senkrecht zu seinem Drehimpuls ist. Nach der Regel des gleichsinnigen Parallelismus ändert sich der Drehimpuls in Richtung des Moments, wobei durch die Orthogonalität von Moment und Drehimpuls, dessen Betrag (etwa) konstant bleibt. Dann überstreicht der Drehimpuls, zumindest momentan, einen Kegel mit der Kippwinkelgeschwindigkeit Ω, die in dieser Näherung deutlich kleiner sein muss als die Winkelgeschwindigkeit ω des Kreisels um seine Figurenachse, siehe Abb. 6.

Die Drehimpulsänderung $\mathrm {d} {\vec {L}}$ ergibt sich beim Kegel aus der Winkeländerung dφ und der Ausrichtung der Kippachse ${\hat {e}}_{\Omega }$ gemäß

$\mathrm {d} {\vec {L}}=\mathrm {d} \varphi \,{\hat {e}}_{\Omega }\times {\vec {L}}$

Hier trägt also nur die Komponente des Drehimpulses, die senkrecht zur Kippachse ${\hat {e}}_{\Omega }$ steht, etwas bei und der Anteil parallel zur Kippachse wird vernachlässigt. Die Winkeländerung dφ über die Zeit dt stellt des Weiteren die Kippwinkelgeschwindigkeit Ω dar. Einsetzen der Drehimpulsänderung in den Eulerschen Drehimpulssatz liefert ${\vec {M}}\mathrm {d} t=\mathrm {d} {\vec {L}}=\mathrm {d} \varphi \,{\hat {e}}_{\Omega }\times {\vec {L}}$ oder

${\vec {M}}={\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\frac {\mathrm {d} \varphi \,{\hat {e}}_{\Omega }\times {\vec {L}}}{\mathrm {d} t}}={\vec {\Omega }}\times {\vec {L}}\quad {\text{mit}}\quad {\vec {\Omega }}={\frac {\mathrm {d} \varphi }{\mathrm {d} t}}{\hat {e}}_{\Omega }$

In Komponenten mit ${\vec {M}}=M{\hat {e}}_{z},\;{\vec {L}}=L{\hat {e}}_{3}$ und ${\hat {e}}_{\Omega }\times {\hat {e}}_{3}=\sin(\alpha ){\hat {e}}_{z}$ schreibt sich das

$M=L\sin(\alpha ){\dot {\varphi }}$

Beim Spielzeugkreisel mit Drehimpuls L = B ω um seine Figurenachse ist das Moment dasjenige der Schwerkraft, M = m g s sin(α) mit dem Abstand s des Schwerpunkts vom Stützpunkt, und somit

${\dot {\varphi }}={\frac {M}{L\sin(\alpha )}}={\frac {mgs}{B\omega }}$

Lösungen der Kreiselgleichungen

Für die technische Anwendung gibt es bedeutsame Spezialfälle, bei denen sich die Kreiselgleichungen soweit vereinfachen, dass sie integrabel sind. In diesen Fällen weist die Winkelgeschwindigkeit einen periodischen Verlauf auf, können die verschiedenen Bewegungsmodi klassifiziert und die Zeitfunktionen der Variablen sowie ihre geometrische Bedeutung angegeben werden. Insbesondere beim Kowalewskaja-Kreisel und im Goryachew-Chaplygin Fall sind die analytischen Lösungen so kompliziert, dass die Herausarbeitung der vorgenannten typischen Eigenenschaften der Bewegung äußerst aufwändig ist. Hier helfen topologische Analyse (Bifurkationsdiagramm), Stabilitätsanalyse, Phasenraum-Diagramme und Computeranimationen dabei, Einblicke in die Vorgänge im Kreisel zu erhalten und deren typischen Eigenenschaften heraus zu arbeiten. Die so erzielten Ergebnisse können praktische Anwendungen motivieren.

Für eine Liouville-Integrabilität sind mindestens vier Konstanten der Bewegung erforderlich, die in den im Folgenden aufgeführten Fällen vorhanden sind. Der Euler-, Lagrange- und Kowalewskaja-Kreisel sind die einzigen Kreisel, bei denen die Gleichungen immer integrabel sind. Ansonsten könnnen die Gleichungen nur bei speziellen Bewegungen, wie im Goryachew-Chaplygin Fall, integrabel sein.

Unabhängig von anderen Einflüssen ist jeder schwere Kreisel quasi-integrabel, bei dem entweder sehr wenig oder sehr viel Energie (im Vergleich zur potentiellen Energiedifferenz zwischen unterem und oberem Totpunkt) in der Rotation steckt. Die chaotischsten Bewegungen bei den nicht integrablen Typen treten unabhängig von der Form dann auf, wenn die kinetische Energie des Kreisels gerade ausreicht, den oberen Totpunkt zu erreichen.

Euler-Kreisel

Der Fall von Euler behandelt einen Kreisel, der genau in seinem Schwerpunkt aufgehängt ist, so dass seine Gewichtskraft keine Rolle spielt. Hier sind die vier Konstanten die Drehimpulse bezüglich aller drei Raumrichtungen x, y und z des Inertialsystems und die Rotationsenergie:

${\begin{aligned}{\vec {L}}=&L_{x}{\hat {e}}_{x}+L_{y}{\hat {e}}_{y}+L_{z}{\hat {e}}_{z}\\E_{\rm {rot}}=&{\frac {1}{2}}\left({\frac {L_{1}^{2}}{\Theta _{1}}}+{\frac {L_{2}^{2}}{\Theta _{2}}}+{\frac {L_{3}^{2}}{\Theta _{3}}}\right)={\frac {1}{2}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})\end{aligned}}$

Mit der Poinsot’schen Konstruktion kann die Bewegung des Euler-Kreisels anschaulich dargestellt werden. Der eulersche Kreisel findet z. B. in Kreiselkompassen und gyroskopischen Steuersystemen technische Anwendung.

Lagrange-Kreisel

Joseph-Louis Lagrange konnte 1788 in seinem grundlegenden Werk Mécanique analytique eine weitere Lösung der Kreiselgleichungen herleiten und zwar für den symmetrischen schweren Kreisel. Dies wird von radialsymmetrischen Körpern erfüllt, die auf ihrer Symmetrieachse jedoch nicht im Schwerpunkt gelagert sind. Die Erhaltungsgrößen sind die Gesamtenergie, der Drehimpuls in Richtung des Schwerefelds und der Figurenachse sowie der Betrag des Richtungsvektors der Schwerkraft:

${\begin{aligned}E=&{\frac {1}{2}}\left({\frac {L_{1}^{2}}{A}}+{\frac {L_{2}^{2}}{A}}+{\frac {L_{3}^{2}}{C}}\right)-c_{0}n_{3}={\frac {1}{2}}(A\omega _{1}^{2}+A\omega _{2}^{2}+C\omega _{3}^{2})-c_{0}n_{3}\\L_{z}=&L_{1}n_{1}+L_{2}n_{2}+L_{3}n_{3}=A\omega _{1}n_{1}+A\omega _{2}n_{2}+C\omega _{3}n_{3}\\L_{3}=&C\omega _{3}\\1=&n_{1}^{2}+n_{2}^{2}+n_{3}^{2}\end{aligned}}$

Darin sind c₀ = m g x₀, m die Masse, g die Schwerebeschleunigung, x₀ der Abstand des Schwerpunkts vom Stützpunkt auf der Figurenachse, C = Θ₃ das Massenträgheitsmoment um die Figurenachse und A = Θ₁ = Θ₂ das Massenträgheitsmoment um dazu senkrechte Achsen. Während die ersten drei Konstanten mechanischer Natur sind, ist die letzte Konstante eine rein geometrische, die daraus folgt, dass der Schwerkraftvektor immer in dieselbe Richtung ${\vec {g}}=g{\begin{pmatrix}n_{1}&n_{2}&n_{3}\end{pmatrix}}$ weist. Diese Konstante, die Gesamtenergie und der konstante Drehimpuls in Richtung der Schwerebeschleunigung ist allen schweren Kreiseln gemeinsam, die auch in den verbleibenden beiden Fällen vorliegen.

Der Fall von Lagrange wird durch einen typischen Spielzeugkreisel realisiert, wenn dessen Aufsetzpunkt am Boden frei drehbar fixiert ist.

Kowalewskaja-Kreisel

Sofja Kowalewskaja fand 1889 den letzten integrablen Fall, der einen symmetrischen schweren Kreisel behandelt, der zwei gleiche Trägheitsmomente A bezüglich der ersten beiden Hauptachsen und ein halb so großes ½A bezüglich der dritten Hauptachse besitzt. Beim Kowalewskaja-Kreisel liegt jedoch – anders als beim Lagrange-Kreisel – der Schwerpunkt nicht auf der Figurenachse sondern senkrecht dazu. Aus Symmetriegründen kann die 1-Richtung so gewählt werden, dass der Schwerpunkt auf ihr liegt und somit ${\vec {s}}=x_{0}{\hat {e}}_{1}$ ist. Die Erhaltungsgrößen sind die Energie E, der Drehimpuls in Richtung der Schwerebeschleunigung L_z, der Betrag des Richtungsvektors der Schwerkraft und die Kowalewskaja-Konstante K, für die es keine anschauliche Interpretation gibt:

${\begin{aligned}E=&{\frac {1}{2A}}(L_{1}^{2}+L_{2}^{2}+2L_{3}^{2})-c_{0}n_{1}={\frac {A}{2}}\left(\omega _{1}^{2}+\omega _{2}^{2}+{\frac {1}{2}}\omega _{3}^{2}\right)-c_{0}n_{1}\\L_{z}=&L_{1}n_{1}+L_{2}n_{2}+L_{3}n_{3}={\frac {A}{2}}(2\omega _{1}n_{1}+2\omega _{2}n_{2}+\omega _{3}n_{3})\\K=&(L_{1}^{2}-L_{2}^{2}+2c_{0}An_{1})^{2}+4(L_{1}L_{2}+c_{0}An_{2})^{2}\\=&A^{2}(A\omega _{1}^{2}-A\omega _{2}^{2}+2c_{0}n_{1})^{2}+4A^{2}(A\omega _{1}\omega _{2}+c_{0}n_{2})^{2}\\1=&n_{1}^{2}+n_{2}^{2}+n_{3}^{2}\end{aligned}}$

Darin ist c₀ = m g x₀, m die Masse und g die Schwerebeschleunigung.

Goryachew-Chaplygin-Kreisel

Dmitri Nikanorowitsch Gorjatschew (Goryachev) fand 1900 eine spezielle Kreiselbewegung, die ebenfalls integrabel ist, und Tschaplygin (Chaplygin) konnte Goryachevs Lösung 1948 deutlich vereinfachen. Der Fall von Goryachew-Chaplygin ist eine Abwandlung des Kowalewskaja-Falles, der statt halb so großem dritten Trägheitsmoment ein ein viertel so großes fordert. In diesem Fall gibt es allerdings nur dann eine vierte Erhaltungsgröße, wenn der Drehimpuls L_z in Richtung der Schwerkraft anfänglich verschwindet. Da das Moment der Schwerkraft senkrecht zu ihrer Richtung wirkt, ist dann L_z = 0 eine Konstante der Bewegung. Ebenso bleiben die Gesamtenergie, der Betrag des Richtungsvektors der Schwerkraft und eine Chaplygin-Konstante G unverändert:

${\begin{aligned}E=&{\frac {1}{2A}}(L_{1}^{2}+L_{2}^{2}+4L_{3}^{2})-c_{0}n_{1}={\frac {A}{2}}\left(\omega _{1}^{2}+\omega _{2}^{2}+{\frac {1}{4}}\omega _{3}^{2}\right)-c_{0}n_{1}\\L_{z}=&L_{1}n_{1}+L_{2}n_{2}+L_{3}n_{3}={\frac {A}{4}}(4\omega _{1}n_{1}+4\omega _{2}n_{2}+\omega _{3}n_{3})\equiv 0\\G=&4L_{3}(L_{1}^{2}+L_{2}^{2})+4c_{0}AL_{1}n_{3}=A^{3}\omega _{3}(\omega _{1}^{2}+\omega _{2}^{2})+4A^{2}c_{0}\omega _{1}n_{3}\\1=&n_{1}^{2}+n_{2}^{2}+n_{3}^{2}\end{aligned}}$

Darin sind A das Trägheitsmoment bezüglich zweier Hauptachsen, ¼A das dritte Hauptträgheitsmoment, c₀ = m g x₀, m die Masse, g die Schwerebeschleunigung und x₀ der Abstand des Schwerpunkts vom Stützpunkt in 1-Richtung.

Siehe auch

Gyroskopischer Effekt