Würfelverdoppelung

Die Würfelverdoppelung, auch bekannt als Delisches Problem, bezeichnet die geometrische Aufgabe, zu einem gegebenen Würfel einen zweiten Würfel mit dem doppelten Volumen zu konstruieren. Das Problem gehört zu den drei „klassischen Problemen der antiken Mathematik“ und wurde bereits im 5. Jahrhundert v. Chr. im antiken Griechenland formuliert.
Ein Ausgangswürfel mit der Kantenlänge (ein sogenannter Einheitswürfel) hat das Volumen Ein weiterer Würfel habe die Kantenlänge und das Volumen Die neue Kantenlänge ist die Kubikwurzel aus , also . Diese kann als Grenzwert geeigneter Folgen bestimmt werden, ist jedoch aus den Strecken 0 und 1 über Zirkel und Lineal nicht in endlich vielen Schritten konstruierbar. Versucht man also das Problem der Würfelverdoppelung ausschließlich mit den Hilfsmitteln zu bearbeiten, die Euklid in seinen Elementen nutzte, nämlich mit Zirkel und unmarkiertem Lineal, ist es nicht lösbar. Diese Aussage lässt sich in die Sprache der Algebra übersetzen, wodurch schließlich ein mathematischer Beweis für die Unmöglichkeit der Konstruktion angegeben werden kann. Ein solcher wurde zuerst vom französischen Mathematiker Pierre Wantzel im Jahr 1837 veröffentlicht. Jedoch gilt es als sehr wahrscheinlich, dass Carl Friedrich Gauß bereits früher einen Beweis kannte, diesen aber nicht niederschrieb.
Analoge Probleme bestehen bei Vergrößerungen des Würfelvolumens auf das 3-, 4-, 5-, 6- und 7-fache des ursprünglichen Rauminhaltes. Dagegen ist die Aufgabe zum Beispiel einer Volumenverachtfachung kein Problem, weil die Kubikwurzel aus 8 problemlos berechenbar und die resultierende Kantenlängenverdoppelung leicht machbar ist.
Schwächt man die Einschränkung ab und lässt ein zusätzliches Hilfsmittel zu, wie zum Beispiel entsprechende Markierungen auf dem Lineal oder spezielle Kurven, dann ist die Konstruktion eines Würfels mit doppeltem Volumen möglich. Entsprechende Verfahren waren bereits in der Antike bekannt.
Geschichtliches aus der Antike
[Bearbeiten | Quelltext bearbeiten]
Die wichtigste antike Quelle zur Würfelverdoppelung ist der Kommentar des spätantiken Autors Eutokios zu Archimedes’ Schrift „Über Kugel und Zylinder“ („Περὶ σφαίρας καὶ κυλίνδρου Peri sphairas kai kylindrou“), in dem diverse Lösungsansätze antiker Mathematiker gesammelt sind.[1] Unter anderem wird dort ein Brief des Gelehrten Eratosthenes (um 275–194 v. Chr.) an einen König Ptolemaios (wohl Ptolemaios III. oder Ptolemaios IV.) wörtlich zitiert, der mittlerweile als authentische Wiedergabe des Originalbriefes erwiesen wurde und in dem der Wissenschaftler sich dem Herrscher gegenüber zur Frage der Würfelverdopplung äußert.[2] Als ältesten Beleg für dieses mathematische Problem zitiert Eratosthenes dort „einen der alten Tragödiendichter“ („τῶν ἀρχαίων τινὰ τραγῳδοποιῶν tōn archaiōn tina tragōdopoiōn“), in dessen Werk der mythische König Minos das Grab seines Sohnes Glaukos errichten lässt und den Baumeister anweist, es doppelt so groß wie den ersten Entwurf anzufertigen, aber die Würfelform beizubehalten.[3] Von den drei bedeutenden athenischen Tragödiendichtern des 5. Jahrhunderts v. Chr. – Aischylos, Sophokles und Euripides – weiß man, dass sie in je einem ihrer Werke die Sage von Minos und Glaukos aufgriffen; dennoch ist möglich, dass das Zitat aus einer Tragödie eines ganz anderen Dichters stammt.[4]
Die Alternativbezeichnung „Delisches Problem“ geht auf eine Episode zurück, die Eratosthenes in seinem Brief ebenfalls anführt,[3] die aber auch bei diversen anderen antiken Autoren (darunter Plutarch und Theon von Smyrna) beschrieben wird und der aus altertumswissenschaftlicher Sicht durchaus ein tatsächliches historisches Ereignis zugrunde liegen könnte: Die Bewohner der Insel Delos hätten während einer schweren Seuche ein Orakel um Rat gefragt, was sie tun könnten, um ihre Situation zu verbessern. Das Orakel habe sie angewiesen, den würfelförmigen Altar im Apollontempel der Insel in seiner Größe – also seinem Volumen – zu verdoppeln. Die delischen Architekten seien jedoch ratlos gewesen, wie das konkret zu bewerkstelligen wäre, und hätten daraufhin Platon (428/427–348/347 v. Chr.) um Rat gebeten.[3] Dieser habe sie an Archytas von Tarent, Eudoxos von Knidos und Menaichmos verwiesen, die ihnen jeweils unterschiedliche Lösungsansätze eröffnet hätten. Laut Plutarch habe Platon deren Ansätze jedoch kritisiert, da sie ihm zufolge durch die Nutzung mechanischer Methoden das „Gute“, Elegante der Geometrie zerstören.[5] Im Archimedes-Kommentar des Eutokios wird Platon interessanterweise auch eine eigene mechanische Lösung des Delischen Problems (siehe Abschnitt Platons mechanische Methode) zugeschrieben. Sofern damit nicht ein anderer Platon gemeint ist als der berühmte Philosoph, dürfte es sich dabei nach vorherrschender Forschungsmeinung jedoch um eine Falschzuschreibung handeln.[6]
Ähnliche Probleme aus der Konstruktion von Altären (allerdings mit dem Problem der Verdopplung eines Quadrats statt eines Würfels) gab es in vedischer Zeit in Indien und sie gaben zu mathematischen Erörterungen Anlass (Sulbasutras).[7] Beim Quadrat lässt sich die Aufgabe der Verdopplung durch den Satz des Pythagoras lösen.
Antike Lösungen mit zusätzlichen Hilfsmitteln
[Bearbeiten | Quelltext bearbeiten]- Hippokrates von Chios (zweite Hälfte des 5. Jahrhunderts v. Chr.) zeigte als Erster den maßgeblichen Ansatz für eine theoretische Lösung des Problems. Er fand: Das Problem der Würfelverdoppelung ist äquivalent zu demjenigen der Bestimmung von zwei mittleren Proportionalen zweier Größen.[8] Dies bedeutet, dass für eine Strecke nach zwei Strecken und gesucht wird, so dass
- Dies zieht nach sich.
- Archytas von Tarent (435/410–355/350 v. Chr.) war der Erste, dem die Umsetzung des oben genannten Satzes von Hippokrates unter Zuhilfenahme der nach ihm benannten Kurve gelang; beschrieben im Abschnitt Kurve des Archytas.[9]
- Platon (428/427–348/347 v. Chr.) wurde von Eutokios als Erster benannt, der zur Lösung der Würfelverdoppelung eine mechanische Methode fand.[10] Wie bereits oben erwähnt, dürfte diese Lösung nicht von ihm stammen.
- Eudoxos (397/390–345/338 v. Chr.) fand eine Lösung – so wird berichtet – durch die Konstruktion der zwei mittleren Proportionalen mithilfe nicht näher bekannter Kurven und ihrer Schnittpunkte.[11]
- Menaichmos (um 380–320 v. Chr.) fand zwei Lösungen: eine, in der eine Parabel von einer Hyperbel geschnitten wird, und eine zweite, ausführlich beschrieben im Abschnitt Parabel nach Menaichmos, als Schnitt zweier Parabeln.[12]
- Eratosthenes (um 278–194 v. Chr.) beschreibt in seinem Brief an König Ptolemaios im Anschluss an seine Einführung zur Geschichte des Delischen Problems eine eigene „mechanische Methode“[13] durch einen Apparat, den er „Mesolabium“ nannte.[14]
- Diokles (um 240–180 v. Chr.) benutzte für seine Lösung eine nach ihm benannte Zissoide; beschrieben im Abschnitt Zissoide des Diokles.[15]
- Sporus (* um 240–um 300) wie auch Pappos erschufen eine Konstruktion, die nahezu gleich der von Dürer ist, beschrieben im Abschnitt Albrecht Dürers Konstruktion mithilfe eines Lineals mit Strichskale.
Beweis der Unlösbarkeit mittels Zirkel und Lineal
[Bearbeiten | Quelltext bearbeiten]Geschichte des Beweises
[Bearbeiten | Quelltext bearbeiten]Grundsätzlich griffen die Mathematiker der Antike bei der Lösung von Problemen nicht nur auf Zirkel und Lineal zurück. Die Vermutung, dass es eine solche methodische Beschränkung gegeben habe, erwies sich als neuzeitlicher Mythos.[16] Dass die Aufgabe bei alleiniger Verwendung von Zirkel und Lineal auch tatsächlich unlösbar ist, bewies Pierre Wantzel im Jahr 1837.[17][18] Sein Beweis beruhte auf folgenden algebraischen Überlegungen:[19]
- 1. Im ersten Teil des Beweises argumentiert er, dass, wenn ein Konstruktionsproblem mit Lineal und Zirkel gelöst werden kann, „die Unbekannte des Problems durch die Lösung einer Reihe von quadratischen Gleichungen erhalten werden kann, deren Koeffizienten rationale Funktionen der Parameter des Problems und der Wurzeln der vorherigen Gleichungen sind“.
Mit der „Unbekannten des Problems“ ist dabei z. B. die gesuchte Strecke gemeint.
- 2. Danach zeigte er, dass jede algebraische Zahl , die Lösung der letzten Gleichung eines Systems
- ist, wobei die Koeffizienten stets durch sukzessive Adjunktion im Körper liegen, stets von einem Polynom des Grades mit Koeffizienten in gelöst wird. Dabei löst die Gleichung und sind die gegebenen Parameter des Problems.
- 3. Wantzel wusste, dass jede algebraische Zahl Lösung eines Polynoms mit Grad einer Zweierpotenz ist, wenn diese hinreichend groß gewählt würde. Daher war sein Hauptresultat, zu zeigen, dass, wenn die Anzahl an benötigten Gleichungen zu einem Minimum reduziert würde, das resultierende Polynom irreduzibel über ist.
Die Unmöglichkeit der Konstruktion folgt nun als Korollar aus den Sätzen 1 bis 3: Wäre, beginnend beim Einheitswürfel, die Konstruktion der Würfelverdoppelung mit Zirkel und Lineal möglich, so müsste Nullstelle eines irreduziblen Polynoms über sein, das als Grad eine Zweierpotenz hat. Das Polynom ist irreduzibel über , hat aber den Grad 3. Dies ist ein Widerspruch.
Es ist zu beachten, dass Wantzels Originalpublikation von dem Mathematikhistoriker Jesper Lützen als lückenhaft und schwer zu verstehen angesehen wird – dies betrifft vor allen Dingen den „Beweis“ des Hauptsatzes 3. Von Lützen wurden die Lücken im Nachhinein geschlossen und die Resultate, wie oben beschrieben, in moderner Fachsprache formuliert.[20] Wantzels Beweis für die Unmöglichkeit, die Verdoppelung des Würfels und die Dreiteilung des Winkels mit Lineal und Zirkel zu konstruieren, war nach seiner Veröffentlichung im Jahr 1837 fast ein Jahrhundert lang vergessen. Laut Lützen waren dabei die „mangelnde Berühmtheit des Autors“, die „Tatsache, dass einige seiner Zeitgenossen das Ergebnis als bekannt oder sogar als bewiesen ansahen“, und dass „das Ergebnis zum Zeitpunkt seiner Veröffentlichung nicht als wichtiges mathematisches Ergebnis angesehen wurde“, die treibenden Gründe.[21]

Es wird von Historikern bezweifelt, dass Wantzel als Erster um einen Beweis wusste, da der junge Carl Friedrich Gauß sehr wahrscheinlich über einen solchen verfügt hat.[22] Ein großer Teil seines 1801 erschienenen Werkes Disquisitiones arithmeticae ist der Frage gewidmet, welche Bedingungen eine Polynomgleichung erfüllen muss, um durch quadratische Radikale lösbar zu sein. Dort finden sich auch die nach Gauß benannten Sätze, mit deren Hilfe für die meisten klassischen Aufgaben die Unlösbarkeit mit Zirkel und Lineal nachgewiesen werden kann. Mit seinen entwickelten Techniken bewies Gauß zum Beispiel, dass sich das 17-Eck mit Zirkel und Lineal konstruieren lässt. Die Tatsache, dass trotzdem Wantzel von vielen Autoren als Urheber der Sätze genannt und zitiert wird, führen die Mathematikhistoriker Christoph Scriba und Peter Schreiber auf die „Kommunikationsschwierigkeiten“ der Wissenschaft des 19. Jahrhunderts zurück.[23]
In heutiger Fachsprache ist der Beweis eine Anwendung der umfassenden Galoistheorie (nach Évariste Galois, französischer Mathematiker) und läuft im Kern darauf hinaus, dass die irrationale Zahl nicht durch ganze Zahlen, nicht durch die vier Grundrechenarten und auch nicht durch Quadratwurzeln ausgedrückt werden kann.
Algebraischer Beweis
[Bearbeiten | Quelltext bearbeiten]
Diese Zahl kann nicht aus ganzen Zahlen über Verkettungen aus Grundrechenoperationen wie Plus, Mal, Geteilt oder Quadratwurzeln gewonnen werden. Letztere sind aber genau die Zahlen, die bei den Strecken und beginnend mittels Zirkel und Lineal konstruiert werden können.
Im Detail kann der Beweis der Unmöglichkeit über folgende Ideen aus der Algebra vollzogen werden. Es seien eine Menge von Punkten (komplexen Zahlen), welche mindestens 0 und 1 enthält, und ein beliebiger Punkt gegeben. Es ist für diese Überlegungen von Wichtigkeit, dass die komplexen Zahlen als Ebene aufgefasst werden können – im Gegensatz dazu werden die reellen Zahlen schlicht als Gerade aufgefasst. Dann gilt, dass der Punkt genau dann mit Zirkel und Lineal aus den Punkten konstruierbar ist, falls er in einem Körper (dabei ist der Körper der komplexen Zahlen) liegt, der durch Adjunktion einer Quadratwurzel aus dem Körper
hervorgeht. Dabei ist grob gesprochen die Menge, die aus Bilden aller Summen, Produkte und Quotienten aus rationalen Zahlen mit entsteht. Hier ist die Menge der komplex Konjugierten von und das Symbol steht für die Vereinigung zweier Mengen. Adjunktion einer Quadratwurzel bedeutet, dass es ein geben muss, so dass . Zum Beispiel geht durch die Adjunktion einer Quadratwurzel aus den rationalen Zahlen hervor, da eine rationale Zahl ist – entsprechend ist die Menge aller Summen, Produkte und Quotienten rationaler Zahlen mit der Zahl . Bei handelt es sich um eine sogenannte Körpererweiterung. Das Problem der Würfelverdopplung mittels Zirkel und Lineal lässt sich also auf die Frage reduzieren, ob die Zahl in einem Teilkörper von liegt, der aus durch sukzessive Adjunktion von Quadratwurzeln gewonnen werden kann. Das bedeutet jedoch, dass der Erweiterungsgrad von aus eine Potenz von 2 sein muss. Es ist aber
womit es unmöglich ist, die Würfelverdopplung mittels Zirkel und Lineal vorzunehmen.[24] Dass die Körpererweiterung vom Grad 3 ist, kann wie folgt gesehen werden: Das Polynom ist irreduzibel über den ganzen Zahlen und hat als höchsten Koeffizienten 1. Nach dem Lemma von Gauß ist dann bereits irreduzibel über den rationalen Zahlen. Damit ist bereits das Minimalpolynom von und dieses hat den Grad 3. Daraus ergibt sich die Erkenntnis, dass jedes Element der Menge , bestehend aus allen rationalen Zahlen, die mit der Kubikwurzel aus 2 beliebig durch die Grundrechenarten „vermengt“ wurden, eindeutig als mit rationalen Zahlen geschrieben werden kann. Zum Beispiel ist
Damit wird zu einem drei-dimensionalen Vektorraum über .
Mit dem gleichen Argument lässt sich zeigen, dass auch eine Würfelvervielfachung um einen natürlichen Faktor , der keine Kubikzahl ist, sich nicht mit Zirkel und Lineal bewerkstelligen lässt.
Geometrische Konstruktionen mit mechanischen Hilfsmitteln
[Bearbeiten | Quelltext bearbeiten]Nimmt man zu den klassischen (euklidischen) Werkzeugen Zirkel und unmarkiertes Lineal ein weiteres mechanisches Hilfsmittel, wie zum Beispiel ein spezielles mechanisches Werkzeug[25] oder ein entsprechend markiertes Lineal, so kann die zur Würfelverdoppelung erforderliche Kantenlänge des Würfels theoretisch exakt dargestellt werden.
Mithilfe eines markierten Lineals
[Bearbeiten | Quelltext bearbeiten]Konstruktionen mithilfe einer sogenannten Einschiebung,[26] auch als Neusis-Konstruktionen bezeichnet, verwenden neben dem Zirkel auch ein Lineal, auf dem eine spezielle Markierung als zusätzliche Hilfe aufgebracht ist.
Die folgende Neusis-Konstruktion in Bild 1, Heinrich Dörrie nennt sie Papierstreifenkonstruktion,[27] ist eine der bekanntesten. Sie stammt ursprünglich von Isaac Newton aus seinem in Latein erschaffenen Werk Arithmetica Universalis.
Konstruktion 1
[Bearbeiten | Quelltext bearbeiten]- Bezeichnet man die Kante des Ausgangswürfels mit , wird damit zunächst ein gleichseitiges Dreieck mit den Ecken konstruiert. Es folgt die Verdoppelung der Strecke ab dabei ergibt sich der Schnittpunkt Nun wird die Strecke ab verlängert. Anschließend wird eine Halbgerade ab durch gezeichnet. Nun setze ein mit dem Punkt markiertes Lineal (Abstand Ecke bis Punkt entspricht ) so auf die Zeichnung, dass dessen Ecke auf der Verlängerung der Strecke anliegt, die Markierung Punkt auf der Verlängerung der Strecke aufliegt und die Kante des Lineals durch den Punkt verläuft. Abschließend verbinde den Punkt mit
- Die Strecke ist die Kantenlänge des gesuchten Würfels mit dem verdoppelten Volumen des Ausgangswürfels.
Die Darstellung im Bild 2 sowie die folgende sinnmäßig übersetzte Beschreibung dazu, sind nach Isaac Newton.
- Ich ziehe eine beliebige Linie, K A = a, halbiere sie in C und ziehe um den Mittelpunkt K mit Abstand K C einen Kreisbogen, ich bestimme C X = b und ziehe eine gerade Linie durch A X und eine durch C X, ich markiere E Y = C A, sodass eine gerade Linie durch E Y sowie durch den Punkt K gehen kann. [...][28]

und sind die mittleren Proportionalen von und , wobei die Kante des Ausgangswürfels ist.

Konstruktion 2
[Bearbeiten | Quelltext bearbeiten]Von Isaac Newton stammt auch diese weniger bekannte Neusis-Konstruktion (Bild 3),[29] die aber wegen ihrer Einfachheit bemerkenswert ist.

Kante des Ausgangswürfels,
.
- Sie beginnt mit dem Errichten einer Senkrechten , gleich der Kante des Ausgangswürfels, auf eine Halbgerade ab . Ein Winkelschenkel mit der Winkelweite am Scheitel schließt sich an. Nun setze ein mit dem Punkt markiertes Lineal (Abstand Ecke bis Punkt entspricht ) so auf die Zeichnung, dass dessen Ecke auf dem Winkelschenkel liegt, die Markierung Punkt auf der Halbgeraden ab aufliegt und die Kante des Lineals durch den Punkt verläuft. Abschließend verbinde den Punkt mit Der eingezeichnete Punkt dient nur der einfacheren Formulierbarkeit im folgenden Beweis.
- Die Strecke ist die Kantenlänge des gesuchten Würfels mit dem verdoppelten Volumen des Ausgangswürfels.
Beweis der Richtigkeit
[Bearbeiten | Quelltext bearbeiten]- Das Bild 3 zeigt, die rechtwinkligen Dreiecke (blau) und (grün) sind wegen des Scheitelwinkels zueinander ähnlich,
- folglich gilt nach dem 2. Strahlensatz
- (1)
- rechtwinkliges Dreieck und Tangens
- (2)
- Teile der Gleichung (2) quadriert
- (3)
- umgeformt ergibt sich
- (4)
- rechtwinkliges Dreieck nach Satz des Pythagoras
- (5)
- Wert von (5) eingesetzt in (4)
- (6)
- (6)
- umgeformt ergibt sich
- (7)
- nach der Vereinfachung
- (8)
- folgt daraus schließlich
- (9)
- In Worten:
- Das Volumen des Würfels mit der Kantenlänge ist gleich dem doppelten Volumen des Ausgangswürfels mit der Kantenlänge
Albrecht Dürers Konstruktion mithilfe eines Lineals mit Strichskale
[Bearbeiten | Quelltext bearbeiten]Albrecht Dürer veröffentlichte 1525 in seinem Werk Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen, neben einer Näherungskonstruktion zur Dreiteilung des Winkels auch eine theoretisch exakte Lösung zur Würfelverdoppelung.[30] Als zusätzliches Hilfsmittel verwendete er dafür ein Lineal mit aufgezeichneter Strichskale.

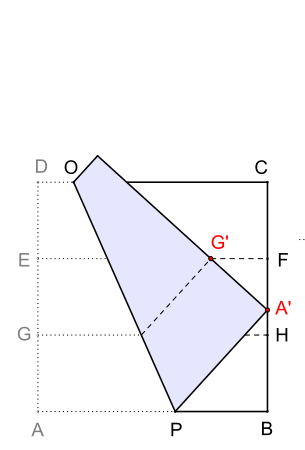
Bereits im 3. Jahrhundert n. Chr. löste Sporus von Nikaia dieses antike Problem anhand einer Konstruktion, die nahezu gleich der von Pappos und der von Dürer ist. Alle drei Lösungen benötigen eine sogenannte Neusis-Konstruktion. Im Gegensatz zu Dürer geben Sporus sowie Pappos keine näheren Hinweise bezüglich einer Markierung auf dem Lineal, mit dessen Hilfe (Linealkante verläuft durch die Punkte und ) die Gleichheit [31] gefunden werden kann.[32]
In der nebenstehenden Darstellung ist die Kantenlänge des Ausgangswürfels sowie das – in einer externen Konstruktion bestimmte – geometrische Mittel von und . Sporus zeigt als Lösung die Verhältnisgleichung
- es gilt auch [32]
Sei , dann ist , und . Eingesetzt in die Verhältnisgleichung
ergibt jeder dieser Quotienten den Wert für die Kantenlänge des verdoppelten Würfels.
Die in der Darstellung gepunkteten Linien sowie die Punkte und sind nicht Teil der Konstruktion, sie dienen lediglich der Beweisführung.[33]
Grundkonstruktion nach Dürer
[Bearbeiten | Quelltext bearbeiten]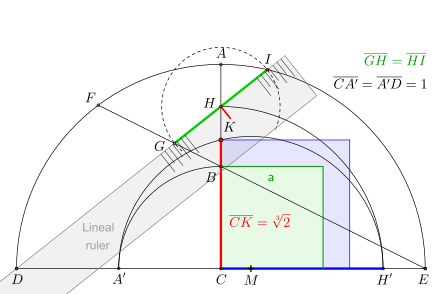
Zunächst stellt man sich zwei exakt aufeinanderliegende Würfel mit gleicher Kantenlänge vor, z. B. mit . Auf ihrer gemeinsamen Mittelachse bestimmen sie somit die Punkte und . Der anschließende Halbkreis mit dem Radius um erzeugt den Durchmesser , der mit der Mittelachse einen rechten Winkel bildet. Die nächste Linie wird ab Punkt durch gezogen, bis sie den Halbkreis in schneidet. Die Grundkonstruktion ist somit fertiggestellt.
Nun ist die Aufgabe gestellt, mithilfe eines Lineals die Punkte und so zu bestimmen, dass die Strecken und die gleiche Länge aufweisen.
Ermittlung der gleichen Strecken GH und HI
[Bearbeiten | Quelltext bearbeiten]
Ermittlung der Strecken mit zwei möglichen Vorgehensweisen, dazwischen und am Ende jeweils 15 s Pause
- Dafür nimmt man ein schmales Lineal und bringt an einer Kante eine Strichskale mit gekennzeichneter Mitte an. Nun dreht und schiebt man das Lineal Schritt für Schritt vom Punkt in Richtung Punkt , dabei verläuft die Kante des Lineals stets durch den Punkt und die Skalenmitte (roter Strich) bewegt sich auf der Mittelachse . Das Ziel ist erreicht, wenn beide Punkte und den gleichen Abstand zur Skalenmitte haben.
- Denkbar ist hierfür auch eine Vorgehensweise, bei der man ein unmarkiertes Lineal und einen Zirkel verwendet. Hierzu dreht man das Lineal wieder Schritt für Schritt vom Punkt in Richtung Punkt , dabei verläuft die Kante des Lineals stets durch den Punkt . Nach jedem dieser Schritte werden die Schnittpunkte und markiert und danach ein Kontrollkreisbogen (strichlierte Linie) mit dem Radius um eingetragen. Das Ziel ist erreicht, wenn beide Punkte und auf dem Kontrollkreisbogen liegen.
Fertigstellung der Konstruktion
[Bearbeiten | Quelltext bearbeiten]Weiter geht es mit dem Ziehen des Viertelkreises um mit Radius , bis er die Strecke in schneidet, sowie des weiteren Viertelkreises um mit Radius , bis er die Strecke in schneidet. Es folgt die Halbierung der Strecke in . Schließlich liefert der Halbkreis um über , mit Schnittpunkt auf dem Radius , die theoretisch exakte Kantenlänge des verdoppelten Würfels.
Wegen ergibt sich darüber hinaus: Die Kantenlänge ist auch die Quadratwurzel der Länge (siehe Quadratwurzel, Konstruktion mit Zirkel und Lineal).
Beweis der Richtigkeit
[Bearbeiten | Quelltext bearbeiten]Wird angenommen, dass die Strecke wahr ist (siehe Berechnungsskizze), dann ist ein möglicher Beweis für = , wenn die Behauptung = wahr ist.

Verwendet werden hierzu die vier rechtwinkligen und – wegen ihrer gleichen Innenwinkel – zueinander ähnlichen Dreiecke , , und
- Rechtwinkliges Dreieck , darin ist und .
- Nach dem Satz des Pythagoras gilt:
- (1) .
- Rechtwinkliges Dreieck , wegen Ähnlichkeit der Dreiecke gilt nach dem W:W:W-Satz
- (2) , sowie
- (3) .
- Rechtwinkliges Dreieck , darin ist , wegen gilt
- (4)
- Rechtwinkliges Dreieck , wegen gilt
- (5) ,
- wegen gilt
- (6) .
- Nun bedarf es nur noch zweier Differenzen von Strecken
- (7) .
- (8)
- Daraus folgt
- (9) .
- Somit ist , was zu beweisen war.
Ermittlung der zwei mittleren Proportionalen mithilfe eines mechanischen Werkzeugs
[Bearbeiten | Quelltext bearbeiten]Die Verwendung der beiden im Folgenden beschriebenen mechanischen Werkzeuge liefert die sogenannten zwei mittleren Proportionalen und des Hippokrates von Chios.[34] Sie werden für die Verdoppelung des Ausgangswürfels mit der Kantenlänge benötigt. Die mittlere Proportionale entspricht der gesuchten Kantenlänge des verdoppelten Würfels.
- Der Satz des Hippokrates von Chios ist im Abschnitt Konstruktion über spezielle Kurven beschrieben.
Platons mechanische Methode
[Bearbeiten | Quelltext bearbeiten]
= Kantenlänge des Ausgangswürfels, und = Kantenlänge des verdoppelten Würfels, Animation am Ende 25 s Pause.
Wie in der Einleitung erwähnt, benennt Eutokios Platon als den Ersten, der die folgende Methode zur Lösung des Problems der Würfelverdoppelung anwandte. Zwar sprechen neuzeitliche Kommentatoren Platon dies wegen seiner vehementen Ablehnung mechanischer Hilfsmittel ab,[35] aber Lattmann beschreibt in seiner Studie Mathematische Modellierung bei Platon zwischen Thales und Euklid aus dem Jahr 2019 ausführlich, warum die Lösung zu Recht Platon zugeschrieben werden kann.[36]
„Konträr zur communis opinio steht fest, dass die Anekdote vom Delischen Problem weder insgesamt noch partiell fiktiv ist, sondern mit aller Wahrscheinlichkeit historisch korrekt ist. Auf dieser Grundlage kann in einem zweiten Schritt der in der Überlieferung Platon zugeschriebene Ansatz zum Delischen Problem als potentiell genuines, wenn auch indirekt überliefertes Platon-Zeugnis in den Blick genommen werden.“
Das mechanische Werkzeug (ohne eine Werkstoffangabe) besteht z. B. aus zwei U-förmigen Linealen. Damit das lose Lineal exakt parallel zu seinem Gegenüber verschiebbar ist, wird es in den beiden Seitenteilen entsprechend geführt.[25] Für eine gute Übersichtlichkeit ist das Werkzeug in der Draufsicht dargestellt. In der nebenstehenden Zeichnung wurden die originären teilweise griechischen Punktebezeichnungen verwendet.
Vorgehensweise
[Bearbeiten | Quelltext bearbeiten]Zuerst werden die beiden gegebenen Variablen und senkrecht zueinander und mit Verlängerungen ab dem Punkt gezeichnet.
Das Werkzeug wird nun auf folgende Art und Weise auf der Zeichnung bewegt (siehe Animation), bis die zwei mittleren Proportionalen und gefunden sind:
Die Innenkante des Grundelements verläuft stets durch Punkt und der Punkt liegt stets auf der Verlängerung der Strecke bevor der Punkt des Lineals auf die Verlängerung der Strecke geschoben wird.
Als Ergebnis liefert das mechanische Werkzeug
- und
Nachweis
[Bearbeiten | Quelltext bearbeiten]
Wegen der Parallelität und vier rechter Winkel am Scheitel haben die folgenden Dreiecke gleiche Winkel und sind daher zueinander ähnlich:[35]
Da der Scheitel einen rechten Winkel hat, sind folgende Winkel gleich:
Euklid, Elemente, 1, 32:[39]
Weil der Scheitel einen rechten Winkel hat, sind auch folgende Winkel gleich:
Nach Euklid, Elemente 6, 4 ergeben sich somit die Proportionen:[40]
Eratosthenes’ mechanische Methode
[Bearbeiten | Quelltext bearbeiten]Eratosthenes von Kyrene ersann (basierend auf dem Satz des Hippokrates) ein mechanisches Werkzeug, das er in dem Brief an König Ptolemaios beschrieb als eine:
„[…] mechanische Vorrichtung zur Bestimmung, mittels deren wir zwischen zwei gegebenen geraden Linien nicht nur zwei mittlere Proportionale finden werden, sondern soviele man zu finden anordnet.“[41]
Die mechanische Vorrichtung ist vorstellbar als ein Kasten, gefertigt aus Holz, Bronze oder Elfenbein, mit drei sehr dünnen Täfelchen in Form identischer rechtwinkliger Dreiecke, die mithilfe von Rillen nach rechts oder links verschoben werden können. Bei einer Aufgabe, in der zu zwei Variablen mehr als zwei mittlere Proportionale gesucht sind, ist die erforderliche Anzahl der Dreiecke stets um eins größer als die Anzahl der gesuchten mittleren Proportionalen.[42] Eratosthenes ließ seine Lösung der Würfelverdoppelung im Tempel der Ptolemäer in Alexandria in Stein meißeln.[43]

= Kantenlänge des Ausgangswürfels, und = Kantenlänge des verdoppelten Würfels,
Animation am Ende 10 s Pause.
Die im nebenstehenden Diagramm abstrahiert dargestellte mechanische Vorrichtung – wie Eratosthenes sie nennt – zeigt zwei parallele Strahlen und sie symbolisieren zwei Lineale. Zwischen den Linealen sind drei rechtwinklige Dreiecke, das erste ist fest am Punkt die beiden anderen sind bis verschiebbar geführt. Alternativ sind auch drei Rechtecke mit eingezeichneten Diagonalen möglich. Die hochkant gezeichneten Dreiecke haben als Höhe die Variable und eine kleine Kathete mit frei wählbarer Länge (im Diagramm ). Auf der zu senkrecht stehenden Strecke , im Punkt des dritten Dreiecks, ist die Länge der zweiten Variablen als Strecke abgetragen.[44] Ein (nicht eingezeichneter) Strahl ab Punkt durch schneidet in die Linie , erzeugt die Strecke und lässt somit die Grundidee der Vorrichtung, nämlich den Strahlensatz, erkennen.
Vorgehensweise
[Bearbeiten | Quelltext bearbeiten]Nur wenige Schritte sind erforderlich, wenn z. B. das zweite Dreieck (blau) und das dritte Dreieck (gelb) auf folgende Art und Weise zwischen den Linealen bewegt werden, bis die zwei mittleren Proportionalen und gefunden sind (siehe Animation):
Stets zuerst das zweite Dreieck (blau) so in Richtung Punkt verschieben, dass sich dessen Hypotenuse , die Strecke (rot) und die Senkrechte im Punkt schneiden. Erst im nächsten Schritt das dritte Dreieck (gelb) so nachschieben, dass sich dessen Hypotenuse , die Strecke (rot) und die Senkrechte im Punkt schneiden. Wiederholungen dieser Schritte liefern die zwei mittleren Proportionalen und
Nachweis
[Bearbeiten | Quelltext bearbeiten]Wenn sich die beiden Strahlen durch bzw. durch in schneiden, dann ist

und
- ,
während
deshalb
Ähnlich
Damit sind und in kontinuierlicher Proportion sowie und die zwei mittleren Proportionalen.
Konstruktion mittels spezieller Kurven
[Bearbeiten | Quelltext bearbeiten]
Soll ein Würfel mit der Kantenlänge bezüglich seines Volumens mit als Kantenlänge des größeren Würfels verdoppelt werden, so gilt zur Bestimmung der zwei mittleren Proportionalen und der Satz des Hippokrates von Chios:[34]
Eliminiert man , so ergibt sich:
daraus folgt:[34]
- (1)
Eliminiert man , so ergibt sich:
daraus folgt:
- (2)
Aus Gründen des besonderen Schwierigkeitsgrades – Dreidimensionalität, erste Hälfte des 4. Jahrhunderts v. Chr. – wird im Folgenden die Lösung des Problems mithilfe der Kurve des Archytas ausführlich beschrieben.
Kurve des Archytas
[Bearbeiten | Quelltext bearbeiten]
Gekennzeichnet ist dies durch den Kreuzungspunkt (grün) der beiden Durchdringungskurven, die durch das Zusammenspiel der drei Figuren entstehen: Halbzylinder mit Kurve des Archytas (rot gepunktet), Achtel eines Horntorus (anthrazit) und Kegelausschnitt (gelb) mit Kegelhöhe und dreieckiger Schnittfläche (blau).
Ein paar Jahrzehnte früher als Archytas gelang Hippokrates von Chios die Verdoppelung des Würfels, indem er sie auf ein Problem der Konstruktion von Verhältnissen zurückführte.[9] Archytas von Tarent gelang deren theoretische Konstruktion mit einer nach ihm benannten speziellen Kurve. Für deren Visualisierung bzw. Anwendung bedarf es folgender drei Figuren[45] (siehe nebenstehendes Diagramm):
- Halbzylinder, steht auf einem Halbkreis mit Radius und Durchmesser Die Höhe des Halbzylinders beträgt ca.
- Achtel eines sogenannten Horntorus[46], quasi ein Torus ohne „Loch“ mit Radius .
- Kegelausschnitt , entnommen vom Kegel mit Radius und Höhe , mit dem Dreieck als dessen Schnittfläche. Der Kegelausschnitt erreicht seine maximale Größe, nämlich ein Viertel des Gesamtkegels, wenn das Dreieck mit dem Dreieck einen Winkel von einschließt und damit auf der rechteckigen Fläche des Halbzylinders liegt.
Die Kurve des Archytas ist eine sogenannte Schnittkurve, die entsteht, wenn ein Halbzylinder ein Achtel eines Horntorus durchdringt. Wie im Diagramm erkennbar, durchdringt das Viertel des Kegels die beiden benachbarten Figuren und erzeugt dadurch eine, mit der Kurve des Archytas kreuzende, zweite Schnittkurve.
Die zwei mittleren Proportionalen sind dann gefunden, wenn die Hypotenuse der dreieckigen (blauen) Schnittfläche des Kegels die Kurve des Archytas im (grünen) Punkt schneidet. Der Punkt liegt auf der Mantelfläche des Halbzylinders (auf der Kurve des Archytas), auf der dreieckigen Schnittfläche des Kegelausschnitts und auf der halbkreisförmigen Schnittfläche des Horntorus.
Geometrische Vorüberlegung
[Bearbeiten | Quelltext bearbeiten]
Das nebenstehende Bild sowie das dazu ähnliche Bild im folgenden Abschnitt zeigen den geometrischen Ansatz, den Archytas nutzte, um damit die von ihm gefundene Kurve mithilfe von zwei mittleren Proportionalen zu beschreiben.[47] Die Figur besteht u. a. aus zwei rechtwinkligen, zueinander ähnlichen Dreiecken und mit je einem Thaleskreis. Der zur Grundfläche des Halbzylinders senkrecht stehende und um Punkt drehbare Halbkreis – mit den zwei mittleren Proportionalen und – hat den Durchmesser der Durchmesser des Halbzylinders (s. Bild Kurve des Archytas) ist
Mit eingesetzten Werten aus (1) und (2) gilt nach Hippokrates von Chios:
- (3)
- (4)
Es gelten die folgende Streckenverhältnisse:
- (5)
- (6)
Konstruktion der Kantenlänge des verdoppelten Würfels
[Bearbeiten | Quelltext bearbeiten]
Der Halbkreis über dreht sich quasi um den Mittelpunkt entlang der Mantelfläche des (nicht eingezeichneten) Horntorus, bis die Länge der Strecke gleich ist. Dies entspricht dem in der kleinen Skizze dargestellten geometrischen Ansatz des Archytas.
Zwecks Übersichtlichkeit ist der Horntorus im Abschnitt Kurve des Archytas dargestellt. Animation, dazwischen 5 s und am Ende 25 s Pause.
Siehe Animation der Konstruktion
Für eine zeichnerische Darstellung – wie im nebenstehenden Bild – verwendet man eine sogenannte Dynamische Geometrie Software (DGS).[45]
Es beginnt mit dem Zeichnen des Einheitskreises mit Durchmesser . Der anschließende Radius um schneidet den Kreis in Es folgen eine Tangente durch und die Verlängerung der Strecke beide schneiden sich im Punkt Eine Parallele zu ab schneidet den Durchmesser in und den Kreis in
Als Nächstes wird ein kurzer Kreisbogen um mit dem Radius gezogen und darauf der Punkt mit frei wählbarer Position festgelegt. Nach dem Verbinden des Punktes mit ergibt dies die Schnittpunkte auf sowie auf dem Halbkreis . Es folgen ein Halbkreis über und eine Senkrechte auf in , sie ergeben den Schnittpunkt auf dem Halbkreis über . Der nächste Halbkreis über und eine Senkrechte auf in ergeben den Schnittpunkt auf dem Halbkreis – entspricht der Schnittfläche (blau) eines halben Kegels – über Das Errichten des Halbzylinders (Höhe ca. 2,5) über dem Halbkreis schließt sich an.
Es geht weiter mit dem Ziehen eines Kreisbogens um den Punkt mit dem Radius ; er schneidet in die Verlängerung der Kante des Halbzylinders, die zu führt. Nun wird der Punkt mit verbunden. Eine Linie von durch den Punkt bis zum Kreisbogen gezogen ergibt den Schnittpunkt Die Verbindung mit erzeugt das mit dem Dreieck kongruente Dreieck Dies ist möglich, da der Halbkreis über und der Viertelkreis zueinander parallel sind. Betrachtet man im Kontext die beiden ebenfalls kongruenten Dreiecke und sowie den Kreisbogen um so ist das Viertel eines Kegels mit dessen Höhe zu erkennen. Nach dem Verbinden der Punkte mit sowie mit ergeben sich schließlich die beiden maßgeblichen rechtwinkligen Dreiecke und
Der Halbkreis über – die Schnittfläche eines nicht eingezeichneten Horntorus – soll nun um den Punkt so weit gegen den Uhrzeigersinn gedreht werden, bis die Hypotenuse des ebenfalls, aber im Uhrzeigersinn, gedrehten Dreiecks – Schnittfläche des Kegelausschnitts – den Halbkreis über in schneidet. Es ist zu beachten, dass die Strecken und senkrecht aufeinander stehen. Nach dem Höhensatz von Euklid ergibt sich damit
Es folgt aus , dass der Winkel in dieser Stellung gleich ist. Die vier Dreiecke , und sowie sind daher zueinander ähnlich. Die so einregulierte Strecke entspricht der gesuchten Kantenlänge des verdoppelten Würfels, siehe oben.
Der Punkt im Dreieck bestimmt während der Drehung des Halbkreises über die (rote) Kurve des Archytas auf der Mantelfläche des Halbzylinders.
- Für einen exakten Haltepunkt (Punkt trifft auf die Hypotenuse des Dreiecks ) der animierten Drehung des Halbkreises über wird die Strecke mithilfe der DGS[48] bestimmt.
Zwei Parabeln nach Menaichmos
[Bearbeiten | Quelltext bearbeiten]Menaichmos löste das Problem bezüglich Konstruktion der zwei erforderlichen mittleren Proportionen als Schnitt zweier Kegelschnitte (basierend auf Hippokrates’ Umformung des Problems).[49]
Dazu schreibt Johann Christoph Sturm:
(typographisch normalisiert)
„Auflösung.
So nun gegeben sind zwey gerade Lineen AB und BC, zwischen welchen zwey mittlere
gleichverhaltende sollen gefunden werden/ so setze die beyde gegebene winkelrecht auf einander/
und verlängere sie gegen D und E, ohne Maaß/ hinaus; beschreibe so dann/ nach Erforderung
der Lini BC, umb BE eine Parabel/ (also nehmlich/ daß die Vierung einek jeden/ von ihrem
Umbkreiß auf BE senkrecht gezogenen/ Lini (als hier die Vierung EF) gleich sey dem Recht-
ekk aus BC und bem [dem][50] Teihl der Mittel-Lini zwischen B und der vorigen senkrechten (hier BE)
Besihe unten die Anmerkung. Wiederumb beschreibe/ voriger massen/ umb BD, nach
Erforderung der Lini AB eine andere Parabel/ und aus dem Punct F, in welchem sie einander
durchschneiden/ ziehe die senkrechte Lineen FD und FE, so werden BE und BD die begehrte
zwey mittlere gleichverhaltende seyn.“


Parabel und Kreis nach Descartes
[Bearbeiten | Quelltext bearbeiten]Von René Descartes stammt eine etwas einfachere Variation (siehe obiges Bild) zur obigen Lösung von Menaichmos. Um den gleichen Schnittpunkt auf der Parabel bestimmen zu können, benötigt sie, anstatt der zweiten Parabel, einen Kreis um mit Radius .[52]
Zissoide des Diokles
[Bearbeiten | Quelltext bearbeiten]
Diokles löste das Problem der beiden mittleren Proportionalen mit der nach ihm benannten Kurve, auch bekannt als Kissoide des Diokles.
Bezeichnet man die beiden Proportionalen mit und so ergibt sich als zu lösendes Konstruktionsproblem „die doppelte Proportion zwischen a und 2a“.[15]
Darin ist die gesuchte Seitenlänge (im Bild 2 mit bezeichnet), es gilt
Vorüberlegung
[Bearbeiten | Quelltext bearbeiten]
Die kartesischen Koordinaten der Zissoide sind z. B.
Die Konstruktion wird vereinfacht, wenn der Wert des Faktors in den kartesischen Koordinaten der Zissoide gleich dem der Kantenlänge des Ausgangswürfels ist. Es wird nur der Teil des Graphen der Zissoide benötigt, der im 1. Quadranten eines kartesischen Koordinatensystems liegt.
Vorgehensweise
[Bearbeiten | Quelltext bearbeiten]Es sei der Koordinatenursprung, der Mittelpunkt des Halbkreises mit beliebigem Radius und der Durchmesser.
Um einen Punkt auf der Zissoide zu bestimmen (siehe Bild 1), bedarf es der zwei Parallelen und . Sie stehen senkrecht auf dem Durchmesser und haben aufgrund des Halbkreises die gleiche Länge sowie den gleichen Abstand zum Mittelpunkt . Wird die Parallele bewegt, so liefert die Halbgerade ab mithilfe des Punktes – entweder direkt auf der Parallelen oder auf deren Verlängerung – den auf der Zissoide liegenden Punkt .
Eine kontinuierliche Veränderung des Abstandes der beiden Parallelen und zueinander erzeugt, wegen des dadurch bewegten Punktes , im Koordinatenursprung den Graphen der Zissoide im 1. Quadranten.
Es geht weiter (siehe Bild 2) mit der auf dem Durchmesser senkrecht stehenden Strecke mit der Länge gleich Die Verbindung des Punktes mit schneidet den Graphen der Zissoide in Die abschließende Verbindung des Punktes mit liefert mit die gesuchte Seite des verdoppelten Würfels.
Die parallel zu strichliert eingezeichnete Strecke dient lediglich der Beweisführung.[15]
Parabel nach J. Bolyai
[Bearbeiten | Quelltext bearbeiten]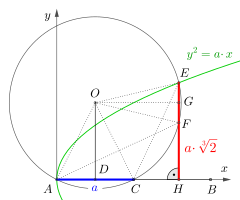
Johann Bolyai machte während seiner Studienzeit (1817–1822) Aufzeichnungen über die Winkeldreiteilung (1898 von Paul Stäckel gefunden) und wie erst später entdeckt, auch zur Würfelverdoppelung. Sein Hauptaugenmerk lag insbesondere auf das n-malige Vervielfachen des Volumens eines Ausgangswürfels. Er generierte dazu Lösungen mithilfe einer Hyperbel, zweier Parabeln sowie mit einer von ihm entwickelten Zissoide. Dabei fand er auch eine offensichtlich sehr einfache Lösung zur Verdoppelung, die mit einer einzigen Parabel, wie im Folgenden beschrieben, auskommt.[54]
Die Aufzeichnungen darüber veröffentlichte Róbert Oláh-Gál im Jahr 2007 in einem Aufsatz. Er weist darauf hin, dass die von Bolyai verwendeten Bezeichnungen auf den heutigen Gebrauch umgeschrieben, und wo es nötig war, ergänzt wurden.[54]
Vorgehensweise
In einem kartesischen Koordinatensystem wird zuerst auf die x-Achse, ab dem Koordinatenursprung die Seitenlänge des Ausgangswürfels zweimal abgetragen; dabei ergeben sich die Strecken und . Nach der Halbierung der Strecke in folgt das Errichten der senkrechten Strecke auf . Der Kreis um durch die Punkte und schließt sich an. Abschließend wird die Parabel generiert; dabei ergibt sich der Schnittpunkt , und das Lot auf mit dem Fußpunkt gefällt. Die so gefundene Strecke ist die Seitenlänge des verdoppelten Würfels.
Die gepunkteten Linien sowie die Punkte und sind nicht Teil der Lösung, sie dienen lediglich für den Beweis nach Oláh-Gál.[55]
Logarithmische Verdoppelungsspirale
[Bearbeiten | Quelltext bearbeiten]
Eine sichtbar einfache Methode beschreibt Hans Walser in Spiralen, Schraubenlinien und spiralartige Figuren aus dem Jahr 2022. Sie benötigt nicht das Bestimmen von zwei mittleren Proportionalen zweier Größen, sondern nutzt als zusätzliches Hilfsmittel eine sogenannte logarithmische Verdoppelungsspirale mit der Eigenschaft: Bei jeder Umdrehung um ihren Mittelpunkt (Zentrum, Pol) verändert sich der Abstand von diesem Mittelpunkt um den Faktor .[56]
Gegeben ist der Ausgangswürfel mit der Seitenlänge (grün). Die zur Verdoppelung geeignete logarithmische Spirale (rot) hat die kartesischen Koordinaten:
Das Zentrum der Spirale liegt im Koordinatenursprung . Die Spirale startet auf der x-Achse im Punkt , schneidet die x-Achse im Punkt und endet in diesem Fall kurz nach dem Schneiden der x-Achse im Punkt .
Die eigentliche Konstruktion hat nur zwei Hauptschritte. Zuerst wird mithilfe einer Halbgeraden der Winkel zur x-Achse mit Scheitelpunkt bestimmt (Drehung der 2. Windung beginnt ab Punkt 1), bis diese die Spirale im Punkt schneidet. Die Länge ist die gesuchte Seitenlänge des verdoppelten Würfels. Abschließend projiziert man den Punkt auf die x-Achse, ergibt , und zeichnet den verdoppelten Würfel ein.
Die Strecke (grau) hat die Länge . Das entspricht der Seitenlänge eines – nicht eingezeichneten – halbierten Ausgangswürfels.
- Nachrechnung
In Polarkoordinaten ergibt sich:
- (1).
Darin sind der Abstand vom Ursprung (Pol) zum Punkt auf der Spirale, der Winkel () relativ zur x-Achse, die Startposition der relevanten Windung auf der x-Achse, die Steigung der Spirale und die Eulersche Zahl.
Gegeben: , Spirale mit entspricht , Drehung der 2. Windung ab Punkt der x-Achse bis auf Punkt
Gesucht: und (Strecke )
Werte zum Bestimmen der Steigung in Gleichung (1) eingesetzt
- , nach dem Logarithmieren erhält man
- (2),
Werte für und in Gleichung (1) eingesetzt
- (3), wegen
- , ergibt sich schließlich
- .
Nach einer Drehung der 2. Windung, ab Punkt der x-Achse, ist die gesuchte Länge (Strecke ) gleich .
Für die Länge (Strecke ) ergibt sich mit dem Winkel
- .
Würfelverdoppelung mit Origami
[Bearbeiten | Quelltext bearbeiten]Die Verdoppelung des Würfels kann auch – so wie die Dreiteilung des Winkels – mit dem zusätzlichen Hilfsmittel Origami konstruiert werden. Verwendet wird hierfür ein quadratisches oder rechteckiges Blatt Papier.[57]
Beim fertigen Origami ist zu berücksichtigen, dass das Ergebnis der Faltungen nicht die Kantenlänge eines vorgegebenen Ausgangswürfels berücksichtigt. Das Ergebnis zeigt eine Strecke, die im Verhältnis geteilt ist und deren Längenwerte unbekannt sind. Erst die anschließende sogenannte zentrische Streckung mit der vorgegebenen Kantenlänge des Ausgangswürfels als Basis, liefert die gesuchte Kantenlänge des verdoppelten Würfels.
Vorgehensweise
[Bearbeiten | Quelltext bearbeiten]Um drei gleiche Teile der Blatthöhe als Faltlinien zu erhalten, wird zuerst das Blatt in der Mitte gefaltet (siehe Bild 1); dabei ergeben sich an den beiden Blattkanten und die Punkte bzw. . Es folgen die diagonale Falte und die Falte sie schneiden sich im Punkt Die nächste Falte durch den Punkt und parallel zur Blattkante bestimmt das erste Drittel der Blatthöhe; dabei ergeben sich an den beiden Blattkanten und die Punkte bzw. . Für das zweite und dritte Drittel der Blatthöhe legt man die Blattkante auf die Falte dabei ergeben sich an den beiden Blattkanten und die Punkte bzw. .
Als Nächstes wird die Falte so gelegt (siehe Bild 2), dass die Ecke des Blattes auf der Kante und der Punkt auf der Falte zum Liegen kommt. Somit teilt die Strecke im Verhältnis
Für das Bestimmen der Kantenlänge (siehe Bild 3) bedarf es – wie oben begründet – der Übertragung der Strecke inklusive des Teilungspunktes (von Bild 2) als Orthogonale (Senkrechte) auf eine Geraden , einer ebenfalls senkrecht zu angeordneten Kantenlänge des Ausgangswürfels (grün) sowie des Punktes (von Bild 2) auf Es folgt ein Strahl ab dem Punkt durch bis er die Maßhilfslinie der Kantenlänge in schneidet. Anschließend wird im Punkt eine Senkrechte auf die Maßhilfslinie errichtet. Der abschließende zweite Strahl ab durch liefert die Strecke mit der Länge als die gesuchte Kantenlänge des verdoppelten Würfels.
-
Bild 1
Blatthöhe in drei gleich Teile falten -
Bild 2
-
Bild 3
Konstruktion der Kantenlänge des verdoppelten Würfels mithilfe der vorgegebenen Kantenlänge des Ausgangswürfels
Iterative Näherungskonstruktion der Kubikwurzel aus 2
[Bearbeiten | Quelltext bearbeiten]Aus oben bereits beschriebenen Gründen kann das Ergebnis der Kubikwurzel nicht mit Zirkel und Lineal mit endlichen Konstruktionsschritten exakt dargestellt werden.
Einen Weg für sehr gute Näherungen ermöglicht das Newtonverfahren.[58] Im Folgenden wird es verwendet, um für die Würfelverdoppelung die reelle Nullstelle der Funktion
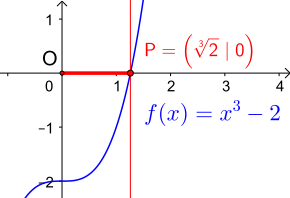
als Näherung mit wenigen Iterationsschritten zu erreichen.
Als Startwert kann genommen werden. Die Iterationsschritte des Algorithmus sind durch
definiert.
Weil der Ausdruck für nur die Grundrechenarten enthält, lässt sich das Ergebnis jedes Iterationsschritts als Strecke mit Zirkel und Lineal konstruieren.
Berechnung der Iterationsschritte
[Bearbeiten | Quelltext bearbeiten]In der Formel
liefert der Term auf der rechten Seite der Gleichung das Ergebnis des -ten Iterationsschrittes. Ein Iterationsschritt setzt sich aus sechs algebraische Operationen zusammen, von denen stets die Fünfte der Zähler und die Zweite der Nenner eines unechten Bruchs sind.
1. Iterationsschritt , fünf Operationen haben z. B. eingesetzter Wert für

entspricht dem 1. Iterationsschritt mit sowie
dem 3. Iterationsschritt mit
Der nicht eingezeichnete 2. Iterationsschritt mit liegt bereits sehr nahe an
2. Iterationsschritt , fünf Operationen haben z. B. eingesetzter Wert für
3. Iterationsschritt , fünf Operationen haben z. B. eingesetzter Wert für
Dieser Ablauf lässt sich beliebig oft wiederholen. Es liegt quadratische Konvergenzgeschwindigkeit vor, was das Verfahren vergleichsweise effizient macht.
Konstruktion mit Zirkel und Lineal
[Bearbeiten | Quelltext bearbeiten]Bereits nach zwei Iterationsschritten ist die Effizienz der Anwendung des Newtonverfahrens gut erkennbar, der bis dahin erreichte Näherungswert ist Es folgt nun eine konstruktive Weiterführung bis zum Erreichen des 3. Iterationsschritts mit dem Näherungswert .
Zuerst wird der unechte Bruch umformuliert in den (unechten) Dezimalbruch und anschließend als exakte Länge auf einer Zahlengerade (Bild 1) abgebildet. Dazu eignet sich z. B. die Methode Konstruktion einer Dezimalzahl mithilfe des 3. Strahlensatzes. Wegen der Größenverhältnisse ist es von Vorteil, dies in einem eigenen Bild zu zeigen.
Im nächsten Schritt wird die Länge (rot) aus Bild 1 in das Bild 2 (grün, Ziffer 2) übertragen. Es folgt das Bestimmen der Quadratzahl (Ziffer 3) und der Kubikzahl (Ziffer 4) von Im fünften Schritt wird die Kubikzahl von mit dem Faktor multipliziert und die Zahl addiert. Abschließend (Ziffer 6) wird der Quotient (rot) ermittelt:
Beispiel, um den Fehler zu verdeutlichen
Bei einem Ausgangswürfel mit der Kantenlänge m wäre die Kante des nur näherungsweise verdoppelten Würfels ca. mm zu lang.
- Nur einen Iterationsschritt mehr, sprich mit den Operationen 7–11 in einem Bild 3, würde man bereits den sehr genauen Wert (vergleiche Sollwert) erhalten.[59]
- Damit wäre bei einem Ausgangswürfel mit der Kantenlänge km die Kante des nur näherungsweise verdoppelten Würfels ca. mm zu lang.[60]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Arthur Donald Steele: Über die Rolle von Zirkel und Lineal in der griechischen Mathematik. In: Quellen und Studien zur Geschichte der Mathematik. Abteilung B, Band 3, 1936, S. 287–369 (harvard.edu [PDF; 8,8 MB]).
- Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid (= Science, Technology, and Medicine in Ancient Cultures. Band 9). Walter de Gruyter, Berlin/Boston 2019, S. 177–270 (eingeschränkte Vorschau in der Google-Buchsuche).
- Markus Asper: Mathematik. Die griechische Mathematik bis zum Ende des Hellenismus. In: Bernhard Zimmermann, Antonios Rengakos (Hrsg.): Handbuch der griechischen Literatur der Antike. Band 2: Die Literatur der klassischen und hellenistischen Zeit (= Handbuch der Altertumswissenschaft. Band 7,2). C.H.Beck, München 2014, S. 459–481 (Vorschau in der Google-Buchsuche).
- Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. In: Historia Mathematica. 36, 2009, S. 374–394, doi:10.1016/j.hm.2009.03.001.
- Walter Breidenbach: Das Delische Problem (Die Verdoppelung des Würfels), 1952, DEUTSCHE DIGITALE BIBLIOTHEK
- Frédéric Beatrix, Peter Katzlinger: A pretty accurate solution to the Delian problem. In: Parabola Volume 59 (2023) Issue 1, online magazine (ISSN 1446-9723) published by the School of Mathematics and Statistics University of New South Wales
Weblinks
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Reviel Netz: The Works of Archimedes, Translated into English, together with Eutocius’ commentaries, ... Band 1: The Two Books On the Sphere and the Cylinder. Cambridge University Press, New York 2004, ISBN 0-521-66160-9, S. 270–306 (pyrkov-professor.ru [PDF]).
- ↑ Zur Echtheit des bei Eutokios überlieferten Brieftextes W. R. Knorr: The Ancient Tradition of Geometric Problems. Boston 1986, S. 17–24. Zur Frage, welcher König Ptolemaios gemeint ist, siehe etwa W. R. Knorr: Textual Studies in Ancient and Medieval Geometry. Boston 1989, S. 144 f.
- ↑ a b c Reviel Netz: The Works of Archimedes, Translated into English, together with Eutocius’ commentaries, ... Band 1: The Two Books On the Sphere and the Cylinder. Cambridge University Press, New York 2004, ISBN 0-521-66160-9, S. 294 (pyrkov-professor.ru [PDF]).
- ↑ Richard Kannicht, Bruno Snell: Tragicorum Graecorum Fragmenta. 2. Auflage. Band 2. Vandenhoeck & Ruprecht, Göttingen 2007, S. 62, Fragment Adespota F 166; zur Behandlung des Glaukos-Stoffes bei den Tragödiendichtern siehe Georg Weicker: Glaukos 23. In: Paulys Realencyclopädie der classischen Altertumswissenschaft (RE). Band VII,1, Stuttgart 1910, Sp. 1415 f.
- ↑ Eine ausführliche Analyse des antiken Quellenmaterials zur Delier-Anekdote und den möglichen historischen Grundlagen bietet Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid (= Science, Technology, and Medicine in Ancient Cultures. Band 9). De Gruyter, Berlin/Boston 2019, S. 187–206; zu den drei mechanischen Ansätzen und Platons Kritik ebd., S. 220–241.
- ↑ Reviel Netz: The Works of Archimedes, Translated into English, together with Eutocius’ commentaries, ... Band 1: The Two Books On the Sphere and the Cylinder. Cambridge University Press, New York 2004, ISBN 0-521-66160-9, S. 273, Anmerkung 17 (pyrkov-professor.ru [PDF]).
- ↑ Zum Beispiel Joseph: The crest of the peacock. Princeton UP, 2001, S. 330.
- ↑ Horst Hischer: Moritz Cantor und die krumme Linie des Archytas von Tarent. In: Lisa Hefendehl-Hebeker, Stephan Hußmann (Hrsg.): Mathematikdidaktik zwischen Fachorientierung und Empirie. Festschrift für Norbert Knoche. Franzbecker, Hildesheim/Berlin 2003, ISBN 3-88120-364-8, S. 74 (uni-sb.de [PDF; 1,6 MB; abgerufen am 25. Juli 2022]).
- ↑ a b Horst Hischer: Moritz Cantor und die krumme Linie des Archytas von Tarent. In: Lisa Hefendehl-Hebeker, Stephan Hußmann (Hrsg.): Mathematikdidaktik zwischen Fachorientierung und Empirie. Festschrift für Norbert Knoche. Franzbecker, Hildesheim/Berlin 2003, ISBN 3-88120-364-8, S. 78 (uni-sb.de [PDF; 1,6 MB; abgerufen am 25. Juli 2022]).
- ↑ Horst Hischer: 5.1 Lösungswerkzeug: Holzrahmen-Apparat (vermutlich von Eratosthenes). Zum Problem der Würfelverdoppelung in der Darstellung durch Johann Christoph Sturm 1670. Hrsg.: Universität des Saarlandes. Saarbrücken 2015, S. 5 (uni-sb.de [PDF; 1,3 MB; abgerufen am 25. Juli 2022]).
- ↑ François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos. Berlin 1966, S. 20–22, 163–166.
- ↑ Horst Hischer: 6.1 Lösungsweg: Schnittpunkt von zwei Parabeln nach Menaichmos. Zum Problem der Würfelverdoppelung in der Darstellung durch Johann Christoph Sturm 1670. Hrsg.: Universität des Saarlandes. Saarbrücken 2015, S. 9 (uni-sb.de [PDF; 1,3 MB; abgerufen am 25. Juli 2022]).
- ↑ Reviel Netz: The Works of Archimedes, Translated into English, together with Eutocius’ commentaries, ... Band 1: The Two Books On the Sphere and the Cylinder. Cambridge University Press, New York 2004, ISBN 0-521-66160-9, S. 295 (pyrkov-professor.ru [PDF]).
- ↑ Horst Hischer: 5.2 Lösungswerkzeug: das Mesolabium des Eratosthenes. Zum Problem der Würfelverdoppelung in der Darstellung durch Johann Christoph Sturm 1670. Hrsg.: Universität des Saarlandes. Saarbrücken 2015, S. 7 (uni-sb.de [PDF; 1,3 MB; abgerufen am 25. Juli 2022]).
- ↑ a b c d Pascal Praß, Adrian De Lont: Würfelverdoppelung mit der Kissoiden. (PDF) Allgemeine Kissoiden, Seminar über höhere Kurven. Universität Mainz, 2016, S. 12, abgerufen am 5. Juli 2021.
- ↑ A. D. Steele: Über die Rolle von Zirkel und Lineal in der griechischen Mathematik. In: Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik. Band B 3, 1936, S. 287–369 (auch speziell zum Problem der Würfelverdopplung).
- ↑ Pierre Wantzel: Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas (= Journal de mathématiques pures et appliquées (Liouville’s Journal). Band 2). 1837, S. 366–372 (bnf.fr [PDF]).
- ↑ Adhémar Jean Claude Barré de Saint-Venant: Biographie. Wantzel. In: Nouvelles Annales de Mathématiques. Série 1. Band 7, 1848, ZDB-ID 426713-8, S. 321–331, S. 329: Publikationen im Journal des mathématiques pures (französisch, numdam.org [PDF; 780 kB; abgerufen am 10. April 2021]).
- ↑ Jesper Lützen:: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. (PDF) In: Historia Mathematica 36. Universität W&M, 28. Oktober 2009, S. 378–379, abgerufen am 31. Mai 2022 (englisch).
- ↑ Jesper Lützen:: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. (PDF) In: Historia Mathematica 36. Universität W&M, 28. Oktober 2009, S. 379, abgerufen am 31. Mai 2022 (englisch).
- ↑ Jesper Lützen:: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. (PDF) In: Historia Mathematica 36. Universität W&M, 28. Oktober 2009, S. 391, abgerufen am 31. Mai 2022 (englisch).
- ↑ Jesper Lützen:: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. (PDF) In: Historia Mathematica 36. Universität W&M, 28. Oktober 2009, S. 387, abgerufen am 31. Mai 2022 (englisch).
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie. 3. Auflage. Springer-Verlag, Berlin/Heidelberg 2010, ISBN 978-3-642-02361-3, S. 405.
- ↑ Falko Lorenz: Algebra Volume I: Fields and Galois Theory, Springer, S. 6–13.
- ↑ a b Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid. 5.3 Platons Würfelverdopplung und der mechanische Beweis (= Science, Technology, and Medicine in Ancient Cultures. Band 9). Walter de Gruyter, Berlin/Boston 2019, ISBN 978-3-11-061382-7, S. 213 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Klaus Volkert: Geschichte der geometrischen Konstruktionsprobleme I. (PDF; 1,5 MB) In: Vorlesung, Universität zu Köln im WS 06/07; […] Siebeneck. Universität Wuppertal, 2006, S. 20, abgerufen am 15. September 2018.
- ↑ Heinrich Dörrie: 35. The Delian Cube-doubling Problem. In: 100 Great Problems of Elementary Mathematics. New York, Dover Publications, Inc., 1965, S. 170–171, abgerufen am 5. Mai 2019.
- ↑ Isaac Newton, Übersetzer Ralphson: Universal Arithmetick: Or, A Treatise of Arithmetical Composition and Resolution. In: Appentix. The Linear Construction of Equations . 1728, S. 242 (eingeschränkte Vorschau in der Google-Buchsuche) Letzter Absatz, Tab: VII, Fig. 99, abgerufen am 24. März 2022.
- ↑ David M. Burton: The History of Mathematics. Three Construction Problems of Antiquity. 7. Auflage. New York 2011, ISBN 978-0-07-338315-6, 3.4 Problems, S. 129 (englisch, illinois.edu [PDF; 11,2 MB; abgerufen am 2. April 2024]).
- ↑ Albrecht Dürer: Underweysung der messung mit dem zirckel un[d] richtscheyt, in Linien ebnen unnd gantzen corporen. SLUB, Digitale Sammlungen, 1525, S. 157–158, abgerufen am 24. Mai 2022.
- ↑ Für eine bessere Vergleichbarkeit sind Schriftform und Bezeichnungen aus der Quelle übernommen.
- ↑ a b Bodo v. Pape: Von Eudoxus zu Uhlhorn: Die Lösungen zu den Großen Problemen der Antike. BoD–Books on Demand, 2019, ISBN 978-3-7494-6204-9, S. 91–92 (6.7 Die Lösung „Sporus“ in der Google-Buchsuche).
- ↑ Bodo v. Pape: Von Eudoxus zu Uhlhorn: Die Lösungen zu den Großen Problemen der Antike. BoD–Books on Demand, 2019, ISBN 978-3-7494-6204-9, S. 91 (6.7 Die Lösung „Sporus“ in der Google-Buchsuche).
- ↑ a b c Horst Hischer: Moritz Cantor und die krumme Linie des Archytas von Tarent. (PDF; 1,5 MB) Universität des Saarlandes, 2003, S. 76, abgerufen am 30. Oktober 2020.
- ↑ a b Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid. 5.3 Platons Würfelverdopplung und der mechanische Beweis (= Science, Technology, and Medicine in Ancient Cultures. Band 9). Walter de Gruyter, Berlin/Boston 2019, ISBN 978-3-11-061382-7, S. 215 ff. (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid. 5.23 Die archäologische und historische Perspektive (= Science, Technology, and Medicine in Ancient Cultures. Band 9). Walter de Gruyter, Berlin/Boston 2019, ISBN 978-3-11-061382-7, S. 199–212 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid, 5 Platon und das Delische Problem, 5.2.4 Fazit. Walter de Gruyter, Berlin/Boston 2019, S. 207, letzter Absatz (eingeschränkte Vorschau in der Google-Buchsuche)
- ↑ Euklid: Elemente Stoicheia. Buch 1, Proposition 29. Edition Opera-Platonis, Markgröningen 2017, S. 17 (opera-platonis.de [PDF; 469 kB; abgerufen am 12. April 2021]).
- ↑ Euklid: Elemente Stoicheia. Buch 1, Proposition 32. Edition Opera-Platonis, Markgröningen 2017, S. 19 (opera-platonis.de [PDF; 469 kB]).
- ↑ Euklid: Elemente Stoicheia. Buch 6, Proposition 4. Edition Opera-Platonis, Markgröningen 2017, S. 4 (opera-platonis.de [PDF; 529 kB; abgerufen am 11. April 2021]).
- ↑ Übersetzung nach Claas Lattmann: Mathematische Modellierung bei Platon zwischen Thales und Euklid. Walter de Gruyter, Berlin/Boston 2019, ISBN 978-3-11-061382-7, S. 182 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Reviel Netz: The Works of Archimedes, Translated into English, together with Eutocius’ commentaries, ... Band 1: The Two Books On the Sphere and the Cylinder. Cambridge University Press, New York 2004, ISBN 0-521-66160-9, S. 294–298 (pyrkov-professor.ru [PDF]).
- ↑ Bartel Leendert van der Waerden: Science Awakening. 1956, 230 f. Drei Rechtecke oder Dreiecke, die längs eines Lineals verschoben werden konnten, dessen eine Seite frei drehbar war.
- ↑ a b Thomas Heath: A History of Greek Mathematics. The Duplication Of The Cube, (ζ) Eratosthenes. Band 1. The Clarendon Press, Oxford 1921, S. 259 (englisch, Scan – Internet Archive).
- ↑ a b Horst Hischer: Moritz Cantor und die krumme Linie des Archytas von Tarent. (PDF; 1,5 MB) Universität des Saarlandes, 2003, S. 79 ff., abgerufen am 1. November 2020.
- ↑ Weisstein, Eric W.: Horn Torus. WolframMathWorld, abgerufen am 30. Mai 2022.
- ↑ Rudolf Stopfer: Die Verdoppelung des Würfels, 5. Lösung nach Archytas. Seminar: Klassische Probleme der Antike. Universität Bayreuth, 8. Juni 1997, archiviert vom (nicht mehr online verfügbar) am 27. Februar 2021; abgerufen am 8. März 2022.
- ↑ Didaktik der Mathematik, Dynamische Geometriesoftware. Universität Würzburg, abgerufen am 4. August 2021.
- ↑ Horst Hischer: 6.1 Lösungsweg: Schnittpunkt von zwei Parabeln nach Menaichmos. (PDF; 1,2 MB) Zur Darstellung des Problems der Würfelverdoppelung durch Johann Christoph Sturm 1670. Universität Saarland, 2015, S. 9–10, abgerufen am 1. Mai 2019 (Preprint Nr. 367).
- ↑ Emendation ergibt sich aus dem Satzzusammenhang.
- ↑ Johann Christoph Sturm: Der zweyte kunſtrichtige oder Geometriſche Weg … [Der zweyte kunstrichtige oder Geometrische Weg …] In: Des Unvergleichlichen ARCHJMEDJS Kunſt-Bücher. [Des Unvergleichlichen ARCHIMEDIS Kunst-Bücher.] Nürnberg 1670. DTA Deutsches Textarchiv, S. 118 ff., hier S. 119, urn:nbn:de:kobv:b4-20590-8 (Digitalisat und Volltext im Deutschen Textarchiv, abgerufen am 2. November 2020).
- ↑ Horst Hischer: 6.2 Lösungsweg: Schnittpunkt von einer Parabel mit einem Kreis nach Descartes. (PDF) Zur Darstellung des Problems der Würfelverdoppelung durch Johann Christoph Sturm 1670. Universität Saarland, 2015, S. 10, abgerufen am 4. September 2024 (Preprint Nr. 367).
- ↑ Pascal Praß, Adrian De Lont: Würfelverdoppelung mit der Kissoiden. (PDF) Allgemeine Kissoiden, Seminar über höhere Kurven. Universität Mainz, 2016, S. 9, abgerufen am 5. Juli 2021.
- ↑ a b Róbert Oláh-Gál: Die aus der Studienzeit stammenden Aufzeichnungen des Johann Bolyai über die Würfelverdoppelung. (PDF) researchgate.net, 16. Februar 2007, S. 3, abgerufen am 12. Januar 2022.
- ↑ Róbert Oláh-Gál: Die aus der Studienzeit stammenden Aufzeichnungen des Johann Bolyai über die Würfelverdoppelung. (PDF) researchgate.net, 16. Februar 2007, S. 7, abgerufen am 12. Januar 2022.
- ↑ Hans Walser: Spiralen, Schraubenlinien und spiralartige Figuren - Mathematische Spielereien in zwei und drei Dimensionen, 2.9 Würfelverdoppelung mit Stern und Spirale Springer Spektrum, Springer-Verlag GmbH Berlin 2022, ISBN 978-3-662-65131-5, Seiten 25–28
- ↑ Michael Strobl: Lösungen von Konstruktionsproblemen durch Origami. (PDF) In: Konstruktion mit Zirkel und Lineal vs. Origami. Universität Innsbruck, 2018, S. 56–60, abgerufen am 4. November 2021.
- ↑ Daniel Mathews, Sue Finch u. a.: Newton's method. In: AMSI. 2. August 2019, abgerufen am 16. Mai 2022 (englisch).
- ↑ 4. Iterationsschritt auf wolframalpha.com.
- ↑ Absoluter Fehler von auf wolframalpha.com.





![{\displaystyle {\sqrt[{3}]{2}}=1{,}259921\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4058bbfb35a02631b34c9d9449efd8b9952633)
![{\displaystyle a={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b02de6ae656efbfa6bc25257931c87610a93cc)




![{\displaystyle x={\sqrt[{3}]{2}}\cdot a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8806b3b210d5b5b3faab975b558761c2a98cf0fd)

![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)









![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)



![{\displaystyle {\sqrt[{3}]{2}}=1{,}2599210498948732...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c823b1fddc8d0c81eaec2cf50de97e3f50785c1e)


















![{\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]=3\not =2^{n}\qquad {\text{für alle}}\,n\in \mathbb {N} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78baa1ec4584c13e6128616e5b344e7b5fa7b87f)
![{\displaystyle \mathbb {Q} ({\sqrt[{3}]{2}})|\mathbb {Q} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5803afab02e9215c8a3525b22d67818bf3ed380b)


![{\displaystyle \mathbb {Q} ({\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4682c6f3952f1b35a5db23be9b806fc79e771d30)
![{\displaystyle a+b{\sqrt[{3}]{2}}+c{\sqrt[{3}]{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72434841a928d9a64f39067ea7755fd32a49954)

![{\displaystyle {\frac {{\sqrt[{3}]{2}}+2}{{\sqrt[{3}]{2}}-1}}=4+3\cdot {\sqrt[{3}]{2}}+3\cdot {\sqrt[{3}]{4}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cafd9be4a02089bc5c580ffe97f9be4a2d30a955)














![{\displaystyle {\overline {CQ}}=k\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/107bcbe2f4a8c54b1ab5860bce100ad6ffa8a14b)







![{\displaystyle a:x=b:y=c:a={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aba0e2e729a1940baffb3949e035ef2489860270)



![{\displaystyle {\overline {AC}}=a\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/403c28421871364a981e34dcbacb7888ea8c46a5)


















![{\displaystyle {\sqrt[{2}]{\mathrm {B\Theta } \cdot \mathrm {B\Gamma } }}=\mathrm {\Xi } =a\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ae4734fde88f753d37803d40c58103d7b8af872)











![{\displaystyle \mathrm {B\Theta } ={\sqrt[{3}]{2}}^{2}=2^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f22f430bd883f8c87bfcbae46de3d6fab53987a9)
![{\displaystyle \mathrm {\Xi } ={\sqrt {2^{2/3}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2978477598a240cb4f87ca09206522a01ab554e2)
![{\displaystyle 2:2^{2/3}=2^{2/3}:{\sqrt[{3}]{2}}={\sqrt[{3}]{2}}:1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada20c32852dcfaaf7297d083ca39198d26e2f47)
![{\displaystyle \mathrm {\sqrt[{3}]{2}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/28335cd05b9aab1909dfa364a66320f53a6b4153)

























![{\displaystyle |{\overline {CK}}|={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c33b3feab756a783211aa0104b53973ad0faa28)


![{\displaystyle |{\overline {CH'}}|={\sqrt[{3}]{2}}^{2}=2^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee11e6e3bb40cf338120e8cf44dffd170ef42ff)










![{\displaystyle |{\overline {HD}}|={\sqrt {|{\overline {DC}}|^{2}+|{\overline {CH}}|^{2}}}={\sqrt {4+2^{4/3}}}={\sqrt {4+2{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe028181a2e59237ea1229d66acb17d6687ea88c)

![{\displaystyle {\overline {RH}}={\frac {{\overline {CH}}\cdot {\overline {HD}}}{\overline {DC}}}={\frac {2^{2/3}\cdot {\sqrt {4+2{\sqrt[{3}]{2}}}}}{2}}={\frac {\sqrt {4+2{\sqrt[{3}]{2}}}}{\sqrt[{3}]{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7469c2b0044ae23c7c2aa4d3758ecb14934a22d4)
![{\displaystyle {\overline {DR}}={\frac {{\overline {RH}}\cdot {\overline {HD}}}{\overline {CH}}}={\frac {{\frac {\sqrt {4+2{\sqrt[{3}]{2}}}}{\sqrt[{3}]{2}}}\cdot {\sqrt {4+2{\sqrt[{3}]{2}}}}}{2^{2/3}}}={\frac {1}{2}}\left(4+2{\sqrt[{3}]{2}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8984d68317b8d6fe35c1fc8e3fc2fd160bb7962)


![{\displaystyle {\overline {ID}}={\frac {{\overline {DE}}\cdot {\overline {HD}}}{\overline {DR}}}={\frac {4{\sqrt {4+2{\sqrt[{3}]{2}}}}}{{\frac {1}{2}}\left(4+2{\sqrt[{3}]{2}}\right)}}={\frac {8}{\sqrt {4+2{\sqrt[{3}]{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f4f3200bbf38cefb3ca6a32cc21a983868df301)


![{\displaystyle {\overline {GD}}=2\cdot {\overline {HD}}-{\overline {ID}}=2\cdot {\sqrt {4+2{\sqrt[{3}]{2}}}}-{\frac {8}{\sqrt {4+2{\sqrt[{3}]{2}}}}}={\frac {4{\sqrt[{3}]{2}}}{\sqrt {2\left(2+{\sqrt[{3}]{2}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ee064da464ebda36cf0461d76360e3e7863d04)

![{\displaystyle {\overline {DS}}={\frac {{\overline {DR}}\cdot {\overline {GD}}}{\overline {HD}}}={\frac {{\frac {1}{2}}\left(4+2{\sqrt[{3}]{2}}\right)\cdot {\tfrac {4{\sqrt[{3}]{2}}}{\sqrt {2\left(2+{\sqrt[{3}]{2}}\right)}}}}{\sqrt {4+2{\sqrt[{3}]{2}}}}}=2{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be9d0adada816f0e3354bd6cbfd1d65e5b5cb65)
![{\displaystyle {\overline {SR}}={\overline {DR}}-{\overline {DS}}={\frac {1}{2}}\left(4+2{\sqrt[{3}]{2}}\right)-2{\sqrt[{3}]{2}}=2-{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87933fb447a5b053dea53f3598891c69b2741a45)
![{\displaystyle {\overline {RE}}={\overline {DE}}-{\overline {DR}}=4-{\frac {1}{2}}\left(4+2{\sqrt[{3}]{2}}\right)=2-{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ef8a85fe7b05d865af6fe2757f450d3ff12029)

![{\displaystyle a\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3368a7d04c7a3465047ebe3bfded7aeb5d9471ef)








![{\displaystyle {\overline {\Delta E}}={\sqrt {y^{2}+x^{2}}},\,\,{\overline {AE}}={\sqrt {4a^{2}+y^{2}}},\,\,x=a\cdot {\sqrt[{3}]{2}}\,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87101a01f26469ba01373eda008f9df548c485e)
![{\displaystyle \,\,y={\frac {2a}{\sqrt[{3}]{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c5c80148d9d5bebacb157da7c9ea025afb91a8c)





![{\displaystyle {\overline {B\Delta }}:{\overline {B\Gamma }}={\overline {AB}}:{\overline {BE}}={\overline {BE}}:{\overline {B\Delta }}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45f179abc6203a1f5c8946bd4bfb1ed372462f4c)



























![{\displaystyle x=a\cdot {\sqrt[{3}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f55473f21840034b97fcca3d688f344f8f0452ea)
![{\displaystyle y={\frac {2a^{2}}{a\cdot {\sqrt[{3}]{2}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cf7d9ad0bd969c47e54095c5a555721e1c141f3)
![{\displaystyle y={\frac {2a}{\sqrt[{3}]{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c21a162fe89a90b2e7f4324deb01bf6bdf24b)



















![{\displaystyle {\overline {AD'}}:{\overline {AK}}={\overline {AI}}:{\overline {AM}}={\overline {AK}}:{\overline {AI}}=y:x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a893191ddc339796b29ebb76e3728e4707000f9)



































![{\displaystyle {\overline {AI}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f79389e6ab80ff55fb69871045a529940bd9768)




![{\displaystyle x:a=y:x=b:y={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126b8b7b2adae65688facbd5d808867a0790f004)



















![{\displaystyle v=a\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a3846f3b93f73c80131a614bdd5edc9a31a3c8)







![{\displaystyle {\overline {EH}}=a\cdot {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b479dda2691afe8ab00953e8858961588ce07f2)





![{\displaystyle {\tfrac {1}{\sqrt[{3}]{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aa4bcca07e05dce2419d9e6a595e8a0d6fc69bd)















![{\displaystyle \;r=2^{\frac {1}{3}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f19a9333b607147685ceb4443d8cbc4a5fbf1d63)

![{\displaystyle \;r=2^{-{\frac {1}{3}}}={\tfrac {1}{\sqrt[{3}]{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/791b4a671b22184f21151cb35ed313e8b4ffe66d)

![{\displaystyle {\sqrt[{3}]{2}}:1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/193ee1e945ddc2f88540ea95302d33a4d7a043b8)







![{\displaystyle {\overline {CA'}}:{\overline {A'B}}={\sqrt[{3}]{2}}:1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2963c8925ce6f96314a7901bf8c5124e62b5e6c7)




![{\displaystyle a_{1}\cdot {\sqrt[{3}]{2}}=a_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ff36d383312ae824aa70c55d5272377b40ec634)

![{\displaystyle {\overline {CA'}}:{\overline {A'B}}={\sqrt[{3}]{2}}:1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f180e3d1b26c291b2242ee73651335c946664be)







































![{\displaystyle {\begin{alignedat}{2}{\text{konstruierte Länge }}\qquad x_{3}&=&&1{,}259933493\dots \\-{\text{Sollwert }}\;\;-{\sqrt[{3}]{2}}&=-&&1{,}259921049\dots \\\hline {\text{absoluter Fehler }}\;\qquad F&=&&0{,}000012443\dots \;[\mathrm {LE} ]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f94cac3983dd0902a0f47221295e65fefb65d8d)




