Torus


Ein Torus (Plural Tori, von lateinisch torus)[1][2] ist ein mathematisches Objekt aus der Geometrie und der Topologie. Er ist eine wulstartig geformte Fläche mit einem Loch, ähnlich der Gestalt eines Rettungsrings, Fahrradschlauchs oder Donuts.
Beispiele für im dreidimensionalen Raum eingebettete Tori sind die Rotationstori. Rotationstori sind Rotationsflächen, die man erhält, indem man einen Kreis um eine Achse rotieren lässt, die in der Kreisebene liegt und den Kreis nicht schneidet. Falls man nicht nur die Kreislinie, sondern die gesamte Kreisfläche rotieren lässt, erhält man einen Volltorus.
Anders ausgedrückt wird ein Rotationstorus aus derjenigen Menge an Punkten gebildet, die von einer Kreislinie mit Radius den festen Abstand mit haben.

Ein Torus kann auch durch Identifizieren der Seiten eines Parallelogramms konstruiert werden. Dabei wird die rechte Kante des Parallelogramms mit seiner linken Kante und die obere mit der unteren Kante verheftet. Diese Topologie benutzen auch viele Computerspiele: Verlässt ein Spielobjekt auf einer Seite das Spielfeld, so taucht es auf der gegenüberliegenden Seite wieder auf.
Beide Konstruktionen sind Spezialfälle der allgemeinen mathematischen Definition, die einen Torus als das topologische Produkt zweier Kreise definiert. Dieser Begriff spielt in zahlreichen Gebieten der Mathematik eine Rolle, neben Topologie und Differentialgeometrie ist er unter anderem in der Fourier-Analysis, der Theorie dynamischer Systeme (invariante Tori in der Himmelsmechanik), der Funktionentheorie und der Theorie elliptischer Kurven von Bedeutung.
Rotationstori liefern eine konkrete rotationssymmetrische Realisierung dieser Fläche im dreidimensionalen euklidischen Raum. Von besonderer Wichtigkeit für viele Anwendungen in theoretischer Mathematik und Physik sind sogenannte flache Tori und ihre Einbettung in den vierdimensionalen Raum. Diese haben die Krümmung null und die maximal mögliche Symmetrie.
Der Torus ist eine zweidimensionale Fläche. Allgemeiner betrachtet man in der Mathematik auch den -Torus, eine den zweidimensionalen Torus verallgemeinernde -dimensionale Mannigfaltigkeit. Davon abweichend finden sich in der deutschsprachigen Literatur gelegentlich auch die Bezeichnungen Doppeltorus, Tripeltorus etc. für Flächen mit zwei, drei und mehr Löchern.
Volumen[Bearbeiten | Quelltext bearbeiten]
Das Volumen des Volltorus, der vom Torus ummantelt wird, lässt sich als Volumenintegral über die Jacobi-Determinante (die Determinante der Funktionalmatrix) berechnen. Die Jacobi-Matrix zur Parametrisierung des Torus lässt sich wie folgt angeben:
Daraus folgt:
Die Funktionaldeterminante ist hier also gleich der Norm des Flächennormalenvektors.
Man erhält also für das Volumen des Volltorus .
Die Formel für das Volumen lässt sich so interpretieren, dass die Kreisfläche mit dem Umfang multipliziert wird (siehe Zweite Guldinsche Regel). Dies kann man zum Verständnis in Analogie zum Zylindervolumen setzen. Mit dem Flächeninhalt der Oberfläche verhält es sich genauso, hier werden die Umfänge und miteinander multipliziert (siehe Erste Guldinsche Regel). Dies steht ebenfalls in Analogie zur Zylinderoberfläche .
Betrachtet man nur den inneren Teil des Torus, der von der -Achse einen Abstand kleiner gleich hat, ergibt sich das Volumen
Der äußere Teil des Torus, der von der -Achse einen Abstand größer gleich hat, hat das Volumen
Oberfläche[Bearbeiten | Quelltext bearbeiten]
Die Oberfläche des Torus mit der obigen Parameterdarstellung ist
Diese Formel lässt sich entweder mit der Ersten Guldinschen Regel herleiten aus
oder mit Hilfe des Oberflächenintegrals
berechnen. Dabei ist das Oberflächenelement des Torus in der obigen Parameterdarstellung.
Der Torus berandet einen 3-dimensionalen Volltorus. Das Volumen des Volltorus beträgt (siehe Zweiten Guldinschen Regel).
Betrachtet man nur den inneren Teil des Torus, der von der -Achse einen Abstand kleiner gleich hat, ergibt sich die Oberfläche
Der äußere Teil des Torus, der von der -Achse einen Abstand größer gleich hat, hat die Oberfläche
Torus als Rotationsfläche[Bearbeiten | Quelltext bearbeiten]


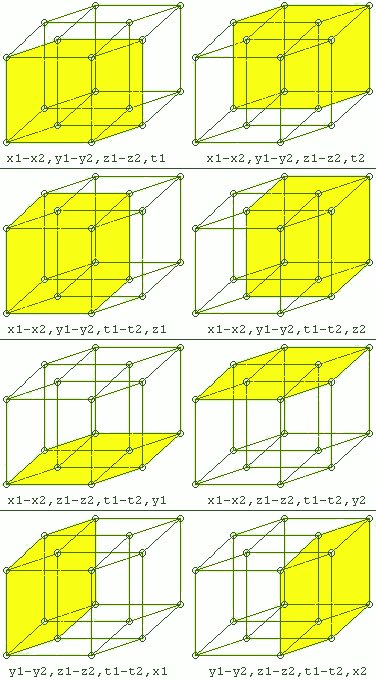
Ein Rotationstorus ist eine Rotationsfläche, die durch Rotation eines Kreises um eine in der Kreisebene liegende und den Kreis nicht schneidende Rotationsachse erzeugt wird.[3][4][5] Ein Rotationstorus kann als Menge der Punkte beschrieben werden, die von einer Kreislinie mit Radius den festen Abstand haben, wobei ist. In kartesischen Koordinaten mit der -Achse als Rotationsachse und den Mittelpunkten des rotierenden Kreises in der -Ebene wird er durch die Gleichung:
beschrieben. Durch Beseitigen der Wurzel ergibt sich die Gleichung 4. Grades
Man kann in der Torusoberfläche eine toroidale Koordinate und eine dazu senkrechte poloidale Koordinate einführen. Man denkt sich den Torus als durch einen Kreis entstanden, der um eine in der Kreisebene liegende Achse rotiert wird. Den Radius des ursprünglichen Kreises nennen wir , dieser Kreis bildet auch gleichzeitig eine Koordinatenlinie von . Den Abstand des Kreismittelpunkts von der Achse nennen wir die Koordinatenlinien von sind Kreise um die Drehachse. Beide Koordinaten sind Winkel und laufen von bis .
Parametrisierung[Bearbeiten | Quelltext bearbeiten]
Die Umrechnung von Toruskoordinaten in kartesische Koordinaten erfolgt so:
Toruskoordinaten sind in der Kernfusionstechnologie von Bedeutung, siehe Kernfusionsreaktor.
Ebene Schnitte[Bearbeiten | Quelltext bearbeiten]
- Schnitte mit Ebenen, die die Rotationsachse enthalten, sind Kreispaare.
- Schnitte mit Ebenen, die zur Rotationsachse senkrecht sind, sind Kreispaare oder ein Kreis oder leer.
- Eine zur Rotationsachse parallele Ebene schneidet aus einem Torus eine spirische Kurve aus. In Sonderfällen kann dies eine Cassinische Kurve sein.
- Eine geneigte Ebene, die zwei Erzeugerkreise berührt, schneidet Villarceau-Kreise aus.
Tori in der Darstellenden Geometrie[Bearbeiten | Quelltext bearbeiten]
In der Darstellenden Geometrie verwendet man Teile eines Torus zur Konstruktion von Übergangsflächen zwischen Zylindern. Die Darstellung eines Torus durch seinen Umriss findet man in Umrisskonstruktionen.
Allgemeine Definition[Bearbeiten | Quelltext bearbeiten]

Mit werde der Kreis (die 1-Sphäre) bezeichnet. Der -Torus ist dann definiert durch
- ,
wobei das Produkt topologischer Räume ist. Die im vorhergehenden Abschnitt beschriebene Rotationsfläche ist ein 2-Torus. Der 2-Torus wird meist einfach Torus genannt.[6]
Topologische Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Struktur einer Mannigfaltigkeit[Bearbeiten | Quelltext bearbeiten]
Der -Torus ist eine topologische Mannigfaltigkeit. Dies folgt aus der Tatsache, dass der -Torus das topologische Produkt aus 1-Sphären ist und die 1-Sphäre selbst eine topologische Mannigfaltigkeit ist. Die 1-Sphäre ist zusätzlich auch eine differenzierbare Mannigfaltigkeit und, da das Produkt differenzierbarer Mannigfaltigkeiten wieder eine differenzierbare Mannigfaltigkeit ergibt, ist der -Torus ebenfalls eine differenzierbare Mannigfaltigkeit.[7] Die Dimension von ist gleich .
Topologische Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Ebenfalls direkt aus der Definition folgt, dass der -Torus kompakt ist. Außerdem ist er wegzusammenhängend. Im Gegensatz zur -Sphäre ist der -Torus für nicht einfach zusammenhängend.
Die Abbildung , definiert durch , ist die universelle Überlagerung des -Torus.[8]
Lie-Gruppe[Bearbeiten | Quelltext bearbeiten]
Die 1-Sphäre, aufgefasst als Kreisgruppe, ist außerdem eine Lie-Gruppe. Da das Produkt mehrerer Lie-Gruppen mit der komponentenweisen Multiplikation wieder eine Lie-Gruppe ist, ist auch der -Torus eine Lie-Gruppe.[9]
Eingebettete Tori[Bearbeiten | Quelltext bearbeiten]
Flache Tori[Bearbeiten | Quelltext bearbeiten]

Da die Kreislinie offensichtlich in den eingebettet werden kann, kann der -Torus als Teilmenge des euklidischen Raums aufgefasst werden. Man betrachtet auf die riemannsche Metrik , die durch die euklidische Metrik des Raums auf dem -Torus induziert wird. Diese Metrik ist flach, das heißt, der -Torus ist lokal isometrisch zu einer Umgebung des .[10] Insbesondere ist daher seine Schnittkrümmung überall konstant null. Da der -Torus kompakt und somit auch vollständig ist, ist er eine flache Mannigfaltigkeit. Man spricht daher auch von einem flachen -Torus. Ein flacher 2-Torus kann nicht längentreu auf einen Rotationstorus im abgebildet werden, denn die Schnittkrümmung des Rotationstorus ist nicht überall null wie beim flachen 2-Torus.
Es gibt neben der oben beschriebenen noch weitere flache Metriken auf dem Torus. Flache 2-Tori können beschrieben werden durch ein Parallelogramm, dessen gegenüberliegende Seiten zusammengeklebt werden. Äquivalent dazu können flache Tori als topologische Faktorgruppen für zwei linear unabhängige Vektoren beschrieben werden. Im Spezialfall und erhält man den Quotienten .
Elliptische Kurven über den komplexen Zahlen lassen sich mittels der Weierstraßschen Parametrisierung als für ein Gitter darstellen und sind dadurch (mit einer translationsinvarianten Metrik) Beispiele für flache Tori. Der Modulraum der elliptischen Kurven oder äquivalent der flachen 2-Tori ist die sogenannte Modulkurve.
Tori im dreidimensionalen Raum[Bearbeiten | Quelltext bearbeiten]
Eine 2-mal differenzierbare Einbettung des Torus in den dreidimensionalen Raum kann nicht flach sein, weil die lokalen Extrema Punkte positiver Krümmung sein müssen. Nach dem Einbettungssatz von Nash gibt es jedoch fraktale (nur 1-mal differenzierbare) Einbettungen des flachen Torus in den dreidimensionalen Raum. Diese können auch numerisch konstruiert werden.[11][12]
Ein Rotationstorus ist ein im eingebetteter 2-Torus, der als Menge der Punkte beschrieben werden kann, die von einer Kreislinie mit Radius den festen Abstand haben, wobei ist.
Clifford-Tori[Bearbeiten | Quelltext bearbeiten]
Ein Clifford-Torus ist ein spezieller in eingebetteter Torus. Nach der Identifizierung und lässt sich der Standard-Cliffordtorus beschreiben als
- .
Weiters werden die Bilder von unter Isometrien der Standard-Metrik als Clifford-Tori bezeichnet.
Mittels stereographischer Projektion kann man Clifford-Tori auch als in den eingebettete Tori auffassen.
Ein Clifford-Torus ist eine Minimalfläche bzgl. der Standardmetrik auf der . Die von Brendle bewiesene Lawson-Vermutung besagt, dass jeder als Minimalfläche in die eingebettete Torus ein Clifford-Torus ist.
Konstruktion aus einem Quadrat oder Würfel[Bearbeiten | Quelltext bearbeiten]
Konstruktion zweidimensionaler Tori aus einem Quadrat oder Parallelogramm[Bearbeiten | Quelltext bearbeiten]


Im Gegensatz zur Oberfläche einer Kugel kann der Torus ohne Singularitäten auf einer ebenen, rechteckigen Fläche abgebildet werden.
Dabei wird die rechte Kante des Rechtecks oder Quadrats mit seiner linken Kante verheftet und seine untere Kante wird mit seiner oberen Kante verheftet. Diese Konstruktion funktioniert auch mit einem beliebigen Parallelogramm. Diese Topologie besitzen auch viele Computerspiele, zum Beispiel Asteroids oder Pac-Man: Verlässt ein Spielobjekt auf einer Seite das Spielfeld, so taucht es auf der gegenüberliegenden Seite wieder auf.
Konstruktion höherdimensionaler Tori aus einem Würfel oder Parallelepiped[Bearbeiten | Quelltext bearbeiten]
Beim dreidimensionalen Torus oder 3-Torus handelt es sich um einen Quader oder Würfel, dessen sechs gegenüberliegende Flächen paarweise miteinander verheftet sind.
Beim vierdimensionalen Torus oder 4-Torus handelt es sich um einen Tesserakt, dessen acht gegenüberliegende Würfel paarweise miteinander verheftet sind.
Allgemein ist der -dimensionale Torus ein -dimensionaler Würfel , dessen gegenüberliegende -Hyperwürfel paarweise miteinander identifiziert sind. Man kann ihn auch als darstellen.
Auch hier kann man statt eines -dimensionalen Würfels ein beliebiges -dimensionales Parallelepiped verwenden, um durch Identifizieren der Seiten einen -dimensionalen Torus zu konstruieren.
Sieben-Farben-Satz[Bearbeiten | Quelltext bearbeiten]
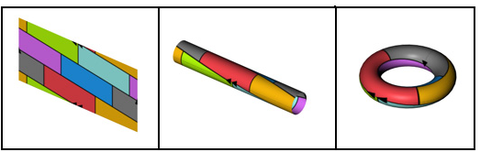
Der Sieben-Farben-Satz für den Torus besagt, dass 7 Farben immer ausreichen, eine beliebige Landkarte auf der Oberfläche eines Torus so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen.
Das bedeutet, dass jeder Graph, der in den Torus eingebettet werden kann, eine chromatische Zahl von höchstens 7 hat (siehe Knotenfärbung). Weil der vollständige Graph in den Torus eingebettet werden kann, ist die chromatische Zahl gleich 7.[13][14]
In der Ebene oder auf einer Kugeloberfläche reichen weniger Farben. Der Vier-Farben-Satz besagt, dass vier Farben immer ausreichen, eine beliebige Landkarte in der euklidischen Ebene so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen.[15][16]
Algebraischer Torus[Bearbeiten | Quelltext bearbeiten]
In der Theorie algebraischer Gruppen wird Torus in einem anderen Sinn verwendet. Dort ist damit eine Gruppe gemeint, die isomorph zu einem endlichen Produkt von Kopien der multiplikativen Gruppe eines Körpers ist. Zur Abgrenzung spricht man dann von einem algebraischen Torus im Gegensatz zu einem topologischen Torus.
So ist zum Beispiel in der torischen Geometrie, dem Studium torischer Varietäten, ein Torus üblicherweise ein algebraischer Torus.[17]
Anwendungsbeispiele[Bearbeiten | Quelltext bearbeiten]

- Ein Rettungsring mit dem Außendurchmesser 76 Zentimeter und dem Innendurchmesser 44 Zentimeter hat die Form eines Torus. Er hat also den festen Abstand von einer Kreislinie mit dem Radius .
- Daraus ergeben sich das Volumen und die Oberfläche:
- Volumen:
- Oberfläche:
- Horntorus:[18] Für die Würfelverdoppelung fand Archytas von Tarent eine nach ihm benannte Kurve. Dazu verwendete er neben einem halben Zylinder und einem Kegelausschnitt auch einen Horntorus. Darin ist der Abstand des Kreismittelpunkts von der Achse (siehe Abschnitt Torus als Rotationsfläche) gleich dem Radius des ursprünglichen Kreises.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Punktierter Torus
- Torusknoten
- Stanford-Torus
- Torus-Antenne
- Spindeltorus
- Dupinsche Zyklide
- Spirische Kurve
Literatur[Bearbeiten | Quelltext bearbeiten]
- Marcel Berger: Geometry I. Translated from the 1977 French original by M. Cole and S. Levy. Universitext. Springer-Verlag, Berlin 2009, ISBN 978-3-540-11658-5.
- Anatole Katok, Vaughn Climenhaga: Lectures on surfaces. (Almost) everything you wanted to know about them. Student Mathematical Library, 46. American Mathematical Society, Providence, RI; Mathematics Advanced Study Semesters, University Park, PA 2008, ISBN 978-0-8218-4679-7.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Torus. In: MathWorld (englisch).
- Mathcurve: Torus
- Mathematische Basteleien: Torus
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Karl Ernst Georges: torus. [1]. In: Ausführliches lateinisch-deutsches Handwörterbuch. 8., verbesserte und vermehrte Auflage. Band 2. Hahnsche Buchhandlung, Hannover 1918, Sp. 3158–3159 (Digitalisat. zeno.org).
- ↑ Es gibt noch eine Reihe weiterer heute nicht mehr gebräuchlicher historischer Verwendungen des Begriffs Torus: Torus. In: Herders Conversations-Lexikon. 1. Auflage. Band 5. Herder, Freiburg im Breisgau 1857, S. 500 (Digitalisat. zeno.org). Torus. In: Heinrich August Pierer, Julius Löbe (Hrsg.): Universal-Lexikon der Gegenwart und Vergangenheit. 4. Auflage. Band 17: Stückgießerei–Türkische Regenkugel. Altenburg 1863, S. 707 (Digitalisat. zeno.org). Torus. In: Meyers Großes Konversations-Lexikon. 6. Auflage. Band 19: Sternberg–Vector. Bibliographisches Institut, Leipzig / Wien 1909, S. 631 (Digitalisat. zeno.org). Torus. In: Brockhaus’ Kleines Konversations-Lexikon. 5. Auflage. Band 2. Brockhaus, Leipzig 1911, S. 851 (Digitalisat. zeno.org). Torus. In: Encyclopædia Britannica. 11. Auflage. Band 27: Tonalite – Vesuvius. London 1911, S. 79 (englisch, Volltext [Wikisource]).
- ↑ Ilja N. Bronstein, Konstantin A. Semendjajew: Taschenbuch der Mathematik. Harri Deutsch Verlag, 1983, ISBN 3-87144-492-8, S. 253.
- ↑ Ulrich Graf, Martin Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S. 202, 209.
- ↑ C. Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X, S. 123, 129.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218.) Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 8.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218.) Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 21.
- ↑ Tammo tom Dieck: Topologie. de Gruyter, Berlin 2000, ISBN 3-11-016236-9, S. 52.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218.) Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 39.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218.) Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 289.
- ↑ V. Borrelli, S. Jabrane, F. Lazarus, B. Thibert: Flat tori in three-dimensional space and convex integration. ( vom 1. Juli 2012 im Internet Archive; PDF) In: Proc. Natl. Acad. Sci. USA, 2012, 109, no. 19, S. 7218–7223; abgerufen am 7. Juli 2022.
- ↑ Mathématiques: première image d’un tore plat en 3D. CNRS, Pressemitteilung, 20. April 2012, abgerufen am 7. Juli 2022.
- ↑ Eric W. Weisstein: Torus Coloring. In: MathWorld (englisch).
- ↑ Chelsey Poettker: Topology and the Four Color Theorem. (PDF; 0,4 MB) Southern Illinois University Edwardsville, 4. Mai 2010; abgerufen am 7. Juli 2022.
- ↑ Eric W. Weisstein: Four-Color Theorem. In: MathWorld (englisch).
- ↑ Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas, Georgia Institute of Technology: The Four Color Theorem. 13. November 1995, abgerufen am 7. Juli 2022.
- ↑ Oda: Lectures on Torus Embeddings and Applications. 1978, 1.1 Algebraic tori.
- ↑ Eric W. Weisstein: Horn Torus. In: MathWorld (englisch).




























































![{\displaystyle [0,1]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40160923273b7109968df994dca832b91d957bf2)