„Kreiseltheorie“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
K Rechtschreibung |
Überarbeitung, weniger Formeln, Links auf neue Artikel, Redundanzen verringert |
||
| Zeile 1: | Zeile 1: | ||
Die '''Kreiseltheorie''' beschäftigt sich mit [[Rotation (Physik)|rotierenden]] Körpern, bei denen [[Translation (Physik)|translatorische]] |
Die '''Kreiseltheorie''' beschäftigt sich mit [[Rotation (Physik)|rotierenden]] Körpern, bei denen [[Translation (Physik)|translatorische Bewegunge]]n und [[Verformung]]en von untergeordneter Bedeutung sind.<ref>Grammel (1920), S. 2, Grammel (1950), S. 3.</ref> |
||
Körper, auf die diese Beschreibung zutrifft, werden in der Theorie zusammenfassend als [[Kreisel]] bezeichnet und beinhalten so verschiedene Objekte wie [[Spielkreisel]], [[Langgeschoss]]e oder die [[Erdrotation|Erde]]. Die Kreiselbewegungen sind für Mathematik, Physik und Ingenieurwesen – somit für Theorie und Praxis – gleichermaßen attraktiv. Ziel der Theorie ist es, Anwendungen auf eine sichere Grundlage zu stellen<ref>Grammel (1920), S. V, Grammel (1950), S. III, Magnus (1971), S. 1.</ref>. |
|||
Die Kreiseltheorie definiert Eigenschaften von Kreiseln ([[Massenmittelpunkt]], [[Hauptträgheitsachse]]n, …), deren Kinematik ([[Winkelgeschwindigkeit]], [[Euler-Winkel]], …) und [[Kinetik (Technische Mechanik)|Kinetik]] ([[Drehimpuls]], [[Eulersche Gleichungen (Kreiseltheorie)|Euler’sche Kreiselgleichungen]], …), leitet, auch mit dem [[Lagrange-Formalismus]], [[Bewegungsfunktion]]en der Kreisel ab und gibt Methoden ([[Poinsotsche Konstruktion]], [[Phasenraum]]­portraits, …), diese anschaulich darzustellen. |
|||
[[Leonhard Euler]] begründete die (analytische) Kreiseltheorie mit den nach ihm benannten Kreiselgleichungen, die die [[Winkelbeschleunigung]]en mit den angreifenden [[Drehmoment]]en |
[[Leonhard Euler]] begründete 1750 die (analytische) Kreiseltheorie mit den nach ihm benannten [[Eulersche Gleichungen (Kreiseltheorie)|Kreiselgleichungen]], die im körperfesten [[Bezugssystem]] die [[Winkelbeschleunigung]]en mit den angreifenden [[Drehmoment]]en verbinden. Darauf aufbauend definiert die Kreiseltheorie Eigenschaften von Kreiseln ([[Massenmittelpunkt]], [[Hauptträgheitsachse|Hauptachsen]], …), deren Kinematik ([[Euler-Winkel]], [[Winkelgeschwindigkeit]], …) und [[Kinetik (Technische Mechanik)|Kinetik]] ([[Trägheitsellipsoid]], [[Euler-Poisson-Gleichungen]], …), leitet, auch mit dem [[Lagrange-Formalismus]], [[Bewegungsfunktion]]en der Kreisel ab und gibt Methoden ([[Poinsotsche Konstruktion]], [[Phasenraum]]­portraits, …), diese anschaulich darzustellen. |
||
Anwendungen findet die Kreiseltheorie in der Eisenbahntechnik ([[Sinuslauf]]), der |
Anwendungen findet die Kreiseltheorie in der Eisenbahntechnik ([[Sinuslauf]]), der [[Drallstabilisierung]] von Schiffen ([[Schiffskreisel]]), [[Stabilisierung (Raumfahrt)|Raumflugkörpern]] und [[Trägheitsnavigationssystem]]en sowie in der [[Astronomie]] und [[Ballistik]]. |
||
== Geschichte == |
== Geschichte == |
||
Leonhard Euler entwickelte 1736 eine Theorie der [[Präzession]]<ref name="Darmstaedter"/> und 1750 die Kreiselgleichungen<ref name="Truesdell"/>, die er 1758 für den kräftefreien [[Euler-Kreisel]] lösen oder zumindest auf [[Elliptisches Integral| elliptische Integrale]] zurückführen konnte<ref name="euler"/>. [[Joseph-Louis Lagrange]] leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den [[Lagrange-Kreisel|schweren symmetrischen Kreisel mit Fixpunkt]]<ref name="lagrange"/>. [[Carl Gustav Jacob Jacobi]] veröffentlichte 1829 die Theorie der [[Jacobische elliptische Funktion| elliptischen-Funktionen]] und der [[Theta-Funktion]]en, mit denen sich die Kreiselgleichungen lösen lassen. Das hat Jacobi am Euler-Kreisel demonstriert und er empfahl 1849 mehrfach, das Problem mit diesen Funktionen anzugehen<ref>Tuschmann und Hawig (1993), S. 123.</ref>. Zwischenzeitlich veröffentlichte [[Siméon Denis Poisson]] 1838 seine kinematischen Gleichungen<ref name="poisson">{{Literatur |
|||
Bis zu Eulers bahnbrechenden Arbeiten sind folgende Beiträge zu erwähnen: |
|||
| Autor=[[Siméon Denis Poisson]] |
|||
| Titel=Traité de Méchanique |
|||
| Band=1 bis 6 |
|||
| Auflage=3 |
|||
| Verlag=J. G. Garnier |
|||
| Ort=Brüssel |
|||
| Jahr=1838 |
|||
| Sprache=fr |
|||
| Online=https://archive.org/details/bub_gb_AOnpaXuttr0C |
|||
| Zugriff=2019-11-03}}</ref>, die die Kreiselgleichungen zu den [[Euler-Poisson-Gleichungen]] vervollständigen. |
|||
Trotz des vielversprechenden Ansatzes mit Theta-Funktionen und Preisausschreiben der [[Königlich Preußische Akademie der Wissenschaften zu Berlin| preußischen]] und [[Russische Akademie der Wissenschaften| russischen Akademie der Wissenschaften]] in den 1850er Jahren erwies sich die „mathematische [[Nixe]]“, wie das „Kreiselproblem“ in Deutschland mittlerweile aufgrund seiner Attraktivität und Unnahbarkeit tituliert wurde, als äußerst unzugänglich<ref>Tuschmann und Hawig (1993), S. 123., Audin (2008), S. 91.</ref>. [[Sofia Kowalewskaja]] entdeckte 1888 den letzten durch Theta-Funktionen lösbaren Fall, den schweren, symmetrischen, inhomogenen [[Kowalewskaja-Kreisel]], womit die analytische Kreiseltheorie zu einem gewissen Abschluss kam<ref>Tuschmann und Hawig (1993), S. 119.</ref>. So sind die Standardwerke von [[Felix Klein| Klein]] und [[Arnold Sommerfeld| Sommerfeld]] (entstanden 1896-1910), [[Richard Grammel]] (1920, 1950) oder [[Kurt Magnus (Ingenieur)|Kurt Magnus]] (1971) noch zu Beginn des 21. Jahrhunderts benutzbar. Ein Beleg dafür ist, dass ersteres Werk noch 100 Jahre nach seinem Erscheinen ins englische übersetzt wurde.<ref>siehe Literatur und {{Literatur |
|||
* Archimedes gab Grundsätze über den Schwerpunkt mehrerer Größen an und formulierte Bedingungen für das statische Momentengleichgewicht<ref group="L" name="heiberg" />. |
|||
| Autor=[[Felix Klein| F. Klein]], [[Arnold Sommerfeld| A. Sommerfeld]] |
|||
* [[Johannes Kepler]] entdeckte 1609 die ersten beiden seiner drei [[Keplersche Gesetze|Kepler’schen Gesetze]], von denen das zweite eine Konsequenz der [[Drehimpuls]]­erhaltung ist. |
|||
| Titel=The Theory of the Top. Volume I |
|||
* [[Jakob I Bernoulli]] wandte 1703 den Drallsatz an – ohne ihn jedoch explizit zu formulieren – um das Oszillationszentrum eines Pendels zu finden, was er bereits auch in einem ersten, etwas unrichtigen Versuch 1686 tat.<ref group="L" name="truesdell" /> |
|||
| TitelErg=Introduction to the Kinematics and Kinetics of the Top |
|||
* [[Isaac Newton]] veröffentlichte 1687 seine [[Philosophiae Naturalis Principia Mathematica|Prinzipia]] mit seinen [[Newtonsche Gesetze|Newton’schen Gesetzen]], insbesondere formulierte er die Impulsbilanz ''Kraft gleich Masse mal Beschleunigung''. |
|||
| Originaltitel=Über die Theorie des Kreisels |
|||
| Sprache=en |
|||
| Übersetzer=R. J. Nagem, G. Sandri |
|||
| Band=Volume I |
|||
| Verlag=Birkhäuser |
|||
| Ort=Basel, Boston |
|||
| Datum=2008 |
|||
| Seiten=vii ff. |
|||
| ISBN=978-0-8176-4720-9 |
|||
| DOI=10.1007/978-0-8176-4721-6 |
|||
| Online=https://www.springer.com/gp/book/9780817647209 |
|||
| Kommentar=Das Vorwort des Übersetzers mit historischem Abriss gibt es [https://www.springer.com/cda/content/document/cda_downloaddocument/9780817647209-p1.pdf hier online als pdf-Datei]. |
|||
}}</ref> |
|||
[[Alexander Michailowitsch Ljapunow|A. M. Ljapunow]] bewies 1894, dass die drei Fälle von Euler, Lagrange und Kowalewskaja die einzigen sind, in denen die Lösung der Euler-Poisson-Gleichungen bei beliebigen Anfangsbedingungen eine eindeutige Funktion der Zeit ist, und É. Husson zeigte 1905<ref name="husson"/>, dass diese Kreisel auch die einzigen mit algebraischen Integralen lösbaren Fälle sind. Somit gelingt die Lösung mittels algebraischer Integrale nur in den Fällen, wo die Bewegung eine eindeutige Funktion der Zeit ist<ref>Leimanis (1965), S. 53 ff.</ref>. Darüber hinaus können nur spezielle Bewegungen integrabel sein. Um 1900 haben Mathematiker viele neue integrierbare Spezialfälle gefunden<ref>Magnus (1971), S. 129.</ref>, aber die Frage nach der Lösbarkeit der großen Mehrheit der Kreiselbewegungen bleibt bis ins 21. Jahrhundert hinein offen.<ref name="richter2525">Gashenenko und Richter (2003), S. 2525.</ref> |
|||
Leonhard Euler entwickelte 1736 eine Theorie der [[Präzession]] und 1750 seine Kreiselgleichungen und konnte auch schon Lösungen für den kräftefreien ''Euler-Kreisel'' angeben<ref group="L" name="kowalewskaja" />. [[Joseph-Louis Lagrange]] leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den schweren [[Symmetrischer Kreisel|symmetrischen Kreisel]]<ref group="L" name="lagrange" />. [[Carl Gustav Jacob Jacobi]] veröffentlichte 1829 seine Theorie der [[Jacobische elliptische Funktion| Jacobi'schen elliptischen Funktionen]] und der [[Theta-Funktion| Theta-Funktionen]], mit denen sich die Kreiselgleichungen lösen lassen. [[Sofia Kowalewskaja]] entdeckte 1888 den letzten durch Theta-Funktionen lösbaren Fall, den schweren, symmetrischen, inhomogenen [[Kowalewskaja-Kreisel]], womit die analytische Kreiseltheorie zu einem gewissen Abschluss kam. Édouard Husson zeigte 1905 in seiner Dissertation, dass der Euler-, Lagrange- und Kowalewskaja-Kreisel die einzigen mit algebraischen Integralen lösbaren Fälle der Kreiselgleichungen sind<ref group="L" name="husson" />. Darüber hinaus können nur spezielle Bewegungen integrabel sein. |
|||
Durch die Raumfahrt kamen neue Problemstellungen hinzu, wie beispielsweise |
Wenngleich sich die klassische Kreiseltheorie überwiegend mit dem starren Körper mit Fixpunkt befasste, so wurden doch auch kreiselähnliche Erscheinungen an rotierenden Ketten, verformbaren Körpern – insbesondere der Erde – oder Flüssigkeiten untersucht. Durch die Raumfahrt kamen neue Problemstellungen hinzu<ref name="magnus1963"/>, wie beispielsweise |
||
* die |
* die Selbsterregung (im körperfesten System aufgebrachte Momente) zwecks Stabilisierung und Lageregelung, siehe [[Stabilisierung (Raumfahrt)]], |
||
* die Bewegungen von Körpern mit veränderlichen Massen, |
* die Bewegungen von Körpern mit veränderlichen Massen, |
||
* die Bewegungen [[starrer Körper]] mit Flüssigkeitsfüllung, |
* die Bewegungen [[starrer Körper]] mit Flüssigkeitsfüllung, |
||
* die Drehbewegungen in einem zentralen Schwerefeld oder |
* die Drehbewegungen in einem zentralen Schwerefeld oder |
||
* die Beeinflussung von Translations- und Rotationsbewegungen |
* die Beeinflussung von Translations- und Rotationsbewegungen. |
||
Die meisten Kreiselbewegungen sind nicht analytisch lösbar. Die sinnfällige graphische Darstellung ihres Verhaltens wurde erst mit dem Einsatz von Computern und [[Gewöhnliche Differentialgleichung#Lösung einer gewöhnlichen Differentialgleichung mittels der numerischen Berechnung| numerischen Integrationsverfahren]] möglich und ist Anfang des 21ten Jahrhunderts Gegenstand der Forschung<ref group="L" name="interessen" /><ref group="L" name="richter2006" />. |
|||
Ab Mitte des 20. Jahrhunderts entwickelten sich die Computerhard- und -software und mit ihnen die [[numerische Simulation]] soweit, dass mit ihrer Hilfe die Bewegungsgleichungen bei beliebigen [[Anfangsbedingung]]en und jeder gewünschten Genauigkeit berechnet werden können<ref name="magnus109"/>. Die analytischen Lösungen verloren nun die früher berechtigte, zentrale Bedeutung und die nicht integrablen Fälle rückten in den Fokus. Analytische und geometrische Methoden zu ihrer Untersuchung entstanden, die auch immer wieder durch den Kowalewskaja-Kreisel motiviert waren, der die Wissenschaft das gesamte 20. Jahrhundert hindurch beschäftigte. Die Untersuchungsmethoden der integrablen Fälle wurden zu Beginn des 21. Jahrhunderts auf die nicht integrablen dynamischen Systeme übertragen.<ref>Gashenenko und Richter (2003), S. 2532 f.</ref> |
|||
== Eigenschaften der Kreisel und ihrer Bewegungen == |
== Eigenschaften der Kreisel und ihrer Bewegungen == |
||
Die Kreiseltheorie versteht unter einem Kreisel einen beliebig gestalteten [[Starrer Körper| starren Körper]], der Drehbewegungen ausführt. Dieses [[Idealisierung (Physik)| idealisierende Modell]] für wirkliche Kreisel ermöglicht deren Verhalten mit einfacheren mathematischen Hilfsmitteln zu erfassen<ref>Magnus (1971), S. 1.</ref>. Die klassische Kreiseltheorie konzentrierte sich auf den [[Schwerer Kreisel| schweren Kreisel]], der in einem [[Inertialsystem]] in einem seiner Punkte derart festgehalten wird, dass er sich um diesen Punkt noch irgendwie drehen kann<ref>Grammel (1920), S. 3, Grammel (1950), S. 2, Tuschmann und Hawig (1993), S. 121.</ref>. Diese Forderung stellt nur eine kleine Einschränkung dar, denn jede Starrkörperbewegung lässt sich in Rotation und Translation zerlegen, und sofern letztere (näherungsweise) gleichförmig ist, spielt sie für die Kreiselbewegung keine Rolle. Durch die Fixierung in einem Punkt verringert sich die Anzahl der Freiheitsgrade des Starrkörpers von sechs auf drei. |
|||
Die Geschwindigkeit der Drehbewegung ist in der Kreiseltheorie unwesentlich. Der relativ langsam umlaufende „Erdkreisel“ unterliegt den Kreiselgesetzen genauso wie ein mit 60.000 [[Drehzahl|U/min]] rotierender technischer Kreisel, allerdings vereinfachen sich die Gestzmäßigkeiten bei diesen sogenannten ''schnellen Kreiseln'' außerordentlich<ref>Magnus (1971), S. 2f.</ref>. Die Trägheitseigenschaften von Kreiseln lassen sich anschaulich durch Ellipsoide darstellen: |
|||
Jeder Starrkörper hat drei ausgezeichnete Achsen, die [[Hauptträgheitsachse]]n, die paarweise zueinander senkrecht sind oder orthogonalisierbar sind. Diese Achsen bilden eine [[Orthonormalbasis]], die kurz ''Hauptachsensystem'' genannt wird. Bezüglich dieser Achsen gleichen sich [[Fliehkraft|Fliehkräfte]] bei der Drehung genau aus und der Kreisel kann sich gleichförmig frei um sie drehen. Das Maß für den Widerstand des Kreisels gegen Bewegungsänderungen sind seine [[Trägheitsmoment]]e, die bei diesen Achsen [[Hauptträgheitsmoment]]e Θ<sub>1,2,3</sub> genannt werden. Häufig werden die Hauptträgheitsmomente Θ<sub>1,2,3</sub> auch mit ''A, B'' und ''C'' und die Hauptachsen 1, 2, 3 mit ''ξ, η'' und ''ζ'' bezeichnet. |
|||
* am [[Trägheitsellipsoid]] können die [[Trägheitsmoment]]e abgelesen werden, |
|||
* das [[Massenellipsoid]] hat dieselben Trägheitseigenschaften wie der betrachtete Körper, |
|||
Der ''unsymmetrische Kreisel'' besitzt drei ''verschiedene'' Hauptträgheitsmomente während beim ''[[Symmetrischer Kreisel|symmetrischen Kreisel]]'' zwei Hauptträgheitsmomente überein stimmen. Ist das dritte Hauptträgheitsmoment größer als die beiden anderen, dann wird der symmetrische Kreisel ''abgeplattet'' oder ''oblat'' genannt, andernfalls ''gestreckt'' oder ''prolat''. Eine anschauliche Vorstellung von der Bewegung eines symmetrischen Kreisels vermittelt der Durchstoßpunkt der [[Figurenachse]] (Symmetrieachse) durch die [[Einheitskugel]]. Dieser Durchstoßpunkt wird ''Locus'' der Figurenachse genannt<ref group="L" name="kuypers" /> ({{enS| Apex of the top}}). Von den auf den Kreisel einwirkenden äußeren Kräften ist die [[Schwerkraft]] die bei weitem wichtigste. Daher werden ''kräftefreie'' (eigentlich momentenfreie) und ''schwere Kreisel'' unterschieden, je nachdem ob der [[Gravizentrum|Schwerpunkt]] des Kreisels im Stützpunkt liegt oder nicht. Die beim symmetrischen Kreisel auf der Figurenachse und der [[Lotlinie]] senkrechte Achse wird [[Knotenlinie]] genannt. Beim ''schnellen Kreisel'' dominiert seine [[Rotationsenergie]] über andere Energieformen. |
|||
* das [[Energieellipsoid]] besteht aus allen Drehgeschwindigkeiten und |
|||
* das [[MacCullagh-Ellipsoid]] aus allen Drehimpulsen, die zur selben [[Rotationsenergie]] führen. |
|||
Die Hauptträgheitsmomente sind die [[Eigenwert]]e und die Hauptträgheitsachsen <math>\hat e_{1,2,3}</math> die dazugehörigen [[Eigenvektor]]en des [[Trägheitstensor]]s, der beim rotierenden Kreisel eine vergleichbare Rolle übernimmt wie die Masse bei der Translation. In der Kreiseltheorie wird er zumeist in der Hauptachsendarstellung verwendet und kann dort mit einer [[Diagonalmatrix]] identifiziert werden. Der Trägheitstensor bildet die Winkelgeschwindigkeit auf den Drehimpuls ab. |
|||
Die Ellipsoide rotieren mit dem Kreisel mit und die Lage der Halbachsen sowie ihre relativen Längen sind wichtige, den Kreisel charakterisierende [[physikalische Größe]]n. Denn eine Koordinate des [[Massenmittelpunkt]]s kann dazu verwendet werden, die Längen im Modell zu skalieren, und ein Hauptträgheitsmoment, um die Zeit oder Energie zu skalieren<ref name="richter2526">Gashenenko und Richter (2003), S. 2526 f.</ref>. Zwei Kreisel mit zueinander ähnlichen Ellipsoiden und vergleichbarer Lage des Massenmittelpunkts bewegen sich daher ähnlich. Das motiviert die vielen Begriffe zur Beschreibung der Massenverteilung von Kreiseln, wie [[Symmetrischer Kreisel|symmetrischer]] und [[unsymmetrischer Kreisel]], die noch prolat oder oblat bzw. lang-, mittel- oder kurzachsig sein können. |
|||
=== Drehgeschwindigkeit und Drehimpuls === |
=== Drehgeschwindigkeit und Drehimpuls === |
||
Die [[Winkelgeschwindigkeit]] lässt sich kompakt als [[Vektor]] ausdrücken: Seine Richtung definiert die [[Drehachse]] und sein Betrag die Drehgeschwindigkeit um diese Achse. Gleiches gilt für den [[Drehimpuls]], der ein Maß für den Schwung des Kreisels ist und der ebenfalls Richtung und Betrag besitzt. |
|||
{{Hauptartikel| Energieellipsoid}} |
|||
[[Datei:Energieellipsoid2d.png|mini|400px| Abb. 1: Schnitt durch ein [[Energieellipsoid]] entlang zweier Hauptachsen, mit den Hauptträgheitsmomenten θ<sub>1</sub> und θ<sub>2</sub>]] |
|||
Die [[Winkelgeschwindigkeit]] lässt sich kompakt als [[Vektor]] <math>\vec\omega</math> ausdrücken: Seine Richtung definiert die Drehachse und sein Betrag die Drehgeschwindigkeit um diese Achse. Gleiches gilt für den [[Drehimpuls]] <math>\vec L</math>, der ein Maß für den Schwung des Kreisels ist und der ebenfalls Richtung und Betrag besitzt. |
|||
Die Dynamik des Kreisels lässt sich mit dem Drehimpuls ähnlich der Dynamik des Massenpunkts formulieren<ref |
Die Dynamik des Kreisels lässt sich mit dem Drehimpuls ähnlich der Dynamik des Massenpunkts formulieren:<ref>Klein und Sommerfeld (1910), S. 762.</ref> |
||
# Der kräftefreie Kreisel bewegt sich so, dass sein Drehimpuls nach Betrag und Richtung konstant bleibt (so wie sich ein kräftefreier Massenpunkt gleichförmig bewegt). |
# Der kräftefreie Kreisel bewegt sich so, dass sein Drehimpuls nach Betrag und Richtung konstant bleibt (so wie sich ein kräftefreier Massenpunkt gleichförmig bewegt). |
||
# Unter dem Einfluss von [[Drehmoment]]en bewegt sich der Kreisel derart, dass die Änderungsgeschwindigkeit des Drehimpulsvektors nach Richtung und Betrag gleich dem angreifenden Moment ist (so wie die Beschleunigung des Massenpunkts in Richtung einer angreifenden Kraft erfolgt) |
# Unter dem Einfluss von [[Drehmoment]]en bewegt sich der Kreisel derart, dass die Änderungsgeschwindigkeit des Drehimpulsvektors nach Richtung und Betrag gleich dem angreifenden Moment ist (so wie die Beschleunigung des Massenpunkts in Richtung einer angreifenden Kraft erfolgt). |
||
Die [[Rotation (Physik)#Vergleich mit der Translationsbewegung| Analogien zwischen Rotation und Translationsbewegung]] hören jedoch dort auf, wo die typischen Kreiselbewegungen beginnen. Denn während [[Impuls (Physik)| Impuls]] und Geschwindigkeit bei der Translation immer parallel und proportional zueinander sind, trifft das auf Drehimpuls und Drehgeschwindigkeit in den kreiseltheoretisch interessanten Fällen nicht zu. Wird ein anfangs ruhender Kreisel durch einen [[Drehstoß]] um eine Achse in Drehung versetzt, muss er anschließend keineswegs um diese Achse kreisen<ref>Magnus (1971), S. 2 und S. 47, Grammel (1920), S. 43.</ref>. Bei konstantem Drehimpuls muss die Winkelgeschwindigkeit mitnichten konstant sein und umgekehrt, was der [[Dschanibekow-Effekt]] eindrücklich untermauert, siehe auch [[#Drehimpuls und Rotationsenergie von Kreiseln]]. |
|||
Wird der Drehimpuls im körperfesten Hauptachsensystem ausgedrückt, dann sind die Komponenten in Richtung der Hauptachsen mit den größten Hauptträgheitsmomenten gegenüber den entsprechenden Drehgeschwindigkeiten betont. Die Richtung des Drehimpulses liegt daher immer irgendwo zwischen der Drehachse und den Hauptachsen mit den größten Hauptträgheitsmomenten. |
|||
In Abb. 1 ist ein Schnitt durch ein [[Energieellipsoid]] zu sehen, das die Menge aller Winkelgeschwindigkeiten ist, die bei einem gegebenen Kreisel zur selben [[Rotationsenergie]] ''E''<sub>rot</sub> führen. Die Richtung des Drehimpulses steht immer senkrecht auf dem Energieellipsoid in dem Punkt, wo die aktuelle Winkelgeschwindigkeit dieses berührt. Die Länge der Halbachsen des Ellipsoids sind umgekehrt proportional zu den Hauptträgheitsmomenten: Das Hauptträgheitsmoment in horizontaler Richtung ist im Bild kleiner als das in vertikaler. Daher ist der Drehimpuls im Bild steiler ausgerichtet als die Winkelgeschwindigkeit. Nur bei Drehungen um eine der Hauptachsen sind Drehimpuls und Winkelgeschwindigkeit parallel. Liegt die Drehachse hingegen dazwischen, schließen sie einen [[Spitzer Winkel|spitzen Winkel]] ein und der ist umso spitzer, je näher die Winkelgeschwindigkeit an einer Hauptachse liegt. |
|||
=== Präzession und Nutation des symmetrischen Kreisels === |
|||
{{Hauptartikel|Symmetrischer Kreisel}} |
|||
[[Datei: Kreiselkegel.png| mini| Abb. 2: Bewegungsform eines symmetrischen, prolaten, kräftefreien Kreisels]] |
|||
Betrachtet werden freie Bewegungen, bei denen die Drehachse ihre Richtung ändern kann. |
|||
Die Bewegungen des kräftefreien Kreisels werden in der Kreiseltheorie [[Nutation (Physik)| Nutation]] genannt und die fremderregten [[Präzession]]<ref group="F">Magnus (1971), S. 119</ref><ref group="L" name="präzession" />. Allerdings sind diese Bezeichnungsweisen nicht einheitlich. Arnold<ref group="L" name="arnold" /> beispielsweise nennt beim [[Lagrange-Kreisel|schweren symmetrischen Kreisel]] die periodische Änderung der Neigung der Figurenachse gegenüber der [[Lotlinie]] Nutation und die [[azimut]]ale Drehung Präzession. |
|||
Rotiert der kräftefreie symmetrische Kreisel nicht um eine Hauptachse, dann fallen Drehimpuls und Winkelgeschwindigkeit nicht zusammen und die Figurenachse bewegt sich auf einem Kegel im Raum, siehe Abb. 2. Die Figurenachse ist körperfest. |
|||
Die Drehachse eines Kreisels ist nicht körperfest, sie kann sich also relativ zum Kreisel bewegen. Bei der Nutation des kräftefreien symmetrischen Kreisels beschreibt die Drehachse relativ zum Kreisel einen Kegel, den Gangpolkegel, mit konstantem Öffnungswinkel um die Figurenachse. Gleichzeitig überstreicht die Drehachse auch um die vom Drehimpuls gestellte ''Präzessionsachse''<ref group="F">Grammel (1920), S. 40.</ref> einen Kegel, den Rastpolkegel, ebenfalls mit konstantem Öffnungswinkel, diesmal um die Präzessionsachse. Diese ''reguläre Präzession'' kann auch beim [[Lagrange-Kreisel| schweren symmetrischen Kreisel]] als Sonderfall auftreten. |
|||
Wenn der schwere Kreisel die speziellen Bedingungen der regulären Präzession nicht erfüllt, dann beschreibt der Locus der Figurenachse eine [[zykloide]]n­ähnliche Kurve, die sich auf die Präzession auswirkt. Diese überlagerte Bewegung wird nach einem der [[Astronomie]] entlehnten Wort ebenfalls [[Nutation (Astronomie)| Nutation]] genannt<ref group="L" name="kuypers" /><ref group="L" name="autenrieth"/>. Je größer das Verhältnis zwischen Rotations- und Lageenergie des Kreisels ist, desto kleiner wird der Radius der Zykloide, und das kann so weit gehen, dass die Rollkurve mit dem Auge nicht mehr als solche wahrnehmbar ist. Die Präzession sieht dann aus wie eine reguläre Präzession, ist aber keine, und wird ''pseudoreguläre Präzession'' genannt<ref group="L" name="autenrieth"/><ref group="L" name="sommer2010" />. |
|||
=== Drallsatz === |
=== Drallsatz === |
||
{{Hauptartikel| Drallsatz}} |
{{Hauptartikel| Drallsatz}} |
||
[[Datei: tendency to equiorientational parallelism.png| mini|Abb. |
[[Datei: tendency to equiorientational parallelism.png| mini| Abb. 1: Zur Regel vom gleichsinnigen Parallelismus]] |
||
Das in der Kreiseltheorie wichtigste physikalische Gesetz ist der [[Drallsatz]], der sich beim Kreisel als ''Regel vom gleichsinnigen Parallelismus''<ref |
Das in der Kreiseltheorie wichtigste physikalische Gesetz ist der [[Drallsatz]], der sich beim Kreisel als ''Regel vom gleichsinnigen Parallelismus''<ref name="Regel vom gleichsinnigen Parallelismus">Klein und Sommerfeld (1910), S. 764.</ref> ausdrückt, siehe Abb. 1.: Greift am Kreisel ein [[Drehmoment]] ''M'' an, dann versucht der Kreisel seine Drehbewegung, ausgedrückt durch den Drehimpuls ''L'', dem Drehsinn des Moments gleichsinnig parallel auszurichten, was im Bild blau angedeutet ist. Aus diesem Grundsatz leiten sich viele Eigenschaften der Kreiselbewegungen ab. Wirkt auf den Kreisel beispielsweise eine [[Kraft]], dann ist das von ihr ausgeübte Drehmoment senkrecht zu ihr und somit weicht ein rotierender Kreisel einer Kraft immer senkrecht zu ihrer Wirkungslinie aus. Das gilt jedoch nur für den Drehimpuls und nicht notwendigerweise auch für die Drehachse oder eine [[Symmetrieachse]] des Kreisels. |
||
Der Drallsatz besagt, dass um den Drehimpuls eines Kreisels zu verändern, ein Drehmoment angreifen muss. Ohne solche Momente bleibt der Drehimpuls in Betrag und Richtung erhalten. |
Der Drallsatz besagt, dass um den Drehimpuls eines Kreisels zu verändern, ein Drehmoment angreifen muss. Ohne solche Momente bleibt der Drehimpuls in Betrag und Richtung erhalten. Aus dem Drallsatz leiten sich auch die Euler’schen Kreiselgleichungen ab, mit denen die rechnerische Behandlung der Kreiselbewegungen erfolgt. Der Drehimpuls und die Drehachse sind nur in Spezialfällen parallel. Im Allgemeinen gilt: |
||
:<math>\vec M = \dot{\vec L}</math> |
|||
Darin ist <math>\vec M</math> das am Kreisel angreifende Drehmoment, <math>\vec L</math> der [[Drehimpuls]] des Kreisels und <math>\dot{\vec L}</math> seine zeitliche Änderung. Aus dem Drallsatz leiten sich auch die Euler’schen Kreiselgleichungen ab, mit denen die genaue rechnerische Behandlung der Kreiselbewegungen erfolgt, siehe unten. Der Drehimpuls und die Drehachse sind – wie oben berichtet – nur bei Drehungen um eine der Hauptachsen parallel. In den anderen Fällen gilt: |
|||
* Bei konstantem Drehimpuls ändert sich bei freier Bewegung fortlaufend die Drehachse und der Kreisel taumelt oder „eiert“. |
* Bei konstantem Drehimpuls ändert sich bei freier Bewegung fortlaufend die Drehachse und der Kreisel taumelt oder „eiert“. |
||
* Wird die Drehachse festgehalten, dann ändert sich fortlaufend der Drehimpuls, |
* Wird die Drehachse festgehalten, dann ändert sich fortlaufend der Drehimpuls, wofür die Halterungen der Drehachse die dazu notwendigen Momente einbringen und die Kreiselwirkungen abtragen müssen. |
||
** Die Halterungen der Drehachse müssen die dazu notwendigen Momente einbringen. |
|||
** Umgekehrt werden die Halterungen durch die Reaktionsmomente belastet und müssen diese abtragen. |
|||
Integration obiger Gleichung über die Zeit liefert |
|||
:<math>\vec L=\vec L_0+\int \vec M\,\mathrm{d}t</math> |
|||
Das Integral ist der ''Drehstoß''. Bei anfänglich ruhendem Körper liefert er einen Drehungszustand, der nicht notwendigerweise parallel zur Drehachse ist, worin sich die [[Anisotropie]] des starren Körpers gegenüber Drehbewegungen ausdrückt<ref group="F">Magnus (1971), S. 47.</ref>. Der unsymmetrische Kreisel ist doppelt anisotrop, der symmetrische einfach anisotrop und nur der [[Kugelkreisel]] isotrop.<ref group="F">Grammel (1920), S. 43.</ref> |
|||
Das Moment kann in eine Komponente ''M''<sub>L</sub> parallel zum Drehimpuls ''L''<sub>0</sub> und eine Komponente ''M''<sub>P</sub> senkrecht dazu zerlegt werden. Erstere Komponente wirkt nur auf den Betrag des Drehimpulses nicht aber auf seine Richtung und letztere Komponente wirkt umgekehrt nicht auf den Betrag, sondern nur auf die Richtung. Ändert sich diese im Zeitintervall Δ''t'' um den Winkel Δ''α'', dann entsteht<ref group="F">Magnus (1971), S. 100.</ref>: |
|||
:<math>\omega_\text{P}=\lim_{\Delta t\to0}\frac{\Delta\alpha}{\Delta t}=\frac{M_\text{P}}{L_0} |
|||
\quad\text{oder}\quad |
|||
M_\text{P}=\omega_\text{P}\cdot L_0 |
|||
</math> |
|||
ein Zusammenhang, der bei der Quantifizierung der [[#Drallstabilisierung]] unten ausgenutzt wird. Eine Verallgemeinerung in drei Dimensionen erklärt die [[Lagrange-Kreisel#Pseudoreguläre Präzession| Pseudoreguläre Präzession des Lagrange-Kreisels]]. |
|||
=== Kreiselwirkung === |
=== Kreiselwirkung === |
||
{{Hauptartikel| |
{{Hauptartikel| Kreiselwirkung}} |
||
Das auffälligste Merkmal von Kreiseln ist die des gyroskopischen Effekts oder der |
Das auffälligste Merkmal von Kreiseln ist die des gyroskopischen Effekts oder der Kreiselwirkung, die sich als verblüffende Kraftäußerung bemerkbar macht, wenn man versucht, die Drehachse eines Kreisels in eine neue Lage zu bringen. Die Kreiselwirkung äußert sich dabei als Widerstand, der über das beim ruhenden Körper bekannte Maß weit hinausgehen kann<ref name="grammel3">Grammel (1920), S. 3</ref>. |
||
Die Kreiselwirkung < |
Die Kreiselwirkung versucht nach der Regel des gleichsinnigen Parallelismus die Achse der Eigendrehung in Richtung und Orientierung mit der Achse der erzwungenen Drehung zur Deckung zu bringen<ref>Grammel (1920), S. 70.</ref>. Die Kreiselwirkung ist eine [[Trägheitskraft#D’Alembertsche Trägheitskraft| d’Alembertsche Trägheitskraft]] und als solche ein einem angreifenden Moment entgegengesetzt gleichgroßes Moment: Moment und Kreiselwirkung befinden sich im [[Dynamisches Gleichgewicht (Technische Mechanik)|dynamischen Gleichgewicht]]. |
||
Die Kreiselwirkung ist gleich der Summe der im Körper durch die [[Euler-Kraft| Euler-]] und [[Zentrifugalkraft| Zentrifugalkräfte]] ausgeübten Momente, siehe [[#Euler’sche Kreiselgleichungen]]. In den Richtungen senkrecht zum angreifenden Moment neutralisieren sich die Kreiselwirkungen der Euler- und Zentrifugalkräfte und befinden sich dort untereinander im dynamischen Gleichgewicht. Die Euler-Kräfte sind Ausdruck von Winkelbeschleunigungen, die dort von den Zentrifugalkräften im Kreisel hervorgerufen werden. Umgekehrt führen die Winkelbeschleunigungen zur Änderung der Drehachse und Drehgeschwindigkeit, was die Zentrifugalkräfte beeinflusst. Auswirkung dieses dynamischen Wechselspiels ist besagtes Taumeln und „Eiern“ des kräftefreien Kreisels. Die Kreiselwirkungen werden bei [[Kurvenkreisel]]n, [[Kollermühle]]n und der Drallstabilisierung technisch ausgenutzt. |
|||
:<math>\vec K = -\vec M</math> |
|||
Moment und Kreiselwirkung befinden sich im dynamischen Gleichgewicht. Somit entspricht die Kreiselwirkung der negativen Drehimpulsänderung und ist gleich der Summe der Kreiselwirkungen der [[Euler-Kraft|Euler-]] und (fiktiven, s. u.) [[Zentrifugalkraft|Zentrifugalkräfte]] im Körper: |
|||
:<math>\vec K = \vec K_\mathrm{Euler}+\vec K_\text{Zentrifugal} = -\dot{\vec L}</math>. |
|||
In den Richtungen senkrecht zum angreifenden Moment neutralisieren sich die Kreiselwirkungen der Euler- und Zentrifugalkräfte und befinden sich dort somit untereinander im dynamischen Gleichgewicht. Die Euler-Kräfte sind Ausdruck von Winkelbeschleunigungen, die dort von den Zentrifugalkräften im Kreisel hervorgerufen werden. Umgekehrt führen die Winkelbeschleunigungen zur Änderung der Drehachse und Drehgeschwindigkeit, was die Zentrifugalkräfte beeinflusst. Folge dieses dynamischen Wechselspiels ist besagtes Taumeln und „Eiern“ des kräftefreien Kreisels. |
|||
=== Drallstabilisierung === |
=== Drallstabilisierung === |
||
{{Hauptartikel| Drallstabilisierung}} |
|||
[[Datei:sketch flywheel.png| mini| Abb. 2: Schwungrad zur Erläuterung der Drallstabilisierung]] |
|||
Eine der technisch wertvollsten Eigenschaften von Kreiseln ist die Möglichkeit, mit ihnen Körper in ihrer räumlichen Ausrichtung zu stabilisieren. Dies wird, wie schon eingangs erwähnt, bei Schiffen, Raumflugkörpern und Geschossen ausgenutzt. |
|||
Um die Drallstabilisierung zu erläutern, wird die Bewegung des Schwungrads in Abb. 2 betrachtet, wobei die [[Figurenachse]] (anfänglich in y-Richtung) frei ist, so dass sie ihre Richtung beliebig ändern kann. Auf dieses ansonsten kräftefreie Schwungrad wirke eine kurze Zeit in z-Richtung ein konstantes Moment ''M''<sub>z</sub>, das das Schwungrad in Drehung um z versetzt. Diese Drehung macht sich am ruhenden und rotierenden Schwungrad jedoch unterschiedlich bemerkbar: |
|||
[[Datei:sketch flywheel.png|mini|Abb. 4: Schwungrad zur Erläuterung der Kreiselwirkung]] |
|||
Eine der technisch wertvollsten Eigenschaften von Kreiseln ist die Möglichkeit, mit ihnen Körper in ihrer räumlichen Ausrichtung zu stabilisieren. Dies wird, wie schon eingangs erwähnt, bei Schiffen, Raumflugkörpern und Geschossen ausgenutzt. Die Drallstabilisierung basiert auf Kreiselwirkungen. |
|||
Um das zu erläutern, wird die Bewegung des Schwungrads in Abb. 4 betrachtet, wobei die Figurenachse (anfänglich in y-Richtung) frei ist, so dass sie ihre Richtung beliebig ändern kann. Auf dieses ansonsten kräftefreie Schwungrad wirke eine kurze Zeit in z-Richtung ein konstantes Moment ''M''<sub>z</sub>, das das Schwungrad in Drehung um z versetzt. Diese Drehung macht sich am ruhenden und rotierenden Schwungrad jedoch unterschiedlich bemerkbar: |
|||
# Ruht das Schwungrad, dann beginnt es durch das Moment um z zu rotieren. Nachdem das Moment aufgehört hat zu wirken, verharrt das Schwungrad in der Drehung um z, es gibt keine Kreiselwirkung und der Drehwinkel ''ψ'' der Figurenachse um z nimmt monoton zu und ist unbeschränkt. Die Winkelgeschwindigkeit und der Drehimpuls haben nur eine Komponente und die weist in z-Richtung. Der Neigungswinkel ϑ zwischen Figurenachse und Momentenachse z bleibt unverändert. |
# Ruht das Schwungrad, dann beginnt es durch das Moment um z zu rotieren. Nachdem das Moment aufgehört hat zu wirken, verharrt das Schwungrad in der Drehung um z, es gibt keine Kreiselwirkung und der Drehwinkel ''ψ'' der Figurenachse um z nimmt monoton zu und ist unbeschränkt. Die Winkelgeschwindigkeit und der Drehimpuls haben nur eine Komponente und die weist in z-Richtung. Der Neigungswinkel ϑ zwischen Figurenachse und Momentenachse z bleibt unverändert. |
||
# Rotiert das Schwungrad anfänglich hinreichend schnell um die Figurenachse, dann zeigt sich ein anderes Bild. Zwar führt das Moment auch hier zu einer linearen Zunahme des Drehimpulses in z-Richtung, aber weil sich diese |
# Rotiert das Schwungrad anfänglich hinreichend schnell um die Figurenachse, dann zeigt sich ein anderes Bild. Zwar führt das Moment auch hier zu einer linearen Zunahme des Drehimpulses in z-Richtung, aber weil sich diese Komponente zum anfänglichen (als viel größer angenommenen) Drehimpuls in y-Richtung vektoriell addiert, der Drehimpuls also weiter vor allem in y-Richtung orientiert ist, und Drehimpuls und Winkelgeschwindigkeit einen spitzen Winkel einschließen (siehe [[#Drall und Rotationsenergie von Kreiseln]]), dreht das Schwungrad weiter vor allem um die y-Achse. Dadurch bleibt der Drehwinkel ''ψ'' der Figurenachse um z beschränkt. Nach der Regel vom gleichsinnigen Parallelismus versucht der Kreisel seine Drehung dem angreifenden Moment anzugleichen, wodurch der Winkel ϑ abnimmt. |
||
Ursache für den geringen Einfluss des Moments auf die Drehung des rotierenden Schwungrads um z sind Trägheitskräfte, die |
Ursache für den geringen Einfluss des Moments auf die Drehung des rotierenden Schwungrads um z sind Trägheitskräfte, die Kreiselwirkungen aufbauen. Wird die Drehachse durch Lager irgendwie gehalten, neutralisieren sie diese Kreiselwirkungen und können die Trägheitskräfte nicht ihr Potenzial entfalten. Drallstabilisierung tritt nur bei Kreiseln auf, die ihre volle Bewegungsfreiheit in drei Drehfreiheitsgraden besitzen<ref>Klein und Sommerfeld (1910), S. 767 f.</ref>. Aber selbst dann gelingt eine Drallstabilisierung nicht immer, wie [[William Thomson, 1. Baron Kelvin]] und [[Peter Guthrie Tait]] zeigen konnten.<ref>Grammel (1950), S. 261 f.</ref> |
||
# Das kleine Moment ''M''<sub>z</sub> dreht das Schwungrad mit Drehimpuls ''L'' in y-Richtung zunächst (langsam) um die z-Achse und der Winkel ''ψ'' zur Figurenachse nimmt gemäß der Beschleunigungsgleichung <math>A\ddot\psi = M_z</math> zu. Der Beschleunigungsterm <math>A\ddot\psi</math> ist eine Kreiselwirkung in -z-Richtung, die sich aus Euler-Kräften speist. |
|||
# So bekommt die Winkelgeschwindigkeit eine kleine Komponente in z-Richtung und die Neigung ϑ der Drehachse gegenüber der Vertikalen verringert sich entsprechend <math>A\ddot\vartheta = -L\dot\psi\rightarrow\dot\vartheta = -\tfrac{L}{A}\psi</math>. Diese Winkelbeschleunigung um x zieht Euler-Kräfte nach sich, die in Summe eine Kreiselwirkung in -x-Richtung hervorbringen. |
|||
# In gleicher Weise wie das Moment ''M''<sub>z</sub> die Kreiselwirkung in -x-Richtung hervorruft, so entsteht durch letztere eine weitere Kreiselwirkung <math>L\dot\vartheta = -\tfrac{L^2}{A}\psi</math> in -z-Richtung, die der Beschleunigungsgleichung im ersten Schritt hinzu zu fügen ist: <math>A\ddot\psi = M_z-\tfrac{L^2}{A}\psi</math>. |
|||
# Ganz analog wie das Moment ''M''<sub>z</sub> eine entgegengesetzte Kreiselwirkung auslöst, besitzt auch die Kreiselwirkung in -x-Richtung eine Widersacherin in +x-Richtung, die sich aus den Zentrifugalkräften im Schwungrad speist und die ebenfalls zur Kreiselwirkung in -z-Richtung beiträgt. |
|||
=== Bewegungen von Kreiseln mit Fixpunkt === |
|||
Während sich die Kreiselwirkungen in -z-Richtung (<math>A\ddot\psi</math> und <math>\tfrac{L^2}{A}\psi</math>) genau zu ''M''<sub>z</sub> summieren, löschen sich die Kreiselwirkungen in x- und y-Richtung genau aus. Das Moment der Euler-Kräfte ist dort antiparallel zum Moment der Zentrifugalkräfte. Auf diese Weise bleiben die Drehimpulse in x- und y-Richtung gegenüber dem Anfangszustand unverändert. |
|||
[[Datei: Kreiselkegel.png| mini| Abb. 3: Bewegungsform eines symmetrischen, prolaten, kräftefreien Kreisels]] |
|||
Betrachtet werden freie Bewegungen, bei denen die Drehachse ihre Richtung ändern kann. |
|||
Die Bewegungen des kräftefreien Kreisels werden in der Kreiseltheorie [[Nutation (Physik)| Nutation]] genannt und die fremderregten [[Präzession]]<ref>Magnus (1971), S. 119</ref><ref name="präzession"/>. Allerdings sind diese Bezeichnungen nicht einheitlich. Arnold<ref name="arnold"/> beispielsweise nennt die periodische Änderung der Neigung der Figurenachse gegenüber der [[Lotlinie]] beim [[Lagrange-Kreisel]] Nutation und die [[azimut]]ale Drehung Präzession. |
|||
Die im dritten Schritt erhaltene Gleichung für die Winkelbeschleunigung <math>\ddot\psi</math> ist eine [[Schwingungsgleichung]], weswegen die Figurenachse unter dem Moment in z-Richtung eine Schwingung um z ausführt. Mit dem konstanten Drehimpuls <math>L = B\dot\varphi</math> in y-Richtung lautet die Schwingungsgleichung |
|||
Die Drehachse eines Kreisels ist nicht körperfest, sie kann sich also relativ zum Kreisel bewegen und überstreicht dabei den körperfesten Gangpolkegel oder kurz Polkegel. Gleichzeitig bewegt sich die Drehachse auch im Raum und erzeugt dadurch eine Fläche, den Rastpol- oder Spurkegel. Die Leitkurve der Kegel ist der Endpunkt des Winkelgeschwindigkeitsvektors, der teils chaotisch schwankt, nur selten einen Zustand zweimal einnimmt und beliebig geformte [[Spurkegel und Polkegel]] erzeugt. Beim Kreisel mit Fixpunkt befinden sich die Spitzen der Kegel in diesem Punkt und der Polkegel rollt [[schlupf]]­los auf dem Spurkegel ab<ref>Magnus (1971), S. 27.</ref>. Beim symmetrischen [[Euler-Kreisel]] sind die Kegel [[Kreiskegel]] und die Bewegung besonders anschaulich, siehe Bild. |
|||
:<math>\frac{M_z}{A} = \ddot\psi+\left(\frac{B}{A}\dot\varphi\right)^2\psi</math> |
|||
Der [[Euler-Kreisel|kräftefreie Kreisel]] befolgt mangels äußerer Einwirkungen den [[Energieerhaltungssatz]]. Solche Erhaltungsgrößen sind in der Kreiseltheorie von großem Interesse und werden [[#Integrale der Bewegung]] genannt. Dem [[Spielkreisel]] nahe verwandt ist der [[Lagrange-Kreisel]], an dem paradoxe Kreiselerscheinungen auffallen: |
|||
Darin ist ''φ'' der Drehwinkel um die [[Figurenachse]]. Die Eigenkreisfrequenz der Schwingung der Figurenachse um die z-Achse ist demnach proportional zum Verhältnis der Trägheitsmomente und zur Winkelgeschwindigkeit um die Figurenachse. Die Schwingungsgleichung ist eine Näherung, die nur bei kleiner Auslenkung ''ψ'' gültig ist. Aus <math>\dot\vartheta = -\tfrac{L}{A}\psi</math> kann mit ''ψ'' auch ϑ berechnet werden. |
|||
* die Präzession mit horizontaler [[Figurenachse]] und |
|||
* das Auffrichten des Kreisels entgegen der Schwerkraft. |
|||
Beim [[Kowalewskaja-Kreisel]] sind die Bewegungsfunktionen mathematisch anspruchsvoll und fast alle seine Bewegungen ändern ihr Stabilitätsverhalten wenn sie schneller oder langsamer erfolgen. Der deutsche [[Wilhelm Hess (Mathematiker)| Mathematiker Wilhelm Hess]] entdeckte 1890 das [[Hess’sches Pendel| loxodromische Pendel]], dessen Schwerpunkt sich wie bei einem [[Sphärisches Pendel| sphärischen Pendel]] unter kreiselspezifischer Schwerebeschleunigung bewegt. |
|||
Jeder Kreisel kann permanente [[Staude-Drehung]]en um eine körperfeste [[lotrecht]]e Achse ausführen. Ebenfalls sind [[pseudoreguläre Präzession]]en möglich, wenn der Drehimpuls groß und nahe einer Symmetrieachse ausgerichtet ist. Die Bewegung gleicht der [[reguläre Präzession| regulären Präzession]], bei der der Kreisel um eine raumfeste und eine andere körperfeste Achse gleichmäßig rotiert und die beiden Achsen einen gleichbleibenden Winkel einschließen. Bei der pseudoregulären Präzession treten jedoch mit dem Auge kaum wahrnehmbare, kleine, überlagernde, [[zykloide]]n­ähnliche Oszillationen der Drehachse auf, die nach einem der [[Astronomie]] entlehnten Wort ebenfalls [[Nutation (Astronomie)| Nutationen]] genannt werden<ref>Kuypers (2016), S. 215</ref><ref name="autenrieth">{{Literatur |
|||
Für die stabilisierende Kreiselwirkung ist dabei die freie Drehungsmöglichkeit der Figurenachse um die äquatorialen Achsen entscheidend. Wird die Drehachse durch Lager an die xy-Ebene gebunden, können die Momente der Trägheitskräfte nicht ihr Potenzial entfalten und es tritt keine Drallstabilisierung auf<ref group="F">Klein und Sommerfeld (1910), S. 767f</ref>. |
|||
| Autor=[[Edmund Friedrich Autenrieth| E. F. Autenrieth]], Max Ensslin |
|||
| Titel=Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure |
|||
| Verlag=Springer-Verlag |
|||
| Ort=Berlin |
|||
| Jahr=1922 |
|||
| ISBN=978-3-642-98876-9 |
|||
| Online={{Google Buch| BuchID=OTeuBgAAQBAJ| Seite=423}} |
|||
| Zugriff=2017-11-05 |
|||
}}</ref>. |
|||
Eine Zusammenstellung der wenigen Fälle, in denen bis Anfang des 21. Jahrhunderts exakte Lösungen der Bewegungsgleichungen gelungen sind, finden sich bei den [[Euler-Poisson-Gleichungen]]<ref>Magnus (1971), S. 108.</ref>. Die Energiefläche, auf der die Winkelgeschwindigkeit entlangfährt, kann bei allen Kreiseln analytisch beschrieben werden und es zeigt sich, dass die Fläche in relativen Gleichgewichten [[Bifurkation (Mathematik)|verzweigen]] kann, beispielsweise wenn der Kreisel die aufrechte Position passiert. In solchen Verzweigungspunkten ändert die Energiefläche ihre Eigenschaften ([[Topologie (Mathematik)|Topologie]]), was analytisch darstellbar und kreiseltheoretisch von Interesse ist.<ref name="richter2526"/> |
|||
== Kinematik von Kreiseln == |
== Kinematik von Kreiseln == |
||
Die Kinematik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die nicht von der Masse abhängen. |
Die Kinematik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die nicht von der Masse abhängen. |
||
=== Bezugssysteme und Euler-Winkel === |
|||
=== Eulersche Geschwindigkeitsgleichung === |
|||
{{Hauptartikel| Bezugssystem}} |
|||
Die allgemeine Bewegung starrer Körper ist durch die eulersche Geschwindigkeitsgleichung |
|||
{{Anker| eulerframe.svg}} |
|||
[[Datei:eulerframe.svg|mini|Abb. 4: Das eulersche Basissystem (grün) gibt die Achsen an, um die die Euler-Winkel ''ψ=α'', ''ϑ=β'' und ''φ=γ'' drehen.]] |
|||
In der Kreiseltheorie werden vor allem zwei Bezugssysteme verwendet: |
|||
:<math>\vec v(\vec x, t) = \dot{\vec b}(t)+\vec\omega(t)\times(\vec x-\vec b(t))</math> |
|||
Im Inertialsystem (blau in Abb 4), in dem der Bezugspunkt ruht und der Kreisel rotiert, werden die [[Euler-Winkel]] definiert, die die Orientierung der Hauptachsen des Kreisels im Raum angeben. Der zeitliche Verlauf der Winkel bestimmt die Bewegungsfunktion des Kreisels. Im raumfesten System können die Massenträgheitsmomente um nicht festgehaltene Achsen zeitlich variabel sein. |
|||
gegeben. Sie gibt zur Zeit ''t'' für ein Partikel am Ort <math>\vec x</math> die Geschwindigkeit <math>\vec v</math> an, die sich aus der Bewegung eines Bezugspunkts <math>\vec b(t)</math> und einer Drehung um ihn mit Winkelgeschwindigkeit <math>\vec\omega(t)</math> zusammen setzt. Das Rechenzeichen „ד bildet das [[Kreuzprodukt]]. In der Kreiseltheorie wird der Punkt <math>\vec b</math> festgehalten und in den Ursprung eines Koordinatensystems gelegt, sodass <math>\vec b\equiv\vec0</math> und die Geschwindigkeitsverteilung |
|||
Im mitrotierenden körperfesten Bezugssystem (rot) sind die Bewegungsgleichungen besonders leicht zu formulieren, weil dort die Trägheitsmomente zeitlich konstant sind. In den Bewegungsgleichungen müssen hier auftretende [[Trägheitskraft| Trägheitskräfte]] berücksichtigt werden. Diese sind die [[Euler-Kraft]] und die [[Fliehkraft]]. [[Corioliskraft| Corioliskräfte]] kommen hier nicht vor, weil beim Starrkörper eine Bewegung seiner Massenpunkte relativ zum Körper ausgeschlossen ist. |
|||
:<math>\vec v(\vec x, t) = \vec\omega(t)\times\vec x\,.</math> |
|||
In der Kreiseltheorie werden die Basisvektoren im raumfesten Bezugssystem mit den [[Eulersche Winkel#Geometrische Beschreibung|Euler’schen Winkeln]] in der Standard-x-Konvention (z, x', z") ausgedrückt, siehe Abb. 4. Der Winkel ''ψ'' ist der Präzessionswinkel, ''ϑ'' der Neigungswinkel und ''φ'' bestimmt die ''Eigendrehung'' des Kreisels. Bezeichnen die Einheitsvektoren ''ê''<sub>x,y,z</sub> die raumfeste [[Standardbasis]] (blau in Abb. 4) und ''ê''<sub>X,Y,Z</sub> = ''ê''<sub>1,2,3</sub> die mit dem Körper rotierende, bewegte Basis (rot in Abb. 4), dann lauten die mitbewegten Basiseinheitsvektoren bezüglich der raumfesten Basis: |
|||
gilt. Alle Partikel des Kreisels, die sich auf der Drehachse befinden (für die ist <math>\vec x\parallel\vec\omega</math>), ruhen solange sie das tun. Da die Drehachse nicht an die Partikel des Kreisels gebunden ist, kann sich die Drehachse relativ zum Kreisel bewegen, was eine wichtige Eigenschaft der Kreiselbewegung ist, die [[Präzession]] oder [[Nutation (Physik)| Nutation]] genannt wird, siehe oben. |
|||
:<math>\begin{align} |
|||
Speziell für die rotierenden Hauptachsen berechnen sich die Raten |
|||
\hat{e}_1=& \begin{pmatrix} |
|||
\cos(\psi)\cos(\varphi)-\sin(\psi)\cos(\vartheta)\sin(\varphi)\\ |
|||
\sin(\psi)\cos(\varphi)+\cos(\psi)\cos(\vartheta)\sin(\varphi)\\ |
|||
\sin(\vartheta)\sin(\varphi) |
|||
\end{pmatrix} |
|||
\\ |
|||
\hat{e}_2=& \begin{pmatrix} |
|||
-\cos(\psi)\sin(\varphi)-\sin(\psi)\cos(\vartheta)\cos(\varphi)\\ |
|||
-\sin(\psi)\sin(\varphi)+\cos(\psi)\cos(\vartheta)\cos(\varphi)\\ |
|||
\sin(\vartheta)\cos(\varphi) |
|||
\end{pmatrix} |
|||
\\ |
|||
\hat{e}_3=& \begin{pmatrix} |
|||
\sin(\psi)\sin(\vartheta)\\ |
|||
-\cos(\psi)\sin(\vartheta)\\ |
|||
\cos(\vartheta) |
|||
\end{pmatrix} |
|||
\end{align}</math> |
|||
Der Vektor |
|||
:<math>\dot{\hat e}_i: = \frac{\mathrm{d}}{\mathrm{d}t}{\hat e}_i = \vec v(\hat e_i, t) |
|||
= \vec\omega\times{\hat e}_i</math> |
|||
:<math>\hat e_N:=\frac{\hat e_z\times\hat e_3}{\sin(\vartheta)} |
|||
was analog auch für andere betraglich konstante körperfeste Vektoren gilt. |
|||
=\begin{pmatrix}\cos(\psi)\\ \sin(\psi)\\0\end{pmatrix}</math> |
|||
markiert die ''Knotenachse'' (gelbes ''N'' im Bild). Der Zusammenhang zwischen den Winkelgeschwindigkeiten und Vektoren ist |
|||
=== Bezugssysteme === |
|||
{{Hauptartikel| Bezugssystem}} |
|||
In der Kreiseltheorie werden vor allem drei Bezugssysteme verwendet: |
|||
Im Inertialsystem, in dem der Stützpunkt ruht und der Kreisel rotiert, werden die [[Euler-Winkel]] definiert, die die Position des Kreisels, also die Orientierung seiner Hauptachsen, im Raum angeben. Der zeitliche Verlauf der Winkel bestimmt dann die Bewegungsfunktion des Kreisels. In diesem System können die Massenträgheitsmomente um nicht festgehaltene Achsen zeitlich variabel sein. |
|||
Im mitrotierenden körperfesten Bezugssystem sind die Bewegungsgleichungen besonders leicht zu formulieren, denn nur dort sind die Trägheitsmomente zeitlich konstant. Die Bewegung wird hier durch zusätzlich wirkende [[Trägheitskraft|Trägheitskräfte]] beeinflusst. Diese sind die [[Euler-Kraft]] und die [[Fliehkraft]]. [[Corioliskraft|Corioliskräfte]] können nicht auftreten, weil beim Starrkörper eine Bewegung seiner Massenpunkte relativ zum Körper ausgeschlossen ist. |
|||
Gelegentlich wird bei symmetrischen Kreiseln noch ein anschauliches System verwendet, bei dem eine Achse mit der [[Figurenachse]] übereinstimmt, die anderen Achsen aber an der Rotation nicht teilnehmen. Hier wirken dann alle drei Formen der Trägheitskräfte: Euler-, Flieh- und Corioliskraft. |
|||
Die Bezugssysteme stellen sich mathematisch als [[Basisvektor]]en <math>\hat{g}_{1,2,3}</math> dar, mit denen vektorielle Größen ausgedrückt werden. Die Zeitableitung solcher vektorieller Größen, beispielsweise des Wegs <math>\vec r</math>, teilt sich im rotierenden Bezugssystem auf in einen Anteil, der auf die Relativbewegung im Bezugssystem zurückgeht, und einen zusätzlichen, der durch die Rotation des Bezugssystems beigetragen wird: |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\vec\omega=&\omega_1\hat e_1+\omega_2\hat e_2+\omega_3\hat e_3 |
|||
\dot{\vec r} |
|||
=\dot\psi\hat e_z+\dot\vartheta\hat e_N+\dot\varphi\hat e_3 |
|||
=& \frac{\mathrm{d}}{\mathrm{d}t}\sum_{i=1}^3r_i\hat{g}_i |
|||
\\ |
|||
= \sum_{i=1}^3\dot{r}_i\hat{g}_i+\sum_{i=1}^3r_i\dot{\hat{g}}_i |
|||
\omega_1=&\dot\psi\sin(\vartheta)\sin(\varphi)+\dot\vartheta\cos(\varphi) |
|||
= \frac{\mathrm{d}'}{\mathrm{d}t}\vec r+\vec\omega\times\vec r |
|||
\\ |
|||
\omega_2=&\dot\psi\sin(\vartheta)\cos(\varphi)-\dot\vartheta\sin(\varphi) |
|||
\\ |
|||
\omega_3=&\dot\psi\cos(\vartheta)+\dot\varphi |
|||
\\ |
|||
\dot{\psi}=&\frac{\omega_1\sin(\varphi)+\omega_2\cos(\varphi)}{\sin(\vartheta)} |
|||
\\ |
|||
\dot{\vartheta}=&\omega_1\cos(\varphi)-\omega_2\sin(\varphi) |
|||
\\ |
|||
\dot{\varphi}=&\omega_3-\dot{\psi}\cos(\vartheta) |
|||
\end{align}</math> |
\end{align}</math> |
||
Häufig werden die Komponenten ''ω''<sub>1,2,3</sub> im Hauptachsensystem auch mit ''p'', ''q'' und ''r'' bezeichnet und gelegentlich tauschen die Winkel ''ψ'' und ''φ'' die Bedeutung. |
|||
Darin ist <math>\tfrac{\mathrm{d}'}{\mathrm{d}t}</math> die „relative Zeitableitung“, die auch als <math>\tfrac{\mathrm{d}_r}{\mathrm{d}t}</math> notiert wird und bei der die Basisvektoren des Bezugssystems als konstant angenommen werden. Bei der Winkelgeschwindigkeit stimmen die Zeitableitung und die relative Zeitableitung im Hauptachsensystem überein: |
|||
Bei sin''ϑ'' = 0 tritt eine Singularität auf, weil dann, wegen cos''ϑ'' = ±1, die Winkel ''ψ'' und ''φ'' in den Basisvektoren nach den [[Formelsammlung Trigonometrie#Additionstheoreme| Additionstheoremen]] nur als Kombination ''ψ ± φ'' vorkommen und somit verschiedene Winkel zur selben Basis führen können. |
|||
:<math>\dot{\vec\omega} = \frac{\mathrm{d}'}{\mathrm{d}t}\vec\omega+\vec\omega\times\vec\omega |
|||
= \frac{\mathrm{d}'}{\mathrm{d}t}\vec\omega |
|||
= \sum_{i=1}^3\dot\omega_i\hat{e}_i |
|||
</math> |
|||
=== Euler’sche Geschwindigkeitsgleichung === |
|||
Darin stehen <math>\hat e_{1,2,3}</math> für das körperfeste, mitrotierende Hauptachsensystem. |
|||
Die Bewegungsfunktion starrer Körper ist durch die Euler’sche Geschwindigkeitsgleichung |
|||
:<math>\vec v(\vec x,t) |
|||
=== Freiheitsgrade des Kreisels === |
|||
=\dot{\vec b}(t)+\vec\omega(t)\times\big(\vec x-\vec b(t)\big)</math> |
|||
Der rotierende Kreisel besitzt fünf Freiheitsgrade: drei Winkel und die Position des Schwerpunkts relativ zum Stützpunkt, wobei der Abstand zwischen Schwer- und Stützpunkt konstant ist. Sind also fünf unabhängige Erhaltungsgrößen der Kreiselbewegung gefunden, dann ist die Bewegungsgleichung gelöst. Es genügen sogar nur vier, denn mit der Jacobi'schen Multiplikatoren Methode kann aus vier unabhängigen Integralen ein fünftes konstruiert werden.<ref group="L" name="kowalewskaja"/> |
|||
gegeben. Sie gibt zur Zeit ''t'' für ein Partikel am Ort <math>\vec x</math> die Geschwindigkeit <math>\vec v</math> an, die sich aus der Bewegung eines Bezugspunkts <math>\vec b(t)</math> und einer Drehung um ihn mit Winkelgeschwindigkeit <math>\vec\omega(t)</math> zusammen setzt. Das Rechenzeichen „ד bildet das [[Kreuzprodukt]] und der [[Punkt (Oberzeichen)#Als wissenschaftliches Symbol|Überpunkt]] bildet die [[Zeitableitung]]. Der Bezugspunkt <math>\vec b</math> kann in den Ursprung des Koordinatensystems gelegt werden und bei vernachlässigbarer Fortschreitbewegung <math>\dot{\vec b}</math> gilt die Geschwindigkeitsverteilung |
|||
== Kinetik von Kreiseln == |
|||
Die Kinetik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die von der Masse abhängen. |
|||
:<math>\vec v(\vec x, t)=\vec\omega(t)\times\vec x</math> |
|||
=== Trägheitstensor, Hauptträgheitsmomente und Hauptachsen === |
|||
{{Hauptartikel| Trägheitstensor}} |
|||
Der Trägheitstensor hat bei Drehbewegungen eine vergleichbare Rolle wie die Masse bei geradlinigen Bewegungen und ist deshalb eine zentrale Größe in der Kreiseltheorie. Bei einem aus einzelnen [[Massenpunkt]]en aufgebauten starren Körper berechnet sich der Trägheitstensor aus der Summe |
|||
Alle Partikel des Kreisels, die sich auf der Drehachse befinden (für die ist <math>\vec x\parallel\vec\omega</math>), ruhen solange sie das tun. Da die Drehachse nicht an die Partikel des Kreisels gebunden ist, kann sich die Drehachse relativ zum Kreisel bewegen, was eine wichtige Eigenschaft der Kreiselbewegung ist, die [[Präzession]] oder [[Nutation (Physik)| Nutation]] genannt wird. |
|||
:<math>\mathbf{\Theta} := \sum_i m_i[(\vec{r}_i\cdot\vec{r}_i)\mathbf{1}-\vec{r}_i\otimes\vec{r}_i] |
|||
= \sum_{i,j=1}^3\Theta_{ij}\hat g_i\otimes\hat g_j |
|||
= \sum_{i=1}^3\Theta_i\hat e_i\otimes\hat e_i |
|||
</math> |
|||
Speziell für betraglich konstante, körperfeste Vektoren verschwindet die [[Zeitableitung#Relative Zeitableitung|relative Zeitableitung]] und berechnen sich die Raten |
|||
Die Summe ist über alle Massenpunkte zu erstrecken, deren Position relativ zum Stützpunkt darin mit <math>\vec r_i</math> bezeichnet wird und ''m''<sub>i</sub> ist deren Masse. Diese Darstellung des Kreisels mittels ihn aufbauender Massenpunkte wird auch im Folgenden noch benutzt. |
|||
:<math>\dot{\vec r}:=\frac{\mathrm{d}}{\mathrm{d}t}\vec r |
|||
Die Vektoren <math>\hat g_{1,2,3}</math> sind eine beliebige Basis, das Rechenzeichen „·“ bildet das [[Skalarprodukt]], ⊗ das [[Dyadisches Produkt|dyadischen Produkt]]<ref group="F" name="dyade" /> von [[Vektor]]en und '''1''' ist der [[Einheitstensor]]. Die Komponenten Θ<sub>ij</sub> des Trägheitstensors sind in einem körperfesten System konstant, im Inertialsystem, in dem sich der Kreisel dreht, jedoch möglicherweise zeitabhängig. Die letzte Darstellung zeigt den Trägheitstensor in seiner Hauptachsendarstellung mit ''Hauptträgheitmomenten Θ''<sub>1,2,3</sub> und ''Hauptträgheitsachsen'' oder kurz Hauptachsen <math>\hat e_{1,2,3}</math>. Die Hauptachsen sind körperfest und drehen mit dem Kreisel mit. Der Trägheitstensor ist [[Symmetrische Matrix|symmetrisch]] und [[positiv definit]]. |
|||
=\vec v(\vec r, t)=\vec\omega\times\vec r</math> |
|||
== Kinetik von Kreiseln == |
|||
Alle [[Massenträgheitsmoment]]e, [[Drehimpuls]]e und [[Drehmoment]]e werden in der Kreiseltheorie immer bezüglich des Stützpunkts aufgestellt. |
|||
Die Theorie des Kreisels behandelt im Wesentlichen dessen [[Kinetik (Technische Mechanik)|Kinetik]]<ref name="grammel3"/>, die sich mit den von der Masse abhängenden Bewegungsgrößen und deren Beeinflussung durch Kräfte befasst. |
|||
=== Hauptträgheitsmomente, Hauptachsen und Trägheitstensor === |
|||
=== Drehimpuls von Kreiseln === |
|||
{{Hauptartikel| Trägheitstensor}} |
|||
Bei einem wie oben aus einzelnen Massenpunkten aufgebauten starren Körper kann mit obiger Geschwindigkeitsverteilung der Eigen­[[drehimpuls]] relativ zum Stützpunkt als Summe berechnet werden: |
|||
Jeder Starrkörper besitzt drei ausgezeichnete Achsen, die [[Hauptträgheitsachse|Hauptachsen]], die paarweise zueinander senkrecht sind oder orthogonalisierbar sind. Die Momente der [[Fliehkraft| Fliehkräfte]] gleichen sich bei der Drehung um die Hauptachsen genau aus, sodass sich der Kreisel gleichförmig um sie drehen kann. Eine von der Lage des [[Massenmittelpunkt]]s abhängige ''statische'' [[Unwucht]] mit entsprechenden ''Kraft''wirkungen in den Lagern ist dabei nicht ausgeschlossen. |
|||
Das Maß für den Widerstand des Kreisels gegen Rotationsänderungen sind seine [[Trägheitsmoment]]e, die bei den Hauptachsen [[Hauptträgheitsmoment]]e genannt und mit Θ<sub>1,2,3</sub> oder A, B und C bezeichnet werden. Die Hauptträgheitsmomente sind die [[Eigenwert]]e und die Hauptachsen ''ê''<sub>1,2,3</sub> die dazugehörigen [[Eigenvektor]]en des [[Trägheitstensor]]s, der in der Kreiseltheorie zumeist in der Hauptachsendarstellung mit [[Diagonalmatrix|Diagonalgestalt]] auftritt und beim rotierenden Kreisel eine vergleichbare Rolle übernimmt wie die Masse bei der Translation. Der Trägheitstensor bildet die Winkelgeschwindigkeit auf den Drehimpuls ab. Bei einem aus einzelnen [[Massenpunkt]]en aufgebauten starren Körper berechnet sich der Trägheitstensor aus der Summe |
|||
:<math> |
|||
\vec L |
|||
:= \sum_i\vec r_i\times\vec{p}_i |
|||
= \sum_i m_i\vec r_i\times(\vec\omega\times\vec{r}_i) |
|||
= \mathbf{\Theta}\cdot\vec\omega |
|||
</math> |
|||
Darin bezeichnet <math>\vec p_i = m_i\vec v_i = m_i\vec\omega\times\vec{r}_i</math> den aktuellen [[Impuls (Physik)|Impuls]] des ''i''-ten Massenpunkts. Ein Vergleich von <math>\vec p = m\vec v</math> mit <math>\vec L = \mathbf{\Theta}\cdot\vec\omega</math> zeigt, dass der Trägheitstensor für Drehungen eine vergleichbare Rolle wie die Masse für [[Translation (Physik)|Translationsbewegungen]] spielt. |
|||
=== Mechanische Energie von Kreiseln === |
|||
Die [[Rotationsenergie]] eines starren Körpers, der sich wie voraus gehend aus einzelnen Massenpunkten zusammen setzt, ergibt sich mit obiger Geschwindigkeitsverteilung zu |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\mathbf{\Theta} |
|||
E_\mathrm{rot} |
|||
:=&\sum_i m_i[(\vec r_i\cdot\vec r_i)\mathbf{1}-\vec r_i\otimes\vec r_i] |
|||
\\ |
|||
= \frac12\sum_i m_i(\vec\omega\times\vec{r}_i)^2 |
|||
=&\sum_{i,j=1}^3\Theta_{ij}\hat g_i\otimes\hat g_j |
|||
\\=& |
|||
=\sum_{i=1}^3\Theta_i\hat e_i\otimes\hat e_i |
|||
\frac12\vec\omega\cdot\mathbf{\Theta}\cdot\vec\omega |
|||
= \frac12\vec L\cdot\mathbf{\Theta}^{-1}\cdot\vec L |
|||
= \frac12\vec\omega\cdot\vec L |
|||
\end{align}</math> |
\end{align}</math> |
||
Die erste Summe ist über alle Massenpunkte zu erstrecken, wobei <math>\vec r_i</math> deren Position relativ zum Bezugspunkt ist und ''m''<sub>i</sub> deren Masse bedeutet. Die Vektoren ''ĝ''<sub>1,2,3</sub> sind eine beliebige Basis, das Rechenzeichen „·“ bildet das [[Skalarprodukt]], „⊗“ das [[Dyadisches Produkt|dyadische Produkt]] von [[Vektor]]en und '''1''' ist der [[Einheitstensor]]. Diese Darstellung des Kreisels mittels ihn aufbauender Massenpunkte wird auch im Folgenden noch benutzt. |
|||
Weil also bei einer Drehung das Skalarprodukt von Winkelgeschwindigkeit und Drehimpuls immer positiv ist, schließen sie immer einen spitzen Winkel ein. |
|||
Da die Positionen <math>\vec r_i</math> bei einer Rotation zeitabhängig sind, ist es der Trägheitstensor im Allgemeinen ebenfalls. Die Komponenten Θ<sub>''ij''</sub> sind konstant, wenn die Basisvektoren ''ĝ<sub>i</sub>'' körperfest sind, ansonsten zumeist zeitabhängig. Die letzte Darstellung zeigt den Trägheitstensor in seiner Hauptachsendarstellung mit Hauptträgheitsmomenten Θ<sub>''i''</sub> und Hauptachsen ''ê<sub>i</sub>''. Die Hauptachsen sind körperfest und drehen mit dem Kreisel mit. Der Trägheitstensor ist [[Symmetrische Matrix|symmetrisch]] und [[positiv definit]]. |
|||
In einem [[Schwerefeld]] mit konstanter Schwerebeschleunigung <math>\vec g</math> besitzt der Starrkörper die [[Lageenergie]] |
|||
Alle [[Massenträgheitsmoment]]e, [[Drehimpuls]]e und [[Drehmoment]]e werden in der Kreiseltheorie immer bezüglich des Stützpunkts oder des Massenmittelpunkts aufgestellt. |
|||
:<math> |
|||
E_\mathrm{pot} = -\sum_i m_i(\vec{r}_i\cdot\vec g) = -\vec g\cdot\sum_i m_i\vec{r}_i = -m\vec g\cdot\vec s |
|||
</math> |
|||
=== Drehimpuls und Rotationsenergie von Kreiseln === |
|||
Darin ist <math>\textstyle m := \sum_i m_i</math> die Masse und <math>\textstyle\vec s := \tfrac{1}{m}\sum_i m_i\vec{r}_i</math> der [[Massenmittelpunkt]] des Starrkörpers relativ zum Stützpunkt. Die Lageenergie nimmt also entgegen der Schwerebeschleunigung, im Schwerefeld der Erde also mit der Höhe, zu. Im körperfesten Hauptachsensystem haben die Schwerebeschleunigung und der Massenmittelpunkt die Koordinaten: |
|||
Bei einem wie oben aus einzelnen Massenpunkten aufgebauten starren Körper kann mit obiger Geschwindigkeitsverteilung und der [[Kreuzprodukt#Graßmann-Identität|BAC-CAB-Formel]] der Drehimpuls relativ zum Bezugspunkt als Summe berechnet werden:<ref name="dyade"/> |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\vec L=&\sum_i\vec r_i\times(m_i\vec\omega\times\vec r_i) |
|||
\vec g =& g(n_1{\hat e}_1+n_2{\hat e}_2+n_3{\hat e}_3),\quad g = |\vec g| |
|||
\\ |
\\ |
||
=&\sum_i m_i\big((\vec r_i\cdot\vec r_i)\vec\omega |
|||
\vec s =& s_1{\hat e}_1+s_2{\hat e}_2+s_3{\hat e}_3 |
|||
-(\vec r_i\cdot\vec\omega)\vec r_i\big) |
|||
=\mathbf{\Theta}\cdot\vec\omega |
|||
\end{align}</math> |
\end{align}</math> |
||
Darin ist <math>m_i\vec\omega\times\vec r_i=m_i\vec v_i=\vec p_i</math> der aktuelle [[Impuls (Physik)| Impuls]] des ''i''-ten Massenpunkts. Ein Vergleich von <math>\vec p=m\vec v</math> mit <math>\vec L=\mathbf{\Theta}\cdot\vec\omega</math> zeigt, dass der Trägheitstensor für Drehungen eine vergleichbare Rolle wie die Masse für [[Translation (Physik)| Translationsbewegungen]] spielt. Hier offenbart sich jedoch auch die Ursache dafür, dass die Kreiseltheorie sehr viel verwickelter ist als die Kinetik der Fortschreitbewegungen eines Starrkörpers, denn bei letzteren sind Impuls und Geschwindigkeit parallel, was bei Drehimpuls und Drehgeschwindigkeit im Allgemeinen nicht der Fall ist. Außerdem ist die Masse eine konstante Größe und der Trägheitstensor zumeist nicht, weshalb die Winkelgeschwindigkeit bei konstantem Drehimpuls zeitabhängig sein kann und umgekehrt. |
|||
mit Konstanten ''s''<sub>1,2,3</sub> im Hauptachsensystem. Damit lautet die Lageenergie |
|||
Die [[Rotationsenergie]] des Kreisels ergibt sich mit voraus gehender Zerlegung in einzelne Massenpunkte, der [[#Eulersche Geschwindigkeitsgleichung|Euler’schen Geschwindigkeitsgleichung]] und den Eigenschaften des [[Spatprodukt]]s zu |
|||
:<math>E_\mathrm{pot} = -m\vec g\cdot\vec s = -mg(s_1n_1+s_2n_2+s_3n_3)</math> |
|||
In der Literatur werden die Komponenten ''n''<sub>1,2,3</sub> der Schwerkraftrichtung auch mit <nowiki>γ, γ', γ''</nowiki> bezeichnet<ref group="L" name="kowalewskaja" />. |
|||
Wenn der Schwerpunkt der Stützpunkt ist (<math>\vec s = \vec0</math>), dann hat die Schwerebeschleunigung keinen Einfluss auf die Bewegung des Kreisels, was beim eulerschen Kreisel der Fall ist. Im Gegensatz dazu liegt beim ''schweren Kreisel'' der Schwerpunkt nicht im Stützpunkt und das Schwerefeld beeinflusst die Kreiselbewegung durch ein Moment |
|||
:<math> |
|||
\vec M = \vec s\times m\vec g |
|||
= mg\begin{pmatrix}s_2n_3-s_3n_2\\s_3n_1-s_1n_3\\s_1n_2-s_2n_1\end{pmatrix}_{\hat e_{1,2,3}} |
|||
</math> |
|||
Die letzte Darstellung als Spaltenvektor bezieht sich auf das Hauptachsensystem. |
|||
=== Schranken für Drehimpuls und Rotationsenergie === |
|||
Der Drehbewegung eines Kreisels kann jederzeit zum einen ein [[Drehimpuls]]­betrag <math>L := |\vec L|</math> und zum anderen eine [[Rotationsenergie]] <math>E_\mathrm{rot}</math> zugeordnet werden. Bei einem Kreisel liegen diese beiden Größen innerhalb der Schranken |
|||
:<math>2\Theta_1 E_\mathrm{rot}\le L^2\le 2\Theta_3 E_\mathrm{rot}</math> oder <math>\frac{L^2}{2\Theta_3}\le E_\mathrm{rot}\le\frac{L^2}{2\Theta_1}</math> |
|||
Darin wurde die übliche Anordnung Θ<sub>1</sub> < Θ<sub>2</sub> < Θ<sub>3</sub> der Hauptträgheitsmomente voraus gesetzt. |
|||
Denn im lokalen körperfesten Hauptachsensystem ausgedrückt gilt: |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
E_\mathrm{rot} |
|||
L^2 |
|||
:=&\frac12\sum_i m_i(\vec\omega\times\vec r_i)\cdot(\vec\omega\times\vec r_i) |
|||
&=& |
|||
=\frac12\vec\omega\cdot\sum_i m_i\vec r_i\times(\vec\omega\times\vec r_i) |
|||
\\=& |
|||
\ |
\frac12\vec\omega\cdot\mathbf{\Theta}\cdot\vec\omega |
||
=\frac12\vec L\cdot\mathbf{\Theta}^{-1}\cdot\vec L |
|||
\\ |
|||
=\frac12\vec\omega\cdot\vec L |
|||
2E_\mathrm{rot} |
|||
&=& |
|||
\vec\omega\cdot\mathbf{\Theta}\cdot\vec\omega |
|||
&=& |
|||
\Theta_1\omega^2_1+\Theta_2\omega^2_2+\Theta_3\omega^2_3 |
|||
\end{align}</math> |
\end{align}</math> |
||
Weil demnach das [[Skalarprodukt]] von Winkelgeschwindigkeit und Drehimpuls positiv ist, schließen sie einen spitzen Winkel ein. Die aktuelle Winkelgeschwindigkeit berührt überdies das zum Drehimpulsbetrag ''L'' gehörende [[Drallellipsoid]], sodass |
|||
Diese beiden Gleichungen stellen mathematisch [[Ellipsoid]]e dar, die erste das [[Trägheitsellipsoid#Drallellipsoid|Drallellipsoid]], die zweite das [[Energieellipsoid]], die im kräftefreien Fall – und nur dort – gleichbleibende Ausdehnung besitzen. Ein Punkt, der auf beiden Ellipsoiden liegt, muss die Bedingungen |
|||
:<math>(2E_\mathrm{rot}\Theta_1-L^2)\Theta_1\omega_1^2 |
|||
:<math>\begin{align} |
|||
1 |
|||
=& |
|||
\frac{1}{L^2}(\Theta_1^2\omega_1^2+\Theta_2^2\omega_2^2+\Theta_3^2\omega_3^2) |
|||
= |
|||
\frac{1}{2E_\mathrm{rot}}(\Theta_1\omega_1^2+\Theta_2\omega_2^2+\Theta_3\omega_3^2) |
|||
\\ |
|||
\rightarrow |
|||
0 |
|||
=& |
|||
(2E_\mathrm{rot}\Theta_1-L^2)\Theta_1\omega_1^2 |
|||
+(2E_\mathrm{rot}\Theta_2-L^2)\Theta_2\omega_2^2 |
+(2E_\mathrm{rot}\Theta_2-L^2)\Theta_2\omega_2^2 |
||
+(2E_\mathrm{rot}\Theta_3-L^2)\Theta_3\omega_3^2 |
+(2E_\mathrm{rot}\Theta_3-L^2)\Theta_3\omega_3^2 |
||
=0</math> |
|||
\\=& |
|||
2\left(E_\mathrm{rot}-\frac{L^2}{2\Theta_1}\right)\Theta_1^2\omega_1^2 |
|||
hält. Zum einen sind hieraus bei der Anordnung Θ<sub>1</sub> < Θ<sub>2</sub> < Θ<sub>3</sub> der Hauptträgheitsmomente die Schranken |
|||
+2\left(E_\mathrm{rot}-\frac{L^2}{2\Theta_2}\right)\Theta_2^2\omega_2^2 |
|||
+2\left(E_\mathrm{rot}-\frac{L^2}{2\Theta_3}\right)\Theta_3^2\omega_3^2 |
|||
:<math>2\Theta_1 E_\mathrm{rot}\le L^2\le 2\Theta_3 E_\mathrm{rot}</math> oder <math>\frac{L^2}{2\Theta_3}\le E_\mathrm{rot}\le\frac{L^2}{2\Theta_1}</math> |
|||
\end{align}</math> |
|||
ersichtlich, denn der kleinste Klammerausdruck kann nicht positiv und der größte nicht negativ sein. Zum anderen zeigt sich beim [[Euler-Kreisel]], dass der [[Spurkegel und Polkegel|Polkegel]], der aus den Punkten besteht, für die <math>X/\omega_1=Y/\omega_2=Z/\omega_3</math> ist, einen [[Schiefer Ellipsenkegel|Ellipsenkegel]] oder einen [[Kreiskegel]] darstellt<ref>Leimanis (1965), S. 11.</ref>, siehe [[#Bewegungen von Kreiseln mit Fixpunkt|Abb. 3]]. |
|||
erfüllen. In den letzten beiden Gleichungen sind alle Faktoren bis auf die Klammerausdrücke null oder positiv. Eine nicht-triviale Lösung existiert, wenn in den Gleichungen der kleinste Klammerausdruck nicht positiv und der größte nicht negativ ist. Mit den angenommenen Größenverhältnissen der Hauptträgheitsmomente stellen dies die obigen Schranken für das Drehimpulsbetragsquadrat und die Rotationsenergie sicher. Dann sind die Rotationsenergie und der Drehimpulsbetrag mit einer Drehbewegung des betrachteten Körpers verträglich. |
|||
=== Eulersche Kreiselgleichungen === |
=== Eulersche Kreiselgleichungen === |
||
{{Hauptartikel| Eulersche Gleichungen (Kreiseltheorie)}} |
{{Hauptartikel| Eulersche Gleichungen (Kreiseltheorie)}} |
||
Die Euler’schen Kreiselgleichungen ergeben sich aus dem [[Drallsatz]] <math>\vec M |
Die Euler’schen Kreiselgleichungen ergeben sich aus dem [[Drallsatz]] <math>\vec M=\dot{\vec L}=-\vec K</math>. Die [[#Kreiselwirkung]] auf der rechten Seite steht für Trägheitseffekte im [[Rotierendes Bezugssystem|rotierenden Bezugssystem]]:<ref name="talg">In der [[Formelsammlung Tensoralgebra#Kreuzprodukt eines Vektors mit einem Tensor|Tensoralgebra]] kann auf Klammerungen verzichtet werden:<br/> |
||
:<math>\vec\omega\times(\mathbf{\Theta}\cdot\vec\omega) |
|||
=(\vec\omega\times\mathbf{\Theta})\cdot\vec\omega |
|||
=\vec\omega\times\mathbf{\Theta}\cdot\vec\omega</math></ref> |
|||
:<math>\begin{align} |
:<math>\begin{align} |
||
\vec K |
\vec K=& \vec K_\text{Euler}+\vec K_\text{Zentrifugal} |
||
\\ |
\\ |
||
\vec K_\text{Euler} |
\vec K_\text{Euler}=& \sum_i\vec r_i\times[-m_i\dot{\vec\omega}\times\vec r_i] |
||
= |
=-\mathbf{\Theta}\cdot\dot{\vec\omega} |
||
= -\begin{pmatrix} |
|||
\Theta_1\dot{\omega}_1 \\ |
|||
\Theta_2\dot{\omega}_2 \\ |
|||
\Theta_3\dot{\omega}_3 |
|||
\end{pmatrix}_{\hat e_{1,2,3}} |
|||
\\ |
\\ |
||
\vec K_\text{Zentrifugal} |
\vec K_\text{Zentrifugal}=& |
||
\sum_i\vec r_i\times[-m_i\vec\omega\times(\vec\omega\times\vec r_i)] |
\sum_i\vec r_i\times[-m_i\vec\omega\times(\vec\omega\times\vec r_i)] |
||
= |
=-\vec\omega\times\mathbf{\Theta}\cdot\vec\omega |
||
= -\begin{pmatrix} |
|||
(\Theta_3-\Theta_2)\omega_2\omega_3\\ |
|||
(\Theta_1-\Theta_3)\omega_3\omega_1\\ |
|||
(\Theta_2-\Theta_1)\omega_1\omega_2 |
|||
\end{pmatrix}_{\hat e_{1,2,3}} |
|||
\end{align}</math> |
\end{align}</math> |
||
Die Vektoren in den eckigen Klammern stellen in der mittleren Gleichung die [[Euler-Kraft]] und unten die [[Zentrifugalkraft]] am Massenpunkt mit Masse ''m''<sub>i</sub> am Ort <math>\vec r_i</math> |
siehe [[Drallsatz#Drallsatz am Starren Körper|Drallsatz am starren Körper]]. Die Vektoren in den eckigen Klammern stellen in der mittleren Gleichung die [[Euler-Kraft]] und unten die [[Zentrifugalkraft]] am Massenpunkt mit Masse ''m''<sub>i</sub> am Ort <math>\vec r_i</math> dar. Würde der Kreisel mit konstant gehaltener Winkelgeschwindigkeit <math>\vec\omega</math> um die instantane Drehachse kreisen, dann würden die Zentrifugalkräfte ein resultierendes Moment haben, das gerade der obigen Summe entspricht. Da bei der wirklichen Bewegung die Drehachse jedoch ihre Lage beständig ändert, hat [[Louis Poinsot]] für diese Zentrifugalkräfte den Namen ''fiktive Zentrifugalkräfte'' vorgeschlagen.<ref name="edmw"/> |
||
In den Drallsatz eingesetzt |
In den Drallsatz eingesetzt entsteht mit den Kreiselwirkungen:<ref name="talg"/> |
||
:<math>\vec M |
:<math>\vec M=\dot{\vec L} |
||
= |
=\mathbf{\Theta}\cdot\dot{\vec\omega} |
||
+\vec\omega\times\underbrace{\mathbf{\Theta}\cdot\vec\omega}_{\vec L} |
|||
= |
=\frac{\mathrm{d}_r}{\mathrm{d}t}\vec L |
||
+\underbrace{\vec L\cdot\mathbf{\Theta}^{-1}}_{\vec\omega}\times\vec L |
|||
</math> |
</math> |
||
Darin bildet <math>\tfrac{\mathrm{d}_r}{\mathrm{d}t}</math> die [[Zeitableitung#Relative Zeitableitung| relative Zeitableitung]] im körperfesten Hauptachsensystem. Die Komponenten dieser Vektorgleichung sind im Hauptartikel nachzuschlagen. |
|||
oder im körperfesten Hauptachsensystem ausgeschrieben: |
|||
=== Integrale der Bewegung === |
|||
:<math>\begin{align} |
|||
In der Kreiseltheorie werden bei der Rotation eines Kreisels unveränderliche [[physikalische Größe]]n ''Integrale'', manchmal auch ''erste Integrale'' genannt, {{enS|first integrals}}<ref name="richter2525"/>. Diese sind von hervorragender Bedeutung, weil sie die Lösung der Kreiselgleichungen ermöglichen oder zumindest, wie das [[Spielkreisel#Jelletts Integral|Jellett-Integral beim Spielkreisel]], die Bewegungen klassifizieren. |
|||
M_1 =& \Theta_1\dot{\omega}_1+(\Theta_3-\Theta_2)\omega_2\omega_3 |
|||
= \dot L_1+\left(\frac{1}{\Theta_2}-\frac{1}{\Theta_3}\right)L_2L_3 |
|||
\\ |
|||
M_2 =& \Theta_2\dot{\omega}_2+(\Theta_1-\Theta_3)\omega_3\omega_1 |
|||
= \dot L_2+\left(\frac{1}{\Theta_3}-\frac{1}{\Theta_1}\right)L_3L_1 |
|||
\\ |
|||
M_3 =& \Theta_3\dot{\omega}_3+(\Theta_2-\Theta_1)\omega_1\omega_2 |
|||
= \dot L_3+\left(\frac{1}{\Theta_1}-\frac{1}{\Theta_2}\right)L_1L_2 |
|||
\end{align}</math> |
|||
Beim [[Euler-Kreisel]] ist <math>\vec M=\dot{\vec L}=\vec0</math> und somit der Drehimpuls konstant. Der Drehimpuls, seine raumfesten Komponenten und sein Betrag sind bei dem Kreisel Integrale. Wenn das [[Schwerefeld]] [[Konservative Kraft|konservativ]] ist, so wie das der Erde, befolgt die Kreiselbewegung den [[Energieerhaltungssatz]], weshalb die [[Gesamtenergie]] dann ein Integral ist. Beim [[Schwerer Kreisel|schweren Kreisel]] hat das Moment der lotrechten Schwerkraft keine Komponente in [[Lotrichtung]] und somit ist der Drehimpuls in dieser Richtung ein Integral. Jedoch besitzen die Integrale, wie beispielsweise die [[Kowalewskaja-Kreisel#Integrale der Bewegung|Kowalewskaja-Konstante]], nicht immer eine anschauliche Bedeutung. |
|||
Darin sind jeweils für k=1,2,3 |
|||
:''M''<sub>k</sub> die von außen angreifenden Drehmomente, |
|||
:Θ<sub>k</sub> die Hauptträgheitsmomente, |
|||
:''L''<sub>k</sub> := Θ<sub>k</sub>''ω''<sub>k</sub> die Drehimpulse, |
|||
:''ω''<sub>k</sub> die [[Winkelgeschwindigkeit]]en und |
|||
: <math>\dot\omega_{k}</math> die [[Winkelbeschleunigung]]en |
|||
im Hauptachsensystem. |
|||
=== Lagrange- und Hamiltonfunktion des Kreisels === |
=== Lagrange- und Hamiltonfunktion des Kreisels === |
||
| Zeile 360: | Zeile 304: | ||
:<math>\mathcal{L} |
:<math>\mathcal{L} |
||
= |
=E_\mathrm{rot}-E_\mathrm{pot} |
||
= |
=\frac{L_1^2}{2\Theta_1}+\frac{L_2^2}{2\Theta_2}+\frac{L_3^2}{2\Theta_3} |
||
-mg(s_1n_1+s_2n_2+s_3n_3) |
|||
</math> |
</math> |
||
Darin sind jeweils für k=1,2,3 |
|||
:Θ<sub>k</sub> die Hauptträgheitsmomente, |
|||
:''L''<sub>k</sub> die Drehimpulse, |
|||
:''n''<sub>k</sub> die [[Richtungskosinus]] des [[lotrecht]] nach ''oben'' weisenden Einheitsvektors und |
|||
:''s''<sub>k</sub> die Koordinaten des Massenmittelpunkts |
|||
im Hauptachsensystem. |
|||
Die Lagrange-Funktion kann mit den [[Euler-Winkel]]n ausgedrückt werden, deren zeitlicher Verlauf dann aus den Lagrangegleichungen resultieren. |
Die Lagrange-Funktion kann mit den [[Euler-Winkel]]n ausgedrückt werden, deren zeitlicher Verlauf dann aus den Lagrangegleichungen resultieren. |
||
| Zeile 368: | Zeile 320: | ||
Die Hamiltonfunktion ''H'' des Kreisels ist die Summe aus Rotationsenergie und der potentiellen Energie: |
Die Hamiltonfunktion ''H'' des Kreisels ist die Summe aus Rotationsenergie und der potentiellen Energie: |
||
:<math>H=E_\mathrm{rot}+E_\mathrm{pot} |
|||
:<math> |
|||
=\frac{L_1^2}{2\Theta_1}+\frac{L_2^2}{2\Theta_2}+\frac{L_3^2}{2\Theta_3} |
|||
H |
|||
+mg(s_1n_1+s_2n_2+s_3n_3) |
|||
= E_\mathrm{rot}+E_\mathrm{pot} |
|||
= \frac{L_1^2}{2\Theta_1}+\frac{L_2^2}{2\Theta_2}+\frac{L_3^2}{2\Theta_3}-mg(s_1n_1+s_2n_2+s_3n_3) |
|||
</math> |
</math> |
||
Die Euler-Poisson |
Die [[Euler-Poisson-Gleichungen]] können mit ihr und der [[Poisson-Klammer]] {} ausgedrückt werden: |
||
:<math>\dot{L}_i=\{L_i, H\},\quad \dot{n}_i=\{n_i, H\} |
|||
:<math> |
|||
</math> für ''i'' = 1, 2, 3 |
|||
\dot{L}_i = \{L_i, H\},\quad \dot{n}_i = \{n_i, H\}\quad\text{für}\; i = 1,2,3 |
|||
</math> |
|||
Diese Bewegungsgleichungen lassen sich auch in der Vektorform<ref |
Diese Bewegungsgleichungen lassen sich auch in der Vektorform<ref name="Frechet"/> |
||
:<math>\begin{align} |
:<math>\begin{align} |
||
\dot M |
\dot M=& M\times\frac{\partial H}{\partial M}+\gamma\times\frac{\partial H}{\partial\gamma} |
||
\\ |
\\ |
||
\dot\gamma |
\dot\gamma=& \gamma\times\frac{\partial H}{\partial M} |
||
\end{align}</math> |
\end{align}</math> |
||
| Zeile 392: | Zeile 342: | ||
:<math> |
:<math> |
||
\{L_i, L_j\} |
\{L_i, L_j\}=-\varepsilon_{ijk} L_k,\quad\{L_i, n_j\}=-\varepsilon_{ijk} n_k, |
||
\quad\{n_i, n_j\} |
\quad\{n_i, n_j\}=0 |
||
</math> |
</math> |
||
Darin ist ε<sub>ijk</sub> das [[Levi-Civita-Symbol]]. Es gibt zwei Casimir Funktionen F<sub>1</sub> |
Darin ist ''ε''<sub>ijk</sub> das [[Levi-Civita-Symbol]]. Es gibt zwei Casimir Funktionen F<sub>1</sub> = M · γ und F<sub>2</sub> = γ², die bezüglich der Poisson-Klammer mit jeder Funktion von M und γ kommutieren und die auch gleichzeitig Integrale der Hamiltonfunktion sind.<ref>Borisov und Mamaev (2001), S. 254.</ref> |
||
== Lösungen der Kreiselgleichungen == |
|||
Für die technische Anwendung gibt es bedeutsame Spezialfälle, bei denen sich die Kreiselgleichungen soweit vereinfachen, dass sie [[integrabel]] sind. In diesen Fällen weisen die [[Trajektorie (Physik)| Trajektorien]] des Kreisels einen periodischen Verlauf auf, können die verschiedenen Bewegungsmodi klassifiziert und die Zeitfunktionen der Variablen sowie ihre geometrische Bedeutung angegeben werden. Insbesondere beim Kowalewskaja-Kreisel und im Goryachew-Chaplygin Fall sind die analytischen Lösungen so kompliziert, dass die Herausarbeitung der vorgenannten typischen Eigenschaften der Bewegung äußerst aufwändig ist. Hier helfen topologische Analyse ([[Bifurkationsdiagramm]]), [[Stabilitätstheorie| Stabilitätsanalyse]], [[Phasenraum]]-Diagramme und [[Computeranimation]]en dabei, Einblicke in die Vorgänge im Kreisel zu erhalten und deren typischen Eigenschaften heraus zu arbeiten. Die so erzielten Ergebnisse können praktische Anwendungen motivieren<ref group="L" name="borisov" />. |
|||
Die folgende Tabelle gibt eine Übersicht über die Fälle, in denen bisher exakte Lösungen der Bewegungsgleichungen gelungen sind<ref group="F">Magnus (1971), S. 108.</ref>. |
|||
{| class="wikitable" |
|||
|- |
|||
! Entdecker !! Hauptträgheits-<br/>momente !! Lage des<br/>Schwerpunkts !! Anfangs­be­din­gung­en (''t'' = 0) |
|||
|- |
|||
| [[Leonhard Euler| Euler]]<br/>siehe [[Euler-Kreisel]] || beliebig |
|||
| ''s''<sub>1</sub>=''s''<sub>2</sub>=''s''<sub>3</sub>=0 || beliebig |
|||
|- |
|||
| [[Joseph-Louis Lagrange| Lagrange]]<br/>siehe [[Lagrange-Kreisel]] |
|||
| A=B || ''s''<sub>1</sub>=''s''<sub>2</sub>=0, ''s''<sub>3</sub>≠0 || beliebig |
|||
|- |
|||
| [[Sofia Kowalewskaja| Kowalewskaja]]<br/>siehe [[Kowalewskaja-Kreisel]]|| A=B=2C |
|||
| <math>s_1^2+s_2^2\ne0,\,s_3=0</math> || beliebig |
|||
|- |
|||
| [[Wilhelm Hess (Mathematiker)|Wilhelm Hess]]<br/>siehe [[Hesssches Pendel]] || beliebig |
|||
| <math>\frac{s_1}{s_3}=\sqrt{\frac{C(A-B)}{A(B-C)}}</math><br/>''s''<sub>2</sub>=0 |
|||
| <math>\vec L\cdot\vec s=0</math> |
|||
|- |
|||
| [[Dmitri Nikanorowitsch Gorjatschew|Gorjatschew]] und [[Sergei Alexejewitsch Tschaplygin|Chaplygin]]<br/> |
|||
siehe [[Gorjatschew-Tschaplygin-Kreisel]] |
|||
| A=B=4C || <math>s_1^2+s_2^2\ne0,\,s_3=0</math> || ''L''<sub>z</sub>=0 |
|||
|- |
|||
| [[Nikolai Iwanowitsch Merzalow|Merzalow]] || A=B=4C || <math>s_1^2+s_2^2\ne0,\,s_3=0</math> |
|||
| ''ω''<sub>3</sub> = 0 |
|||
|- |
|||
| Bobylev und [[Wladimir Andrejewitsch Steklow|Steklow]]<br/>siehe [[Bobylew-Steklow-Lösung]] |
|||
| 2A=C || ''s''<sub>1</sub>=''s''<sub>2</sub>=0, ''s''<sub>3</sub>≠0 || <math>\dot\omega_2=\omega_2=0</math> |
|||
|- |
|||
| [[Otto Staude| Staude]]<br/>siehe [[Staude-Drehung]] || beliebig || beliebig |
|||
| <math>\vec\omega\times\hat e_z=0</math><br/><math>(\vec\omega\times\vec L)\cdot\vec s=0</math> |
|||
|- |
|||
| [[Giuseppe Grioli| Grioli]]<br/>siehe [[Griolische Präzession]] |
|||
| beliebig |
|||
| <math>\frac{s_1}{s_3}=\sqrt{\frac{A-B}{B-C}}</math><br/>''s''<sub>2</sub>=0 |
|||
| Bis auf einen Freiheitsgrad eindeutig festgelegt |
|||
|} |
|||
== Fußnoten == |
== Fußnoten == |
||
<references responsive |
<references responsive> |
||
<ref name=" |
<ref name="Darmstaedter">{{Literatur |
||
| Hrsg=[[Ludwig Darmstaedter]] |
|||
Das dyadische Produkt ist mit drei beliebigen Vektoren <math>\vec a,\vec b,\vec c</math> definiert durch <math>(\vec a\otimes\vec b)\cdot\vec c := (\vec b\cdot\vec c)\vec a</math></ref> |
|||
| Titel=Handbuch zur Geschichte der Naturwissenschaften und Technik |
|||
<ref name="Frechet"> |
|||
| Verlag=Springer-Verlag |
|||
Die [[Fréchet-Ableitung]] einer skalaren Funktion <math> f(\vec v) </math> nach einem Vektor <math>\vec v</math> |
|||
| Ort=Berlin, Heidelberg |
|||
ist der Vektor <math>\vec A</math> für den - sofern er existiert - gilt: |
|||
| Jahr=1908 |
|||
| Online=https://commons.wikimedia.org/wiki/File%3AHandbuch_zur_Geschichte_der_Naturwissenschaften_und_der_Technik.pdf |
|||
:<math>\vec A\cdot\vec h |
|||
| Seiten=209 |
|||
=\left.\frac{\mathrm{d}}{\mathrm{d}s}f(\vec v+s\vec h)\right|_{s=0} |
|||
| Zugriff=2020-01-19}} |
|||
=\lim_{s\rightarrow0} |
|||
\frac{f(\vec v+s\vec h)-f(\vec v)}{s} |
|||
\quad\forall\; |
|||
\vec h</math> |
|||
Darin ist <math>s\in\mathbb{R}</math> und „·“ das [[Frobenius-Skalarprodukt]]. Dann wird auch |
|||
:<math>\frac{\partial f}{\partial\vec v}=\vec A</math> |
|||
geschrieben. |
|||
</ref> |
</ref> |
||
</references> |
|||
= |
<ref name="Truesdell">{{Literatur |
||
| Autor=[[Clifford Truesdell]] |
|||
<references group="L"> |
|||
| Titel=Die Entwicklung des Drallsatzes |
|||
<ref name="magnus1971"> |
|||
| Herausgeber=[[Gesellschaft für Angewandte Mathematik und Mechanik]] |
|||
{{Literatur |
|||
| Sammelwerk=[[Zeitschrift für Angewandte Mathematik und Mechanik]] |
|||
| Autor=[[Kurt Magnus (Ingenieur)| K. Magnus]] |
|||
| Band=44 |
|||
| Titel=Kreisel: Theorie und Anwendungen |
|||
| Jahr=1964 |
|||
| Verlag=Springer |
|||
| Monat=4 |
|||
| Datum=1971 |
|||
| Reihe=Heft 4/5 |
|||
| Seiten=v |
|||
| Seiten=154 |
|||
| ISBN=978-3-642-52163-8 |
|||
| Online=http://onlinelibrary.wiley.com/doi/10.1002/zamm.19640440402/abstract |
|||
| Online={{Google Buch| BuchID=tATNBgAAQBAJ| Seite=v}} |
|||
| DOI=10.1002/zamm.19640440402}}</ref> |
|||
| Zugriff=2018-02-20 |
|||
}} |
|||
</ref> |
|||
<ref name=" |
<ref name="euler">{{Literatur |
||
| Autor=[[Leonhard Euler]] |
|||
{{Literatur |
|||
| Herausgeber=[[Königlich Preußische Akademie der Wissenschaften zu Berlin]] |
|||
| Autor=[[Felix Klein| F. Klein]], [[Arnold Sommerfeld| A. Sommerfeld]] |
|||
| Titel=Über die Bewegung der Rotation von starren Körpern um eine variable Achse |
|||
| Titel=The Theory of the Top |
|||
| Sammelwerk=Mémoires de l’Académie des Sciences de Berlin |
|||
| TitelErg=Development of the Theory in the Case of the Heavy Symmetric Top |
|||
| Ort=Petersburg |
|||
| Sprache=en |
|||
| Jahr=1758 |
|||
| Übersetzer=R. J. Nagem, G. Sandri |
|||
| Band=14 |
|||
| Seiten=173 und 190. |
|||
| Verlag=Birkhäuser |
|||
| Sprache=fr |
|||
| Ort=Boston |
|||
| Originaltitel=Du mouvement de rotation des corps solides autour d'un axe variable |
|||
| Datum=2010 |
|||
| Online=https://archive.org/details/euler-e292 |
|||
| Seiten=291 |
|||
| Zugriff=2020-01-11}} |
|||
| ISBN=978-0-8176-4824-4 |
|||
| DOI=10.1007/978-0-8176-4827-5 |
|||
}} |
|||
</ref> |
</ref> |
||
<ref name=" |
<ref name="lagrange"> |
||
{{Literatur |
{{Literatur |
||
| Autor=[[ |
| Autor=[[Joseph-Louis Lagrange]] |
||
| Titel= |
| Titel=Mécanique Analytique |
||
| Band=Tome Second |
|||
| TitelErg=Seine Theorie und seine Anwendungen |
|||
| Verlag= |
| Verlag=Corucier |
||
| Ort= |
| Ort=Paris |
||
| Datum= |
| Datum=1815 |
||
| Seiten= |
| Seiten=265f |
||
| Sprache=fr |
|||
| Online=https://archive.org/details/derkreiselseine00gramgoog |
|||
| Online=https://archive.org/details/mcaniqueanalyti05lagrgoog |
|||
| Kommentar=„Schwung“ bedeutet Drehimpuls, „Drehstoß“ Drehmoment und „Drehwucht“ Rotationsenergie |
|||
| Abruf=2017-08-20}} oder {{Literatur |
|||
| DNB=451641280}} |
|||
| Autor=Joseph-Louis Lagrange |
|||
oder |
|||
| Titel=Analytische Mechanik |
|||
{{Literatur |
|||
| Verlag=Vandenhoeck und Ruprecht |
|||
| Autor=[[Richard Grammel| R. Grammel]] |
|||
| Ort=Göttingen |
|||
| Titel=Der Kreisel |
|||
| Datum=1797 |
|||
| TitelErg=Seine Theorie und seine Anwendungen |
|||
| Kommentar=Deutsche Übersetzung von Friedrich Murhard |
|||
| Band=Band 2. |
|||
| Online=https://archive.org/details/analytischemech00murhgoog |
|||
| Auflage=2. überarb. Aufl. |
|||
| Abruf=2017-08-20}} |
|||
| Verlag=Springer |
|||
| Ort=Berlin, Göttingen, Heidelberg |
|||
| Datum=1950 |
|||
}} |
|||
</ref> |
</ref> |
||
<ref name=" |
<ref name="husson"> |
||
{{Literatur |
{{Literatur |
||
| Autor=Édouard Husson |
|||
| Titel=Forschung nach algebraischen Integralen in der Bewegung eines schweren Körpers um einen festen Punkt |
|||
| Titel=Euler-Poisson Equations and Integrable Cases |
|||
| Originaltitel=Recherche des intégrales algébriques dans le mouvement d’un solide pesant autour d’un point fixe |
|||
| Datum=2001 |
|||
| Sammelwerk=Annales de la faculté des sciences de Toulouse 2<sup>e</sup> série |
|||
| Sprache=en |
|||
| DOI=10.5802/afst.232 |
|||
| Kommentar=Enthält Lösungen der Kreiselgleichungen, deren ausführliche Beschreibung und weiter führende Literaturangaben. |
|||
| Datum=1906 |
|||
| arxiv=nlin/0502030 |
|||
| Seiten=73–152 |
|||
| DOI=10.1070/RD2001v006n03ABEH000176}} |
|||
| Online=http://archive.numdam.org/article/AFST_1906_2_8__73_0.pdf |
|||
| Zugriff=2018-03-07 |
|||
| Sprache=fr |
|||
| Kommentar=Auf Seite 74 wird ein erster Beweisversuch von [[Roger Liouville]] 1897 als fehlerhaft aufgedeckt |
|||
}}, siehe auch Audin (2008), S. 106. |
|||
</ref> |
</ref> |
||
<ref name=" |
<ref name="magnus1963">{{Literatur |
||
| Autor=[[Kurt Magnus (Ingenieur)| K. Magnus]] |
|||
{{Literatur |
|||
| Titel=Kreiselprobleme/ Gyrodynamics |
|||
| Autor=Wilderich Tuschmann, Peter Hawig |
|||
| TitelErg=Symposion Celerina, 20. Bis 23. August 1962 / Symposion Celerina, August 20–23, 1962 |
|||
| Titel=[[Sofia Kowalewskaja]] |
|||
| Verlag=Springer Verlag |
|||
| TitelErg=Ein Leben für Mathematik und Emanzipation |
|||
| Hrsg=Hans Ziegler |
|||
| Verlag=Birkhäuser Verlag |
|||
| Ort=Berlin u. a. |
|||
| Datum=1963 |
|||
| Seiten=7 |
|||
| ISBN=978-3-0348-5721-5 |
|||
| ISBN=978-3-662-12200-6 |
|||
| Online={{Google Buch|BuchID=G62bBgAAQBAJ| Seite=119}} |
|||
| DOI=10.1007/978-3-662-12200-6 |
|||
| Online={{Google Buch| BuchID=iJ-FBwAAQBAJ| Seite=4}} |
|||
| Abruf=2017-05-25}} |
|||
</ref> |
}}</ref> |
||
<ref name="magnus1962"> |
|||
{{Literatur |
|||
| Autor=[[Kurt Magnus (Ingenieur)| K. Magnus]] |
|||
| Titel=Kreiselprobleme / Gyrodynamics |
|||
| TitelErg=Symposion Celerina, 20. Bis 23. August 1962 / Symposion Celerina, August 20–23, 1962 |
|||
| Verlag=Springer Verlag |
|||
| Hrsg=Hans Ziegler |
|||
| Ort=Berlin u. a. |
|||
| ISBN=978-3-662-12200-6 |
|||
| DOI=10.1007/978-3-662-12200-6 |
|||
| Datum=1963 |
|||
| Seiten=7 |
|||
| Online={{Google Buch| BuchID=iJ-FBwAAQBAJ| Seite=4}} |
|||
}} |
|||
</ref> |
|||
<ref name="heiberg"> |
|||
{{Literatur |
|||
| Autor=[[Johan Ludvig Heiberg (Philologe)|J. L. Heiberg]] |
|||
| Hrsg=[[Hans-Joachim Gehrke]], [[Bernhard Zimmermann]] |
|||
| Titel=Geschichte der Mathematik und Naturwissenschaften im Altertum |
|||
| Sammelwerk=[[Handbuch der Altertumswissenschaft]] |
|||
| Band=5. Band, erste Abteilung zweite Hälfte |
|||
| Verlag=[[Verlag C.H.Beck]] |
|||
| Ort=München |
|||
| Datum=1925}} |
|||
</ref> |
|||
<ref name="lagrange"> |
|||
{{Literatur |
|||
| Autor=[[Joseph-Louis Lagrange]] |
|||
| Titel=Mécanique Analytique |
|||
| Band=Tome Second |
|||
| Verlag=Corucier |
|||
| Ort=Paris |
|||
| Datum=1815 |
|||
| Seiten=265f |
|||
| Sprache=fr |
|||
| Online=https://archive.org/details/mcaniqueanalyti05lagrgoog |
|||
| Abruf=2017-08-20}} oder {{Literatur |
|||
| Autor=Joseph-Louis Lagrange |
|||
| Titel=Analytische Mechanik |
|||
| Verlag=Vandenhoeck und Ruprecht |
|||
| Ort=Göttingen |
|||
| Datum=1797 |
|||
| Kommentar=Deutsche Übersetzung von Friedrich Murhard |
|||
| Online=https://archive.org/details/analytischemech00murhgoog |
|||
| Abruf=2017-08-20}} |
|||
</ref> |
|||
<ref name="präzession"> |
<ref name="präzession"> |
||
{{Internetquelle |
{{Internetquelle |
||
| url=http://www.duden.de/rechtschreibung/Praezession |
|||
| titel=Duden│Präzession |
|||
| hrsg=Duden online |
|||
| zugriff=2017-11-05}} |
|||
sowie |
sowie |
||
{{Internetquelle |
{{Internetquelle |
||
| url=http://www.duden.de/rechtschreibung/Nutation |
|||
| titel=Duden│Nutation |
|||
| hrsg=Duden online |
|||
| zugriff=2018-03-08}} |
|||
</ref> |
|||
<ref name="autenrieth"> |
|||
{{Literatur |
|||
| Autor=[[Edmund Friedrich Autenrieth| E. F. Autenrieth]], Max Ensslin |
|||
| Titel=Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure |
|||
| Verlag=Springer-Verlag |
|||
| Ort=Berlin |
|||
| Jahr=1922 |
|||
| ISBN=978-3-642-98876-9 |
|||
| Online={{Google Buch| BuchID=OTeuBgAAQBAJ| Seite=423}} |
|||
| Zugriff=2017-11-05 |
|||
}}</ref> |
|||
<ref group="L" name="sommer" > |
|||
{{Literatur |
|||
| Autor=[[Felix Klein| F. Klein]], [[Arnold Sommerfeld| A. Sommerfeld]] |
|||
| Titel=Theorie des Kreisels |
|||
| TitelErg=Die technischen Anwendungen der Kreiseltheorie |
|||
| Band=Heft IV. |
|||
| Verlag=Teubner |
|||
| Ort=Leipzig |
|||
| Datum=1910 |
|||
| Seiten=762 |
|||
| Online=https://archive.org/details/fkleinundasommer019696mbp |
|||
| Abruf=2017-10-21 |
|||
}}</ref> |
|||
<ref group="L" name="kuypers"> |
|||
{{Literatur |
|||
| Autor=Friedhelm Kuypers |
|||
| Titel=Klassische Mechanik |
|||
| Verlag=Wiley-VCH |
|||
| Ort=Weinheim |
|||
| Datum=2016 |
|||
| ISBN=978-3-527-33960-0 |
|||
| Online={{Google Buch| BuchID=haHcCwAAQBAJ| Seite=215}} |
|||
| Abruf=2017-11-07 |
|||
}}</ref> |
|||
<ref group="L" name="truesdell"> |
|||
{{Literatur |
|||
| Autor=[[Clifford Truesdell]] |
|||
| Titel=Die Entwicklung des Drallsatzes |
|||
| Herausgeber=[[Gesellschaft für Angewandte Mathematik und Mechanik]] |
|||
| Sammelwerk=[[Zeitschrift für Angewandte Mathematik und Mechanik]] |
|||
| Band=44 |
|||
| Jahr=1964 |
|||
| Monat=4 |
|||
| Reihe=Heft 4/5 |
|||
| Seiten=149 – 158 |
|||
| Online=http://onlinelibrary.wiley.com/doi/10.1002/zamm.19640440402/abstract |
|||
| DOI=10.1002/zamm.19640440402 |
|||
}}</ref> |
|||
<ref group="L" name="staeckel"> |
|||
{{Literatur |
|||
| Autor=[[Felix Klein]], Conr. Müller |
|||
| Titel=Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen |
|||
| TitelErg=Mechanik |
|||
| Herausgeber=Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien |
|||
| Band=Vierter Band |
|||
| Verlag=Springer Verlag |
|||
| Jahr=2013 |
|||
| ISBN=978-3-663-16021-2 |
|||
| DOI=10.1007/978-3-663-16021-2 |
|||
| Seiten=581ff |
|||
| Online={{Google Buch| BuchID=j1aVBwAAQBAJ| Seite=581}} |
|||
| Zugriff=2018-01-12 |
|||
}}</ref> |
|||
<ref name="husson"> |
|||
{{Literatur |
|||
| Autor=Édouard Husson |
|||
| Titel=Recherche des intégrales algébriques dans le mouvement d’un solide pesant autour d’un point fixe |
|||
| Sammelwerk=Annales de la faculté des sciences de Toulouse 2<sup>e</sup> série |
|||
| DOI=10.5802/afst.232 |
|||
| Datum=1906 |
|||
| Seiten=73–152 |
|||
| Online=http://archive.numdam.org/article/AFST_1906_2_8__73_0.pdf |
|||
| Zugriff=2018-03-07 |
|||
| Sprache=fr |
|||
| Kommentar=Auf Seite 74 wird ein erster Beweisversuch von [[Roger Liouville]] 1897 als fehlerhaft aufgedeckt. |
|||
}}<br/> |
|||
siehe auch<br/> |
|||
{{Literatur |
|||
| Autor=Michèle Audin |
|||
| Titel=Remembering Sofya Kovalevskaya |
|||
| Verlag=Springer Verlag |
|||
| Ort= London u. a. |
|||
| ISBN=978-0-85729-928-4 |
|||
| DOI=10.1007/978-0-85729-929-1 |
|||
| Datum=2008 |
|||
| Seiten=106 |
|||
| Online={{Google Buch| BuchID=sfqMyhrVuu8C| Seite=106}} |
|||
| Sprache=en |
|||
}} |
|||
</ref> |
|||
<ref name="interessen"> |
|||
{{Internetquelle |
|||
| autor=A. Beuthner, P. H. Richter |
|||
| hrsg=Universität Bremen |
|||
| url=http://www-nonlinear.physik.uni-bremen.de/forschung.html |
|||
| titel=Institut für Theoretische Physik |
|||
| zugriff=2018-03-07 |
|||
| archiv-url=https://web.archive.org/web/20171026041912/http://www-nonlinear.physik.uni-bremen.de/forschung.html |
|||
| archiv-datum=2017-10-26 |
|||
| offline=ja |
|||
| archiv-bot=2019-04-24 01:29:24 InternetArchiveBot |
|||
}} |
|||
</ref> |
|||
<ref name="richter2006"> |
|||
{{Internetquelle |
|||
| autor=P. H. Richter |
|||
| hrsg=Institut für theoretische Physik, Universität Bremen |
|||
| url=http://www-nonlinear.physik.uni-bremen.de/download/RigidBodyDynamics.pdf |
|||
| format=pdf |
|||
| sprache=en |
|||
| titel=Regular and Chaotic Rigid Body Dynamics |
|||
| zugriff=2018-03-08 |
|||
| archiv-url=https://web.archive.org/web/20170808060406/http://www-nonlinear.physik.uni-bremen.de/download/RigidBodyDynamics.pdf |
|||
| archiv-datum=2017-08-08 |
|||
| offline=ja |
|||
| archiv-bot=2019-04-24 01:29:24 InternetArchiveBot |
|||
}} |
|||
</ref> |
</ref> |
||
| Zeile 745: | Zeile 465: | ||
| ISBN=978-3-0348-6670-5 |
| ISBN=978-3-0348-6670-5 |
||
| DOI=10.1007/978-3-0348-6669-9 |
| DOI=10.1007/978-3-0348-6669-9 |
||
| Online={{Google Buch| BuchID=pkqgBgAAQBAJ| Seite= |
| Online={{Google Buch| BuchID=pkqgBgAAQBAJ| Seite=159}} |
||
| Zugriff=2018-02-14 |
| Zugriff=2018-02-14 |
||
| Originaltitel=Математическе методы классическоя механики |
| Originaltitel=Математическе методы классическоя механики |
||
| Zeile 751: | Zeile 471: | ||
| Originaljahr=1979 |
| Originaljahr=1979 |
||
| Originalort=Moskau |
| Originalort=Moskau |
||
| Übersetzer=Prof. Dr. Peter Möbius, TU Dresden |
| Übersetzer=Prof. Dr. Peter Möbius, TU Dresden}} |
||
}} |
|||
</ref> |
</ref> |
||
<ref name="edmw"> |
|||
{{Literatur |
|||
| Autor=[[Felix Klein]], Conr. Müller |
|||
| Titel=Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen |
|||
| TitelErg=Mechanik |
|||
| Herausgeber=[[Akademie der Wissenschaften zu Göttingen|Akademien der Wissenschaften zu Göttingen]], Leipzig, München und Wien |
|||
| Band=Vierter Band |
|||
| Nummer=1. Teilband |
|||
| Verlag=Springer Verlag |
|||
| Jahr=2013 |
|||
| ISBN=978-3-663-16021-2 |
|||
| DOI=10.1007/978-3-663-16021-2 |
|||
| Seiten=586 |
|||
| Online={{Google Buch| BuchID=j1aVBwAAQBAJ| Seite=586}} |
|||
| Zugriff=2020-01-24 |
|||
| Kommentar=siehe auch [https://de.wikisource.org/wiki/Encyklop%C3%A4die_der_mathematischen_Wissenschaften wikisource]}} |
|||
</ref> |
|||
<ref name="magnus109">Magnus (1971), S. 109.</ref> |
|||
<ref name="dyade"> |
|||
Das dyadische Produkt ist mit drei beliebigen Vektoren <math>\vec a,\vec b,\vec c</math> definiert durch <math>(\vec a\otimes\vec b)\cdot\vec c:=(\vec b\cdot\vec c)\vec a</math></ref> |
|||
<ref name="Frechet"> |
|||
Die [[Fréchet-Ableitung]] einer skalaren Funktion <math> f(\vec v) </math> nach einem Vektor <math>\vec v</math> |
|||
ist der Vektor <math>\vec A</math> für den - sofern er existiert - gilt: |
|||
:<math>\vec A\cdot\vec h |
|||
=\left.\frac{\mathrm{d}}{\mathrm{d}s}f(\vec v+s\vec h)\right|_{s=0} |
|||
=\lim_{s\rightarrow0} |
|||
\frac{f(\vec v+s\vec h)-f(\vec v)}{s} |
|||
\quad\forall\; |
|||
\vec h</math> |
|||
Darin ist <math>s\in\mathbb R</math> und „·“ das [[Frobenius-Skalarprodukt]]. Dann wird auch |
|||
:<math>\frac{\partial f}{\partial\vec v}=\vec A</math> |
|||
geschrieben. |
|||
</ref> |
|||
</references> |
</references> |
||
== Literatur == |
|||
* {{Literatur |
|||
| Autor=[[Richard Grammel| R. Grammel]] |
|||
| Titel=Der Kreisel |
|||
| TitelErg=Seine Theorie und seine Anwendungen |
|||
| Verlag=Vieweg Verlag |
|||
| Ort=Braunschweig |
|||
| Datum=1920 |
|||
| Online=https://archive.org/details/derkreiselseine00gramgoog |
|||
| Kommentar="Schwung" bedeutet Drehimpuls, "[[Drehstoß]]" etwa Drehmoment und "Drehwucht" Rotationsenergie, siehe S. VII |
|||
| DNB=573533210}}<br/>oder<br/>{{Literatur |
|||
| Autor=[[Richard Grammel|R. Grammel]] |
|||
| Titel=Der Kreisel |
|||
| TitelErg=Seine Theorie und seine Anwendungen |
|||
| Band=Erster Band: Die Theorie des Kreisels |
|||
| Verlag=Springer Verlag |
|||
| Ort=Berlin u. a. |
|||
| Datum=1950 |
|||
| Online={{Google Buch|BuchID=SmvOBgAAQBAJ|Seite=3}} |
|||
| Zugriff=2020-01-19 |
|||
| ISBN=978-3-662-24311-4 |
|||
| DOI=10.1007/978-3-662-26425-6}} |
|||
* {{Literatur |
|||
| Autor=[[Kurt Magnus (Ingenieur)| K. Magnus]] |
|||
| Titel=Kreisel: Theorie und Anwendungen |
|||
| Verlag=Springer |
|||
| Datum=1971 |
|||
| Seiten=v |
|||
| ISBN=978-3-642-52163-8 |
|||
| Online={{Google Buch| BuchID=tATNBgAAQBAJ| Seite=1}} |
|||
| Zugriff=2020-01-19}} |
|||
* {{Literatur |
|||
| Autor=Wilderich Tuschmann, Peter Hawig |
|||
| Titel=[[Sofia Kowalewskaja]] |
|||
| TitelErg=Ein Leben für Mathematik und Emanzipation |
|||
| Verlag=Birkhäuser Verlag |
|||
| Ort=Basel |
|||
| Datum=1993 |
|||
| ISBN=978-3-0348-5721-5 |
|||
| Online={{Google Buch| BuchID=G62bBgAAQBAJ| Seite=119}} |
|||
| DOI=10.1007/978-3-0348-5720-8 |
|||
| Abruf=2017-05-25}} |
|||
* {{Literatur |
|||
| Autor=[[Felix Klein| F. Klein]], [[Arnold Sommerfeld| A. Sommerfeld]] |
|||
| Titel=Über die Theorie des Kreisels |
|||
| Band=Heft I-III |
|||
| Verlag=Teubner |
|||
| Ort=Leipzig |
|||
| Datum=1897 |
|||
| Online=https://archive.org/details/abv7354.0001.001.umich.edu/ |
|||
| Abruf=2020-01-17}}<br/>Sowie</br>{{Literatur |
|||
| Autor=[[Felix Klein| F. Klein]], [[Arnold Sommerfeld| A. Sommerfeld]] |
|||
| Titel=Über die Theorie des Kreisels |
|||
| Band=Heft IV |
|||
| Verlag=Teubner |
|||
| Ort=Leipzig |
|||
| Datum=1910 |
|||
| Online=https://archive.org/details/fkleinundasommer019696mbp |
|||
| Abruf=2020-01-17}} |
|||
* {{Literatur |
|||
| Autor=Friedhelm Kuypers |
|||
| Titel=Klassische Mechanik |
|||
| Verlag=Wiley-VCH |
|||
| Ort=Weinheim |
|||
| Datum=2016 |
|||
| ISBN=978-3-527-33960-0 |
|||
| Online={{Google Buch| BuchID=haHcCwAAQBAJ| Seite=215}} |
|||
| Abruf=2017-11-07}} |
|||
* {{Literatur |
|||
| Autor=Eugene Leimanis |
|||
| Titel=The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point |
|||
| Verlag=Springer Verlag |
|||
| Ort=Berlin, Heidelberg |
|||
| Jahr=1965 |
|||
| ISBN=978-3-642-88414-6 |
|||
| Seiten=10 f. |
|||
| DOI=10.1007/978-3-642-88412-2 |
|||
| Sprache=en |
|||
| Online={{Google Buch| BuchID=s8rsCAAAQBAJ| Seite=53}} |
|||
| Zugriff=2018-03-21}} |
|||
* {{Literatur |
|||
| Autor=I. G. Gashenenko, [[Peter Richter (Physiker)| P. H. Richter]] |
|||
| Titel=Enveloping Surfaces And Admissible Velocities Of Heavy Rigid Bodies |
|||
| Herausgeber=World Scientific Publishing Company |
|||
| Sammelwerk=International Journal of Bifurcation and Chaos |
|||
| Band=14 |
|||
| Nummer=8 |
|||
| Jahr=2004 |
|||
| ISSN=0218-1274 |
|||
| Seiten=2525–2553 |
|||
| Kommentar=siehe S. 2537 |
|||
| DOI=10.1142/S021812740401103X |
|||
| Online=http://iamm.su/upload/iblock/fb1/gas_rich.pdf |
|||
| Zugriff=2019-06-02}} |
|||
* {{Literatur |
|||
| Autor=A. V. Borisov, I. S. Mamaev |
|||
| Titel=Euler-Poisson Equations and Integrable Cases |
|||
| Datum=2001 |
|||
| Sprache=en |
|||
| Kommentar=Enthält Lösungen der Kreiselgleichungen, deren ausführliche Beschreibung und weiter führende Literaturangaben. |
|||
| arxiv=nlin/0502030 |
|||
| DOI=10.1070/RD2001v006n03ABEH000176}} |
|||
* {{Literatur |
|||
| Autor=[[Edmund Friedrich Autenrieth| E. F. Autenrieth]], Max Ensslin |
|||
| Titel=Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure |
|||
| Verlag=Springer-Verlag |
|||
| Ort=Berlin |
|||
| Jahr=1922 |
|||
| ISBN=978-3-642-98876-9 |
|||
| Online={{Google Buch| BuchID=OTeuBgAAQBAJ| Seite=423}} |
|||
| Zugriff=2017-11-05}} |
|||
* {{Literatur |
|||
| Autor=Michèle Audin |
|||
| Titel=Erinnerungen an Sofja Kowalewskaja |
|||
| Originaltitel=Remembering Sofya Kovalevskaya |
|||
| Verlag=Springer Verlag |
|||
| Ort=London u. a. |
|||
| ISBN=978-0-85729-928-4 |
|||
| DOI=10.1007/978-0-85729-929-1 |
|||
| Datum=2008 |
|||
| Seiten=106 |
|||
| Online={{Google Buch| BuchID=sfqMyhrVuu8C| Seite=106}} |
|||
| Sprache=en}} |
|||
== Weblinks == |
== Weblinks == |
||
| Zeile 761: | Zeile 644: | ||
[[Kategorie:Kreiseltheorie| ]] |
[[Kategorie:Kreiseltheorie| ]] |
||
[[Kategorie:Klassische Mechanik]] |
|||
Version vom 28. Januar 2020, 20:29 Uhr
Die Kreiseltheorie beschäftigt sich mit rotierenden Körpern, bei denen translatorische Bewegungen und Verformungen von untergeordneter Bedeutung sind.[1]
Körper, auf die diese Beschreibung zutrifft, werden in der Theorie zusammenfassend als Kreisel bezeichnet und beinhalten so verschiedene Objekte wie Spielkreisel, Langgeschosse oder die Erde. Die Kreiselbewegungen sind für Mathematik, Physik und Ingenieurwesen – somit für Theorie und Praxis – gleichermaßen attraktiv. Ziel der Theorie ist es, Anwendungen auf eine sichere Grundlage zu stellen[2].
Leonhard Euler begründete 1750 die (analytische) Kreiseltheorie mit den nach ihm benannten Kreiselgleichungen, die im körperfesten Bezugssystem die Winkelbeschleunigungen mit den angreifenden Drehmomenten verbinden. Darauf aufbauend definiert die Kreiseltheorie Eigenschaften von Kreiseln (Massenmittelpunkt, Hauptachsen, …), deren Kinematik (Euler-Winkel, Winkelgeschwindigkeit, …) und Kinetik (Trägheitsellipsoid, Euler-Poisson-Gleichungen, …), leitet, auch mit dem Lagrange-Formalismus, Bewegungsfunktionen der Kreisel ab und gibt Methoden (Poinsotsche Konstruktion, Phasenraumportraits, …), diese anschaulich darzustellen.
Anwendungen findet die Kreiseltheorie in der Eisenbahntechnik (Sinuslauf), der Drallstabilisierung von Schiffen (Schiffskreisel), Raumflugkörpern und Trägheitsnavigationssystemen sowie in der Astronomie und Ballistik.
Geschichte
Leonhard Euler entwickelte 1736 eine Theorie der Präzession[3] und 1750 die Kreiselgleichungen[4], die er 1758 für den kräftefreien Euler-Kreisel lösen oder zumindest auf elliptische Integrale zurückführen konnte[5]. Joseph-Louis Lagrange leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den schweren symmetrischen Kreisel mit Fixpunkt[6]. Carl Gustav Jacob Jacobi veröffentlichte 1829 die Theorie der elliptischen-Funktionen und der Theta-Funktionen, mit denen sich die Kreiselgleichungen lösen lassen. Das hat Jacobi am Euler-Kreisel demonstriert und er empfahl 1849 mehrfach, das Problem mit diesen Funktionen anzugehen[7]. Zwischenzeitlich veröffentlichte Siméon Denis Poisson 1838 seine kinematischen Gleichungen[8], die die Kreiselgleichungen zu den Euler-Poisson-Gleichungen vervollständigen.
Trotz des vielversprechenden Ansatzes mit Theta-Funktionen und Preisausschreiben der preußischen und russischen Akademie der Wissenschaften in den 1850er Jahren erwies sich die „mathematische Nixe“, wie das „Kreiselproblem“ in Deutschland mittlerweile aufgrund seiner Attraktivität und Unnahbarkeit tituliert wurde, als äußerst unzugänglich[9]. Sofia Kowalewskaja entdeckte 1888 den letzten durch Theta-Funktionen lösbaren Fall, den schweren, symmetrischen, inhomogenen Kowalewskaja-Kreisel, womit die analytische Kreiseltheorie zu einem gewissen Abschluss kam[10]. So sind die Standardwerke von Klein und Sommerfeld (entstanden 1896-1910), Richard Grammel (1920, 1950) oder Kurt Magnus (1971) noch zu Beginn des 21. Jahrhunderts benutzbar. Ein Beleg dafür ist, dass ersteres Werk noch 100 Jahre nach seinem Erscheinen ins englische übersetzt wurde.[11]
A. M. Ljapunow bewies 1894, dass die drei Fälle von Euler, Lagrange und Kowalewskaja die einzigen sind, in denen die Lösung der Euler-Poisson-Gleichungen bei beliebigen Anfangsbedingungen eine eindeutige Funktion der Zeit ist, und É. Husson zeigte 1905[12], dass diese Kreisel auch die einzigen mit algebraischen Integralen lösbaren Fälle sind. Somit gelingt die Lösung mittels algebraischer Integrale nur in den Fällen, wo die Bewegung eine eindeutige Funktion der Zeit ist[13]. Darüber hinaus können nur spezielle Bewegungen integrabel sein. Um 1900 haben Mathematiker viele neue integrierbare Spezialfälle gefunden[14], aber die Frage nach der Lösbarkeit der großen Mehrheit der Kreiselbewegungen bleibt bis ins 21. Jahrhundert hinein offen.[15]
Wenngleich sich die klassische Kreiseltheorie überwiegend mit dem starren Körper mit Fixpunkt befasste, so wurden doch auch kreiselähnliche Erscheinungen an rotierenden Ketten, verformbaren Körpern – insbesondere der Erde – oder Flüssigkeiten untersucht. Durch die Raumfahrt kamen neue Problemstellungen hinzu[16], wie beispielsweise
- die Selbsterregung (im körperfesten System aufgebrachte Momente) zwecks Stabilisierung und Lageregelung, siehe Stabilisierung (Raumfahrt),
- die Bewegungen von Körpern mit veränderlichen Massen,
- die Bewegungen starrer Körper mit Flüssigkeitsfüllung,
- die Drehbewegungen in einem zentralen Schwerefeld oder
- die Beeinflussung von Translations- und Rotationsbewegungen.
Ab Mitte des 20. Jahrhunderts entwickelten sich die Computerhard- und -software und mit ihnen die numerische Simulation soweit, dass mit ihrer Hilfe die Bewegungsgleichungen bei beliebigen Anfangsbedingungen und jeder gewünschten Genauigkeit berechnet werden können[17]. Die analytischen Lösungen verloren nun die früher berechtigte, zentrale Bedeutung und die nicht integrablen Fälle rückten in den Fokus. Analytische und geometrische Methoden zu ihrer Untersuchung entstanden, die auch immer wieder durch den Kowalewskaja-Kreisel motiviert waren, der die Wissenschaft das gesamte 20. Jahrhundert hindurch beschäftigte. Die Untersuchungsmethoden der integrablen Fälle wurden zu Beginn des 21. Jahrhunderts auf die nicht integrablen dynamischen Systeme übertragen.[18]
Eigenschaften der Kreisel und ihrer Bewegungen
Die Kreiseltheorie versteht unter einem Kreisel einen beliebig gestalteten starren Körper, der Drehbewegungen ausführt. Dieses idealisierende Modell für wirkliche Kreisel ermöglicht deren Verhalten mit einfacheren mathematischen Hilfsmitteln zu erfassen[19]. Die klassische Kreiseltheorie konzentrierte sich auf den schweren Kreisel, der in einem Inertialsystem in einem seiner Punkte derart festgehalten wird, dass er sich um diesen Punkt noch irgendwie drehen kann[20]. Diese Forderung stellt nur eine kleine Einschränkung dar, denn jede Starrkörperbewegung lässt sich in Rotation und Translation zerlegen, und sofern letztere (näherungsweise) gleichförmig ist, spielt sie für die Kreiselbewegung keine Rolle. Durch die Fixierung in einem Punkt verringert sich die Anzahl der Freiheitsgrade des Starrkörpers von sechs auf drei.
Die Geschwindigkeit der Drehbewegung ist in der Kreiseltheorie unwesentlich. Der relativ langsam umlaufende „Erdkreisel“ unterliegt den Kreiselgesetzen genauso wie ein mit 60.000 U/min rotierender technischer Kreisel, allerdings vereinfachen sich die Gestzmäßigkeiten bei diesen sogenannten schnellen Kreiseln außerordentlich[21]. Die Trägheitseigenschaften von Kreiseln lassen sich anschaulich durch Ellipsoide darstellen:
- am Trägheitsellipsoid können die Trägheitsmomente abgelesen werden,
- das Massenellipsoid hat dieselben Trägheitseigenschaften wie der betrachtete Körper,
- das Energieellipsoid besteht aus allen Drehgeschwindigkeiten und
- das MacCullagh-Ellipsoid aus allen Drehimpulsen, die zur selben Rotationsenergie führen.
Die Ellipsoide rotieren mit dem Kreisel mit und die Lage der Halbachsen sowie ihre relativen Längen sind wichtige, den Kreisel charakterisierende physikalische Größen. Denn eine Koordinate des Massenmittelpunkts kann dazu verwendet werden, die Längen im Modell zu skalieren, und ein Hauptträgheitsmoment, um die Zeit oder Energie zu skalieren[22]. Zwei Kreisel mit zueinander ähnlichen Ellipsoiden und vergleichbarer Lage des Massenmittelpunkts bewegen sich daher ähnlich. Das motiviert die vielen Begriffe zur Beschreibung der Massenverteilung von Kreiseln, wie symmetrischer und unsymmetrischer Kreisel, die noch prolat oder oblat bzw. lang-, mittel- oder kurzachsig sein können.
Drehgeschwindigkeit und Drehimpuls
Die Winkelgeschwindigkeit lässt sich kompakt als Vektor ausdrücken: Seine Richtung definiert die Drehachse und sein Betrag die Drehgeschwindigkeit um diese Achse. Gleiches gilt für den Drehimpuls, der ein Maß für den Schwung des Kreisels ist und der ebenfalls Richtung und Betrag besitzt.
Die Dynamik des Kreisels lässt sich mit dem Drehimpuls ähnlich der Dynamik des Massenpunkts formulieren:[23]
- Der kräftefreie Kreisel bewegt sich so, dass sein Drehimpuls nach Betrag und Richtung konstant bleibt (so wie sich ein kräftefreier Massenpunkt gleichförmig bewegt).
- Unter dem Einfluss von Drehmomenten bewegt sich der Kreisel derart, dass die Änderungsgeschwindigkeit des Drehimpulsvektors nach Richtung und Betrag gleich dem angreifenden Moment ist (so wie die Beschleunigung des Massenpunkts in Richtung einer angreifenden Kraft erfolgt).
Die Analogien zwischen Rotation und Translationsbewegung hören jedoch dort auf, wo die typischen Kreiselbewegungen beginnen. Denn während Impuls und Geschwindigkeit bei der Translation immer parallel und proportional zueinander sind, trifft das auf Drehimpuls und Drehgeschwindigkeit in den kreiseltheoretisch interessanten Fällen nicht zu. Wird ein anfangs ruhender Kreisel durch einen Drehstoß um eine Achse in Drehung versetzt, muss er anschließend keineswegs um diese Achse kreisen[24]. Bei konstantem Drehimpuls muss die Winkelgeschwindigkeit mitnichten konstant sein und umgekehrt, was der Dschanibekow-Effekt eindrücklich untermauert, siehe auch #Drehimpuls und Rotationsenergie von Kreiseln.
Drallsatz

Das in der Kreiseltheorie wichtigste physikalische Gesetz ist der Drallsatz, der sich beim Kreisel als Regel vom gleichsinnigen Parallelismus[25] ausdrückt, siehe Abb. 1.: Greift am Kreisel ein Drehmoment M an, dann versucht der Kreisel seine Drehbewegung, ausgedrückt durch den Drehimpuls L, dem Drehsinn des Moments gleichsinnig parallel auszurichten, was im Bild blau angedeutet ist. Aus diesem Grundsatz leiten sich viele Eigenschaften der Kreiselbewegungen ab. Wirkt auf den Kreisel beispielsweise eine Kraft, dann ist das von ihr ausgeübte Drehmoment senkrecht zu ihr und somit weicht ein rotierender Kreisel einer Kraft immer senkrecht zu ihrer Wirkungslinie aus. Das gilt jedoch nur für den Drehimpuls und nicht notwendigerweise auch für die Drehachse oder eine Symmetrieachse des Kreisels.
Der Drallsatz besagt, dass um den Drehimpuls eines Kreisels zu verändern, ein Drehmoment angreifen muss. Ohne solche Momente bleibt der Drehimpuls in Betrag und Richtung erhalten. Aus dem Drallsatz leiten sich auch die Euler’schen Kreiselgleichungen ab, mit denen die rechnerische Behandlung der Kreiselbewegungen erfolgt. Der Drehimpuls und die Drehachse sind nur in Spezialfällen parallel. Im Allgemeinen gilt:
- Bei konstantem Drehimpuls ändert sich bei freier Bewegung fortlaufend die Drehachse und der Kreisel taumelt oder „eiert“.
- Wird die Drehachse festgehalten, dann ändert sich fortlaufend der Drehimpuls, wofür die Halterungen der Drehachse die dazu notwendigen Momente einbringen und die Kreiselwirkungen abtragen müssen.
Kreiselwirkung
Das auffälligste Merkmal von Kreiseln ist die des gyroskopischen Effekts oder der Kreiselwirkung, die sich als verblüffende Kraftäußerung bemerkbar macht, wenn man versucht, die Drehachse eines Kreisels in eine neue Lage zu bringen. Die Kreiselwirkung äußert sich dabei als Widerstand, der über das beim ruhenden Körper bekannte Maß weit hinausgehen kann[26].
Die Kreiselwirkung versucht nach der Regel des gleichsinnigen Parallelismus die Achse der Eigendrehung in Richtung und Orientierung mit der Achse der erzwungenen Drehung zur Deckung zu bringen[27]. Die Kreiselwirkung ist eine d’Alembertsche Trägheitskraft und als solche ein einem angreifenden Moment entgegengesetzt gleichgroßes Moment: Moment und Kreiselwirkung befinden sich im dynamischen Gleichgewicht.
Die Kreiselwirkung ist gleich der Summe der im Körper durch die Euler- und Zentrifugalkräfte ausgeübten Momente, siehe #Euler’sche Kreiselgleichungen. In den Richtungen senkrecht zum angreifenden Moment neutralisieren sich die Kreiselwirkungen der Euler- und Zentrifugalkräfte und befinden sich dort untereinander im dynamischen Gleichgewicht. Die Euler-Kräfte sind Ausdruck von Winkelbeschleunigungen, die dort von den Zentrifugalkräften im Kreisel hervorgerufen werden. Umgekehrt führen die Winkelbeschleunigungen zur Änderung der Drehachse und Drehgeschwindigkeit, was die Zentrifugalkräfte beeinflusst. Auswirkung dieses dynamischen Wechselspiels ist besagtes Taumeln und „Eiern“ des kräftefreien Kreisels. Die Kreiselwirkungen werden bei Kurvenkreiseln, Kollermühlen und der Drallstabilisierung technisch ausgenutzt.
Drallstabilisierung

Eine der technisch wertvollsten Eigenschaften von Kreiseln ist die Möglichkeit, mit ihnen Körper in ihrer räumlichen Ausrichtung zu stabilisieren. Dies wird, wie schon eingangs erwähnt, bei Schiffen, Raumflugkörpern und Geschossen ausgenutzt.
Um die Drallstabilisierung zu erläutern, wird die Bewegung des Schwungrads in Abb. 2 betrachtet, wobei die Figurenachse (anfänglich in y-Richtung) frei ist, so dass sie ihre Richtung beliebig ändern kann. Auf dieses ansonsten kräftefreie Schwungrad wirke eine kurze Zeit in z-Richtung ein konstantes Moment Mz, das das Schwungrad in Drehung um z versetzt. Diese Drehung macht sich am ruhenden und rotierenden Schwungrad jedoch unterschiedlich bemerkbar:
- Ruht das Schwungrad, dann beginnt es durch das Moment um z zu rotieren. Nachdem das Moment aufgehört hat zu wirken, verharrt das Schwungrad in der Drehung um z, es gibt keine Kreiselwirkung und der Drehwinkel ψ der Figurenachse um z nimmt monoton zu und ist unbeschränkt. Die Winkelgeschwindigkeit und der Drehimpuls haben nur eine Komponente und die weist in z-Richtung. Der Neigungswinkel ϑ zwischen Figurenachse und Momentenachse z bleibt unverändert.
- Rotiert das Schwungrad anfänglich hinreichend schnell um die Figurenachse, dann zeigt sich ein anderes Bild. Zwar führt das Moment auch hier zu einer linearen Zunahme des Drehimpulses in z-Richtung, aber weil sich diese Komponente zum anfänglichen (als viel größer angenommenen) Drehimpuls in y-Richtung vektoriell addiert, der Drehimpuls also weiter vor allem in y-Richtung orientiert ist, und Drehimpuls und Winkelgeschwindigkeit einen spitzen Winkel einschließen (siehe #Drall und Rotationsenergie von Kreiseln), dreht das Schwungrad weiter vor allem um die y-Achse. Dadurch bleibt der Drehwinkel ψ der Figurenachse um z beschränkt. Nach der Regel vom gleichsinnigen Parallelismus versucht der Kreisel seine Drehung dem angreifenden Moment anzugleichen, wodurch der Winkel ϑ abnimmt.
Ursache für den geringen Einfluss des Moments auf die Drehung des rotierenden Schwungrads um z sind Trägheitskräfte, die Kreiselwirkungen aufbauen. Wird die Drehachse durch Lager irgendwie gehalten, neutralisieren sie diese Kreiselwirkungen und können die Trägheitskräfte nicht ihr Potenzial entfalten. Drallstabilisierung tritt nur bei Kreiseln auf, die ihre volle Bewegungsfreiheit in drei Drehfreiheitsgraden besitzen[28]. Aber selbst dann gelingt eine Drallstabilisierung nicht immer, wie William Thomson, 1. Baron Kelvin und Peter Guthrie Tait zeigen konnten.[29]
Bewegungen von Kreiseln mit Fixpunkt

Betrachtet werden freie Bewegungen, bei denen die Drehachse ihre Richtung ändern kann.
Die Bewegungen des kräftefreien Kreisels werden in der Kreiseltheorie Nutation genannt und die fremderregten Präzession[30][31]. Allerdings sind diese Bezeichnungen nicht einheitlich. Arnold[32] beispielsweise nennt die periodische Änderung der Neigung der Figurenachse gegenüber der Lotlinie beim Lagrange-Kreisel Nutation und die azimutale Drehung Präzession.
Die Drehachse eines Kreisels ist nicht körperfest, sie kann sich also relativ zum Kreisel bewegen und überstreicht dabei den körperfesten Gangpolkegel oder kurz Polkegel. Gleichzeitig bewegt sich die Drehachse auch im Raum und erzeugt dadurch eine Fläche, den Rastpol- oder Spurkegel. Die Leitkurve der Kegel ist der Endpunkt des Winkelgeschwindigkeitsvektors, der teils chaotisch schwankt, nur selten einen Zustand zweimal einnimmt und beliebig geformte Spurkegel und Polkegel erzeugt. Beim Kreisel mit Fixpunkt befinden sich die Spitzen der Kegel in diesem Punkt und der Polkegel rollt schlupflos auf dem Spurkegel ab[33]. Beim symmetrischen Euler-Kreisel sind die Kegel Kreiskegel und die Bewegung besonders anschaulich, siehe Bild.
Der kräftefreie Kreisel befolgt mangels äußerer Einwirkungen den Energieerhaltungssatz. Solche Erhaltungsgrößen sind in der Kreiseltheorie von großem Interesse und werden #Integrale der Bewegung genannt. Dem Spielkreisel nahe verwandt ist der Lagrange-Kreisel, an dem paradoxe Kreiselerscheinungen auffallen:
- die Präzession mit horizontaler Figurenachse und
- das Auffrichten des Kreisels entgegen der Schwerkraft.
Beim Kowalewskaja-Kreisel sind die Bewegungsfunktionen mathematisch anspruchsvoll und fast alle seine Bewegungen ändern ihr Stabilitätsverhalten wenn sie schneller oder langsamer erfolgen. Der deutsche Mathematiker Wilhelm Hess entdeckte 1890 das loxodromische Pendel, dessen Schwerpunkt sich wie bei einem sphärischen Pendel unter kreiselspezifischer Schwerebeschleunigung bewegt.
Jeder Kreisel kann permanente Staude-Drehungen um eine körperfeste lotrechte Achse ausführen. Ebenfalls sind pseudoreguläre Präzessionen möglich, wenn der Drehimpuls groß und nahe einer Symmetrieachse ausgerichtet ist. Die Bewegung gleicht der regulären Präzession, bei der der Kreisel um eine raumfeste und eine andere körperfeste Achse gleichmäßig rotiert und die beiden Achsen einen gleichbleibenden Winkel einschließen. Bei der pseudoregulären Präzession treten jedoch mit dem Auge kaum wahrnehmbare, kleine, überlagernde, zykloidenähnliche Oszillationen der Drehachse auf, die nach einem der Astronomie entlehnten Wort ebenfalls Nutationen genannt werden[34][35].
Eine Zusammenstellung der wenigen Fälle, in denen bis Anfang des 21. Jahrhunderts exakte Lösungen der Bewegungsgleichungen gelungen sind, finden sich bei den Euler-Poisson-Gleichungen[36]. Die Energiefläche, auf der die Winkelgeschwindigkeit entlangfährt, kann bei allen Kreiseln analytisch beschrieben werden und es zeigt sich, dass die Fläche in relativen Gleichgewichten verzweigen kann, beispielsweise wenn der Kreisel die aufrechte Position passiert. In solchen Verzweigungspunkten ändert die Energiefläche ihre Eigenschaften (Topologie), was analytisch darstellbar und kreiseltheoretisch von Interesse ist.[22]
Kinematik von Kreiseln
Die Kinematik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die nicht von der Masse abhängen.
Bezugssysteme und Euler-Winkel
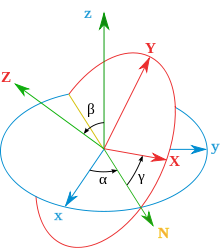
In der Kreiseltheorie werden vor allem zwei Bezugssysteme verwendet:
Im Inertialsystem (blau in Abb 4), in dem der Bezugspunkt ruht und der Kreisel rotiert, werden die Euler-Winkel definiert, die die Orientierung der Hauptachsen des Kreisels im Raum angeben. Der zeitliche Verlauf der Winkel bestimmt die Bewegungsfunktion des Kreisels. Im raumfesten System können die Massenträgheitsmomente um nicht festgehaltene Achsen zeitlich variabel sein.
Im mitrotierenden körperfesten Bezugssystem (rot) sind die Bewegungsgleichungen besonders leicht zu formulieren, weil dort die Trägheitsmomente zeitlich konstant sind. In den Bewegungsgleichungen müssen hier auftretende Trägheitskräfte berücksichtigt werden. Diese sind die Euler-Kraft und die Fliehkraft. Corioliskräfte kommen hier nicht vor, weil beim Starrkörper eine Bewegung seiner Massenpunkte relativ zum Körper ausgeschlossen ist.
In der Kreiseltheorie werden die Basisvektoren im raumfesten Bezugssystem mit den Euler’schen Winkeln in der Standard-x-Konvention (z, x', z") ausgedrückt, siehe Abb. 4. Der Winkel ψ ist der Präzessionswinkel, ϑ der Neigungswinkel und φ bestimmt die Eigendrehung des Kreisels. Bezeichnen die Einheitsvektoren êx,y,z die raumfeste Standardbasis (blau in Abb. 4) und êX,Y,Z = ê1,2,3 die mit dem Körper rotierende, bewegte Basis (rot in Abb. 4), dann lauten die mitbewegten Basiseinheitsvektoren bezüglich der raumfesten Basis:
Der Vektor
markiert die Knotenachse (gelbes N im Bild). Der Zusammenhang zwischen den Winkelgeschwindigkeiten und Vektoren ist
Häufig werden die Komponenten ω1,2,3 im Hauptachsensystem auch mit p, q und r bezeichnet und gelegentlich tauschen die Winkel ψ und φ die Bedeutung.
Bei sinϑ = 0 tritt eine Singularität auf, weil dann, wegen cosϑ = ±1, die Winkel ψ und φ in den Basisvektoren nach den Additionstheoremen nur als Kombination ψ ± φ vorkommen und somit verschiedene Winkel zur selben Basis führen können.
Euler’sche Geschwindigkeitsgleichung
Die Bewegungsfunktion starrer Körper ist durch die Euler’sche Geschwindigkeitsgleichung
gegeben. Sie gibt zur Zeit t für ein Partikel am Ort die Geschwindigkeit an, die sich aus der Bewegung eines Bezugspunkts und einer Drehung um ihn mit Winkelgeschwindigkeit zusammen setzt. Das Rechenzeichen „ד bildet das Kreuzprodukt und der Überpunkt bildet die Zeitableitung. Der Bezugspunkt kann in den Ursprung des Koordinatensystems gelegt werden und bei vernachlässigbarer Fortschreitbewegung gilt die Geschwindigkeitsverteilung
Alle Partikel des Kreisels, die sich auf der Drehachse befinden (für die ist ), ruhen solange sie das tun. Da die Drehachse nicht an die Partikel des Kreisels gebunden ist, kann sich die Drehachse relativ zum Kreisel bewegen, was eine wichtige Eigenschaft der Kreiselbewegung ist, die Präzession oder Nutation genannt wird.
Speziell für betraglich konstante, körperfeste Vektoren verschwindet die relative Zeitableitung und berechnen sich die Raten
Kinetik von Kreiseln
Die Theorie des Kreisels behandelt im Wesentlichen dessen Kinetik[26], die sich mit den von der Masse abhängenden Bewegungsgrößen und deren Beeinflussung durch Kräfte befasst.
Hauptträgheitsmomente, Hauptachsen und Trägheitstensor
Jeder Starrkörper besitzt drei ausgezeichnete Achsen, die Hauptachsen, die paarweise zueinander senkrecht sind oder orthogonalisierbar sind. Die Momente der Fliehkräfte gleichen sich bei der Drehung um die Hauptachsen genau aus, sodass sich der Kreisel gleichförmig um sie drehen kann. Eine von der Lage des Massenmittelpunkts abhängige statische Unwucht mit entsprechenden Kraftwirkungen in den Lagern ist dabei nicht ausgeschlossen.
Das Maß für den Widerstand des Kreisels gegen Rotationsänderungen sind seine Trägheitsmomente, die bei den Hauptachsen Hauptträgheitsmomente genannt und mit Θ1,2,3 oder A, B und C bezeichnet werden. Die Hauptträgheitsmomente sind die Eigenwerte und die Hauptachsen ê1,2,3 die dazugehörigen Eigenvektoren des Trägheitstensors, der in der Kreiseltheorie zumeist in der Hauptachsendarstellung mit Diagonalgestalt auftritt und beim rotierenden Kreisel eine vergleichbare Rolle übernimmt wie die Masse bei der Translation. Der Trägheitstensor bildet die Winkelgeschwindigkeit auf den Drehimpuls ab. Bei einem aus einzelnen Massenpunkten aufgebauten starren Körper berechnet sich der Trägheitstensor aus der Summe
Die erste Summe ist über alle Massenpunkte zu erstrecken, wobei deren Position relativ zum Bezugspunkt ist und mi deren Masse bedeutet. Die Vektoren ĝ1,2,3 sind eine beliebige Basis, das Rechenzeichen „·“ bildet das Skalarprodukt, „⊗“ das dyadische Produkt von Vektoren und 1 ist der Einheitstensor. Diese Darstellung des Kreisels mittels ihn aufbauender Massenpunkte wird auch im Folgenden noch benutzt.
Da die Positionen bei einer Rotation zeitabhängig sind, ist es der Trägheitstensor im Allgemeinen ebenfalls. Die Komponenten Θij sind konstant, wenn die Basisvektoren ĝi körperfest sind, ansonsten zumeist zeitabhängig. Die letzte Darstellung zeigt den Trägheitstensor in seiner Hauptachsendarstellung mit Hauptträgheitsmomenten Θi und Hauptachsen êi. Die Hauptachsen sind körperfest und drehen mit dem Kreisel mit. Der Trägheitstensor ist symmetrisch und positiv definit.
Alle Massenträgheitsmomente, Drehimpulse und Drehmomente werden in der Kreiseltheorie immer bezüglich des Stützpunkts oder des Massenmittelpunkts aufgestellt.
Drehimpuls und Rotationsenergie von Kreiseln
Bei einem wie oben aus einzelnen Massenpunkten aufgebauten starren Körper kann mit obiger Geschwindigkeitsverteilung und der BAC-CAB-Formel der Drehimpuls relativ zum Bezugspunkt als Summe berechnet werden:[37]
Darin ist der aktuelle Impuls des i-ten Massenpunkts. Ein Vergleich von mit zeigt, dass der Trägheitstensor für Drehungen eine vergleichbare Rolle wie die Masse für Translationsbewegungen spielt. Hier offenbart sich jedoch auch die Ursache dafür, dass die Kreiseltheorie sehr viel verwickelter ist als die Kinetik der Fortschreitbewegungen eines Starrkörpers, denn bei letzteren sind Impuls und Geschwindigkeit parallel, was bei Drehimpuls und Drehgeschwindigkeit im Allgemeinen nicht der Fall ist. Außerdem ist die Masse eine konstante Größe und der Trägheitstensor zumeist nicht, weshalb die Winkelgeschwindigkeit bei konstantem Drehimpuls zeitabhängig sein kann und umgekehrt.
Die Rotationsenergie des Kreisels ergibt sich mit voraus gehender Zerlegung in einzelne Massenpunkte, der Euler’schen Geschwindigkeitsgleichung und den Eigenschaften des Spatprodukts zu
Weil demnach das Skalarprodukt von Winkelgeschwindigkeit und Drehimpuls positiv ist, schließen sie einen spitzen Winkel ein. Die aktuelle Winkelgeschwindigkeit berührt überdies das zum Drehimpulsbetrag L gehörende Drallellipsoid, sodass
hält. Zum einen sind hieraus bei der Anordnung Θ1 < Θ2 < Θ3 der Hauptträgheitsmomente die Schranken
- oder
ersichtlich, denn der kleinste Klammerausdruck kann nicht positiv und der größte nicht negativ sein. Zum anderen zeigt sich beim Euler-Kreisel, dass der Polkegel, der aus den Punkten besteht, für die ist, einen Ellipsenkegel oder einen Kreiskegel darstellt[38], siehe Abb. 3.
Eulersche Kreiselgleichungen
Die Euler’schen Kreiselgleichungen ergeben sich aus dem Drallsatz . Die #Kreiselwirkung auf der rechten Seite steht für Trägheitseffekte im rotierenden Bezugssystem:[39]
siehe Drallsatz am starren Körper. Die Vektoren in den eckigen Klammern stellen in der mittleren Gleichung die Euler-Kraft und unten die Zentrifugalkraft am Massenpunkt mit Masse mi am Ort dar. Würde der Kreisel mit konstant gehaltener Winkelgeschwindigkeit um die instantane Drehachse kreisen, dann würden die Zentrifugalkräfte ein resultierendes Moment haben, das gerade der obigen Summe entspricht. Da bei der wirklichen Bewegung die Drehachse jedoch ihre Lage beständig ändert, hat Louis Poinsot für diese Zentrifugalkräfte den Namen fiktive Zentrifugalkräfte vorgeschlagen.[40]
In den Drallsatz eingesetzt entsteht mit den Kreiselwirkungen:[39]
Darin bildet die relative Zeitableitung im körperfesten Hauptachsensystem. Die Komponenten dieser Vektorgleichung sind im Hauptartikel nachzuschlagen.
Integrale der Bewegung
In der Kreiseltheorie werden bei der Rotation eines Kreisels unveränderliche physikalische Größen Integrale, manchmal auch erste Integrale genannt, englisch first integrals[15]. Diese sind von hervorragender Bedeutung, weil sie die Lösung der Kreiselgleichungen ermöglichen oder zumindest, wie das Jellett-Integral beim Spielkreisel, die Bewegungen klassifizieren.
Beim Euler-Kreisel ist und somit der Drehimpuls konstant. Der Drehimpuls, seine raumfesten Komponenten und sein Betrag sind bei dem Kreisel Integrale. Wenn das Schwerefeld konservativ ist, so wie das der Erde, befolgt die Kreiselbewegung den Energieerhaltungssatz, weshalb die Gesamtenergie dann ein Integral ist. Beim schweren Kreisel hat das Moment der lotrechten Schwerkraft keine Komponente in Lotrichtung und somit ist der Drehimpuls in dieser Richtung ein Integral. Jedoch besitzen die Integrale, wie beispielsweise die Kowalewskaja-Konstante, nicht immer eine anschauliche Bedeutung.
Lagrange- und Hamiltonfunktion des Kreisels
Die Lagrangefunktion des Kreisels ist die Differenz der Rotationsenergie und der potentiellen Energie
Darin sind jeweils für k=1,2,3
- Θk die Hauptträgheitsmomente,
- Lk die Drehimpulse,
- nk die Richtungskosinus des lotrecht nach oben weisenden Einheitsvektors und
- sk die Koordinaten des Massenmittelpunkts
im Hauptachsensystem.
Die Lagrange-Funktion kann mit den Euler-Winkeln ausgedrückt werden, deren zeitlicher Verlauf dann aus den Lagrangegleichungen resultieren.
Die Hamiltonfunktion H des Kreisels ist die Summe aus Rotationsenergie und der potentiellen Energie:
Die Euler-Poisson-Gleichungen können mit ihr und der Poisson-Klammer {} ausgedrückt werden:
- für i = 1, 2, 3
Diese Bewegungsgleichungen lassen sich auch in der Vektorform[41]
schreiben. Darin ist M der Koordinatenvektor des Drehimpulses und γ der Koordinatenvektor des Einheitsvektors in Richtung der Schwerebeschleunigung jeweils bezüglich des Hauptachsensystems.
Die Poisson Algebra e(3) dieser Variablen ist gegeben durch
Darin ist εijk das Levi-Civita-Symbol. Es gibt zwei Casimir Funktionen F1 = M · γ und F2 = γ², die bezüglich der Poisson-Klammer mit jeder Funktion von M und γ kommutieren und die auch gleichzeitig Integrale der Hamiltonfunktion sind.[42]
Fußnoten
- ↑ Grammel (1920), S. 2, Grammel (1950), S. 3.
- ↑ Grammel (1920), S. V, Grammel (1950), S. III, Magnus (1971), S. 1.
- ↑ Ludwig Darmstaedter (Hrsg.): Handbuch zur Geschichte der Naturwissenschaften und Technik. Springer-Verlag, Berlin, Heidelberg 1908, S. 209 (wikimedia.org [PDF; abgerufen am 19. Januar 2020]).
- ↑ Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 154, doi:10.1002/zamm.19640440402 (wiley.com).
- ↑ Leonhard Euler: Über die Bewegung der Rotation von starren Körpern um eine variable Achse. In: Königlich Preußische Akademie der Wissenschaften zu Berlin (Hrsg.): Mémoires de l’Académie des Sciences de Berlin. Band 14. Petersburg 1758, S. 173 und 190. (französisch, archive.org [abgerufen am 11. Januar 2020] Originaltitel: Du mouvement de rotation des corps solides autour d'un axe variable.).
- ↑ Joseph-Louis Lagrange: Mécanique Analytique. Tome Second. Corucier, Paris 1815, S. 265 f. (französisch, archive.org [abgerufen am 20. August 2017]). oder Joseph-Louis Lagrange: Analytische Mechanik. Vandenhoeck und Ruprecht, Göttingen 1797 (archive.org [abgerufen am 20. August 2017] Deutsche Übersetzung von Friedrich Murhard).
- ↑ Tuschmann und Hawig (1993), S. 123.
- ↑ Siméon Denis Poisson: Traité de Méchanique. 3. Auflage. 1 bis 6. J. G. Garnier, Brüssel 1838 (französisch, archive.org [abgerufen am 3. November 2019]).
- ↑ Tuschmann und Hawig (1993), S. 123., Audin (2008), S. 91.
- ↑ Tuschmann und Hawig (1993), S. 119.
- ↑ siehe Literatur und F. Klein, A. Sommerfeld: The Theory of the Top. Volume I. Introduction to the Kinematics and Kinetics of the Top. Volume I. Birkhäuser, Basel, Boston 2008, ISBN 978-0-8176-4720-9, S. vii ff., doi:10.1007/978-0-8176-4721-6 (englisch, springer.com – Originaltitel: Über die Theorie des Kreisels. Übersetzt von R. J. Nagem, G. Sandri, Das Vorwort des Übersetzers mit historischem Abriss gibt es hier online als pdf-Datei.).
- ↑ Édouard Husson: Forschung nach algebraischen Integralen in der Bewegung eines schweren Körpers um einen festen Punkt. In: Annales de la faculté des sciences de Toulouse 2e série. 1906, S. 73–152, doi:10.5802/afst.232 (französisch, numdam.org [PDF; abgerufen am 7. März 2018] Originaltitel: Recherche des intégrales algébriques dans le mouvement d’un solide pesant autour d’un point fixe. Auf Seite 74 wird ein erster Beweisversuch von Roger Liouville 1897 als fehlerhaft aufgedeckt)., siehe auch Audin (2008), S. 106.
- ↑ Leimanis (1965), S. 53 ff.
- ↑ Magnus (1971), S. 129.
- ↑ a b Gashenenko und Richter (2003), S. 2525.
- ↑ K. Magnus: Kreiselprobleme/ Gyrodynamics. Symposion Celerina, 20. Bis 23. August 1962 / Symposion Celerina, August 20–23, 1962. Hrsg.: Hans Ziegler. Springer Verlag, Berlin u. a. 1963, ISBN 978-3-662-12200-6, S. 7, doi:10.1007/978-3-662-12200-6 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Magnus (1971), S. 109.
- ↑ Gashenenko und Richter (2003), S. 2532 f.
- ↑ Magnus (1971), S. 1.
- ↑ Grammel (1920), S. 3, Grammel (1950), S. 2, Tuschmann und Hawig (1993), S. 121.
- ↑ Magnus (1971), S. 2f.
- ↑ a b Gashenenko und Richter (2003), S. 2526 f.
- ↑ Klein und Sommerfeld (1910), S. 762.
- ↑ Magnus (1971), S. 2 und S. 47, Grammel (1920), S. 43.
- ↑ Klein und Sommerfeld (1910), S. 764.
- ↑ a b Grammel (1920), S. 3
- ↑ Grammel (1920), S. 70.
- ↑ Klein und Sommerfeld (1910), S. 767 f.
- ↑ Grammel (1950), S. 261 f.
- ↑ Magnus (1971), S. 119
- ↑ Duden│Präzession. Duden online, abgerufen am 5. November 2017. sowie Duden│Nutation. Duden online, abgerufen am 8. März 2018.
- ↑ Vladimir I. Arnol’d: Mathematische Methoden der klassischen Mechanik. Springer-Verlag, Basel 1988, ISBN 978-3-0348-6670-5, S. 159, doi:10.1007/978-3-0348-6669-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 14. Februar 2018] russisch: Математическе методы классическоя механики. Moskau 1979. Übersetzt von Prof. Dr. Peter Möbius, TU Dresden).
- ↑ Magnus (1971), S. 27.
- ↑ Kuypers (2016), S. 215
- ↑ E. F. Autenrieth, Max Ensslin: Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure. Springer-Verlag, Berlin 1922, ISBN 978-3-642-98876-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 5. November 2017]).
- ↑ Magnus (1971), S. 108.
- ↑ Das dyadische Produkt ist mit drei beliebigen Vektoren definiert durch
- ↑ Leimanis (1965), S. 11.
- ↑ a b In der Tensoralgebra kann auf Klammerungen verzichtet werden:
- ↑ Felix Klein, Conr. Müller: Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Mechanik. Hrsg.: Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien. Vierter Band, 1. Teilband. Springer Verlag, 2013, ISBN 978-3-663-16021-2, S. 586, doi:10.1007/978-3-663-16021-2 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 24. Januar 2020] siehe auch wikisource).
- ↑
Die Fréchet-Ableitung einer skalaren Funktion nach einem Vektor
ist der Vektor für den - sofern er existiert - gilt:
- ↑ Borisov und Mamaev (2001), S. 254.
Literatur
- R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 573533210 (archive.org – "Schwung" bedeutet Drehimpuls, "Drehstoß" etwa Drehmoment und "Drehwucht" Rotationsenergie, siehe S. VII).
oder
R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Erster Band: Die Theorie des Kreisels. Springer Verlag, Berlin u. a. 1950, ISBN 978-3-662-24311-4, doi:10.1007/978-3-662-26425-6 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 19. Januar 2020]). - K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. v (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 19. Januar 2020]).
- Wilderich Tuschmann, Peter Hawig: Sofia Kowalewskaja. Ein Leben für Mathematik und Emanzipation. Birkhäuser Verlag, Basel 1993, ISBN 978-3-0348-5721-5, doi:10.1007/978-3-0348-5720-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Mai 2017]).
- F. Klein, A. Sommerfeld: Über die Theorie des Kreisels. Heft I-III. Teubner, Leipzig 1897 (archive.org [abgerufen am 17. Januar 2020]).
Sowie
F. Klein, A. Sommerfeld: Über die Theorie des Kreisels. Heft IV. Teubner, Leipzig 1910 (archive.org [abgerufen am 17. Januar 2020]). - Friedhelm Kuypers: Klassische Mechanik. Wiley-VCH, Weinheim 2016, ISBN 978-3-527-33960-0 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 7. November 2017]).
- Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 10 f., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).
- I. G. Gashenenko, P. H. Richter: Enveloping Surfaces And Admissible Velocities Of Heavy Rigid Bodies. In: World Scientific Publishing Company (Hrsg.): International Journal of Bifurcation and Chaos. Band 14, Nr. 8, 2004, ISSN 0218-1274, S. 2525–2553, doi:10.1142/S021812740401103X (iamm.su [PDF; abgerufen am 2. Juni 2019] siehe S. 2537).
- A. V. Borisov, I. S. Mamaev: Euler-Poisson Equations and Integrable Cases. 2001, doi:10.1070/RD2001v006n03ABEH000176, arxiv:nlin/0502030 (englisch, Enthält Lösungen der Kreiselgleichungen, deren ausführliche Beschreibung und weiter führende Literaturangaben.).
- E. F. Autenrieth, Max Ensslin: Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure. Springer-Verlag, Berlin 1922, ISBN 978-3-642-98876-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 5. November 2017]).
- Michèle Audin: Erinnerungen an Sofja Kowalewskaja. Springer Verlag, London u. a. 2008, ISBN 978-0-85729-928-4, S. 106, doi:10.1007/978-0-85729-929-1 (englisch, eingeschränkte Vorschau in der Google-Buchsuche – Originaltitel: Remembering Sofya Kovalevskaya.).
Weblinks
- TIB AV-Portal der Technische Informationsbibliothek, qualitätsgeprüfte wissenschaftliche Videos zum Thema Kreisel.













![{\displaystyle {\begin{aligned}\mathbf {\Theta } :=&\sum _{i}m_{i}[({\vec {r}}_{i}\cdot {\vec {r}}_{i})\mathbf {1} -{\vec {r}}_{i}\otimes {\vec {r}}_{i}]\\=&\sum _{i,j=1}^{3}\Theta _{ij}{\hat {g}}_{i}\otimes {\hat {g}}_{j}=\sum _{i=1}^{3}\Theta _{i}{\hat {e}}_{i}\otimes {\hat {e}}_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69d8ce3d1800fcb1bacaeac5be18084ab49215fd)











![{\displaystyle {\begin{aligned}{\vec {K}}=&{\vec {K}}_{\text{Euler}}+{\vec {K}}_{\text{Zentrifugal}}\\{\vec {K}}_{\text{Euler}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\dot {\vec {\omega }}}\times {\vec {r}}_{i}]=-\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}\\{\vec {K}}_{\text{Zentrifugal}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}_{i})]=-{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ac4da65fd9d60da2085b9523d9d6cf3f2e88090)
















