Alpha-stabile Verteilungen
Die Familie der α-stabilen Verteilungen ist eine Verteilungsklasse von stetigen Wahrscheinlichkeitsverteilungen aus der Stochastik, die durch folgende definierende Eigenschaft beschrieben werden: sind unabhängige, identisch verteilte Zufallsvariablen, und gilt für die Summe
- für alle und eine Folge ,
so nennt man stabil verteilt, wobei als „hat dieselbe Verteilung wie“ zu lesen ist. Man kann zeigen, dass die einzig mögliche Wahl ist. Die reelle Zahl nennt man hierbei den Formparameter. Da die Theorie der stabilen Verteilungen maßgeblich durch Paul Lévy mitgestaltet wurde, nennt man jene Verteilungen deshalb auch manchmal Lévy-stabile Verteilungen.
Beispiele[Bearbeiten | Quelltext bearbeiten]
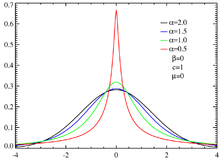
Obwohl die stabilen Verteilungen für jedes des obigen Intervalls wohldefiniert sind, ist nur für wenige spezielle Werte von α die Dichte explizit gegeben:
- Die Normalverteilung mit Erwartungswert 0 ist stabil mit Formparameter , denn bekanntlich gilt
- . Die Normalverteilung ist die einzige Verteilung mit dem Formparameter .
- Die zentrierte Cauchy-Verteilung erfüllt die Gleichung
- sie ist also stabil mit Formparameter .
- Die (eigentliche) Standard-Lévy-Verteilung ist stabil mit .
Eigenschaften[Bearbeiten | Quelltext bearbeiten]

- Die charakteristische Funktion einer α-stabilen Verteilung ist durch
- gegeben[1][2] Der Parameter heißt charakteristischer Exponent. Der Parameter heißt Schiefeparameter. Der Parameter ist positiv. Der Parameter ist ein Lageparameter.
- Endliche Varianz existiert nur für . Dies folgt unmittelbar aus dem zentralen Grenzwertsatz. Für spezialisiert sich die charakteristische Funktion zu ; dies ist charakteristische Funktion einer Normalverteilung mit dem Erwartungswert und der Varianz .
- Für hat die Verteilung den Erwartungswert , für existiert kein Erwartungswert. Dies folgt mit dem Gesetz der großen Zahlen.
- Alle α-stabilen Verteilungen sind unendlich teilbar und selbstähnlich („selfdecomposable“).
Analoge Konzepte für diskrete Verteilungen[Bearbeiten | Quelltext bearbeiten]
Für diskrete Verteilungen gibt es den Begriff der diskret-stabilen Verteilung[3][4], ein Beispiel einer solchen Verteilung ist die Poisson-Verteilung, welche bei diskret-stabilen Verteilungen einen ähnlichen Stellenwert einnimmt, wie die Normalverteilung bei Lévy-stabilen kontinuierlichen Dichten[5].
Literatur[Bearbeiten | Quelltext bearbeiten]
- Achim Klenke: Wahrscheinlichkeitstheorie. 2. Auflage. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76317-8, Kap. 16.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Paul Embrechts, Thomas Mikosch, Claudia Klüppelberg: Modelling extremal events (= Stochastic Modelling and Applied Probability. Band 33). Springer-Verlag, Berlin / Heidelberg / New York 1997, ISBN 3-540-60931-8, Theorem 2.2.3, S. 71, doi:10.1007/978-3-642-33483-2.
- ↑ Rick Durrett: Probability: Theory and Examples. 4. Auflage. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76539-8, S. 141.
- ↑ F. W. Steutel, K. van Harn: Discrete analogues of self-decomposability and stability. In: The Annals of Probability. Band 7, Nr. 3, S. 893–899, doi:10.1214/aop/1176994950.
- ↑ Luc Devroye: A triptych of discrete distributions related to the stable law. In: Statistics and Probability Letters. Band 18, Nr. 5, S. 349–351, doi:10.1016/0167-7152(93)90027-G.
- ↑ Stochastic Population Processes Analysis, Approximations, Simulations, Eric Renshaw, 2015, ISBN 9780191060397, Seite 134, https://books.google.de/books?id=pqE1CgAAQBAJ&pg=PA134






![{\displaystyle c_{n}=n^{1/\alpha },\alpha \in (0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbdeb876f39ae54ce5454e67f61cac8f99e2ff6b)










![{\displaystyle \psi _{\alpha ,\beta ,c,\mu }(t)={\begin{cases}\exp \left(i\mu t-c|t|^{\alpha }\left(1-i\beta \tan \left({\frac {\pi \alpha }{2}}\right)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha \in (0,1)\cup (1,2]\\\exp \left(i\mu t-c|t|\left(1+i\beta {\frac {2}{\pi }}\ln(|t|)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha =1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f1016b2295f9bb1580715e00912bc45730f9061)
![{\displaystyle \alpha \in (0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98dade01a06507996c8330ec68b7c0f7bc305a05)
![{\displaystyle \beta \in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88346c1460c3477cc60acc78f4c9742e51770644)






