Euler-Kreisel

Der kräftefreie Kreisel ist in der Kreiseltheorie ein Kreisel, auf den keine äußeren Kräfte wirken. Die Bewegungsgleichungen konnte erstmals Leonhard Euler 1758 lösen[1], zu dessen Ehren der Kreisel auch Euler-Kreisel genannt wird.
Die bestimmenden Gleichungen sind die Euler-Poisson-Gleichungen, deren Lösungen nur hier, beim Lagrange-Kreisel und dem Kowalewskaja-Kreisel bei beliebigen Anfangsbedingungen eindeutige Funktionen der Zeit und mit algebraischen Integralen ableitbar sind.[2]
Die Winkelgeschwindigkeiten lassen sich mit den Jacobi'schen elliptischen Funktionen ausdrücken, die beim symmetrischen Kreisel in den Sinus und Kosinus übergehen. Hier zeigt der Kreisel besonders regelmäßiges und anschauliches Verhalten, siehe #Beschreibung der Bewegung. Die Poinsotsche Konstruktion führt die Bewegung auf das Abrollen des Energieellipsoids auf einer Ebene zurück.
Außer in der Schwerelosigkeit kann ein kräftefreier Kreisel in einem Schwerefeld realisiert werden, indem er in seinem Schwerpunkt drehbar, beispielsweise wie in Abb. 1 kardanisch aufgehängt wird. Der eulersche Kreisel findet z. B. in Kreiselkompassen und gyroskopischen Steuersystemen technische Anwendung.
Bezeichnungen[Bearbeiten | Quelltext bearbeiten]
Die Bewegungen des kräftefreien Kreisels heißen in der Kreiseltechnik Nutation[3]. Die azimutale Drehung wird auch Präzession genannt[4]. Weitere Bezeichnungen sind in den Hauptartikeln aufgeführt.
Allgemeine Eigenschaften der Bewegung kräftefreier Kreisel[Bearbeiten | Quelltext bearbeiten]
Kreiselgleichungen[Bearbeiten | Quelltext bearbeiten]
Die Bewegungsfunktion des Kreisels bestimmt sich mit den von Leonhard Euler aufgestellten Kreiselgleichungen, die, wenn der Massenmittelpunkt im Stützpunkt liegt, inhaltsgleich zu den Euler-Poisson-Gleichungen für den schweren Kreisel sind. Die Gleichungen beziehen sich auf das mit dem Körper rotierende Hauptachsensystem und bilden das autonome gewöhnliche Differentialgleichungssystem
Darin sind jeweils für k=1,2,3
- Θk die Hauptträgheitsmomente,
- Lk = Θkωk die Drehimpulse und
- ωk die Winkelgeschwindigkeiten
im Hauptachsensystem. Der Überpunkt bildet die Zeitableitung.
Auf der linken Seite steht die Kreiselwirkung der Euler-Kräfte und auf der rechten Seite diejenige der Fliehkräfte, siehe Drallsatz am Starren Körper. Die Euler-Kräfte sind Ausdruck von Winkelbeschleunigungen, die hier von den Fliehkräften im Kreisel hervor gerufen werden. Umgekehrt führen die Winkelbeschleunigungen zur Änderung der Drehachse und Drehgeschwindigkeit, was die Fliehkräfte beeinflusst. Folge dieses dynamischen Wechselspiels ist die Nutation des kräftefreien Kreisels.
Integrale der Bewegung[Bearbeiten | Quelltext bearbeiten]
Die Drehbewegung eines kräftefreien Kreisels unterliegt neben den Kreiselgleichungen noch zwei Bedingungen.
Zum einen erzwingt die Drehimpulserhaltung im raumfesten xyz-System, dass alle drei Drehimpulskomponenten von
im kräftefreien Fall konstant sind. Als zweite Bedingung bleibt die Rotationsenergie Erot gemäß dem Energieerhaltungssatz erhalten.
Im lokalen körperfesten Hauptachsensystem heißt das:
Die Erhaltung von Lx,y,z, L² und Erot ist im Einklang mit obigen Kreiselgleichungen, was durch Zeitableitung der Konstanten und Einsetzen der Kreiselgleichungen und der Euler-Winkel der Kreiseltheorie nachgewiesen werden kann. Die Konstanten der Bewegung werden in der Kreiseltheorie Integrale genannt.[5]
Obige Gleichungen definieren Ellipsoide. Die mit den Winkelgeschwindigkeiten ausgedrückten Gleichungsteile stellen in der oberen Gleichung das Drallellipsoid und in der unteren das Energieellipsoid dar. Die mit dem Drehimpuls ausgedrückten Flächen sind in der oberen Gleichung die Drallkugel und in der unteren das MacCullagh-Ellipsoid. Die Winkelgeschwindigkeiten und Drehimpulse sind jeweils Teil beider Flächen.
Die Drallkugel und das MacCullagh-Ellipsoid haben nur dann gemeinsame Punkte, wenn die Schranken für Drehimpuls und Rotationsenergie eingehalten werden[6]. Multiplikation von 2Erot mit -L² und L² mit 2Erot und Addition liefert:
Die Gleichung für den Polkegel, der aus den Punkten besteht, für die ist, ergibt sich hieraus zu[7]:
Beim unsymmetrischen Euler-Kreisel stellt das einen Ellipsenkegel und beim symmetrischen einen Kreiskegel dar, siehe #Beschreibung der Bewegung.
MacCullaghs Deutung der Kreiselbewegung[Bearbeiten | Quelltext bearbeiten]

Von James MacCullagh stammt eine geometrische Deutung der Kreiselbewegung, die wie die Poinsot’sche Konstruktion anschaulich aber nicht so fruchtbar ist wie letztere[8]. Der Drehimpuls ist im raumfesten System konstant, bildet die invariable Gerade durch den Stützpunkt und berührt jederzeit das MacCullagh-Ellipsoid, das im körperfesten System aus den Endpunkten aller Drehimpulse besteht, die zur aktuellen Rotationsenergie führen, siehe Abb. 3. Das MacCullagh-Ellipsoid bewegt sich mit dem Kreisel derart, dass der Drehimpuls gleichzeitig auf dem Ellipsoid und der Drallkugel ist, wobei die rot gezeichneten Drallpolkurven entstehen. Die Punkte auf den Drallpolkurven haben somit alle denselben Abstand zum Stützpunkt. Das Lot des Stützpunkts auf die Tangentialebene an das MacCullagh-Ellipsoid im Endpunkt des Drehimpulses ist parallel zur aktuellen Winkelgeschwindigkeit. Besagte Tangentialebene ist, anders als die invariable Ebene der Poinsot’schen Konstruktion, nicht raumfest.
Das Kreuzprodukt aus Winkelgeschwindigkeit und Drehimpuls ist umgekehrt gleich der Kreiselwirkung der Fliehkräfte, der genau entgegengesetzt die Kreiselwirkung der Euler-Kräfte ist, die Ausdruck von Änderungen der Drehgeschwindigkeit und -achse, also der Ausrichtung des MacCullagh-Ellipsoids, sind, siehe auch #Kreiselgleichungen.
Stabilitätsbetrachtungen[Bearbeiten | Quelltext bearbeiten]

In Abb. 4 ist die Drallkugel und zu verschiedenen Rotationsenergien gehörende Drallpolkurven aus drei Richtungen gesehen gezeichnet. Die Drallpolkurven sind geschlossene Kurven (rot und blau im Bild), die Kreis-, Ellipsen- oder Taco-förmig sein können und wie das MacCullagh-Ellipsoid symmetrisch zu den von den Hauptachsen aufgespannten Ebenen sind. Auf den blauen Kurven finden perizykloidische Bewegungen statt während auf den roten Kurven die Bewegung epizykloidisch genannt wird, siehe Poinsot’sche Konstruktion. Dazwischen befindet sich die Separatrix, die diese beiden Bewegungsformen voneinander trennt.
Liegt der Drehimpuls in der Nähe der Hauptträgheitsachse mit dem größten oder dem kleinsten Trägheitsmoment (blaue bzw. rote Punkte in Abb. 4), dann verbleibt er auch in dessen Nähe, denn diese Punkte werden von den Drallpolkurven umringt. Deshalb sind diese Drehachsen stabile Drehachsen freier Drehungen. Ihre Schnittpunkte mit der Drallkugel sind elliptische Fixpunkte einer autonomen Differentialgleichung.
Aus den Achsverhältnissen der Ellipsen kann ein Maß für die Stabilität der Drehachsen abgeleitet werden, siehe Stabilitätsbetrachtungen bei der Poinsot’schen Konstruktion.
Liegt der Drehimpuls genau auf der 2-Achse (schwarzer Punkt), dann verbleibt er dort, andernfalls entfernt er sich vom Schnittpunkt, denn dieser wird nicht von den Drallpolkurven umkreist. Die 2-Achse ist eine instabile Drehachse, sie trifft das MacCullagh-Ellipsoid in einem hyperbolischen Fixpunkt oder Sattelpunkt der zugehörigen autonomen Differentialgleichung (siehe auch #Stabilität der Bewegung unsymmetrischer Kreisel weiter unten). Die Bewegung auf der Separatrix ist instabil, denn bei der kleinsten Störung wird die Bahn epi- oder perizykloidisch.
Wenn die Hauptträgheitsmomente Θ1,2 übereinstimmen, womit der Kreisel ein symmetrischer Kreisel wird, dann ist das MacCullagh-Ellipsoid ein Rotationsellipsoid um die 3-Achse, die Separatrix wird zu einem Großkreis in der 1-2-Ebene und die Drallpolkurven sind Kleinkreise parallel zu dieser. Die Drehung um die Figurenachse (Symmetrieachse 3) ist jedenfalls stabil, denn die Drallpolkurven umringen als Kleinkreise diese Achse. Die zur Figurenachse senkrechten, äquatorialen Hauptachsen weisen komplexes Stabilitätsverhalten auf:
- Bezüglich der Winkelgeschwindigkeiten und des Neigungswinkels ϑ sind Drehungen um eine äquatoriale Achse stabil,
- Bezüglich der Winkel ψ und φ und den Winkelgeschwindigkeiten ω1,2 sind Drehungen um eine äquatoriale Achse instabil.
Denn bei Störung der Drehung um die 1-Achse mittels einer kleinen Winkelgeschwindigkeit um die 3-Achse wird die Drallpolkurve zu einem Kleinkreis um die 3-Achse und die Drehachse umläuft parallel zur 1-2-Ebene die Figurenachse. Sie bleibt also nicht in der Nähe der 1-Achse was Instabilität von ω1 bezüglich Störung von ω3 bedeutet. Eine kleine Störung der axialen Winkelgeschwindigkeit ω3 oder des Neigungswinkels ϑ führt jedoch zu einer klein bleibenden Veränderung. In gleicher Weise werden die anderen Größen auf Stabilität gegenüber Störungen untersucht[9].
Zur Stabilität des Kugelkreisels, siehe dort.
Die Bewegungen des Drehimpulses im lokalen Bezugssystem[Bearbeiten | Quelltext bearbeiten]
Der Drehimpuls durchwandert die in Abb. 3 und Abb. 4 gezeichneten Drallpolkurven ohne jemals stillzustehen oder gar die Umlaufrichtung zu wechseln. Denn abseits der Hauptträgheitsachsen verschwindet höchstens eine Komponente des Drehimpulses und daher können die lokalen Geschwindigkeiten den Kreiselgleichungen zufolge nicht alle drei auf einmal null sein.
Mangels äußerer Einwirkungen macht der kräfefreie Kreisel keine Sprünge. Die lokalen Komponenten des Drehimpulses sind somit Lipschitz-stetig und daher können sich die Trajektorien des Drehimpulses nach dem Satz von Picard-Lindelöf nicht schneiden. Diese Bedingung ist auf der Separatrix verletzt (in Abb. 4 schwarz gestrichelt). Auf ihr bildet sich daher eine aperiodische Bewegung aus, denn der Drehimpuls kann die Schnittpunkte auf der 2-Achse nicht überschreiten. Die Hauptträgheitsachse mit dem mittleren Hauptträgheitsmoment nähert sich auf einer Loxodrome asymptotisch der vom Drehimpuls gegebenen Achse, siehe #Bewegung auf der Separatrix unten.
Wenn die Rotationsenergie abnimmt, beispielsweise durch Dissipation, wird die Drehachse in Richtung der Achse mit dem größten Trägheitsmoment wandern, was in Abb. 4 die 3-Achse ist, denn dort berührt das MacCullagh-Ellipsoid mit der kleinsten Energie die Drallkugel.
Kräftefreier symmetrischer Kreisel[Bearbeiten | Quelltext bearbeiten]
Beim symmetrischen Kreisel sind per definitionem zwei der drei Hauptträgheitsmomente gleich. Die Bewegung ist eine regelmäßige und anschauliche Reguläre Präzession. Ohne Beschränkung der Allgemeinheit wird hier von Θ1=Θ2=:Θ0 und Drehung um die 3-Achse – der Figurenachse – ausgegangen.
Beschreibung der Bewegung[Bearbeiten | Quelltext bearbeiten]
Beim symmetrischen Kreisel vereinfacht sich die dritte Kreiselgleichung im kräftefreien Fall zu , sodass die Winkelgeschwindigkeit ω3 und somit auch der Drehimpuls L3 konstant sind. Die zwei anderen Kreiselgleichungen bilden das lineare gewöhnliche Differentialgleichungssystem
mit konstantem Koeffizient . Zeitableitung der Gleichungen führt auf zwei entkoppelte Differentialgleichungen , deren allgemeine Lösung wie folgt darstellbar ist:
Die Werte ω1,2(0) sind Anfangsbedingungen zur Zeit t = 0 und werden durch eine 2 × 2 Drehmatrix auf die aktuellen Werte abgebildet. Falls ω3(0) = 0 und/oder ω1(0) = ω2(0) = 0 gilt, so bleiben ω1 und ω2 konstant und der Kreisel führt eine konstante Drehbewegung aus oder bleibt im Spezialfall ω1,2,3(0) = 0 in Ruhe.

Für die Skizzierung der allgemeinen Bewegung wird im Massenmittelpunkt des Kreisels zum Zeitpunkt t = 0 ein kartesisches Koordinatensystem mit x-, y- und z-Achse so gelegt, dass die Figurenachse und die Winkelgeschwindigkeit in der xz-Ebene liegen, siehe Abb. 5. Das Hauptachsensystem sei anfänglich so ausgerichtet, dass die Winkelgeschwindigkeit und die Figurenachse in der 13-Ebene liegen und einen Winkel λ einschließen (in Abb. 5 anders dargestellt). Dann ist ω1(0) = ω sin(λ), ω2(0) = 0 und ω3(0) = ω cos(λ) mit dem Betrag der Winkelgeschwindigkeit. Die Hauptachsen werden wie bei den Euler-Winkeln in der Kreiseltheorie eingeführt mit ê1,2,3 bezeichnet.
Die oben angegebene Lösung der Kreiselgleichungen ergibt mit den getroffenen Anfangsbedingungen:
Der Differenzvektor hat den konstanten Betrag und rotiert um die Figurenachse mit der Drehzahl . Die Figurenachse und die Winkelgeschwindigkeit schließen daher immer denselben Winkel, nämlich λ, ein. Die Winkelgeschwindigkeit führt im körperfesten Hauptachsensystem eine Drehbewegung um die Figurenachse aus und formt dabei den körperfesten Polkegel mit dem halben Öffnungswinkel λ (rot in Abb. 5 und Abb. 6).
Im raumfesten System ist der Drehimpuls
um den Massenmittelpunkt konstant (grün in Abb. 5) und bildet die Präzessionsachse[10]. An letzterer Zerlegung ist erkennbar, dass der Drehimpuls in der von der Figurenachse und der Winkelgeschwindigkeit aufgespannten Ebene, der Präzessionsebene[10], liegt. Die Figurenachse und die Winkelgeschwindigkeit drehen gemeinsam um die raumfeste Präzessionsachse.
Das Koordinatensystem kann nun – wie in Abb. 5 – so ausgerichtet werden, dass der Drehimpuls in z-Richtung weist und somit gilt. Weil sich die Rotationsenergie
ebenfalls nicht ändert, ist auch die z-Komponente ωz der Winkelgeschwindigkeit in Richtung des Drehimpulses konstant. Damit bewegt sich die Winkelgeschwindigkeit auch um die raumfeste z-Richtung auf einem Kegel, dem raumfesten Spurkegel (blau in Abb. 5 und Abb. 6, dort „raumfester Gangpolkegel“ genannt).

Der Gangpolkegel rollt auf dem Rastpolkegel ab. Beim prolaten (gestreckten) Kreisel ist Θ0 > Θ3 und der Gangpolkegel rollt wie in Abb. 5 außen auf dem Rastpolkegel ab. Beim oblaten (abgeplatteten) Kreisel ist Θ3 > Θ0 und der Gangpolkegel rollt wie in Abb. 6 innen auf dem Rastpolkegel ab.
Das Abrollen ist schlupflos, denn die gemeinsame Mantellinie von Rastpol- und Gangpolkegel ist die von der Winkelgeschwindigkeit gestellte momentane Drehachse, die durch den ruhenden Massenmittelpunkt geht (in Abb. 6 anders dargestellt). Die Partikel des Kreisels auf der Drehachse stehen still solange sie das tun, der Rastpolkegel ruht sowieso, und Schlupf zwischen Gang- und Rastpolkegel ist mithin ausgeschlossen.
Der Winkel ϑ zwischen der Figurenachse und dem Drehimpuls sowie die z-Komponente ωz der Winkelgeschwindigkeit können mit der mechanischen Analyse im folgenden Abschnitt ermittelt werden.
Bewegungsfunktion des symmetrischen Kreisels[Bearbeiten | Quelltext bearbeiten]
Wenn, wie im vorherigen Abschnitt, der Drehimpuls in Richtung der z-Achse weist und die Winkelgeschwindigkeit ω sowie der Winkel λ vorgegeben werden (alle diese Größen sind Konstanten der Bewegung), dann berechnen sich der Drehimpuls
die Winkelgeschwindigkeiten
und die Winkel
in Radiant. Die Funktion tan ist der Tangens und arctan seine Arkusfunktion. Die von der Figurenachse und der Winkelgeschwindigkeit aufgespannte Präzessionsebene, in der auch den Drehimpuls liegt, schließt mit der xz-Ebene den Winkel
ein.
| Beweis |
| Der Drehimpuls ist in Abwesenheit äußerer Momente konstant und weise in einem raumfesten kartesischen xyz-Koordinatensystem in z-Richtung. Dann ergibt sich mit den Euler-Winkeln in der Kreiseltheorie:
Die Winkelgeschwindigkeit ω3 ist den Kreiselgleichungen zufolge genauso wie der Drehimpuls L und konstant, weshalb auch der Winkel ϑ konstant ist. Daraus folgt Mit den Kreiselgleichungen und den Zusammenhängen zwischen den Winkelgeschwindigkeiten und den Winkeln zeigt sich Bei findet keine Drehung statt (wegen L = 0) und bei sin(ϑ) = 0 dreht der Kreisel gleichförmig um seine Figurenachse. Ansonsten ergibt sich Die z-Komponente ωz der Winkelgeschwindigkeit lautet |
| Anfangsbedingungen |
|---|
| Zur Zeit t = 0 ist und diesen Wert behält ω3. Der Winkel ϑ kann nun als Funktion des Winkels λ ausgedrückt werden:
Der Kotangens cot ist der Kehrwert des Tangens. Wegen und folgt für den Drehimpuls: Die Vorgaben können mit dem Anfangswert für den Winkel φ erfüllt werden, sodass . Die Winkelgeschwindigkeit lautet mit den Additionstheoremen zur Zeit t = 0: Damit diese in der xz-Ebene liegt, wird der Anfangswert von ψ auf gesetzt, sodass sich ergibt. Wenn der Drehwinkel der Präzessionsebene um die z-Achse mit µ bezeichnet wird und zu Beginn den Wert null hat, dann folgt mit obigem ωz und tan(ϑ), sowie ω3 = ω cos(λ): |
Kräftefreier asymmetrischer Kreisel[Bearbeiten | Quelltext bearbeiten]
Asymmetrische Kreisel besitzen per definitionem drei verschiedene Hauptträgheitsmomente. Dreht sich ein solcher Kreisel um die 3-Achse, dann kann diese Bewegung instabil oder stabil sein. Im ersteren Fall nehmen kleine Störungen exponentiell zu und der Kreisel beginnt zu taumeln, was im nächsten Abschnitt begründet wird. Im stabilen Fall bilden sich periodische Bewegungsformen des zweiten Abschnitts aus. Über den Spezialfall der Bewegung auf der Separatrix, die im Abschnitt #Stabilitätsbetrachtungen definiert wurde, wird am Schluss informiert.
Stabilität der Bewegung unsymmetrischer Kreisel[Bearbeiten | Quelltext bearbeiten]
Die Hauptachsen mit dem größten oder dem kleinsten Hauptträgheitsmoment sind stabile Drehachsen. Dies ist spätestens seit 1851 bekannt[11] und mit einem rotierend in die Höhe geworfenen Tischtennisschläger auch leicht zu demonstrieren. Im Englischen ist die Aussage entsprechend als „Satz vom Tennisschläger“ (tennis racket theorem)[12] geläufig. Nachdem der sowjetische Kosmonaut Wladimir Dschanibekow während eines Raumfluges 1985 die Bewegung eines Bauteils um seine instabile Hauptträgheitsachse beobachtet hat, wurde der Sachverhalt genauer untersucht[13] und wird seitdem gelegentlich „Dschanibekow-Effekt“ genannt.
Um die Stabilität der Drehachsen zu prüfen, soll der Kreisel zunächst vor allem um die 3-Achse rotieren: und . Nun lauten die Kreiselgleichungen
Wie im Abschnitt #Beschreibung der Bewegung entsteht durch Ableitungen nach der Zeit und mit der näherungsweisen Konstanz der Winkelgeschwindigkeit ω3:
Falls k negativ ist, kommt es zu positiver Rückkopplung der Winkelgeschwindigkeiten und damit zum Verlassen der Rotation um die 3-Achse hin zu einem Taumeln. Falls k positiv ist, ergeben sich periodische Bewegungsformen um die 3-Achse. Dafür müssen die Hauptträgheitsmomente Θ1,2 entweder beide größer oder beide kleiner als das dritte Hauptträgheitsmoment Θ3 sein, woraus die obige Aussage über die Stabilität der Achsen folgt.
Bei sehr unterschiedlichen Hauptträgheitmomenten kann auch eine stabile Drehachse instabil erscheinen. Die Poinsot’sche Konstruktion gibt ein geometrisches Stabilitätskriterium für die Hauptträgheitsachsen, das diesem Phänomen gerecht wird.
Bewegungsfunktion des asymmetrischen Kreisels[Bearbeiten | Quelltext bearbeiten]
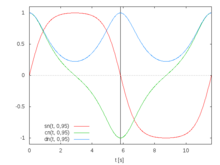
Beim asymmetrischen Kreisel können die Kreiselgleichungen im kräftefreien Fall mit den Jacobi’schen elliptischen Funktionen sn, cn und dn erfüllt werden[14]. Dazu werden die Hauptachsen so nummeriert, dass Θ1 > Θ2 > Θ3 wird. Aus der Rotationsenergie und dem Betragsquadrat des Drehimpulses
ergeben sich bei epizykloidischen Bewegungen, wo L² < 2Θ2Erot ist, die Winkelgeschwindigkeiten
mit der Frequenz a und dem elliptischen Modul k
Bei perizykloidischen Bewegungen ist L² > 2Θ2Erot und
mit der Frequenz a und dem elliptischen Modul k
Von den Wurzeln bei den Winkelgeschwindigkeiten haben immer zwei gleiches Vorzeichen und es müssen verschiedene Vorzeichen vorkommen, was insgesamt sechs mögliche Kombinationen erlaubt, von denen hier eine willkürlich ausgewählt wurde.
Die in der Kreiseltheorie benutzten eulerschen Winkel berechnen sich aus[15]
Anders als beim kräftefreien symmetrischen Kreisel sind die Winkelgeschwindigkeiten und der Winkel ϑ zwischen dem Drehimpuls und der 3-Achse nicht konstant.
Die Funktionen sn und cn sind periodisch mit der Periode 4K und dn mit der Periode 2K, siehe Abb. 8, wo K das vollständige elliptische Integral erster Art ist:
Die Winkelgeschwindigkeiten ω1,2,3 sind somit periodisch mit der Periodenlänge ; nach dieser Zeit kehren sie wieder in ihren Ausgangszustand zurück: ω1,2,3(t+T) = ω1,2,3(t). Aus der Periodizität von folgt Nach der Zeit T ist der Kreisel also in einer um Δψ verdrehten Position. Der Kreisel kehrt nur dann in die Ausgangsposition zurück, wenn Δψ/π eine rationale Zahl ist.[16]
Die Formeln sind auch für symmetrische Kreisel gültig. Allerdings können gestreckte Kreisel mit Θ1 = Θ2 > Θ3 nur epizykloidische und abgeplattete mit Θ1 > Θ2 = Θ3 nur perizykloidische Drehungen ausführen, da sonst die Amplitude von ω2 über alle Grenzen wächst. Bei den erlaubten Bewegungen ist k = 0, sodass die elliptischen Funktionen sn und cn zu den harmonischen Funktionen sin bzw. cos werden und dn ≡ 1 ist. Dann geht die hiesige Lösung in die des symmetrischen Kreisels über.
Ausgenommen hiervon sind einzig kräftefreie Kugelkreisel, wo L² - 2Θ3Erot = 2Θ1Erot - L² = 0 ist und die Amplituden nicht mehr definiert sind, siehe #Kräftefreier Kugelkreisel weiter unten.
| Herleitung der Winkelgeschwindigkeiten nach Euler[14] | ||||
| Die Winkelgeschwindigkeiten leiten sich aus den Konstanten
ab. Dazu wird für die Hauptträgheitsmomente Θ1 > Θ2 > Θ3 angenommen. Mit den beiden Konstanten können ω1 und ω3 als Funktionen von ω2 ausgedrückt werden:
mit Weil die Ausdrücke positiv sind, folgt Die zweite der Euler’schen Kreiselgleichungen liefert mit obigen ω1,2 Bei epizykloidischen Bewegungen ist und die Lösung ergibt sich mit ω2(t0) = 0, was abseits der zweiten Hauptachse immer irgendwann eintrifft, nach Trennung der Variablen und der Substitution q = x1sin(ϑ) zu Auf der rechten Seite steht ein Elliptisches Integral der 1. Art mit dem elliptischen Modul k = x1/x2, das eine Jacobische elliptische Funktion als Lösungsfunktion besitzt: Aus (*) können nun ω1 und ω3 unter Zuhilfenahme der Beziehungen zwischen den quadrierten jacobischen elliptischen Funktionen berechnet werden mit dem im Text angegebenen Resultat. Bei perizykloidischer Bewegung ist und das Ergebnis leitet sich mit vertauschten x1,2 ab. |
| Herleitung der Euler-Winkel |
| Vergleich der Komponenten des Drehimpulses in euler-Winkeln (siehe Kreiseltheorie#Bezugssysteme und Euler-Winkel) liefert im Hauptachsensystem ê1,2,3:
Der Winkel ψ bestimmt sich mit aus |
Bewegung auf der Separatrix[Bearbeiten | Quelltext bearbeiten]

Auf der Separatrix ist 2Θ2 Erot = L² und die Bewegung aperiodisch, weil die Winkelgeschwindigkeit keinen Zustand ein zweites Mal einnimmt. Die Bewegung des Kreisels ist hier dadurch gekennzeichnet, dass die von der 2-Achse und dem Drehimpuls aufgespannte Ebene mit konstanter Winkelgeschwindigkeit L/Θ2 um die Drehimpulsachse kreist und der Endpunkt der 2-Achse sich auf einer Loxodrome mit dem Richtungswinkel
der durch den Drehimpuls definierten Achse nähert, siehe Abb. 9.
Die Formeln des voran gegangenen Abschnitts sind hier zwar gültig, aber weil der elliptische Modul den Extremwert
annimmt, gehen die elliptischen Funktionen in die aperiodischen Hyperbelfunktionen über:
- und
Das Argument z und die Winkelgeschwindigkeiten des voran gegangenen Abschnitts spezialisieren sich damit zu:
Mit fortschreitender Zeit gehen ω1 und ω3 gegen null und ω2 gegen L/Θ2. Die Bewegung kommt einer Drehung um die 2-Achse beliebig nah ohne diesen Zustand jemals zu erreichen. In der Realität wird diese Bewegungsform kaum auftreten, denn bei der kleinsten Abweichung vom Idealfall 2Θ2 Erot = L² ist k ≠ 1 und die Winkelgeschwindigkeiten werden zu den periodischen des voran gegangenen Abschnitts. Die Bewegung auf der Separatrix ist instabil. Eine Bewegung nahe der Separatrix zeigt der Dschanibekow-Effekt.

Für die Berechnung der Bewegung wird, anders als im vorigen Abschnitt, der Ansatz für das lokale Basissystem benutzt, siehe Abb. 10 und vgl. Abb. 2.
Die eulerschen Winkel – siehe #Bewegungsfunktion des symmetrischen Kreisels – ergeben sich bei einem Drehimpuls in z-Richtung und einem Start mit ω2 = 0 zu
Die von der 2-Achse und dem Drehimpuls aufgespannte Ebene kreist mit konstanter Winkelgeschwindigkeit L/Θ2 um die Drehimpulsachse und der Winkel ϑ geht mit fortschreitender Zeit gegen null.
| Beweis |
| Im Basissystem
ergibt sich: Die Komponenten der Winkelgeschwindigkeit werden mit dem neuen Basissystem: Nun kann die Winkelgeschwindigkeit mit aus bestimmt werden zu Die Achse um die der Winkel ϑ dreht ist und der Meridian hat somit die Richtung Die Rate der 2-Achse ist Mit den obigen Zwischenergebnissen und den trigonometrischen Formeln berechnet sich der Richtungswinkel zwischen Meridian und der Rate des 2-Vektors zu der Konstanten Der Bruch in der Wurzel ist positiv und kleiner als eins: |
Kräftefreier Kugelkreisel[Bearbeiten | Quelltext bearbeiten]
Kugelkreisel haben drei gleiche Hauptträgheitsmomente, womit sich die #Kreiselgleichungen zu
vereinfachen. Beim kräftefreien Kugelkreisel sind Winkelgeschwindigkeit und Drehimpuls parallel, konstant und körperfest.
Einfluss der Reibung[Bearbeiten | Quelltext bearbeiten]
Der kräfefreie Kreisel ist eine Idealisierung, die unter den Bedingungen auf der Erde nur näherungsweise zu realisieren ist. Zum einen treten in den Lagern, die den Kreisel gegen die Gewichtskraft halten, unvermeidlich Reibmomente auf und ebenso führt die Haftbedingung der Luft an festen Oberflächen zu abbremsender Wechselwirkung mit der Umgebungsluft.[17]
Der Einfluss der Reibung in der kardanischen Aufhängung, wie in Abb. 1, macht sich beim symmetrischen Kreisel, je nachdem er gestreckt oder abgeplattet ist, unterschiedlich bemerkbar:
- Beim gestreckten Kreisel nimmt der Neigungswinkel ϑ gegenüber dem Drehimpuls zu und die Figurenachse wird zu einer labilen Drehachse.
- Beim abgeplatteten Kreisel nimmt der Neigungswinkel ϑ ab und die Figurenachse bleibt eine stabile Drehachse.
Beiden Kreiselformen ist gemeinsam, dass die Eigendrehgeschwindigkeit ω3 mit der Zeit abnimmt.
Die Luftreibung bremst ebenfalls die Eigendrehgeschwindigkeit und wirkt unterschiedlich auf gestreckte oder abgeplattete Kreisel:
- Beim gestreckten Kreisel richtet sich die Drehachse zunehmend senkrecht zur Figurenachse aus, die auch hier eine instabile Drehachse wird.
- Beim abgeplatteten Kreisel wandert die Drehgeschwindigkeit zur Figurenachse hin, die eine stabile Drehachse bleibt.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Trägheitsellipsoid informiert über Trägheits-, Energie- und Drallellipsoid
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Euler (1758), S. 173 und 190.
- ↑ Leimanis (1965), S. 53 ff.
- ↑ Magnus (1971), S. 100
- ↑ Arnold (1989), S. 154
- ↑ Arnold (1989), S. 142, Magnus (1971), S. 53, Leimanis (1965), S. 10.
- ↑ Arnold (1989), S. 151.
- ↑ Leimanis (1965), S. 11.
- ↑ Samuel Haughton: On the Rotation of a Solid Body Round a Fixed Point; Being an Account of the Late Professor Mac Cullagh's Lectures on That Subject. In: Royal Irish Academy (Hrsg.): The Transactions of the Royal Irish Academy. Vol. 22 (1849). Dublin university press, Dublin 1880, S. 139–154, JSTOR:30079824 (englisch, Haughtons Mitschrift einer Vorlesung von 1844. Siehe auch Magnus (1971), S. 61ff.).
- ↑ Magnus (1971), S. 82.
- ↑ a b Grammel (1920), S. 40, Grammel (1950), S. 53.
- ↑ Louis Poinsot: Théorie nouvelle de la rotation des corps. Bachelier, Paris 1834/1851.
- ↑ tennis racket theorem in der englischsprachigen Wikipedia.
- ↑ Mark S. Ashbaugh, Carmen C. Chicone, Richard H. Cushman: The twisting tennis racket. In: Journal of Dynamics and Differential Equations, 3, 1, 1991, S. 67–85.
- ↑ a b Magnus (1971), S. 64ff.
- ↑ Leimanis (1965), S. 17.
- ↑ Leimanis (1965), S. 18.
- ↑ Grammel (1920), S. 82 ff., Grammel (1950), S. 107 ff.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Leonhard Euler: Über die Bewegung der Rotation von starren Körpern um eine variable Achse. In: Königlich Preußische Akademie der Wissenschaften zu Berlin (Hrsg.): Mémoires de l’Académie des Sciences de Berlin. Band 14. Petersburg 1758, S. 173 und 190. (französisch, archive.org [abgerufen am 11. Januar 2020] Originaltitel: Du mouvement de rotation des corps solides autour d'un axe variable.).
- Herbert Goldstein, Charles P. Poole, Jr, John L. Safko: Klassische Mechanik. 3. Auflage. Wiley-VCH, Weinheim 2006, ISBN 3-527-40589-5.
- R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 573533210 (archive.org – "Schwung" bedeutet Drehimpuls, "Drehstoß" etwa Drehmoment und "Drehwucht" Rotationsenergie, siehe S. VII).
oder
R. Grammel: Der Kreisel. Theorie des Kreisels. 2. überarb. Auflage. Band 1. Springer, Berlin, Göttingen, Heidelberg 1950, DNB 451641299. - V. I. Arnold: Mathematical Methods of Classical Mechanics. 2. Auflage. Springer, New-York / Berlin / Heidelberg / London / Paris / Tokyo 1989, ISBN 3-540-96890-3.
- K. Magnus: Kreisel. Theorie und Anwendungen. Springer, Berlin / Heidelberg / New York 1971, ISBN 978-3-642-52163-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 5. Januar 2020]).
- Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 10 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 30. November 2019]).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Interaktive Animationen von Kreisel- und Pendelbewegungen (englisch).
- Freie Rotation eines quaderförmigen Körpers vom TIB AV-Portal der Technischen Informationsbibliothek.




















































































![{\displaystyle {\begin{aligned}{\vec {\omega }}=&[{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )]{\hat {e}}_{1}+[{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )]{\hat {e}}_{2}\\&+[{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}]{\hat {e}}_{3}\\=&[\underbrace {{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )} _{\omega _{3}}]{\hat {h}}_{3}+[\underbrace {{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )} _{\omega _{1}}]{\hat {h}}_{1}\\&+[\underbrace {{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}} _{\omega _{2}}]{\hat {h}}_{2}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/493f733ac182a1ec7489076cb4d5b2510554bdcf)






![{\displaystyle {\begin{aligned}\cos \eta =&{\frac {{\dot {\hat {h}}}_{2}\cdot {\hat {m}}}{|{\dot {\hat {h}}}_{2}||{\hat {m}}|}}={\frac {\omega _{1}\sin(\varphi )-\omega _{3}\cos(\varphi )}{\sqrt {\omega _{1}^{2}+\omega _{3}^{2}}}}={\frac {\left[\tan(\varphi )-{\frac {\omega _{3}}{\omega _{1}}}\right]\cos(\varphi )}{\sqrt {1+{\frac {\omega _{3}^{2}}{\omega _{1}^{2}}}}}}\\=&{\frac {\tan(\varphi )-{\frac {\Theta _{1}}{\Theta _{3}}}\tan(\varphi )}{{\sqrt {1+{\frac {\Theta _{1}^{2}}{\Theta _{3}^{2}}}\tan ^{2}(\varphi )}}{\sqrt {1+\tan ^{2}(\varphi )}}}}={\sqrt {\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{2}(\Theta _{1}+\Theta _{3}-\Theta _{2})}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3203b6af18926a46b6c4f2a217f2d902efd682)

