Varianz (Stochastik)

Die Varianz (lateinisch variantia „Verschiedenheit“ bzw. variare „(ver)ändern, verschieden sein“) ist ein Maß für die Streuung einer Wahrscheinlichkeitsdichte um ihren Schwerpunkt. Mathematisch wird sie definiert als die mittlere quadratische Abweichung einer reellen Zufallsvariablen von ihrem Erwartungswert. Sie ist das zentrale Moment zweiter Ordnung einer Zufallsvariablen.
Die Varianz kann mit einem Varianzschätzer, z. B. der Stichprobenvarianz, bestimmt werden. Die Quadratwurzel der Varianz ist das als Standardabweichung bezeichnete wichtigste Streuungsmaß in der Stochastik.
Die Bezeichnung Varianz wurde vor allem von dem britischen Statistiker Ronald Fisher (1890–1962) geprägt. Weitere Wörter für die Varianz sind das veraltete Dispersion (lateinisch dispersio „Zerstreuung“ bzw. dispergere „verteilen, ausbreiten, zerstreuen“), das Streuungsquadrat oder die Streuung.
Zu den Eigenschaften der Varianz gehört, dass sie niemals negativ ist und sich bei Verschiebung der Verteilung nicht ändert. Die Varianz einer Summe unkorrelierter Zufallsvariablen ist gleich der Summe ihrer Varianzen. Ein Nachteil der Varianz für praktische Anwendungen ist, dass sie im Unterschied zur Standardabweichung eine andere Einheit als die Zufallsvariable besitzt. Da sie über ein Integral definiert wird, existiert sie nicht für alle Verteilungen, d. h., sie kann auch unendlich sein.
Eine Verallgemeinerung der Varianz ist die Kovarianz. Im Unterschied zur Varianz, die die Variabilität der betrachteten Zufallsvariablen misst, ist die Kovarianz ein Maß für die gemeinsame Variabilität von zwei Zufallsvariablen. Aus dieser Definition der Kovarianz folgt, dass die Kovarianz einer Zufallsvariablen mit sich selbst gleich der Varianz dieser Zufallsvariablen ist. Im Falle eines reellen Zufallsvektors kann die Varianz zur Varianz-Kovarianzmatrix verallgemeinert werden.
Definition[Bearbeiten | Quelltext bearbeiten]
Die Varianz wird zuerst mathematisch definiert, eine Erklärung der Definition folgt danach. Die Varianz einer Stichprobe ist ein Spezialfall der mathematischen Definition und wird im Abschnitt Empirische Varianz / Stichprobenvarianz behandelt.
Mathematische Definition[Bearbeiten | Quelltext bearbeiten]
Sei ein Wahrscheinlichkeitsraum und eine Zufallsvariable auf diesem Raum. Die Varianz ist definiert als die zu erwartende quadratische Abweichung dieser Zufallsvariablen von ihrem Erwartungswert , sofern dieser existiert:[1]
Erklärung der Definition[Bearbeiten | Quelltext bearbeiten]
Die Definition sagt Folgendes: Gegeben ist eine Zufallsvariable mit Erwartungswert .
Der Wahrscheinlichkeitsraum[Bearbeiten | Quelltext bearbeiten]
Zu einer Zufallsvariable gehört immer auch ein Wahrscheinlichkeitsraum, denn eine Zufallsvariable ist aus mathematischer Sicht eine Funktion von diesem Raum. Für ein oberflächliches Verständnis des Begriffes der Varianz kann der Begriff aber auch übersprungen werden.
Die erste Gleichung[Bearbeiten | Quelltext bearbeiten]
Die erste Gleichung
sagt, dass die Varianz von dasselbe wie der Erwartungswert der Zufallsvariable ist. Diese neue Zufallsvariable ist die quadratische Abweichung von zu und man spricht von der mittleren quadratischen Abweichung, weil man den Erwartungswert der quadratischen Abweichung nimmt.
Nach den Rechenregeln des Erwartungswertes lässt sich die rechte Seite leicht umformen
- .
Die zweite Gleichung[Bearbeiten | Quelltext bearbeiten]
Die zweite Gleichung
sagt, dass sich der Erwartungswert von direkt als Integral berechnen lässt. Dieses Integral ist hier in der allgemeinen Form, wo man über den Ergebnisraum integriert, um alle Fälle miteinzuschließen. Hier gibt es noch die wichtigen Fälle:
- Absolutstetiger Fall: Hat man eine Zufallsvariable mit einer Dichte von einer Menge , so ist dieses Integral gleichwertig zu
- Diskreter Fall: Hat man eine Zufallsvariable mit einer Wahrscheinlichkeitsfunktion von einer Menge , so ist dieses Integral gleichwertig zu
Diese Gleichungen zeigen, dass die Varianz eine Kennzahl der Wahrscheinlichkeitsverteilung von ist.
Empirische Varianz / Stichprobenvarianz[Bearbeiten | Quelltext bearbeiten]
Ein Spezialfall der Varianz einer diskreten Zufallsvariable ist die (unkorrigierte) empirische Varianz. Sie ist die Varianz einer Stichprobe von Werten und die Varianz der empirischen Verteilung. Man erhält den Spezialfall, wenn man die Wahrscheinlichkeitsfunktion und als Erwartungswert den empirischen Mittelwert
wählt. Die unkorrigierte empirische Varianz ist dann
Die Bessel-Korrektur
liefert die korrigierte empirische Varianz
Beispiel:
Sei , dann ist und der empirische Mittelwert , was folgende unkorrigierte empirische Varianz und folgende korrigierte empirische Varianz gibt.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
- Sofern die Varianz existiert, gilt . Die Varianz kann aber auch den Wert annehmen, wie es bei der Lévy-Verteilung der Fall ist. Eine Verteilung, die keine Varianz hat, ist die Cauchy-Verteilung, da für diese schon der Erwartungswert nicht existiert.
- Falls man die zentrierte Zufallsvariable betrachtet, so ist die Varianz deren zweites Moment .
- Falls eine Zufallsvariable quadratisch integrierbar ist, das heißt , so sind wegen des Verschiebungssatzes ihre Varianz und ihr Erwartungswert endliche Größen:
Interpretation als Funktional[Bearbeiten | Quelltext bearbeiten]
Die Varianz ist ein Funktional auf dem Raum der Zufallsvariablen mit endlichem Erwartungswert. Sie kann aber auch als nichtlineares Funktional auf dem Raum aller Wahrscheinlichkeitsverteilungen , die einen endlichen Erwartungswert besitzen, verstanden werden:
Dabei werden die Wahrscheinlichkeitsverteilungen mit ihren Verteilungsfunktionen identifiziert. Für Wahrscheinlichkeitsverteilungen, deren Erwartungswert nicht endlich ist, ist die Varianz nicht definiert.
Notation[Bearbeiten | Quelltext bearbeiten]
Da die Varianz ein Funktional ist, wird sie wie der Erwartungswert (besonders in anglophoner Literatur) oft auch mit eckigen Klammern geschrieben. Sie wird mitunter als [A 1] oder notiert. Besteht keine Verwechslungsgefahr, wird sie einfach als (lies: Sigma Quadrat) notiert. Da die Varianz vor allem in älterer Literatur auch als Dispersion beziehungsweise Streuung bezeichnet wurde,[2][3] begegnet man häufig der Notation .[4]
Die Notation mit dem Quadrat des griechischen Buchstabens Sigma rührt daher, dass die Berechnung der Varianz der Dichtefunktion einer Normalverteilung genau dem Parameter der Normalverteilung entspricht. Da die Normalverteilung in der Stochastik eine sehr wichtige Rolle spielt, wird die Varianz im Allgemeinen mit notiert (siehe auch Abschnitt Varianzen spezieller Verteilungen). Des Weiteren wird in der Statistik und insbesondere in der Regressionsanalyse das Symbol verwendet, um die wahre unbekannte Varianz der Störgrößen zu kennzeichnen.
Einführung in die Problemstellung[Bearbeiten | Quelltext bearbeiten]
Als Ausgangspunkt für die Konstruktion der Varianz betrachtet man eine beliebige Größe, die vom Zufall abhängig ist und somit unterschiedliche Werte annehmen kann. Diese Größe, die im Folgenden mit bezeichnet wird, folgt einer bestimmten Verteilung. Der Erwartungswert dieser Größe wird mit
abgekürzt[A 2] und gibt an, welchen Wert die Zufallsvariable im Mittel annimmt. Er kann als Schwerpunkt der Verteilung interpretiert werden (siehe auch Abschnitt Interpretation) und gibt ihre Lage wieder. Zur hinreichenden Charakterisierung einer Verteilung bedarf es jedoch noch einer Größe, die als Kennzahl Auskunft über die Stärke der Streuung einer Verteilung um ihren Schwerpunkt gibt.[5] Diese Größe sollte stets größer oder gleich Null sein, da sich negative Streuung nicht sinnvoll interpretieren lässt. Ein erster naheliegender Ansatz wäre, die mittlere absolute Abweichung der Zufallsvariablen von ihrem Erwartungswert heranzuziehen:[6]
Da die in der Definition der mittleren absoluten Abweichung verwendete Betragsfunktion nicht überall differenzierbar ist und ansonsten in der Statistik für gewöhnlich Quadratsummen benutzt werden,[7][8] ist es sinnvoll, statt mit der mittleren absoluten Abweichung mit der mittleren quadratischen Abweichung, also der Varianz, zu operieren.[A 3]
Berechnung der Varianz[Bearbeiten | Quelltext bearbeiten]
Varianz bei diskreten Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Eine Zufallsvariable mit einem endlichen oder abzählbar unendlichen Wertebereich [A 4] wird diskret genannt. Ihre Varianz berechnet sich dann als gewichtete Summe der Abweichungsquadrate (vom Erwartungswert):[9]
Hierbei ist die Wahrscheinlichkeit, dass den Wert annimmt. Es wird in obiger Summe also jede mögliche Ausprägung mit der Wahrscheinlichkeit ihres Auftretens gewichtet.[10] Die Varianz ist bei diskreten Zufallsvariablen also eine gewichtete Summe mit den Gewichten . Der Erwartungswert einer diskreten Zufallsvariablen stellt ebenfalls eine gewichtete Summe dar, die durch
gegeben ist. Die Summen erstrecken sich jeweils über alle Werte, die diese Zufallsvariable annehmen kann. Im Falle eines abzählbar unendlichen Wertebereichs ergibt sich eine unendliche Summe. In Worten berechnet sich die Varianz, im diskreten Fall, als Summe der Produkte der Wahrscheinlichkeiten der Realisierungen der Zufallsvariablen mit der jeweiligen quadrierten Abweichung.
Varianz bei stetigen Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Eine Zufallsvariable wird als stetig bezeichnet, wenn ihr Wertebereich eine überabzählbare Menge ist. Falls die Zufallsvariable absolut stetig ist, dann existiert als Konsequenz des Satzes von Radon-Nikodým eine Wahrscheinlichkeitsdichtefunktion (kurz: Dichte) . Im Fall einer reellwertigen Zufallsvariablen lässt sich die Verteilungsfunktion , , wie folgt als Integral darstellen:
Für die Varianz einer reellwertigen Zufallsvariablen mit Dichte gilt nun
- ,
wobei ihr Erwartungswert gegeben ist durch .[11]
Die Varianz berechnet sich bei Existenz einer Dichte als das Integral über das Produkt der quadrierten Abweichung und der Dichtefunktion der Verteilung. Es wird also über den Raum aller möglichen Ausprägungen (möglicher Wert eines statistischen Merkmals) integriert.
Geschichte[Bearbeiten | Quelltext bearbeiten]


Das Konzept der Varianz geht auf Carl Friedrich Gauß zurück. Gauß führte den mittleren quadratischen Fehler ein, um zu zeigen, wie sehr ein Punktschätzer um den zu schätzenden Wert streut. Diese Idee wurde von Karl Pearson, dem Begründer der Biometrie, übernommen. Er ersetzte, für dieselbe Idee, den von Gauß geprägten Begriff mittlerer Fehler durch seinen Begriff Standardabweichung. Diesen verwendet er im Anschluss in seinen Vorlesungen. Der Gebrauch des griechischen Buchstabens Sigma für die Standardabweichung wurde von Pearson erstmals 1894 in seiner Serie von achtzehn Arbeiten mit dem Titel Mathematische Beiträge zur Evolutionstheorie (Originaltitel: Contributions to the Mathematical Theory of Evolution) eingeführt. Er schrieb dort: „[…] dann wird seine Standardabweichung (Fehler des mittleren Quadrats)“. Im Jahre 1901 gründete Pearson dann die Zeitschrift Biometrika, die eine wichtige Grundlage der angelsächsischen Schule der Statistik wurde.
Die Bezeichnung „Varianz“ wurde vom Statistiker Ronald Fisher in seinem 1918 veröffentlichtem Aufsatz mit dem Titel Die Korrelation zwischen Verwandten in der Annahme der Mendelschen Vererbung (Originaltitel: The Correlation between Relatives on the Supposition of Mendelian Inheritance) eingeführt. Ronald Fisher schreibt:
„Der große Körper der verfügbaren Statistiken zeigt uns, dass die Abweichungen einer menschlichen Messung von ihrem Mittel sehr genau dem Gesetz der Normalverteilung der Störgrößen folgen, und, folglich, dass die Variabilität gleichmäßig durch die Standardabweichung gemessen werden kann, die der Quadratwurzel des mittleren quadratischen Fehlers entspricht. Wenn es zwei unabhängige Ursachen der Variabilität gibt, die in der Lage sind, in einer ansonsten gleichmäßigen Populationsverteilung die Standardabweichungen and zu produzieren, wird festgestellt, dass die Verteilung, wenn beide Ursachen zusammen interagieren, eine Standardabweichung von aufweist. Es ist daher wünschenswert, die Ursachen der Variabilität zu analysieren, um mit dem Quadrat der Standardabweichung als einem Maß für die Variabilität umzugehen. Wir sollten diese Größe die Varianz taufen […]“
Fisher führte kein neues Symbol ein, sondern benutzte lediglich zur Notation der Varianz. In den folgenden Jahren entwickelte er ein genetisches Modell, das zeigt, dass eine kontinuierliche Variation zwischen phänotypischen Merkmalen, die von Biostatistikern gemessen wurde, durch die kombinierte Wirkung vieler diskreter Gene erzeugt werden kann und somit das Ergebnis einer mendelschen Vererbung ist. Auf diesen Resultaten aufbauend formulierte Fisher dann sein fundamentales Theorem der natürlichen Selektion, das die Gesetzmäßigkeiten der Populationsgenetik für die Zunahme der Fitness von Organismen beschreibt. Zusammen mit Pearson entwickelte er u. a. die Grundlagen der Versuchsplanung (1935 erschien The Design of Experiments) und der Varianzanalyse. Des Weiteren lässt sich die Mehrzahl der biometrischen Methoden auf Pearson und Fisher zurückführen, auf deren Grundlage Jerzy Neyman und Egon Pearson in den 1930er Jahren die allgemeine Testtheorie entwickelten.[13]
Kenngröße einer Wahrscheinlichkeitsverteilung[Bearbeiten | Quelltext bearbeiten]
Jede Wahrscheinlichkeitsverteilung oder Zufallsvariable kann durch sogenannte Kenngrößen (auch Parameter genannt) beschrieben werden, die diese Verteilung charakterisieren. Die Varianz und der Erwartungswert sind die wichtigsten Kenngrößen einer Wahrscheinlichkeitsverteilung. Sie werden bei einer Zufallsvariablen als Zusatzinformationen wie folgt angegeben: . In Worten: Die Zufallsvariable folgt einer (hier nicht näher spezifizierten) Verteilung mit Erwartungswert und Varianz . Für den Fall, dass die Zufallsvariable einer speziellen Verteilung folgt, zum Beispiel einer Standardnormalverteilung, wird dies wie folgt notiert: . Der Erwartungswert von ist also Null und die Varianz Eins. Weitere wichtige Kenngrößen einer Wahrscheinlichkeitsverteilung stellen neben den Momenten beispielsweise der Median, der Modus oder Quantile dar.[14] Die Kenngrößen einer Wahrscheinlichkeitsverteilung entsprechen in der deskriptiven Statistik den Kenngrößen einer Häufigkeitsverteilung.
Sätze über die Varianz[Bearbeiten | Quelltext bearbeiten]
Tschebyscheffsche Ungleichung[Bearbeiten | Quelltext bearbeiten]
Mithilfe der Tschebyscheffschen Ungleichung lässt sich unter Verwendung der existierenden ersten beiden Momente die Wahrscheinlichkeit dafür abschätzen, dass die Zufallsvariable Werte in bestimmten Intervallen der reellen Zahlengeraden annimmt, ohne jedoch die Verteilung von zu kennen. Sie lautet für eine Zufallsvariable mit Erwartungswert und Varianz :[15]
Die Tschebyscheffsche Ungleichung gilt sowohl für symmetrische als auch für schiefe Verteilungen, sie setzt also keine besondere Verteilungsform voraus. Ein Nachteil der Tschebyscheffschen Ungleichung ist, dass sie nur eine grobe Abschätzung liefert.
Popovicius Ungleichung für Varianzen[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der Ungleichung von Popoviciu kann man die Varianz nach oben beschränken. Sei eine Zufallsvariable mit Varianz und , , dann gilt:
Gesetz der totalen Varianz[Bearbeiten | Quelltext bearbeiten]
Das Gesetz der totalen Varianz (auch Gesetz der iterierten Varianz oder Eves Gesetz) sagt: Falls zwei Zufallsvariablen auf dem gleichen Wahrscheinlichkeitsraum sind und die Varianz von endlich ist, dann gilt:
Allgemeiner gilt: Wenn und , dann gilt
Interpretation[Bearbeiten | Quelltext bearbeiten]
Physikalische Interpretation[Bearbeiten | Quelltext bearbeiten]
Die Varianz ist neben dem Erwartungswert die zweite wichtige Kenngröße der Verteilung einer reellen Zufallsvariablen. Das -te zentrale Moment von ist . Für wird das zentrale Moment zweiter Ordnung Varianz der Verteilung von genannt.[16] Der Begriff „Moment“ stammt originär aus der Physik. Wenn man die möglichen Werte als Massepunkte mit den Massen auf der (als gewichtslos angenommenen) reellen Zahlengeraden interpretiert, dann erhält man eine physikalische Interpretation des Erwartungswertes: Das erste Moment, der Erwartungswert, stellt dann den physikalischen Schwerpunkt beziehungsweise Massenmittelpunkt des so entstehenden Körpers dar.[17] Die Varianz kann dann als Trägheitsmoment des Massesystems bezüglich der Rotationsachse um den Schwerpunkt interpretiert werden.[18] Im Gegensatz zum Erwartungswert, der also die Wahrscheinlichkeitsmasse balanciert, ist die Varianz ein Maß für die Streuung der Wahrscheinlichkeitsmasse um ihren Erwartungswert.
Interpretation als Abstand[Bearbeiten | Quelltext bearbeiten]
Die Interpretation der Varianz einer Zufallsvariablen als mittlerer quadrierter Abstand lässt sich wie folgt erklären: Der Abstand zwischen zwei Punkten und auf der reellen Zahlengeraden ist gegeben durch . Wenn man jetzt definiert, dass ein Punkt die Zufallsvariable ist und der andere , dann gilt , und der quadrierte Abstand lautet . Folglich wird als der mittlere quadrierte Abstand zwischen der Realisierung der Zufallsvariablen und dem Erwartungswert interpretiert, wenn das Zufallsexperiment unendlich oft wiederholt wird.[19]
Interpretation als Maß für Determinismus[Bearbeiten | Quelltext bearbeiten]
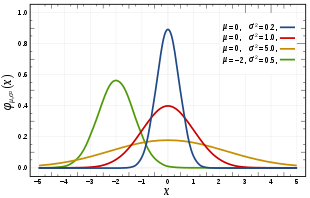
Die Varianz beschreibt außerdem die Breite einer Wahrscheinlichkeitsfunktion[20] und daher, wie „stochastisch“ oder wie „deterministisch“ ein betrachtetes Phänomen ist. Bei einer großen Varianz liegt eher eine stochastische Situation vor und bei einer kleinen Varianz eher eine deterministische.[21] Im Spezialfall einer Varianz von Null liegt eine vollständig deterministische Situation vor. Die Varianz ist genau dann Null, wenn die Zufallsvariable mit hundertprozentiger Wahrscheinlichkeit nur einen bestimmen Wert, nämlich den Erwartungswert, annimmt – wenn also gilt. So eine „Zufallsvariable“ ist mit Wahrscheinlichkeit eins konstant und kann in diesem Sinn als „deterministisch“ bezeichnet werden.[22] Da für eine Zufallsvariable mit dieser Eigenschaft für alle gilt, wird deren Verteilung manchmal auch als „entartet“ bezeichnet.[22] Eine Wahrscheinlichkeitsverteilung mit für eine reelle Zahl heißt degenerierte Wahrscheinlichkeitsverteilung oder Dirac-Verteilung.
Der Unterschied zwischen einer Konstanten , die einer reellen Zufallsvariablen mit der Eigenschaft für alle entspricht, und einer Zufallsvariablen mit der Eigenschaft ist, dass im zweiten Fall realisierte Werte der Zufallsvariablen möglich sind, die von verschieden sind, die aber insgesamt die Wahrscheinlichkeit null haben, es gilt also . In beiden Fällen hat die Varianz den Wert Null.
Im Gegensatz zu diskreten Zufallsvariablen gilt für stetige Zufallsvariablen stets für jedes .[23] Im stetigen Fall beschreibt die Varianz die Breite einer Dichtefunktion. Die Breite wiederum ist ein Maß für die Unsicherheit, die mit einer Zufallsvariable verbunden ist. Je schmaler die Dichtefunktion ist, desto genauer kann der Wert von vorhergesagt werden.
Rechenregeln und Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Die Varianz weist eine Fülle nützlicher Eigenschaften auf, welche die Varianz zum wichtigsten Streuungsmaß macht:[24]
Verschiebungssatz[Bearbeiten | Quelltext bearbeiten]
Der Verschiebungssatz ist das stochastische Analogon zum Steinerschen Satz zur Berechnung von Trägheitsmomenten. Es gilt mit und für beliebiges reelles
- ,
d. h., die mittlere quadratische Abweichung von bzgl. (physikalisch: das Trägheitsmoment bzgl. der Achse ) ist gleich der Varianz (physikalisch: gleich dem Trägheitsmoment bzgl. der Achse durch den Schwerpunkt ) plus dem Quadrat der Verschiebung .
Der mittlere Term ergibt unter Ausnutzung der Linearität des Erwartungswertes:[25]
Aus dem Verschiebungssatz ergibt sich überdies für beliebiges reelles :
- bzw.
Siehe auch Fréchet-Prinzip.
Für erhält man als bekannteste Variante des Verschiebungssatzes:
Die Varianz als zentrales, auf den Erwartungswert (das „Zentrum“) bezogenes Moment lässt sich also auch als nichtzentrales Moment ausdrücken.
Aus dem Verschiebungssatz folgt wegen der Nichtnegativitätsbedingung der Varianz , somit gilt . Dieses Resultat ist ein Spezialfall der jensenschen Ungleichung für Erwartungswerte. Der Verschiebungssatz beschleunigt die Berechnung der Varianz, da der dazu nötige Erwartungswert von zusammen mit gebildet werden kann, während sonst bereits bekannt sein muss – konkret für diskrete beziehungsweise stetige Zufallsvariablen liefert er:
| Falls diskret | Falls stetig |
Lineare Transformation[Bearbeiten | Quelltext bearbeiten]
Für zwei Konstanten gilt:
- Die Varianz einer Konstanten ist Null, da Konstanten per Definition nicht zufällig sind und somit auch nicht streuen: ;
- Translationsinvarianz: Für additive Konstanten gilt . Dies bedeutet, dass eine „Verschiebung der Zufallsvariablen“ um einen konstanten Betrag keine Auswirkung auf deren Streuung hat.
- Im Gegensatz zu additiven Konstanten haben multiplikative Konstanten eine Auswirkung auf die Skalierung der Varianz. Bei multiplikativen Konstanten wird die Varianz mit der quadrierten der Konstanten, also , skaliert.[26] Dies kann wie folgt gezeigt werden:
Hierbei wurde die Eigenschaft der Linearität des Erwartungswertes benutzt. Zusammengefasst ergibt die Varianzbildung einer linearen transformierten Zufallsvariablen :
Insbesondere für folgt , das heißt, das Vorzeichen der Varianz ändert sich nicht, wenn sich das Vorzeichen der Zufallsvariablen ändert.
Jede Zufallsvariable kann durch Zentrierung und anschließende Normierung, genannt Standardisierung, in eine Zufallsvariable überführt werden. Diese Normierung ist eine lineare Transformation. Die derart standardisierte Zufallsvariable weist eine Varianz von und einen Erwartungswert von auf.
Beziehung zur Standardabweichung[Bearbeiten | Quelltext bearbeiten]
Die Varianz einer Zufallsvariablen wird immer in Quadrateinheiten angegeben.[27] Dies ist problematisch, weil quadrierte Einheiten, die auf diesem Wege zustande kommen – wie zum Beispiel –, keine sinnvolle Interpretation bieten; die Interpretation als Flächenmaß ist im vorliegenden Beispiel unzulässig. Um die gleiche Einheit wie die Zufallsvariable zu erhalten, wird daher statt der Varianz i. d. R. die Standardabweichung verwendet. Sie hat die gleiche Einheit wie die Zufallsvariable selbst und misst somit, bildlich gesprochen, „mit dem gleichen Maß“.
Die Standardabweichung ist die Quadratwurzel aus der Varianz:[28][29]
Sie wird als (gelegentlich auch als ), , oder einfach als (Sigma) notiert. Ferner eignet sich die Standardabweichung zur Quantifizierung von Unsicherheit bei Entscheidungen unter Risiko, weil sie, im Unterschied zur Varianz, den Anforderungen an ein Risikomaß genügt.
Bei einigen Wahrscheinlichkeitsverteilungen, insbesondere der Normalverteilung, können aus der Standardabweichung direkt Wahrscheinlichkeiten berechnet werden. So befinden sich bei der Normalverteilung immer ca. 68 % der Werte im Intervall von der Breite von zwei Standardabweichungen um den Erwartungswert. Beispiel hierfür ist die Körpergröße: Sie ist für eine Nation und Geschlecht annähernd normalverteilt, sodass z. B. in Deutschland 2006 ca. 68 % aller Männer etwa zwischen 171 und 186 cm groß waren (ca. , also „Erwartungswert plus/minus Standardabweichung“).[30]
Für die Standardabweichung gilt für jede Konstante : . Im Gegensatz zur Varianz gilt für die Standardabweichung die Rechenregel mit für lineare Transformationen, das heißt, die Standardabweichung wird im Gegensatz zur Varianz nicht mit dem Quadrat der Konstanten skaliert. Insbesondere gilt für : .
Beziehung zur Kovarianz[Bearbeiten | Quelltext bearbeiten]
Im Gegensatz zur Varianz, die lediglich die Variabilität der betrachteten Zufallsvariablen misst, misst die Kovarianz die gemeinsame Variabilität von zwei Zufallsvariablen. Die Varianz ist demnach die Kovarianz einer Zufallsvariablen mit sich selbst: . Diese Beziehung folgt direkt aus den Definition von Varianz und Kovarianz. Die Kovarianz zwischen und wird auch mit abgekürzt. Außerdem gilt, da die Kovarianz eine positiv semidefinite Bilinearform ist, die Cauchy-Schwarzsche Ungleichung:
Diese bedeutende Ungleichung findet vor allem in der linearen Algebra Anwendung.
Summen[Bearbeiten | Quelltext bearbeiten]
Für die Varianz einer beliebigen Summe von Zufallsvariablen gilt allgemein:[31][32]
Hierbei bezeichnet die Kovarianz der Zufallsvariablen und und es wurde die Eigenschaft verwendet. Berücksichtigt man das Verhalten der Varianz bei linearen Transformationen, dann gilt für die Varianz einer Linearkombination (einer gewichteten Summe) zweier Zufallsvariablen:
Speziell für zwei Zufallsvariablen , und ergibt sich:[33]
Dies bedeutet, dass die Variabilität der Summe zweier Zufallsvariablen gleich der Summe der einzelnen Variabilitäten und dem Zweifachen der gemeinsamen Variabilität der beiden Zufallsvariablen ist.
Ein weiterer Grund, warum die Varianz anderen Streuungsmaßen vorgezogen wird, ist die nützliche Eigenschaft, dass die Varianz der Summe unabhängiger Zufallsvariablen gleich der Summe der Varianzen ist:[26][34]
Dies resultiert daraus, dass bei unabhängigen Zufallsvariablen gilt. Diese Formel lässt sich auch verallgemeinern: Wenn paarweise unkorrelierte Zufallsvariablen sind (das heißt, ihre Kovarianzen sind alle gleich Null), gilt
oder allgemeiner mit beliebigen Konstanten :
Dieses Resultat wurde 1853 vom französischen Mathematiker Irénée-Jules Bienaymé entdeckt und wird daher auch als Gleichung von Bienaymé bezeichnet.[35][36] Sie gilt insbesondere dann, wenn die Zufallsvariablen unabhängig sind, denn aus Unabhängigkeit folgt Unkorreliertheit. Wenn alle Zufallsvariablen die gleiche Varianz haben, bedeutet dies für die Varianzbildung des Stichprobenmittels:
Man kann erkennen, dass die Varianz des Stichprobenmittels sinkt, wenn der Stichprobenumfang steigt. Diese Formel für die Varianz des Stichprobenmittels wird bei der Definition des Standardfehlers des Stichprobenmittels benutzt, der im zentralen Grenzwertsatz angewendet wird.
Produkte[Bearbeiten | Quelltext bearbeiten]
Sind zwei Zufallsvariablen und unabhängig, dann ist die Varianz ihres Produktes gegeben durch:[37]
Zusammengesetzte Zufallsvariable[Bearbeiten | Quelltext bearbeiten]
Ist eine zusammengesetzte Zufallsvariable, d. h., sind unabhängige Zufallsvariablen, sind die identisch verteilt und ist auf definiert, so lässt sich darstellen als . Existieren die zweiten Momente von , so gilt für die zusammengesetzte Zufallsvariable:
Diese Aussage ist auch als Blackwell-Girshick-Gleichung bekannt und wird z. B. in der Schadensversicherungsmathematik benutzt.
Momenterzeugende und kumulantenerzeugende Funktion[Bearbeiten | Quelltext bearbeiten]
Mithilfe der momenterzeugenden Funktion lassen sich Momente wie die Varianz häufig einfacher berechnen. Die momenterzeugende Funktion ist definiert als Erwartungswert der Funktion . Da für die momenterzeugende Funktion der Zusammenhang[38]
gilt, lässt sich die Varianz, durch den Verschiebungssatz, damit auf folgende Weise berechnen:
Hierbei ist die momenterzeugende Funktion und deren -te Ableitung. Die kumulantenerzeugende Funktion einer Zufallsvariablen ergibt sich als Logarithmus der momenterzeugenden Funktion und ist definiert als:
Leitet man sie zweimal ab und wertet sie an der Stelle null aus, so erhält man für die Varianz . Die zweite Kumulante ist also die Varianz.
Charakteristische und wahrscheinlichkeitserzeugende Funktion[Bearbeiten | Quelltext bearbeiten]
Die Varianz einer Zufallsvariablen lässt sich auch mit Hilfe ihrer charakteristischen Funktion darstellen. Wegen
folgt nämlich mit dem Verschiebungssatz:[39]
Auch mit der wahrscheinlichkeitserzeugenden Funktion , die in Beziehung zur charakteristische Funktion steht, lässt sich für diskrete die Varianz berechnen. Es gilt dann für die Varianz , falls der linksseitige Grenzwert existiert.
Varianz als mittlere quadratische Abweichung vom Mittelwert[Bearbeiten | Quelltext bearbeiten]
Im Falle einer diskreten Zufallsvariablen mit abzählbar endlichem Träger ergibt sich für die Varianz der Zufallsvariablen :
Hierbei ist die Wahrscheinlichkeit, dass den Wert annimmt. Diese Varianz kann als Summe der Werte , gewichtet mit den Wahrscheinlichkeiten , interpretiert werden.
Falls gleichverteilt auf ist (), ist der Erwartungswert gleich dem arithmetischen Mittel (siehe Gewichtetes arithmetisches Mittel als Erwartungswert):
Folglich wird die Varianz zum arithmetischen Mittel der Werte :
D. h., die Varianz ist bei Gleichverteilung gerade die mittlere quadratische Abweichung vom Mittelwert bzw. die Stichprobenvarianz .
Varianzen spezieller Verteilungen[Bearbeiten | Quelltext bearbeiten]
In der Stochastik gibt es eine Vielzahl von Verteilungen, die meist eine unterschiedliche Varianz aufweisen und oft in Beziehung zueinander stehen. Die Varianz der Normalverteilung ist von großer Bedeutung, da die Normalverteilung in der Statistik eine außerordentliche Stellung einnimmt. Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind. Eine Auswahl wichtiger Varianzen ist in nachfolgender Tabelle zusammengefasst:
| Verteilung | Stetig/diskret | Wahrscheinlichkeitsfunktion | Varianz |
| Normalverteilung | Stetig | ||
| Cauchy-Verteilung | Stetig | existiert nicht | |
| Bernoulli-Verteilung | Diskret | ||
| Binomialverteilung | Diskret | ||
| Stetige Gleichverteilung | Stetig | ||
| Poisson-Verteilung | Diskret | ||
| Degenerierte Verteilung | Diskret |
Beispiele[Bearbeiten | Quelltext bearbeiten]
Berechnung bei diskreten Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Münzwurf[Bearbeiten | Quelltext bearbeiten]
Eine Münze wird 7-mal geworfen. Wenn die diskrete Zufallsvariable die Anzahl der Würfe zählt, mit denen „Zahl“ geworfen wird, ergibt sich für die Binomialverteilung
mit und . Die Werte und ihre Wahrscheinlichkeiten lassen sich in folgender Tabelle zusammenfassen:
Der Erwartungswert beträgt
und daher ist die Varianz gegeben durch:
Auch mit dem Verschiebungssatz erhält man diesen Wert für die Varianz:
Für die Standardabweichung ergibt sich damit:
Community Cards bei Texas Hold’em[Bearbeiten | Quelltext bearbeiten]
Bei der Pokervariante Texas Hold’em werden von den 52 Spielkarten 5 Community Cards aufgedeckt. Wenn die diskrete Zufallsvariable die Anzahl der Asse zählt, die aufgedeckt werden, ergibt sich für die hypergeometrische Verteilung mit Spielkarten, Assen und Community Cards. Die Werte und ihre Wahrscheinlichkeiten lassen sich in folgender Tabelle zusammenfassen:
Der Erwartungswert beträgt
und daher ist die Varianz gegeben durch:
Für die Standardabweichung ergibt sich damit:
Berechnung bei stetigen Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
Eine stetige Zufallsvariable habe die Dichtefunktion
mit den Erwartungswerten:
Die Varianz dieser Dichtefunktion berechnet sich mit Hilfe des Verschiebungssatzes wie folgt:
Stichprobenvarianz als Schätzer für die Varianz[Bearbeiten | Quelltext bearbeiten]
Seien reelle unabhängig und identisch verteilte Zufallsvariablen mit dem Erwartungswert und der endlichen Varianz . Ein Schätzer für den Erwartungswert stellt das Stichprobenmittel dar, da nach dem Gesetz der großen Zahlen gilt:
Es wird im Folgenden ein Schätzer für die Varianz gesucht. Ausgehend von definiert man sich die Zufallsvariablen . Diese sind unabhängig und identisch verteilt mit dem Erwartungswert . Ist nun quadratisch integrierbar, dann ist das schwache Gesetz der großen Zahlen anwendbar und es gilt:
Wenn man nun durch ersetzt, liefert dies die sogenannte Stichprobenvarianz. Aus diesem Grund stellt wie oben gezeigt die Stichprobenvarianz
eine induktive Entsprechung der Varianz im stochastischen Sinne dar.[40]
Bedingte Varianz[Bearbeiten | Quelltext bearbeiten]
Analog zu bedingten Erwartungswerten lassen sich beim Vorliegen von Zusatzinformationen, wie beispielsweise den Werten einer weiteren Zufallsvariablen, bedingte Varianzen bedingter Verteilungen betrachten. Es seien und zwei reelle Zufallsvariablen, dann heißt die Varianz von , die auf konditioniert ist,[41]
die bedingte Varianz von gegeben (oder Varianz von bedingt auf ).[42] Um die „gewöhnliche“ Varianz stärker von der bedingten Varianz zu unterscheiden, spricht man bei der gewöhnlichen Varianz auch von der unbedingten Varianz.
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Varianz-Kovarianzmatrix[Bearbeiten | Quelltext bearbeiten]
Im Falle eines reellen Zufallsvektors mit dem dazugehörigen Erwartungswertvektor[43] verallgemeinern sich die Varianz und die Kovarianz zur symmetrischen Varianz-Kovarianzmatrix (oder einfach Kovarianzmatrix) des Zufallsvektors:[44]
Der Eintrag der -ten Zeile und -ten Spalte der Varianz-Kovarianzmatrix ist die Kovarianz der Zufallsvariablen und und in der Diagonale stehen die Varianzen .[45] Da die Kovarianzen ein Maß für die Korrelation zwischen Zufallsvariablen darstellen und die Varianzen lediglich ein Maß für die Variabilität, enthält die Varianz-Kovarianzmatrix Informationen über die Streuung und Korrelationen zwischen all ihren Komponenten. Da die Varianzen und Kovarianzen per definitionem stets nichtnegativ sind, gilt analog für die Varianz-Kovarianzmatrix, dass sie positiv semidefinit ist.[46] Die Varianz-Kovarianzmatrix dient bei der Beurteilung von Schätzern als Effizienzkriterium. Im Allgemeinen gilt, dass sich die Effizienz eines Parameterschätzers anhand der „Größe“ seiner Varianz-Kovarianzmatrix messen lässt. Es gilt: Je „kleiner“ die Varianz-Kovarianzmatrix, desto „größer“ die Effizienz des Schätzers.
Matrixnotation für die Varianz einer Linearkombination[Bearbeiten | Quelltext bearbeiten]
Es sei ein Spaltenvektor von Zufallsvariablen , und ein Spaltenvektor bestehend aus Skalaren . Dies bedeutet, dass eine Linearkombination dieser Zufallsvariablen ist, wobei die Transponierte von bezeichnet. Sei die Varianz-Kovarianzmatrix von . Die Varianz von ist dann gegeben durch:[47]
Verwandte Maßzahlen[Bearbeiten | Quelltext bearbeiten]
Fasst man die Varianz als Streuungsmaß der Verteilung einer Zufallsvariablen auf, so ist sie mit den folgenden Streuungsmaßen verwandt:
- Variationskoeffizient: Der Variationskoeffizient ist das Verhältnis von Standardabweichung und Erwartungswert und damit ein dimensionsloses Streuungsmaß.
- Quantilabstand: Der Quantilabstand zum Parameter gibt an, wie weit das - und das -Quantil voneinander entfernt sind.
- Mittlere absolute Abweichung: Die mittlere absolute Abweichung ist das erste absolute zentrale Moment.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Variance. In: MathWorld (englisch).
- Ausführliche Berechnungen für den diskreten und stetigen Fall auf mathebibel.de.
Literatur[Bearbeiten | Quelltext bearbeiten]
- George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore, ISBN 978-0-471-62414-1, second edition 1988.
- Ludwig Fahrmeir u. a.: Statistik: Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer-Verlag, 2016, ISBN 978-3-662-50371-3.
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Die Verwendung des Varianzoperators hebt die Berechnungsoperationen hervor. Mit ihm lässt sich die Gültigkeit bestimmter Rechenoperationen besser ausdrücken.
- ↑ Bei einer symmetrischen Verteilung mit dem Symmetriezentrum gilt – falls der Erwartungswert existiert – . Ein Beispiel einer bezüglich symmetrischen Verteilung, für die der Erwartungswert nicht existiert, ist die Standard-Cauchy-Verteilung.
- ↑ Weitere Vorteile des Quadrierens sind zum einen, dass kleine Abweichungen weniger stark gewichtet werden als große Abweichungen, und zum anderen, dass die erste Ableitung eine lineare Funktion ist, was bei Optimierungsüberlegungen von Vorteil ist.
- ↑ Mit der Bezeichnung „Träger“ und dem Zeichen bezeichnet man die Menge aller möglichen Ausprägungen beziehungsweise Realisierungen einer Zufallsvariablen.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Patrick Billingsley: Probability and Measure. 3. Aufl., Wiley, 1995, S. 274 ff.
- ↑ Otfried Beyer, Horst Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik. 1976, S. 53.
- ↑ Brockhaus: Brockhaus, Naturwissenschaften und Technik – Sonderausgabe. 1989, S. 188.
- ↑ Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 3: Vektoranalysis, Wahrscheinlichkeitsrechnung, Mathematische Statistik, Fehler- und Ausgleichsrechnung. 1994, S. 338.
- ↑ Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. 2016, S. 160.
- ↑ Ludwig von Auer: Ökonometrie. Eine Einführung. Springer, ISBN 978-3-642-40209-8, 6. durchges. u. aktualisierte Aufl. 2013, S. 28.
- ↑ Volker Heun: Grundlegende Algorithmen. Einführung in den Entwurf und die Analyse effizienter Algorithmen. 2. Auflage. 2003, S. 108.
- ↑ Gerhard Hübner: Stochastik. Eine anwendungsorientierte Einführung für Informatiker, Ingenieure und Mathematiker. 3. Auflage, 2002, S. 103.
- ↑ Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 231.
- ↑ Von Auer: Ökonometrie. Eine Einführung. 6. Auflage. Springer, 2013, ISBN 978-3-642-40209-8, S. 29.
- ↑ Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 283.
- ↑ Ronald Aylmer Fisher: The Correlation between Relatives on the Supposition of Mendelian Inheritance. Trans. Roy. Soc. Edinb. 52: 399–433, 1918.
- ↑ Lothar Sachs: Statistische Auswertungsmethoden. 1968, 1. Auflage, S. 436.
- ↑ Otfried Beyer, Horst Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik. 1976, S. 58.
- ↑ Otfried Beyer, Horst Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik. 1976, S. 101.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore, ISBN 978-0-471-62414-1, second edition 1988, S. 40.
- ↑ Hans-Otto Georgii: Einführung in die Wahrscheinlichkeitstheorie und Statistik, ISBN 978-3-11-035970-1, S. 102 (abgerufen über De Gruyter Online).
- ↑ Hans-Heinz Wolpers: Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik. S. 20.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore, ISBN 978-0-471-62414-1, second edition 1988, S. 40.
- ↑ W. Zucchini, A. Schlegel, O. Nenadíc, S. Sperlich: Statistik für Bachelor- und Masterstudenten. Springer, 2009, ISBN 978-3-540-88986-1, S. 121.
- ↑ W. Zucchini, A. Schlegel, O. Nenadíc, S. Sperlich: Statistik für Bachelor- und Masterstudenten. Springer, 2009, ISBN 978-3-540-88986-1, S. 123.
- ↑ a b Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 232.
- ↑ Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 254.
- ↑ Wolfgang Viertl, Reinhard Karl: Einführung in die Stochastik: Mit Elementen der Bayes-Statistik und der Analyse unscharfer Information. S. 49.
- ↑ Ansgar Steland: Basiswissen Statistik. Springer, 2016, ISBN 978-3-662-49948-1, S. 116, eingeschränkte Vorschau in der Google-Buchsuche.
- ↑ a b Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 233.
- ↑ Gerhard Hübner: Stochastik. Eine anwendungsorientierte Einführung für Informatiker, Ingenieure und Mathematiker. 3. Auflage, 2002, S. 103.
- ↑ Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 3: Vektoranalysis, Wahrscheinlichkeitsrechnung, Mathematische Statistik, Fehler- und Ausgleichsrechnung. 1994, S. 338.
- ↑ Hans-Otto Georgii: Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7, S. 108, doi:10.1515/9783110215274.
- ↑ Körpergröße der Deutschen. Statistik des Sozio-oekonomischen Panels (SOEP) 2006, aufbereitet durch statista.org.
- ↑ Klenke: Wahrscheinlichkeitstheorie. 2013, S. 106.
- ↑ Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2016, ISBN 978-3-662-50371-3, S. 329.
- ↑ L. Kruschwitz, S. Husmann: Finanzierung und Investition. S. 471.
- ↑ Otfried Beyer, Horst Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik. 1976, S. 86.
- ↑ Irénée-Jules Bienaymé: Considérations à l’appui de la découverte de Laplace sur la loi de probabilité dans la méthode des moindres carrés. In: Comptes rendus de l’Académie des sciences Paris. 37, 1853, S. 309–317.
- ↑ Michel Loeve: Probability Theory (= Graduate Texts in Mathematics. Volume 45). 4. Auflage, Springer-Verlag, 1977, ISBN 3-540-90210-4, S. 12.
- ↑ Leo A. Goodman: On the exact variance of products. In: Journal of the American Statistical Association. Dezember 1960, S. 708–713, doi:10.2307/2281592.
- ↑ Wolfgang Kohn: Statistik: Datenanalyse und Wahrscheinlichkeitsrechnung. S. 250.
- ↑ Otfried Beyer, Horst Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik. 1976, S. 97.
- ↑ Georg Neuhaus: Grundkurs Stochastik. S. 290.
- ↑ Jeffrey M. Wooldrige: Introductory Econometrics: A Modern Approach. 5. Auflage, 2012, S. 736.
- ↑ Toni C. Stocker, Ingo Steinke: Statistik: Grundlagen und Methodik. de Gruyter Oldenbourg, Berlin 2017, ISBN 978-3-11-035388-4, S. 319.
- ↑ Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2, S. 646.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore, ISBN 978-0-471-62414-1, second edition 1988, S. 43.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore, ISBN 978-0-471-62414-1, second edition 1988, S. 43.
- ↑ Wilfried Hausmann, Kathrin Diener, Joachim Käsler: Derivate, Arbitrage und Portfolio-Selection: Stochastische Finanzmarktmodelle und ihre Anwendungen. 2002, S. 15.
- ↑ Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Brian Marx: Regression: Models, Methods and Applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2, S. 647.










































![{\displaystyle {\begin{aligned}\operatorname {Var} [\cdot ]&\colon \chi _{1}\to \mathbb {R} _{+}\cup \{\infty \}\\\operatorname {Var} [F]&=\int (x-\mu (F))^{2}\mathrm {d} F(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/968332dcc69da6bf21931c6c49cfc4a44c696997)

![{\displaystyle \operatorname {Var} \left[X\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d502573c85871695e256cef491cfd85b2a724e6e)


















![{\displaystyle \operatorname {Var} (X)=\int _{-\infty }^{\infty }(x-\mathbb {E} [X])^{2}f(x)\,\mathrm {d} x\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9b2f8467abf930b6e6bb90eb830c77f490a9c34)
![{\displaystyle \mathbb {E} [X]=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b152000fbdf165eb28e866312a5f4cec045327a)










![{\displaystyle \operatorname {Var} (Y)=\mathbb {E} \left[\operatorname {Var} [Y\mid X]\right]+\operatorname {Var} \left[\mathbb {E} [Y\mid X]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a153864b7bd9d33de8cbdc789aa73f6af1e2d842)


![{\displaystyle \operatorname {Var} (Y)=\mathbb {E} \left[\operatorname {Var} [Y\mid {\mathcal {G}}]\right]+\operatorname {Var} \left[\mathbb {E} [Y\mid {\mathcal {G}}]\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2766ace5375ff49b169f85aafe817e5955b8c40)

























































































































































![{\displaystyle \mathbb {E} \left(X^{2}\right)=\int _{-\infty }^{\infty }x^{2}\cdot f(x)\,\mathrm {d} x=\int _{1}^{e}x^{2}\cdot {\frac {1}{x}}\,\mathrm {d} x=\left[{\frac {x^{2}}{2}}\right]_{1}^{e}={\frac {e^{2}}{2}}-{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447e21ab3e3f0c331cd1fb73dd726ae2d705854e)




































