Pythagoras in der Schmiede

Pythagoras in der Schmiede ist eine antike Legende, die beschreibt, wie Pythagoras in einer Schmiede entdeckte, dass gleichzeitige Hammerschläge wohlklingende Töne erzeugten, wenn die Gewichte der Hämmer in bestimmten ganzzahligen Verhältnissen standen. Diese Beobachtung habe ihn zu Experimenten an der schwingenden Saite eines Monochords geführt, die zur Grundlage für die musiktheoretische Beschreibung von Intervallen wurden. Mit den auf diesem Weg gewonnenen Erkenntnissen habe Pythagoras die Musiktheorie begründet. Die Legende hatte zur Folge, dass Pythagoras in der römischen Kaiserzeit und im Mittelalter pauschal als Erfinder „der Musik“ bezeichnet wurde, womit die Musiktheorie gemeint war.
Die Legende ist erst in der römischen Kaiserzeit in griechischer Sprache bezeugt, ältere Quellen sind nicht bekannt und möglicherweise verloren gegangen. Im Laufe der Jahrhunderte wurde die Erzählung abgewandelt. Erst im 17. Jahrhundert konnte gezeigt werden, dass die Darstellung der Legende nicht zutreffen kann, weil die Tonhöhe beim Hämmern kaum vom Gewicht des Hammers abhängt und die Schwingungen des Hammers selbst praktisch unhörbar sind. Dennoch wird die Legende auch in neueren Veröffentlichungen noch wie ein glaubwürdiger Bericht behandelt.
Unabhängig von der Frage, wie und durch wen die Pythagoras zugeschriebene Entdeckung von musikalischen Zahlenverhältnissen tatsächlich erfolgt ist, handelt es sich bei der Formulierung dieser Zahlenverhältnisse um die erste überlieferte mathematische Beschreibung eines physikalischen Sachverhalts, für deren Richtigkeit experimentelle Beobachtungen als Beleg angeführt wurden.[1]
Inhalt der Legende[Bearbeiten | Quelltext bearbeiten]
Der ältesten überlieferten Version[2] der Legende zufolge hat Pythagoras, der im 6. Jahrhundert v. Chr. lebte, ein Hilfsmittel gesucht, mit dem akustische Wahrnehmungen gemessen werden können so wie geometrische Größen mit dem Zirkel oder Gewichte mit der Waage. Als er an einer Schmiede vorbeikam, wo vier (nach einer späteren Version fünf) Handwerker mit Hämmern bei der Arbeit waren, bemerkte er, dass die einzelnen Schläge Töne unterschiedlicher Tonhöhe hervorriefen, die paarweise Harmonien ergaben. Dabei konnte er Oktave, Quinte und Quarte unterscheiden. Nur ein Paar, welches das Intervall zwischen Quarte und Quinte (große Sekunde) ergab, empfand er als dissonant. Darauf lief er freudig in die Schmiede, um Versuche anzustellen. Dabei fand er heraus, dass der Unterschied in der Tonhöhe weder von der Gestalt des Hammers noch von der Lage des geschlagenen Eisens oder der Kraft des Schlags abhängt. Vielmehr konnte er die Tonhöhen den Gewichten der Hämmer zuordnen, die er genau maß. Darauf kehrte er nach Hause zurück, um dort die Experimente fortzusetzen.
An einem Pflock, der schräg über die Ecke an den Wänden befestigt war, hängte er der Reihe nach vier gleich lange, gleich starke und gleich gedrehte Saiten auf, die er unten durch Anbinden unterschiedlicher Gewichte beschwerte. Dann schlug er die Saiten paarweise an, wobei die gleichen Harmonien erklangen wie in der Schmiede. Die mit zwölf Gewichtseinheiten am stärksten beschwerte Saite ergab mit der am geringsten belasteten, an der sechs Gewichtseinheiten hingen, eine Oktave. So zeigte sich, dass die Oktave auf dem Verhältnis 12 : 6, also 2 : 1 beruht. Die gespannteste Saite ergab mit der zweitlockersten (acht Gewichtseinheiten) eine Quinte, mit der zweitstraffsten (neun Gewichtseinheiten) eine Quarte. Daraus folgte, dass die Quinte auf dem Verhältnis 12 : 8, also 3 : 2 beruht, die Quarte auf dem Verhältnis 12 : 9, also 4 : 3. Für das Verhältnis der zweitstraffsten Saite zur lockersten ergab sich wiederum mit 9 : 6, also 3 : 2, eine Quinte, für das der zweitlockersten zur lockersten mit 8 : 6, also 4 : 3, eine Quarte. Für das dissonante Intervall zwischen Quinte und Quarte zeigte sich, dass es auf dem Verhältnis 9 : 8 beruht, was mit den schon in der Schmiede durchgeführten Gewichtsmessungen übereinstimmte. Die Oktave erwies sich als das Produkt von Quinte und Quarte:
Dann dehnte Pythagoras den Versuch auf verschiedene Instrumente aus, experimentierte mit Gefäßen, Flöten, Triangeln, dem Monochord usw.; dabei fand er immer die gleichen Zahlenverhältnisse. Schließlich führte er die seither geläufigen Benennungen für die relativen Tonhöhen ein.
Weitere Überlieferungen[Bearbeiten | Quelltext bearbeiten]
Mit der Erfindung des Monochords zur Untersuchung und Demonstration der Zusammenklänge von Saitenpaaren mit verschiedenen ganzzahligen Längenverhältnissen soll Pythagoras ein bequemes Mittel zum Aufzeigen der von ihm entdeckten mathematischen Grundlage der Musiktheorie eingeführt haben. Das Monochord – altgriechisch κανών kanōn, lateinisch regula genannt – ist ein Resonanzkasten, über den eine Saite gespannt ist. Auf dem Kasten ist eine Maßeinteilung angebracht. Das Gerät ist mit einem verschiebbaren Steg ausgestattet, durch dessen Verschiebung man die schwingende Länge der Saite teilen kann; anhand der Maßeinteilung lässt sich die Teilung genau bestimmen. Damit wird eine Messung der Intervalle möglich. Trotz des Namens „Monochord“, der „einsaitig“ bedeutet, gab es auch mehrsaitige Monochorde, mit denen man die Intervalle simultan zum Klingen bringen konnte. Allerdings ist unklar, wann das Monochord erfunden wurde. Walter Burkert datiert diese Errungenschaft erst nach der Zeit des Aristoteles, der das Gerät anscheinend noch nicht kannte; demnach wurde es erst lange nach Pythagoras' Tod eingeführt.[3] Leonid Zhmud hingegen meint, Pythagoras habe sein Experiment, das zur Entdeckung der Zahlenverhältnisse führte, wahrscheinlich mit dem Monochord durchgeführt.[4]
Hippasos von Metapont, ein Pythagoreer der Frühzeit (spätes 6. und frühes 5. Jahrhundert v. Chr.), hat quantitative Untersuchungen zu musikalischen Intervallen durchgeführt. Das Hippasos zugeschriebene Experiment mit verschieden dicken frei schwingenden Kreisplatten ist im Gegensatz zu den angeblichen Versuchen des Pythagoras physikalisch korrekt. Ob Archytas von Tarent, ein bedeutender Pythagoreer des 5./4. Jahrhunderts v. Chr., einschlägige Experimente durchgeführt hat, ist unklar. Vermutlich war er in der Musik eher Theoretiker als Praktiker, doch nahm er auf akustische Beobachtungen seiner Vorgänger Bezug. Die musikalischen Beispiele, die er zur Stützung seiner akustischen Theorie anführt, betreffen Blasinstrumente; Versuche mit Saiteninstrumenten oder einzelnen Saiten führt er nicht an. Archytas ging von der falschen Hypothese aus, dass die Tonhöhe von der Ausbreitungsgeschwindigkeit des Schalls und der Wucht des Stoßes auf den Klangkörper abhängt; in Wirklichkeit ist die Schallgeschwindigkeit in einem gegebenen Medium konstant und die Wucht beeinflusst nur die Lautstärke.[5]
Interpretation der Legende[Bearbeiten | Quelltext bearbeiten]
Walter Burkert ist der Ansicht, dass die Legende trotz der physikalischen Unmöglichkeit nicht als willkürliche Erfindung zu betrachten sei, sondern einen Sinn habe, der in der griechischen Mythologie zu finden sei. Die Idäischen Daktylen, die mythischen Erfinder der Schmiedekunst, waren einem Mythos zufolge auch die Erfinder der Musik. Von einem Zusammenhang zwischen Schmiedekunst und Musik ging somit offenbar schon eine sehr alte Überlieferung aus, in der die mythischen Schmiede als Kenner des Geheimnisses der magischen Musik dargestellt wurden. Burkert sieht in der Legende von Pythagoras in der Schmiede eine späte Umformung und Rationalisierung des uralten Daktylen-Mythos: In der Pythagoras-Legende erscheinen die Schmiede nicht mehr als Besitzer alten magischen Wissens, sondern sie werden, ohne es zu wollen, zu – wenngleich unwissenden – „Lehrmeistern“ des Pythagoras.[6]
Im Frühmittelalter bezeichnete Isidor von Sevilla den biblischen Schmied Tubal als den Erfinder der Musik; darin folgten ihm spätere Autoren. In dieser Überlieferung zeigt sich wiederum die Vorstellung einer Beziehung zwischen Schmiedekunst und Musik, die auch in außereuropäischen Mythen und Sagen vorkommt.[7] Tubal war Halbbruder des Jubal, der als Urvater aller Musiker angesehen wurde. Beide waren Söhne des Lamech und somit Enkel des Kain. In manchen christlichen Überlieferungen des Mittelalters wurde der seinen Bruder Tubal beobachtende Jubal mit Pythagoras gleichgesetzt.[8]
Eine andere Erklärung schlägt Jørgen Raasted vor, dem Leonid Zhmud folgt. Raasteds Hypothese besagt, dass der Ausgangspunkt der Legendenbildung ein Bericht über Experimente des Hippasos gewesen sei. Hippasos verwendete Gefäße, die sphaírai genannt wurden. Dieses Wort sei durch ein Schreiberversehen mit sphýrai (Hämmer) verwechselt worden, und statt Hippasos' Namen sei der des Pythagoras als Urheber der Versuche eingesetzt worden. Daraus sei dann die Schmiedelegende entstanden.[9]
Grundlage der Musiktheorie[Bearbeiten | Quelltext bearbeiten]
Die ganzen Zahlen 6, 8, 9 und 12 entsprechen bezogen auf den tiefsten Ton (Zahl 12) den reinen Intervallen Quarte (Zahl 9), Quinte (Zahl 8) und Oktave (Zahl 6) nach oben:
| Ganze Zahl | Verhältnis zur größten Zahl 12 |
Verhältnis, gekürzt |
Verhältniszahl | Intervallbezeichnung |
|---|---|---|---|---|
| 12 | 12:12 | 1:1 | 1,000 | Prime |
| 9 | 9:12 | 3:4 | 0,750 | Quarte |
| 8 | 8:12 | 2:3 | 0,667 | Quinte |
| 6 | 6:12 | 1:2 | 0,500 | Oktave |
Solche reinen Intervalle werden vom menschlichen Ohr als schwebungsfrei wahrgenommen, da die Lautstärke der Töne nicht variiert. In Notenschrift können diese vier pythagoreischen Töne zum Beispiel mit der Tonfolge c′ – f′ – g′ – c″ ausgedrückt werden:

Wird diese Tonfolge nicht vom tiefsten, sondern vom höchsten Ton (Zahl 6) aus betrachtet, ergeben sich ebenfalls eine Quarte (Zahl 8), eine Quinte (Zahl 9) und eine Oktave (Zahl 12) – in diesem Fall allerdings nach unten:
| Ganze Zahl | Verhältnis zur kleinsten Zahl 6 |
Verhältnis, gekürzt |
Verhältniszahl | Intervallbezeichnung |
|---|---|---|---|---|
| 6 | 6:6 | 1:1 | 1,000 | Prime |
| 8 | 8:6 | 4:3 | 1,333 | Quarte |
| 9 | 9:6 | 3:2 | 1,500 | Quinte |
| 12 | 12:6 | 2:1 | 2,000 | Oktave |
Die Quinte und die Oktave tauchen in Bezug auf den Grundton zwar auch bei Naturtonreihen auf, nicht jedoch die Quarte oder deren Oktavierungen. Dieser Quartton kommt bei den schon in der Antike bekannten ventillosen Blechblasinstrumenten und bei Flageoletttönen von Saiteninstrumenten nicht vor.
Bedeutung für die spätere Weiterentwicklung der Tonsysteme[Bearbeiten | Quelltext bearbeiten]
Die weitere Untersuchung von Intervallen bestehend aus Oktaven, Quinten und Quarten und deren Vielfachen führte schließlich von diatonischen Tonleitern mit sieben verschiedenen Tönen (Heptatonik) in Pythagoreischer Stimmung zu einer chromatischen Tonleiter mit zwölf Tönen. Dabei störten die Pythagoreischen Wolfsquinten: Statt der reinen Quinten As – Es und Des – As erklangen die um das pythagoreisches Komma verstimmten Quinten Gis — Es und Cis — As.
Mit dem Aufkommen der Mehrstimmigkeit in der zweiten Hälfte des 15. Jahrhunderts wurde neben der Oktave und Quinte auch die reine Terz für die Dur- und Molldreiklänge entscheidend. Diese Stimmung war zwar auf einer zwölfstufigen Tastatur nicht realisierbar, konnte aber gut in der mitteltönigen Stimmung verwirklicht werden. Ihr Nachteil war, dass nicht alle Tonarten des Quintenzirkels spielbar waren. Um diesen Mangel zu beheben, wurden die temperierten Stimmungen eingeführt, allerdings mit der Einbuße, dass die reine Terz in manchen Tonarten rauer erklang. Heutzutage sind die meisten Instrumente mit 12 Tasten gleichstufig gestimmt, sodass die Oktaven vollkommen rein, die Quinten fast rein und die Terzen rau erklingen.
Die vier pythagoreischen Töne in der Musik[Bearbeiten | Quelltext bearbeiten]
In der Musik spielen die vier harmonischen pythagoreischen Töne in der Pentatonik, besonders auf der ersten, vierten, fünften und achten Tonstufe von diatonischen Tonleitern (insbesondere bei Dur und Moll) und bei der Komposition von Kadenzen als Grundtöne von Tonika, Subdominante und Dominante eine herausragende Rolle. Diese Tonfolge tritt oft bei Schlusskadenzen mit den entsprechenden Akkorden auf:

Die vier pythagoreischen Töne tauchen in vielen Kompositionen auf. Die ersten Töne der frühmittelalterlichen Antiphonen Ad te levavi und Factus est repente bestehen abgesehen von einigen Verzierungen beziehungsweise Spitzentönen im Wesentlichen aus den vier pythagoreischen Tönen.[10]

Ein weiteres Beispiel ist der Anfang der Passacaglia c-Moll von Johann Sebastian Bach. Das Thema besteht aus fünfzehn Tönen, von denen insgesamt zehn Töne und insbesondere die letzten vier Töne aus der Tonfolge geschöpft wurden.
Widerlegung[Bearbeiten | Quelltext bearbeiten]
Absolute Tonhöhe von Hämmern
Die Eigenfrequenz von Stahlhämmern, die von Menschenhand bewegt werden können, ist meist im Ultraschallbereich und somit unhörbar. Pythagoras kann diese Töne nicht wahrgenommen haben, insbesondere wenn die Hämmer in der Tonhöhe einen Unterschied von einer Oktave aufwiesen.
Tonhöhe in Abhängigkeit vom Hammergewicht
Die Schwingungsfrequenz eines longitudinal frei schwingenden Festkörpers ist in der Regel nicht proportional zu seinem Gewicht beziehungsweise seinem Volumen, wohl aber proportional zur Länge, die sich bei ähnlicher Geometrie nur mit der Kubikwurzel des Volumens ändert.
Für die pythagoreischen Hämmer gelten bei ähnlicher Geometrie also die folgenden Verhältniszahlen (Angaben in willkürlichen Maßeinheiten):
| Gewicht / Volumen |
Verhältniszahl zum größten Hammer |
Hammerkopflänge / Schwingungsfrequenz |
Verhältniszahl zum größten Hammer | |
|---|---|---|---|---|
| 12 | 1,000 | 2,289 | 1,000 | |
| 9 | 0,750 | 2,080 | 0,909 | |
| 8 | 0,667 | 2,000 | 0,874 | |
| 6 | 0,500 | 1,817 | 0,794 |
Tonhöhe in Abhängigkeit von der Saitenspannung
Die Annahme, dass die Schwingungsfrequenz einer Saite proportional zur Spannkraft ist, trifft nicht zu, vielmehr ist die Schwingungsfrequenz proportional zur Quadratwurzel der Spannkraft. Um die Schwingungsfrequenz zu verdoppeln, muss also eine vierfache Zugkraft ausgeübt und somit ein viermal so schweres Gewicht an eine Saite gehängt werden.
Physikalische Betrachtungen[Bearbeiten | Quelltext bearbeiten]
Konsonanz[Bearbeiten | Quelltext bearbeiten]
Ganzzahlige Frequenzverhältnisse[Bearbeiten | Quelltext bearbeiten]
| Ganzzahliges Verhältnis der Frequenzen |
n | Schwebungsfrequenz |
|---|---|---|
| 2:1 | 2 | |
| 3:1 | 3 | |
| 4:1 | 4 | |
| 5:1 | 5 |
Die Tatsache, dass ein Ton mit der Grundfrequenz in Konsonanz zu einem zweiten Ton mit einem ganzzahligen Vielfachen (mit und ) dieser Grundfrequenz steht, ergibt sich zwar schon unmittelbar daraus, dass die Maxima und Minima der Tonschwingungen zeitlich synchron sind, kann aber auch folgendermaßen erklärt werden:
Die Schwebungsfrequenz der beiden gleichzeitig klingenden Töne ergibt sich rechnerisch aus der Differenz der Frequenzen dieser beiden Töne und ist als Kombinationston hörbar:
(siehe Mathematische Beschreibung der Schwebung).
Diese Differenz steht ihrerseits in einem ganzzahligen Verhältnis zur Grundfrequenz :
Für alle ganzzahligen Vielfachen der Grundfrequenz beim zweiten Ton ergeben sich auch ganzzahlige Vielfache für die Schwebungsfrequenz (siehe nebenstehende Tabelle), so dass alle Töne konsonant klingen.
Rationale Frequenzverhältnisse[Bearbeiten | Quelltext bearbeiten]
| Rationales Verhältnis der Frequenzen |
n | Schwebungsfrequenz |
Grundfrequenz |
|---|---|---|---|
| 2:1 | 1 | ||
| 3:2 | 2 | ||
| 4:3 | 3 | ||
| 5:4 | 4 |
Auch für zwei Töne, deren Frequenzen in einem rationalen Verhältnis von zu stehen, gibt es eine Konsonanz. Die Frequenz des zweiten Tones ergibt sich hierbei nach:
Demzufolge ergibt sich für die Schwebungsfrequenz der beiden gleichzeitig klingenden Töne:
Die Grundfrequenz ist also unter dieser Bedingung immer ein ganzzahliges Vielfaches der Schwebungsfrequenz (siehe nebenstehende Tabelle). Daher entsteht ebenfalls keine Dissonanz.
Longitudinale Schwingungen und Eigenfrequenz von Festkörpern[Bearbeiten | Quelltext bearbeiten]
Zur Abschätzung eines Metallklotzes möge ein homogener Quader mit einer maximalen Länge und aus einem Material mit der Schallgeschwindigkeit betrachtet werden. Dieser hat für den Schwingungsmodus entlang seiner längsten Seite (Longitudinalschwingung) mit Schwingungsbäuchen an den beiden Enden und einem Schwingungsknoten in der Mitte die tiefste Eigenfrequenz von[11]
- .
Die Tonhöhe ist also unabhängig von der Masse und der Querschnittsfläche des Quaders, die Querschnittsfläche darf sogar variieren. Ferner spielen auch die Kraft und die Geschwindigkeit beim Anschlagen des Körpers keine Rolle. Zumindest dieser Sachverhalt deckt sich mit der Pythagoras zugeschriebenen Beobachtung, dass die wahrgenommene Tonhöhe nicht von den Händen (und somit den Kräften) der Handwerker abhängig gewesen sei.
Körper mit komplizierterer Geometrie, wie zum Beispiel Glocken, Becher oder Schalen, die eventuell sogar noch mit Flüssigkeiten gefüllt sind, haben Eigenfrequenzen, deren physikalische Beschreibung erheblich aufwendiger ist, da hier nicht nur die Form, sondern auch die Wanddicke oder sogar der Ort des Anschlagens berücksichtigt werden müssen. Hierbei werden unter Umständen auch Transversalschwingungen angeregt und hörbar.
Hämmer[Bearbeiten | Quelltext bearbeiten]

Ein sehr großer Vorschlaghammer (die Schallgeschwindigkeit in Stahl beträgt ungefähr = 5000 Meter pro Sekunde) mit einer Hammerkopflänge = 0,2 Meter hat also eine Eigenfrequenz von 12,5 Kilohertz. Bei einer quadratischen Querschnittsfläche von 0,1 Meter mal 0,1 Meter hätte er bei der Dichte von 7,86 Gramm pro Kubikzentimeter eine ungewöhnlich große Masse von fast 16 Kilogramm. Bereits Frequenzen oberhalb von etwa 15 Kilohertz können von vielen Menschen nicht mehr wahrgenommen werden (siehe Hörfläche); daher ist die Eigenfrequenz selbst eines solch großen Hammers kaum hörbar. Hämmer mit kürzeren Köpfen haben noch höhere Eigenfrequenzen, die daher keinesfalls hörbar sind.
Ambosse[Bearbeiten | Quelltext bearbeiten]
Ein großer Amboss aus Stahl mit einer Länge = 0,5 Meter hat eine Eigenfrequenz von nur 5 Kilohertz und ist somit gut hörbar.
Es gibt Kompositionen, in denen der Komponist die Verwendung von Ambossen als Musikinstrument vorschreibt. Besonders bekannt sind die beiden Opern aus dem Musikdrama Der Ring des Nibelungen von Richard Wagner:
- Das Rheingold, Szene 3, 18 Ambosse in F in drei Oktaven
- Siegfried, 1. Aufzug, Siegfrieds Schmiedelied Nothung! Nothung! Neidliches Schwert!
Materialien mit geringerer Schallgeschwindigkeit als Stahl, wie zum Beispiel Granit oder Messing, erzeugen bei kongruenter Geometrie noch tiefere Frequenzen. Jedenfalls ist von Ambossen in den frühen Überlieferungen und von hörbaren Klängen der Ambosse in den später überlieferten Versionen der Legende nicht die Rede, sondern die Klänge werden immer den Hämmern zugeschrieben.
Metallstäbe[Bearbeiten | Quelltext bearbeiten]


Klangbeispiele von Meißeln mit Schwingungsfrequenzen, die in ganzzahligen Verhältnissen zueinander stehen:
Es ist möglich, Metallstäbe zu vergleichen, wie zum Beispiel Meißel von Steinmetzen oder Spaltkeile zum Steinbrechen, um auf eine ähnliche wie die Pythagoras zugeschriebene Beobachtung zu kommen, dass nämlich die Schwingungsfrequenz von Werkzeugen proportional zu deren Gewicht ist. Wenn die Metallstäbe unter der Vernachlässigung der spitz zulaufenden Werkzeugschneiden alle dieselbe gleichmäßige Querschnittsfläche A, aber verschiedene Längen l haben, ist ihr Gewicht proportional zur Länge und somit auch zur Schwingungsfrequenz, sofern die Metallstäbe durch Schläge entlang der Längsachse zu longitudinalen Schwingungen angeregt werden (Klangbeispiele siehe im Kasten rechts).[12]
Für Biegeschwinger, wie zum Beispiel Stimmgabeln oder die Plättchen von Metallophonen, gelten allerdings andere Bedingungen und Gesetze; daher sind diese Überlegungen nicht auf sie anwendbar.
Saitenschwingungen[Bearbeiten | Quelltext bearbeiten]

Saiten können an zwei Seiten auf jeweils einem Steg fixiert werden. Genau andersherum als bei einem Festkörper mit longitudinalen Schwingungen stellen die beiden Stege die Randbedingungen für zwei Schwingungsknoten her; daher befindet sich der Schwingungsbauch in der Mitte.
Die Eigenfrequenz und somit die Tonhöhe von Saiten mit der Länge sind nicht proportional zur Spannkraft , sondern zur Quadratwurzel der Spannkraft. Außerdem nimmt die Frequenz bei höherem Zuggewicht und somit höherer Spannkraft zu und nicht ab:[13]
Nichtsdestoweniger ist die Schwingungsfrequenz bei konstanter Spannkraft streng umgekehrt proportional zur Länge der Saite, was mit dem – angeblich von Pythagoras erfundenen – Monochord direkt nachgewiesen werden kann.
Rezeption[Bearbeiten | Quelltext bearbeiten]

Antike[Bearbeiten | Quelltext bearbeiten]
Die früheste Erwähnung von Pythagoras' Entdeckung der mathematischen Grundlage der musikalischen Intervalle findet sich bei dem Platoniker Xenokrates (4. Jahrhundert v. Chr.); da es sich nur um ein Zitat aus einem verlorenen Werk dieses Denkers handelt, ist unklar, ob er die Schmiedelegende kannte.[14] Im 4. Jahrhundert v. Chr. wurde auch schon – allerdings ohne Bezugnahme auf die Pythagoras-Legende – Kritik an der pythagoreischen Zahlentheorie der Intervalle geäußert; der Philosoph und Musiktheoretiker Aristoxenos hielt sie für falsch.

Die älteste überlieferte Version der Legende präsentiert – Jahrhunderte nach der Zeit des Pythagoras – der Neupythagoreer Nikomachos von Gerasa, der im 1. oder 2. Jahrhundert nach Christus die Geschichte in seinem Harmonikon encheiridion („Handbuch der Harmonielehre“) festgehalten hat. Er beruft sich für seine Darstellung der Zahlenverhältnisse in der Harmonielehre auf den Philosophen Philolaos, einen Pythagoreer des 5. Jahrhunderts vor Christus.[15]
Der berühmte Mathematiker und Musiktheoretiker Ptolemaios (2. Jahrhundert) kannte die von der Legende überlieferte Gewichtsmethode und lehnte sie ab; er hatte allerdings nicht die Falschheit der Gewichtsexperimente erkannt, sondern bemängelte nur ihre Ungenauigkeiten im Vergleich mit den genauen Messungen am Monochord.[16] Wahrscheinlich bezog er seine Kenntnis der legendenhaften Überlieferung nicht von Nikomachos, sondern aus einer älteren, heute verlorenen Quelle.[17]
Der chronologisch schwer einzuordnende kaiserzeitliche Musiktheoretiker Gaudentios schilderte in seiner Harmonikḗ eisagōgḗ („Einführung in die Harmonie“) die Legende in einer Fassung, die etwas kürzer ist als die des Nikomachos. Der Neuplatoniker Iamblichos, der im späten 3. und frühen 4. Jahrhundert als Philosophielehrer tätig war, verfasste eine Pythagoras-Biographie mit dem Titel Über das pythagoreische Leben, worin er die Schmiedelegende in der Version des Nikomachos wiedergab.
In der ersten Hälfte des 5. Jahrhunderts ging der Schriftsteller Macrobius in seinem Kommentar zu Ciceros Somnium Scipionis ausführlich auf die Schmiedelegende ein, die er ähnlich wie Nikomachos schilderte.[18]

Die stärkste Nachwirkung unter den antiken Musiktheoretikern, welche die Erzählung aufgriffen, erzielte Boethius mit seinem im frühen 6. Jahrhundert verfassten Lehrbuch De institutione musica („Einführung in die Musik“), in dem er die Erkenntnisbemühungen des Pythagoras zunächst in der Schmiede und dann zu Hause schildert.[19] Ob er dabei von der Darstellung des Nikomachos oder von einer anderen Quelle ausging, ist unklar. Im Unterschied zur gesamten älteren Überlieferung berichtet er von fünf Hämmern, statt wie die früheren Autoren vier Hämmer anzunehmen. Er behauptet, den fünften Hammer habe Pythagoras verworfen, weil er mit allen anderen Hämmern eine Dissonanz ergeben habe. Nach Boethius' Darstellung (wie schon bei Macrobius) überprüfte Pythagoras seine erste Vermutung, der Klangunterschied beruhe auf unterschiedlicher Kraft in den Armen der Männer, indem er die Schmiede die Hämmer tauschen ließ, was zur Widerlegung führte. Über die Versuche im Hause des Pythagoras schreibt Boethius, der Philosoph habe zuerst an die Saiten gleich schwere Gewichte gehängt wie die der Hämmer in der Schmiede und dann mit Rohren und Bechern experimentiert, wobei alle Versuche zu denselben Ergebnissen geführt hätten wie die ersten mit den Hämmern. Anhand der Legende thematisiert Boethius die wissenschafts- und erkenntnistheoretische Frage nach der Zuverlässigkeit von Sinneswahrnehmungen. Wesentlich ist dabei der Umstand, dass Pythagoras zunächst durch Sinneswahrnehmung zu seiner Fragestellung und zur Hypothesenbildung angeregt wurde und durch empirische Überprüfung von Hypothesen zu unumstößlicher Gewissheit gelangte. Der Erkenntnisweg führte von der Sinneswahrnehmung zur ersten Hypothese, die sich als irrig erwies, dann zur Bildung einer richtigen Meinung und schließlich zu deren Verifizierung. Boethius anerkennt die Notwendigkeit und den Wert der Sinneswahrnehmung und der Meinungsbildung auf dem Weg zur Einsicht, obwohl er als Platoniker der Sinneswahrnehmung wegen ihrer Irrtumsanfälligkeit prinzipiell misstraut. Wirkliches Wissen ergibt sich für ihn erst, wenn die Gesetzmäßigkeit erfasst ist, womit der Forscher sich von seiner anfänglichen Abhängigkeit von der unzuverlässigen Sinneswahrnehmung emanzipiert. Das Urteil des Forschers darf nicht bloß als Sinnesurteil auf der empirischen Erfahrung beruhen, sondern es darf erst gefällt werden, wenn er durch Überlegungen eine Regel gefunden hat, die es ihm ermöglicht, sich jenseits des Bereichs möglicher Sinnestäuschung zu positionieren.[20]
Im 6. Jahrhundert schrieb der Gelehrte Cassiodor in seinen Institutiones, Gaudentios habe in seinem Bericht über die Schmiedelegende die Anfänge "der Musik" auf Pythagoras zurückgeführt. Gemeint war die Musiktheorie, wie schon bei Iamblichos, der ebenfalls mit Bezug auf die Schmiedeerzählung und die dort beschriebenen Experimente Pythagoras als Erfinder "der Musik" bezeichnet hatte.[21]
Mittelalter[Bearbeiten | Quelltext bearbeiten]
Im Frühmittelalter erwähnte Isidor von Sevilla in seinen Etymologien, die zu einem maßgeblichen Nachschlagewerk der mittelalterlichen Gebildeten wurden, die Schmiedelegende kurz, wobei er Cassiodors Formulierung übernahm und ebenfalls Pythagoras als Erfinder der Musik bezeichnete.[22] Da Cassiodor und Isidor im Mittelalter erstrangige Autoritäten waren, verbreitete sich die Vorstellung, Pythagoras habe das Grundgesetz der Musik entdeckt und sei somit deren Begründer gewesen. Trotz solcher pauschaler Formulierungen gingen die mittelalterlichen Musiktheoretiker aber davon aus, dass es Musik schon vor Pythagoras gegeben hatte und dass mit der "Erfindung der Musik" die Entdeckung ihrer Prinzipien gemeint war.[23]
Im 9. Jahrhundert berichtete der Musikwissenschaftler Aurelian von Réomé in seiner Musica disciplina („Musiklehre“) von der Legende. Aurelians Darstellung folgte im 10. Jahrhundert Regino von Prüm in seiner Schrift De harmonica institutione („Einführung in die Harmonielehre“). Beide legten Wert auf die Feststellung, dass Pythagoras durch eine göttliche Fügung die Gelegenheit erhalten habe, in der Schmiede seine Entdeckung zu machen.[24] Schon in der Antike hatten Nikomachos und Iamblichos von einer daimonischen Fügung gesprochen, Boethius hatte daraus einen göttlichen Ratschluss gemacht.
Im 11. Jahrhundert wurde der Legendenstoff in den Carmina Cantabrigiensia verarbeitet.[25]

In der ersten Hälfte des 11. Jahrhunderts erzählte Guido von Arezzo, der berühmteste Musiktheoretiker des Mittelalters, im letzten Kapitel seines Micrologus die Schmiedelegende, wobei er von der Version des Boethius, den er namentlich nannte, ausging. Einleitend bemerkte Guido: Auch würde wohl niemals ein Mensch etwas Bestimmtes über diese Kunst (die Musik) erforscht haben, wenn nicht schließlich die göttliche Güte auf ihren Wink das nachfolgende Ereignis herbeigeführt hätte. Dass die Hämmer 12, 9, 8 und 6 Gewichtseinheiten wogen und so den Wohlklang erzeugten, führte er auf Gottes Fügung zurück.[26] Er erwähnte auch, dass Pythagoras von seiner Entdeckung ausgehend das Monochord erfunden habe, ging aber dabei nicht näher auf dessen Eigenschaften ein.
Das Werk De musica des Johannes Cotto (auch unter den Namen John Cotton oder Johannes Afflighemensis bekannt) wurde um 1250 von einem anonymen Buchmaler der Zisterzienserabtei Aldersbach mit der Schmiedeszene illustriert.[27]
Zu den mittelalterlichen Musiktheoretikern, welche die Schmiedelegende nach der Version des Boethius erzählten, gehören ferner der im späten 13. und frühen 14. Jahrhundert tätige Juan Gil de Zámora (Johannes Aegidius von Zamora), im 14. Jahrhundert Johannes de Muris und Simon Tunstede, im 15. Jahrhundert an der Schwelle zur Neuzeit Adam von Fulda.
Als Gegner der pythagoreischen Auffassung, wonach die Konsonanzen auf bestimmten Zahlenverhältnissen beruhen, trat im 13. Jahrhundert Johannes de Grocheio hervor, der von einer aristotelischen Sichtweise ausging. Er stellte zwar ausdrücklich fest, dass Pythagoras die Prinzipien der Musik entdeckt habe, und erzählte die Schmiedelegende mit Berufung auf Boethius, den er für vertrauenswürdig hielt, doch verwarf er die pythagoreische Konsonanzlehre, die er auf eine bloß metaphorische Redeweise reduzieren wollte.[28]
Frühe Neuzeit[Bearbeiten | Quelltext bearbeiten]


Franchino Gaffurio veröffentlichte 1480 in Neapel sein Werk Theoricum opus musice discipline („Theoretische Musiklehre“), das 1492 in einer überarbeiteten Fassung unter dem Titel Theorica musice („Musiktheorie“) erschien. Darin präsentierte er eine Version der Schmiedelegende, die an Ausführlichkeit alle früheren Darstellungen übertraf. Er ging von der Fassung des Boethius aus und fügte einen sechsten Hammer hinzu, um möglichst alle Töne der Oktave in der Erzählung unterzubringen. In vier bildlichen Darstellungen präsentierte er Musikinstrumente bzw. Klangerzeuger mit jeweils sechs harmonischen Tönen und gab dazu die den Tönen zugeordneten Zahlen 4, 6, 8, 9, 12 und 16 in der Beschriftung an. Den vier traditionellen Verhältniszahlen der Legende (6, 8, 9 und 12) fügte er die 4 und die 16 hinzu, die einen Ton um eine Quinte tiefer und einen weiteren Ton um eine Quarte höher repräsentieren. Die gesamte Tonfolge erstreckt sich also nun nicht nur über eine, sondern über zwei Oktaven. Diese Zahlen entsprechen zum Beispiel den Tönen f – c' – f' – g' – c" – f":
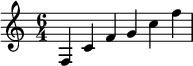
Der Maler Erhard Sanßdorffer wurde im Jahr 1546 damit beauftragt, im hessischen Schloss Büdingen ein Fresko zu gestalten, das gut erhalten ist und die Musikgeschichte ausgehend von der Schmiede des Pythagoras wie ein Kompendium darstellt.[29]
Auch Gioseffo Zarlino erzählte die Legende in seiner Schrift Le istitutioni harmoniche („Die Grundlagen der Harmonie“), die er im Jahr 1558 publizierte; dabei legte er wie Gaffurio die Darstellung des Boethius zugrunde.[30]
Der Musiktheoretiker Vincenzo Galilei, der Vater von Galileo Galilei, veröffentlichte 1589 seine Streitschrift Discorso intorno all’opere di messer Gioseffo Zarlino („Abhandlung über die Werke des Herrn Gioseffo Zarlino“), die gegen die Ansichten seines Lehrers Zarlino gerichtet war. Darin wies er darauf hin, dass die Angaben der Legende über die Belastung von Saiten mit Gewichten nicht zutreffen.[31]

1626 erschien im Thesaurus philopoliticus von Daniel Meisner ein Kupferstich von Eberhard Kieser mit dem Titel Duynkirchen, auf dem nur drei Schmiede an einem Amboss zu sehen sind. Der lateinisch und deutsch abgefasste Bildtext lautet:[32]
- Triplicibus percussa sonat varie ictibus incus.
- Musica Pythagoras struit hinc fundamina princ(eps).
- Der Amboß von drey Hämmern klingt, darauß dreyerley thon entspringt.
- Pythagoras hie die Music findt, das hett kein Eselskopff gekönt.
Einige Jahre später wurde der Sachverhalt definitiv geklärt, nachdem Galileo Galilei und Marin Mersenne die Gesetze für die Schwingungen von Saiten entdeckt hatten. Mersenne veröffentlichte 1636 seine Harmonie universelle, in der er den physikalischen Fehler in der Legende darlegte: Die Schwingungsfrequenz ist nicht zur Spannkraft, sondern zu deren Quadratwurzel proportional.
Mehrere Komponisten verarbeiteten den Stoff in ihren Werken, darunter am Ende des 17. Jahrhunderts Georg Muffat[33] und Rupert Ignaz Mayr.[34]
Moderne[Bearbeiten | Quelltext bearbeiten]
Noch im 19. Jahrhundert ging Hegel in seinen Vorlesungen über die Geschichte der Philosophie von der physikalischen Richtigkeit der angeblichen Messungen, die in der Pythagoras-Legende mitgeteilt werden, aus.[35]
Werner Heisenberg betonte in einem erstmals 1937 veröffentlichten Aufsatz, die pythagoreische „Entdeckung der mathematischen Bedingtheit der Harmonie“ beruhe auf „dem Gedanken an die sinngebende Kraft mathematischer Strukturen“, einem „Grundgedanken, den die exakte Naturwissenschaft unserer Zeit aus der Antike übernommen hat“; die Pythagoras zugeschriebene Entdeckung gehöre „zu den stärksten Impulsen menschlicher Wissenschaft überhaupt“.[36]
Noch in neuerer Zeit sind Darstellungen veröffentlicht worden, in denen die Legende ohne Hinweis auf ihre physikalische und historische Falschheit unkritisch wiedergegeben wird,[37] wie zum Beispiel im Sachbuch Der fünfte Hammer. Pythagoras und die Disharmonie der Welt von Daniel Heller-Roazen.[38]
Quellen[Bearbeiten | Quelltext bearbeiten]
- Gottfried Friedlein (Hrsg.): Anicii Manlii Torquati Severini Boetii de institutione arithmetica libri duo, de institutione musica libri quinque. Minerva, Frankfurt am Main 1966 (Nachdruck der Ausgabe Leipzig 1867, online; deutsche Übersetzung online)
- Michael Hermesdorff (Übersetzer): Micrologus Guidonis de disciplina artis musicae, d. i. Kurze Abhandlung Guidos über die Regeln der musikalischen Kunst. Trier 1876 (online)
- Ilde Illuminati, Fabio Bellissima (Hrsg.): Franchino Gaffurio: Theorica musice. Edizioni del Galluzzo, Firenze 2005, ISBN 88-8450-161-X, S. 66–71 (lateinischer Text und italienische Übersetzung)
Literatur[Bearbeiten | Quelltext bearbeiten]
- Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon (= Erlanger Beiträge zur Sprach- und Kunstwissenschaft. Band 10). Hans Carl, Nürnberg 1962
- Anja Heilmann: Boethius' Musiktheorie und das Quadrivium. Eine Einführung in den neuplatonischen Hintergrund von "De institutione musica". Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-25268-0, S. 203–222 (eingeschränkte Vorschau in der Google-Buchsuche)
- Werner Keil (Hrsg.): Basistexte Musikästhetik und Musiktheorie. Wilhelm Fink, Paderborn 2007, ISBN 978-3-8252-8359-9, S. 342–346 (eingeschränkte Vorschau in der Google-Buchsuche)
- Barbara Münxelhaus: Pythagoras musicus. Zur Rezeption der pythagoreischen Musiktheorie als quadrivialer Wissenschaft im lateinischen Mittelalter (= Orpheus-Schriftenreihe zu Grundfragen der Musik. Band 19). Verlag für systematische Musikwissenschaft, Bonn–Bad Godesberg 1976
- Jørgen Raasted: A neglected version of the anecdote about Pythagoras’s hammer experiment. In: Cahiers de l’Institut du Moyen-Âge grec et latin. Band 31a, 1979, S. 1–9
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Akademie Verlag, Berlin 1997, ISBN 3-05-003090-9
Weblinks[Bearbeiten | Quelltext bearbeiten]
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 193–196; vgl. Károly Simonyi: Kulturgeschichte der Physik. 3. Auflage. Frankfurt am Main 2001, S. 62.
- ↑ Nikomachos von Gerasa, Handbuch der Harmonielehre 6, übersetzt bei Anja Heilmann: Boethius' Musiktheorie und das Quadrivium, Göttingen 2007, S. 345–347, wörtlich zitiert bei Iamblichos von Chalkis, Über das pythagoreische Leben 115–121, übersetzt von Michael von Albrecht: Jamblich. Pythagoras: Legende – Lehre – Lebensgestaltung, Darmstadt 2002, S. 109–113.
- ↑ Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 353 und Anm. 28.
- ↑ Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 193–196; vgl. Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, S. 28 f.
- ↑ Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 362–364; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 196–199. Skepsis hinsichtlich akustischer Experimente des Archytas äußert Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 129–148; vgl. S. 473–475. Er weist darauf hin, dass sich Archytas hauptsächlich auf Angaben seiner Vorgänger und auf Alltagserfahrung beruft.
- ↑ Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 355.
- ↑ Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 355; Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, S. 38 f., 46.
- ↑ James W. McKinnon: Jubal vel Pythagoras, quis sit inventor musicae? In: The Musical Quarterly, Bd. 64, Nr. 1, 1978, S. 1–28; Paul E. Beichner: The Medieval Representative of Music, Jubal or Tubalcain? (= Texts and Studies in the History of Mediaeval Education 2), Notre Dame (Indiana) 1954; Francis Olivier Zimmermann: La forge et l’harmonie. De Pythagore à Tubalcain et Jubal. In: Zimmermann: Orphée: arts vivants, arts de parole et mélodie (online).
- ↑ Jørgen Raasted: A neglected version of the anecdote about Pythagoras’s hammer experiment. In: Cahiers de l’Institut du Moyen-Âge grec et latin 31a, 1979, S. 1–9, hier: 6 f.; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 192.
- ↑ Siehe Factus est repente, Wort-Melodie-Beziehungen in der Gregorianik; Der erste Gesang des Kirchenjahres.
- ↑ Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik. Band 1, 9. Auflage. Berlin 1974, Kapitel 83: Schallsender, Abschnitt Longitudinalschwingungen.
- ↑ Markus Bautsch: Über die pythagoreischen Wurzeln der gregorianischen Modi (online).
- ↑ Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik. Band 1, 9. Auflage. Berlin 1974, Kapitel 83: Schallsender, Abschnitt Saite.
- ↑ Xenokrates Fragment 9 H. Siehe dazu Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 57 und Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 193.
- ↑ Diese Passage von Nikomachos' Werk ist herausgegeben, ins Englische übersetzt und kommentiert von Carl A. Huffman: Philolaus of Croton, Cambridge 1993, S. 145–165.
- ↑ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, S. 52.
- ↑ Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 355.
- ↑ Macrobius, Commentarii in somnium Scipionis 2,1,8–13.
- ↑ Boethius, De institutione musica 1,10–11, übersetzt von Anja Heilmann: Boethius' Musiktheorie und das Quadrivium, Göttingen 2007, S. 342–345.
- ↑ Zum wissenschafts- und erkenntnistheoretischen Hintergrund siehe Anja Heilmann: Boethius' Musiktheorie und das Quadrivium, Göttingen 2007, S. 205–218.
- ↑ Cassiodor, Institutiones 2,5,1; vgl. Iamblichos, De vita Pythagorica 121.
- ↑ Isidor, Etymologiae 3,16,1.
- ↑ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, S. 15–17.
- ↑ Hans Martin Klinkenberg: Der Verfall des Quadriviums im frühen Mittelalter. In: Josef Koch (Hrsg.): Artes liberales. Von der antiken Bildung zur Wissenschaft des Mittelalters, Leiden 1976, S. 1–32, hier: 24 f.
- ↑ Carmina Cantabrigiensia, Lied 45 und Pythagoras-Sequenz (erste Hälfte des 11. Jahrhunderts); siehe Walther Kranz: Pythagoras in den Carmina Cantabrigiensia (online; PDF; 2,3 MB).
- ↑ Guido von Arezzo, Micrologus 20 (deutsche Übersetzung online).
- ↑ Aldersbacher Sammelhandschrift, Clm 2599, fol. 96 v.,, Bayerische Staatsbibliothek, München
- ↑ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, S. 16, 76; Frank Hentschel: Sinnlichkeit und Vernunft in der mittelalterlichen Musiktheorie, Stuttgart 2000, S. 148–150 (online).
- ↑ Walter Salmen: Musikleben im 16. Jahrhundert, Leipzig 1976; schwarzweiße Fotografie online.
- ↑ Werner Keil (Hrsg.): Basistexte Musikästhetik und Musiktheorie, Paderborn 2007, S. 56 (Übersetzung von Zarlinos Text).
- ↑ Vincenzo Galilei: Discorso intorno all’opere di messer Gioseffo Zarlino. Florenz 1589 (online; PDF; 347 kB).
- ↑ Daniel Meisner: Thesaurus philopoliticus, Frankfurt 1626, S. 327.
- ↑ Georg Muffat: Nova Cyclopeias Harmonica (1690).
- ↑ Rupert Ignaz Mayr: Pythagorische Schmids-Fuencklein (1692).
- ↑ Werner Keil (Hrsg.): Basistexte Musikästhetik und Musiktheorie, Paderborn 2007, S. 343.
- ↑ Werner Heisenberg: Gedanken der antiken Naturphilosophie in der modernen Physik. In: Werner Heisenberg: Wandlungen in den Grundlagen der Naturwissenschaft, 8. Auflage, Stuttgart 1949, S. 47–53, hier: 50.
- ↑ Arnold Keyserling: Geschichte der Denkstile. 3. Das logische Denken (online); Karl Sumereder: Musik und Mathematik (online); Arnold Keyserling: Der neue Name Gottes. Die Weltformel und ihre Analogien in der Wirklichkeit, Wien 2002, S. 71 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Daniel Heller-Roazen: Der fünfte Hammer. Pythagoras und die Disharmonie der Welt, Frankfurt am Main 2014, S. 14–22 (online).

































