Return on Investment
Return on Investment (deutsch „Rendite aus einer Investition“; Abkürzung: ROI; auch Kapitalrentabilität, Kapitalrendite, Kapitalverzinsung, Anlagenrentabilität, Anlagenrendite, Anlagenverzinsung) ist in der Betriebswirtschaftslehre der Anglizismus für eine betriebswirtschaftliche Kennzahl, die den aus einer unternehmerischen Tätigkeit (insbesondere einer Investition) resultierenden Erfolg – gemessen am eingesetzten Kapital – wiedergibt.
Allgemeines[Bearbeiten | Quelltext bearbeiten]
Der ROI ist ein Maß für die Ertragskraft eines Unternehmens und gibt an, welchen Gewinn das im Unternehmen investierte Kapital erbracht hat.[1] Die Kennzahl des ROI wird bei der (externen) Bilanzanalyse und im unternehmensinternen Controlling zur Messung der Rentabilität verwendet.[2]
Ermittlung[Bearbeiten | Quelltext bearbeiten]

Der ROI kann gemäß obiger Definition formal in folgender Gleichung dargestellt werden:
- .
Bei der Bilanzanalyse wird der in seiner weiten Fassung meist als Gesamtkapitalrentabilität definiert,[3] wobei der Jahresüberschuss dem Gesamtkapital gegenübergestellt wird:
- .
Die Kennzahl des ROI kann als durchschnittliche Verzinsung des im Unternehmen eingesetzten Kapitals interpretiert werden. Je nach Analyseziel kann der Jahresüberschuss etwa durch den Bilanzgewinn, durch das Betriebsergebnis oder durch den Gewinn vor Steuern bzw. den Gewinn nach Steuern ersetzt werden. Das Gesamtkapital setzt sich aus Eigenkapital und Fremdkapital, also der Bilanzsumme, zusammen. Durch die Einbeziehung des Fremdkapitals muss der Zinsaufwand für Fremdkapital () berücksichtigt werden, weil er den Jahresüberschuss geschmälert hat. Dann lautet die verfeinerte Formel:
- .
In der engeren Fassung wird dem Gesamtkapital lediglich das Betriebsergebnis gegenübergestellt.[4]

Eine weitere Verfeinerung ist die Kombination des Kapitalumschlags mit der Umsatzrentabilität,[5] wobei die Umsatzerlöse () zu berücksichtigen sind:
- .
Die nebenstehende Abbildung stellt Kapitalumschlag, Umsatzmarge sowie den resultierenden ROI für verschiedenen Technologieunternehmen im Jahre 2019 dar. Zur Orientierung ist ein WACC von 8 % (entspricht in etwa den durchschnittlichen Kapitalkosten der Unternehmen) abgetragen. Überdurchschnittlich hohe Umsatzrenditen deuten auf besondere Erfolge am Absatzmarkt. Unternehmen wie Apple oder Microsoft verfügen bei ihren Produkten über eine große Preissetzungsmacht und können gegenüber ihren Kunden hohe Margen durchsetzen. Die Margen sind bei Amazon.com im Handel deutlich geringer. Aufgrund des effizienten Kapitaleinsatzes bzw. des hohen Kapitalumschlags kann aber auch der Marktführer im Internethandel eine sehr hohe Kapitalrendite erwirtschaften.
Beim Cash Flow Return on Investment () wird der Brutto-Cashflow () dem Cash Value Added () gegenübergestellt:[6]
- .
Ziel des CFROI ist die Ermittlung der Rentabilität des operativen Geschäfts eines Unternehmens.[7] Ein Mehrwert wird geschaffen, wenn der CFROI höher ist als die durchschnittliche Kapitalverzinsung nach den Weighted Average Cost of Capital.
Der Return on Assets (ROA) ist ein Synonym für die Gesamtkapitalrentabilität und den ROI.[8] Die Eigenkapitalrendite (Return on Equity, ROE) ist eine weitere Variante des ROI. Der ROI bildet in der Regel die Spitzenkennzahl bei Kennzahlensystemen, da Unternehmen bzw. deren Investoren häufig eine Maximierung von Kapitalrenditen anstreben. So ist der ROI im Du-Pont-Schema als Multiplikation von Umsatzrentabilität und Kapitalumschlagshäufigkeit definiert. Durch Aufspaltung des ROI in verschiedene Bestandteile können Ansatzpunkte für die Erhöhung der Renditen aufgezeigt werden.
Die Anforderungen der Konsistenz von Kennzahlen verlangt, dass Zähler und Nenner in einer sachlich sinnvollen Beziehung zueinander stehen. Dies ist gewährleistet, wenn bei der Betrachtung einer Erfolgsgröße der dabei verwendete Kapitaleinsatz herangezogen wird. Darüber hinaus wird die erwirtschaftete Rendite (ROI) regelmäßig der geforderten Rendite der Kapitalgeber (Kapitalkosten) gegenübergestellt. Ein konsistenter Vergleich von Kapitalrenditen und Kapitalkosten sollte sich auf eine einheitliche Abgrenzung des betrachteten Kapitaleinsatzes sowie eine einheitliche Berücksichtigung von Steuern stützen.
ROI als Gesamtkapitalrendite (ROA)[Bearbeiten | Quelltext bearbeiten]
Traditionell wird der ROI auf Grundlage des in der Bilanz ausgewiesenen Gesamtkapitals berechnet. Das Gesamtkapital verteilt sich auf Eigentümer und Fremdkapitalgeber, demzufolge muss bei der Erfolgsgröße im Nenner des ROI ein Erfolg vor Zinsen abgebildet werden. Erfolgsgrößen vor Zinszahlungen beschreiben in einer Periode eine Vermögensmehrung für alle Kapitalgeber.
- Beispiel
Apple Inc. verfügte Ende 2019 über ein Gesamtkapital von 338,5 Mrd. US-Dollar (USD). Der Jahresüberschuss inklusive des gezahlten Zinsaufwands belief sich im Jahr 2019 auf 58,8 Mrd. USD. Daraus errechnet sich eine Gesamtkapitalrendite von 58,8/338,5 = 17,4 %.
- Würdigung
Die Gesamtkapitalrendite lässt sich einfach und schnell aus den (veröffentlichten) Unternehmensdaten eines Unternehmens berechnen. Die Aussagekraft der Gesamtkapitalrendite ist jedoch in vielen Fällen eingeschränkt:
- Nicht-betriebliche Bestandteile: Sowohl die Erfolge als auch die Kapitalgrößen enthalten nicht-betriebsnotwendige Bestandteile. Als nicht-betriebsnotwendiges Vermögen bezeichnet man Vermögenswerte, die jederzeit veräußert werden können, ohne die betriebliche Leistungserstellung zu beeinträchtigen und den Betriebszweck zu gefährden. Hierbei handelt es sich regelmäßig um nicht-betriebsnotwendige Finanzanlagen (kurzfristig, langfristig), nicht-betriebsnotwendige Kassenbestände und ggf. auch nicht-betriebsnotwendige Immobilien. Demzufolge handelt es sich bei der Gesamtkapitalrendite um eine Mischrendite auf das betriebliche und nicht-betriebliche Vermögen. Auf die Erfolge aus dem nicht-betriebsnotwendigen Vermögen hat das Management eines Unternehmens jedoch kaum Einfluss, sie werden vornehmlich von der Entwicklung auf den Finanz- oder Immobilienmärkten getrieben. Folglich eignet sich die Gesamtkapitalrendite weniger dazu, die Performance des Managements in einer Rechnungsperiode zu beurteilen. Der Vergleich der Gesamtkapitalrendite von verschiedenen Unternehmen wird beim Betriebsvergleich ebenfalls durch die nicht-betrieblichen Bestandteile verzerrt.
- Kapitaleinsatz zu Buchwerten: Die Bilanzansätze (Buchwerte) des Vermögens entsprechen kaum dem tatsächlich gebundenen Vermögen der Investoren. Die Rechnungslegung wurde für Unternehmen des Industriezeitalters entwickelt. Viele Unternehmen (insbesondere aus dem Dienstleistungssektor) verfügen jedoch auch über bedeutsames Vermögen in Form von Markennamen, Humankapital, selbst geschaffenes Software, Lizenzen, Kundenbindung etc. Dieses immaterielle Vermögen wird häufig aufgrund mangelnder Quantifizierung in den Bilanzen nicht oder nicht angemessen erfasst. Darüber hinaus wird das eingesetzte Vermögen gemäß Vorsichtsprinzips eher zu niedrig ausgewiesen. So betragen die Marktwerte der Unternehmen im Deutschen Aktienindex DAX in etwa das 3-fache ihrer Buchwerte. In der Folge überschätzt die Gesamtkapitalrendite regelmäßig die tatsächliche Rendite auf das aktuell zu Marktwerten gebundene Kapital der Investoren.
ROI als operative Kapitalrendite (Return-on-Capital-Employed, Return-on-Invested-Capital, Return-on-Net-Assets)[Bearbeiten | Quelltext bearbeiten]


Aufgrund der Schwächen der Gesamtkapitalrendite werden heute vorwiegend operative Kapitalrenditen berechnet. Dabei werden ebenfalls betriebliche Ergebnisse vor dem Zinsergebnis (englisch before interest) herangezogen. Zu beachten ist hierbei, dass sich hier das „before interest“ nicht nur auf die gezahlten Zinsen, sondern umfassender auf das gesamte Finanzergebnis bezieht. Es werden mithin auch Zinserträge oder das Beteiligungsergebnis ausgeblendet. Betriebliche Ergebnisse wie das EBIT oder das NOPAT offenbaren die Ertragskraft im originären Geschäft eines Unternehmens und sind Ausdruck der Fähigkeiten des Managements und der Positionierung des Unternehmens im Wettbewerb. Auf das Finanzergebnis (Zinsergebnis und Beteiligungsergebnis) hat das Management hingegen kaum Einfluss. Operative Ergebnisse werden von der Finanzierung des Unternehmens nicht beeinflusst oder − anders formuliert − sie sind unabhängig von der Kapitalstruktur des Unternehmens. Bei Betrachtung des EBIT im Zähler des ROI handelt es sich dann um eine Kapitalrendite vor Steuern bzw. bei Betrachtung des NOPAT um eine Kapitalrendite nach Steuern.
Kapitalrenditen vor Steuern (auf Basis des EBIT-Ergebnisses) eignen sich eher für die Beurteilung der Performance des Managements und sind international besser vergleichbar (Steuerquoten können sich erheblich unterscheiden). Kapitalrenditen nach Steuern zeigen dagegen realistischer die endgültige Rendite für die Investoren auf, da Steuern zweifellos abfließen und keine Werte schaffen. Kapitalrenditen nach Steuern (auf Basis des NOPAT-Ergebnisses) werden deshalb regelmäßig im Rahmen der wertorientierten Unternehmenssteuerung eingesetzt.
Die Identifikation der betrieblichen Ergebnisse fällt recht leicht, da die Gewinn- und Verlustrechnung (GuV) eine Spaltung der Ergebnisse in betriebliche (Betriebsergebnis) und nicht-betriebliche Bestandteile (Finanzergebnis) vorsieht. Hierbei ist zu beachten, dass die Rechnungslegung nicht auf eine Ermittlung des nachhaltigen Erfolgs ausgelegt ist. Einmaleffekte oder außergewöhnliche Effekte können die ausgewiesenen Erfolge überlagern und sollten ggf. bereinigt werden.
Aus analytischer Sicht ist es allerdings problematisch, dass die Aufspaltung des Vermögens in der Bilanz nicht mit der Aufspaltung des Erfolgs in der GuV korrespondiert. Die Gliederung der Bilanz ist eher den Bedürfnissen der Gläubiger ausgerichtet (Gläubigerschutz). Die Einteilung in kurz- und langfristiges Vermögen bzw. Schulden ermöglicht eine sinnvolle Analyse der Zahlungsfähigkeit/Liquidität eines Unternehmens. Die Gliederung nach Fristigkeit korrespondiert aber nicht mit der Darstellung in der GuV. In der Erfolgsrechnung wird der Erfolg nach den Quellen des Erfolgs (Leistungsbereich, Finanzbereich) aufgespalten. Für sinnvolle Gegenüberstellung von Erfolg und Kapitaleinsatz muss die Bilanz entsprechend umgestellt werden. Dies verdeutlicht nebenstehende Abbildung.
Bei Verwendung von operativen Erfolgsgrößen wie dem EBIT oder dem NOPAT muss ebenfalls bedacht werden, dass die operativen Erfolge auch Finanzierungskosten aus unverzinslichen Verbindlichkeiten (erhaltene Anzahlungen, Verbindlichkeiten aus Lieferungen und Leistungen) enthalten. Die Vorfinanzierungen von Lieferanten machen sich in entsprechend höheren Rechnungsbeträgen bzw. Materialaufwand bemerkbar und vermindern die ausgewiesenen operativen Erfolge des Unternehmens. Eine konsistente Ermittlung der Kapitalgröße verlangt, dass die unverzinslichen Verbindlichkeiten dann nicht mehr als Teil des Fremdkapitals betrachtet werden sollten. Mit den reduzierten operativen Erfolgen muss nur noch ein entsprechend reduziertes Fremdkapital bedient werden. In die Berechnung von Kapitalgrößen sollte deshalb nur noch das verzinsliche Fremdkapital einfließen.
Die Betrachtung der Kapitalgrößen anhand der Bilanz macht deutlich, dass man den Kapitaleinsatz auf zwei Arten berechnen kann: Anhand der Aktivseite (englisch Asset Approach) sowie anhand der Passivseite (englisch Financing Approach). Die beiden Varianten verdeutlichen ebenfalls die zwei unterschiedlichen Interpretationsmöglichkeiten für den ROI. Der auf Grundlage der Aktivseite berechnete ROI zeigt auf, wie sich das im Unternehmensprozess gebundene Kapital verzinst. Dieses im Betriebsprozess gebundene Kapital nach Abzug des unverzinslichen Fremdkapitals bezeichnet man auch als Net Assets bzw. die entsprechende Kapitalrendite als Return-on-Net-Assets (RONA).[9] Die Net-Assets eines Unternehmens entsprechen dem Anlagevermögen zuzüglich des Nettoumlaufvermögens (englisch Net Working Capital). Diese Sichtweise ist insbesondere zur Beurteilung der Leistungen des Managements relevant. Die Leistungen des Managements sollte sich daran messen, wie es das ursprünglich im Betriebsprozess eingesetzte Kapital verzinst.
Das auf Grundlage der Passivseite berechnete Kapitaleinsatz zeigt auf, wie sich das von den Kapitalgebern (Gesellschafter und Gläubiger) investierte Kapital rentiert. Diesen Kapitaleinsatz bezeichnet man auch als Capital Employed bzw. die entsprechende Kapitalrendite als Return on Capital Employed (ROCE).[10] Das Capital Employed eines Unternehmens setzt sich dann aus dem ausgewiesenen Eigenkapital und dem verzinslichen Fremdkapital zusammen. Der ROI ist deshalb auch ein Indikator dafür, wie sich das von den Investoren zur Verfügung gestellte Kapital verzinst. Sie wollen zumindest eine Rendite erzielen, welche ihre Kapitalkosten (WACC) abdeckt. Aufgrund der Wertgleichheit von Aktiv- und Passivseite der Bilanz entspricht der ROCE regelmäßig dem RONA.
Die Berechnungen von ROCE oder RONA basieren auf den Wertansätzen der Bilanz. Die Aussagekraft dieser Kennzahlen ist erheblich eingeschränkt, wenn es umfangreiches Vermögen oder umfangreiche Schulden gibt, die nicht in der Bilanz offengelegt werden. Hierzu gehört Vermögen in Form von stillen Reserven (insbesondere in Immobilien) als auch nicht oder unter Marktwert bilanziertes Vermögen wie Markenname, Humankapital, Kundenloyalität oder selbst geschaffene Software und Patente. Dieses immaterielle Vermögen wird regelmäßig in den Bilanzen nicht oder zu niedrig erfasst.[11] Derartige Bereinigungen bezeichnet man im angelsächsischen auch als „Shareholder Conversions“ bzw. als Ansatz von „Equity Equivalents“.
Auf der Passivseite der Bilanz werden häufig moderne Finanzierungsformen (wie operatives Leasing) nicht adäquat abgebildet. Der Barwert von Off-Balance-Finanzierungen ist allerdings nur dann zu berücksichtigen, falls auch die betrachteten Erfolge um die Zinserträge in den Leasingaufwendungen nach oben korrigiert wurden (dies ist eher selten der Fall). Den um nicht-bilanziertes Vermögen und Schulden bereinigten Kapitaleinsatz bezeichnet man auch als Invested Capital bzw. die Kapitalrendite auch als Return-on-Invested-Capital (ROIC). Aufgrund der vielfältigen Möglichkeiten zur Bereinigung findet man in der Praxis entsprechend viele Berechnungsschemata für den ROIC. Derartige Bereinigungen haben sich mittlerweile auch bei der Berechnung von ROCE oder RONA etabliert. Insofern werden die Bezeichnungen für die operativen Kapitalrenditen (ROCE, RONA, ROIC) häufig auch synonym verwendet.
- Beispiele

Für Apple berechnet sich auf Basis der Net Assets 2019 eine Kapitalrendite von 46,4 % vor Steuern bzw. 39,0 % nach Steuern. Die Rendite auf den Marktwert des gesamten Vermögens (inklusive Markenwerten, Kundenwerten etc.) belief sich dagegen nur auf 12,7 % vor Steuern bzw. 10,7 % nach Steuern. Die Abgrenzung des Kapitaleinsatzes bestimmt mithin maßgeblich die errechnete Rendite.
- Würdigung
Operative Kapitalrenditen sind der wichtigste Indikator dafür, wie profitabel das Kerngeschäft eines Unternehmens ist. Die Ertragskraft im originären Geschäft eines Unternehmens ist für alle Stakeholder des Unternehmens von besonderem Interesse. Bei der Berechnung der Erfolgs- und Kapitalgrößen ergeben sich jedoch viele Freiheitsgrade, welche die Aussagekraft und Vergleichbarkeit stark einschränken können.
Bei der Ermittlung einer geeigneten Kapitalrendite muss stets bedacht werden, zu welchem Zweck die Berechnung durchgeführt wird. Für die Beurteilung der Performance des Managements sollte die Kapitalgröße den Wert des ursprünglich im Unternehmensprozess eingesetzten Kapitals darstellen. Das Management muss sich daran messen lassen, wie effizient es das ursprünglich zur Verfügung gestellte Kapital verzinst. Der Ansatz von nicht betriebsnotwendigem Vermögen sollte demzufolge eher behutsam vorgenommen werden. Stille Reserven im Vermögen (z. B. aufgrund gestiegener Immobilienwerte) oder Markenwerte begründen sich häufig auf Eigenschaften des Marktes (z. B. Markteintrittsbarrieren), für die das Management nicht verantwortlich gemacht werden kann. Vor diesem Hintergrund lassen sich bei den Kapitalgrößen auch die Net Assets bzw. das Capital Employed rechtfertigen, da sie dem ursprünglich investierten Kapital recht nahe kommen.
Für die Investoren erscheint es dagegen sinnvoll, möglichst umfassend alle Vermögenswerte in der Kapitalgröße abzubilden. Investoren denken in Alternativen (Opportunitäten). Sie wollen erkennen, inwieweit sich ihr gesamtes im Betriebsprozess gebundene Vermögen im Vergleich zu alternativen Anlagen verzinst. Bei börsennotierten Unternehmen kann es deshalb auch sinnvoll sein, den Marktwert des betriebsnotwendigen Vermögens (Enterprise Value) als Kapitalgröße heranzuziehen.
ROI als Eigenkapitalrendite (ROE)[Bearbeiten | Quelltext bearbeiten]
Die Eigenkapitalrentabilität (kurz: EKR, auch: Eigenkapitalrendite) legt offen, wie sich das Eigenkapital eines Unternehmens innerhalb einer Rechnungsperiode verzinst. Ein Unternehmer oder Gesellschafter (Aktionär) soll anhand der Eigenkapitalrentabilität erkennen, ob sein investiertes Kapital im Unternehmen rentabel angelegt ist.
- Beispiel
Für Apple berechnet sich per Ende 2019 auf Basis eines Eigenkapitals von 89,5 Mrd. USD und eines Jahresüberschusses von 57,5 Mrd. USD eine Eigenkapitalrendite von 64,2 %.
- Würdigung
Die Eigenkapitalrendite lässt sich einfach und schnell aus den (veröffentlichten) Finanzkennzahlen eines Unternehmens berechnen. Auch die Aussagekraft der Eigenkapitalrendite ist in vielen Fällen eingeschränkt. Die Bilanzansätze (Buchwerte) des Eigenkapitals entsprechen kaum dem tatsächlich gebundenen Vermögen der Eigentümer. Immaterielles Vermögen wie Markennamen, Humankapital, selbst geschaffenes Software, Lizenzen, Kundenbindung etc. werden regelmäßig in den Bilanzen unterbewertet. Darüber hinaus wird das Reinvermögen (Eigenkapital) gemäß dem Vorsichtsprinzips eher zu niedrig ausgewiesen. Die Eigenkapitalrendite spiegelt deshalb kaum die tatsächliche Rendite auf das gebundene Kapital der Eigentümern dar. Für die Unternehmenssteuerung ist die Kennzahl ungeeignet, da das Management nicht nur über Eigenkapital, sondern auch über Fremdkapital verfügt, mit dem es im Betriebsprozess arbeiten muss. In der Praxis ist die Eigenkapitalrentabilität deshalb von untergeordneter Bedeutung.
Aufspaltung in Kennzahlensysteme[Bearbeiten | Quelltext bearbeiten]

Die Aufspaltung der Erfolge kann mit Hilfe von Kennzahlensystemen weiter vorangetrieben werden. Ein Kennzahlensystem bezeichnet eine Gesamtheit von Kennzahlen, die in einer sachlich sinnvollen Beziehung zueinander stehen. Mit Hilfe eines Kennzahlensystems können die Einflüsse auf die übergeordnete Kennzahl präziser herausgearbeitet werden. Die Spitzenkennzahl bei Kennzahlensystemen bildet regelmäßig der ROI, da die Kapitalgeber bzw. die Unternehmen eine Maximierung von Kapitalrenditen anstreben.
Die Entwicklung des ersten Kennzahlensystems geht bis ins Jahr 1919 zurück, als das amerikanische Chemieunternehmen Dupont das Du-Pont-Schema entwickelte. Ausgangspunkt ist die Aufspaltung des ROI in den Kennzahlen Umsatzrentabilität und Kapitalumschlag. Die weitere Untergliederung informiert über die Zusammensetzung der Erfolge bzw. des Kapitaleinsatzes. Dabei existieren heute zahlreiche Varianten des DuPont-Kennzahlensystems. Bei internationalen Konzernen dominieren heute Kennzahlensysteme auf Basis des Umsatzkostenverfahren. Bei der Rechnungslegung nach IFRS ist das Umsatzkostenverfahren gängige Praxis und nach den US-GAAP ist das Gesamtkostenverfahren sogar verboten.
- Würdigung
Kennzahlensysteme sind leicht verständlich und ermöglichen wertvolle Einblicke in die Zusammensetzung des übergeordneten Gesamterfolgs. Es lässt sich in der externen Analyse leicht umsetzen, da die benötigten Daten problemlos aus der GuV und der Bilanz entnommen werden können. Auf der anderen Seite ist ein Kennzahlensystem stets eine Vergangenheitsbetrachtung. Kennzahlen, die Basis für zukünftige Erfolge legen können (z. B. Erweiterungsinvestitionen oder Forschungs- und Entwicklungskosten) werden regelmäßig ausgeblendet. Das System orientiert sich eher an der Rechnungslegung und spaltet ausschließlich Aufwands- und Kapitalgrößen auf. Damit wird der Blick auf einen effizienten Umgang mit Ressourcen (Kosten, Kapitaleinsatz) gelenkt. Markteinflüsse und erfolgreiche Strategien am Absatzmarkt werden kaum beachtet. Dies wird auch dadurch deutlich, dass eine Aufspaltung in verschiedene Umsatzbestandteile unterbleibt. Für ein umfassendes Verständnis der Werttreiber ist es deshalb zwingend erforderlich, auch Marktanalysen, Produktanalysen und Analysen der Strategien des Unternehmens vorzunehmen.
Empirische Ergebnisse für Zeit-, Betriebs- und Branchenvergleiche[Bearbeiten | Quelltext bearbeiten]
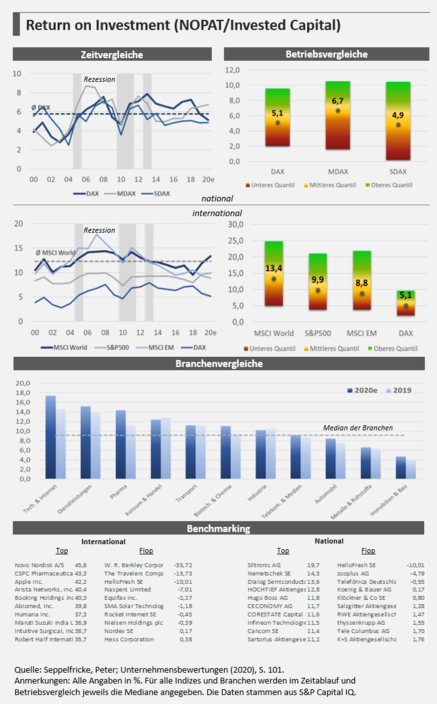
Die aktuellen Zeit-, Betriebs- und Branchenvergleiche für den ROI (NOPAT/Capital Employed) zeigt die nebenstehende Abbildung. Die empirische Analyse ermöglicht verschiedene Erkenntnisse:
- Positiver Trend: Die Kapitalrenditen konnten sowohl national als auch international in den vergangenen Jahren ausgebaut werden. Dies ist ein Indiz für eine nachlassende Wettbewerbsintensität aufgrund von Konzentrationsprozessen in verschiedenen Branchen. Oligopolistische oder gar monopolistische Strukturen erlauben eine größere Preissetzungsmacht der Anbieter und führen regelmäßig zu höheren Gewinnmargen. Der positive Trend ist auch dadurch begründet, dass in den vergangenen Jahren insbesondere Branchen gewachsen sind (Internet, Telekommunikation), die über vergleichsweise hohe Markteintrittsbarrieren verfügen.
- Abhängigkeit von der Größe: Großunternehmen im MSCI World können höhere Renditen erzielen als kleinere Unternehmen im DAX, MDAX oder SDAX. Dies ist ein Beleg für die Existenz von Economies-of-Scale-and-Scope sowie von Kapitalmarktanomalien. Interessant ist auch, dass die Kapitalrenditen von größeren Unternehmen in Krisen stabiler sind. Dies dürfte darauf zurückzuführen sein, dass größere Unternehmen häufig auch breiter diversifiziert sind.
- Abhängigkeit von der Branche: Es fällt auf, dass insbesondere Technologieunternehmen, Dienstleistungsunternehmen und Pharma-Unternehmen deutlich überdurchschnittliche Renditen erzielen können. Dies ist auf die erheblichen Markteintrittsbarrieren in diesen Sektoren zurückzuführen.
Return-on-Investment bei Einzelinvestitionen[Bearbeiten | Quelltext bearbeiten]
Diese moderne, erweiterte Auffassung des ROI unterscheidet sich zur ursprünglichen Variante nach DuPont hauptsächlich dadurch, dass nicht das Gesamtkapital eines Unternehmens betrachtet wird, sondern Einzelinvestitionen im Rahmen unternehmerischer Tätigkeit. Dabei sollten jedoch Berechnung (Ermittlung des reinen Zahlenwertes) und Analyse (systematische Untersuchung der Rückflüsse) unterschieden werden. Bei einer Berechnung des ROI bezogen auf eine Einzelinvestition wird grundsätzlich davon ausgegangen, dass die Rückflüsse der Investition aus einer vorangegangenen Analyse bereits bekannt sind:
Grundsätzlich ist eine Berechnung des ROI nur dann interessant, wenn die Investition auch zum Unternehmenserfolg beitragen kann, d. h., dass eine Amortisation innerhalb der Nutzungsdauer erreicht wird. Nun muss beispielsweise in der Informations- und Kommunikationsbranche der Umstand berücksichtigt werden, dass die Nutzungsdauer für Hard- und Softwareprodukte vergleichsweise niedrig ist, in der Regel für drei Jahre angesetzt wird. Somit gilt die Faustregel, dass nur Investitionen mit einer Amortisation von unter drei Jahren vorteilhaft sind. Wird eine Gewinnschwelle sogar innerhalb von 12 Monaten erreicht, so ist die Investition budgetneutral. Entsprechend diesen kurzfristigen Planungshorizonten ist es sinnvoll, den ROI auch im Vorfeld einer Investition berechnen zu können, was eine Berechnung für die gesamte Nutzungsdauer sinnvoll erscheinen lässt.
Unterschiede in der Berechnung[Bearbeiten | Quelltext bearbeiten]
Für die Methodik der Berechnung existieren somit zwei unterschiedliche Auffassungen. Diese erlauben jedoch eine unterschiedliche Interpretation des Ergebnisses bzw. sind zur Beurteilung bestimmter Investitionen unterschiedlich geeignet. Bei der Ermittlung des ROI für die gesamte Nutzungsdauer sind die prognostizierten Rückflüsse die alles entscheidende Größe.
Langfristige Berechnung unter Einbeziehung des Totalerfolgs[Bearbeiten | Quelltext bearbeiten]
Diese Methode ist besonders dann sinnvoll, wenn ein periodischer Bezug auf Grund der niedrig anzusetzenden Nutzungsdauer ungeeignet erscheint. Der ROI wird somit für einen länger veranschlagten Planungshorizont, beispielsweise für die gesamte Nutzungsdauer, berechnet. Dies geschieht meist im Vorfeld einer Investition und gilt als Entscheidungskriterium für ein mögliches Auswahlverfahren.
- .
Totalerfolg[Bearbeiten | Quelltext bearbeiten]
Um den Totalerfolg bzw. den Kapitalwert einer Investition zu einem bestimmten Zeitpunkt zu ermitteln, ist es zuerst einmal notwendig, die Rückflüsse der Investition zu prognostizieren. Diese entstehen beispielsweise durch höhere Erlöse und/oder Einsparungen, werden aber um den Betrag der Betriebskosten der Investition, insbesondere bei Sachanlagen, entsprechend geschmälert. Werden nun die Rückflüsse der Investition auf den Barwert/Gegenwartswert entsprechend diskontiert und per Saldo mit den Investitionskosten verrechnet, so entspricht dies dem Kapitalwert. Vereinfacht und bei entsprechend geringer Nutzungsdauer ist es auch möglich, auf die Diskontierung bzw. die Berücksichtigung eines internen Zinsfußes zu verzichten. Wird eine sehr schnelle Amortisation erwartet, beispielsweise 12 Monate, so kann auch die nächstliegende periodische Größe, in diesem Fall zwei Jahre, veranschlagt werden. Ist die Investition ein Erfolg, so müsste im Ergebnis ein positiver Kapitalwert erreicht werden. Ist der Kapitalwert Null, so hat sich die Investition exakt innerhalb des veranschlagten Zeitraums amortisiert.
Investitionskosten[Bearbeiten | Quelltext bearbeiten]
Die Investitionskosten sind das gesamte gebundene Kapital einer Investition. Hierbei sollten somit alle Kosten berücksichtigt werden, die einmalig und zeitnah zur Anschaffung anfallen. Folglich müssen auch Kosten, beispielsweise bei der Anschaffung einer Maschine, für die fachgerechte Installation in die Berechnung einbezogen werden. Andere Beispiele wären Schulungskosten im Rahmen der Einführung einer neuen Software oder auch Transportkosten.
Interpretation[Bearbeiten | Quelltext bearbeiten]
Der ROI drückt somit das Verhältnis aus dem erwarteten Mehrwert und den Kosten einer Investition aus. Sofern die Investitionskosten angegeben sind, wird eine Aussage über den betriebswirtschaftlich interessanten Totalerfolg zu einem bestimmten Zeitpunkt getroffen. Es handelt sich somit nicht mehr um eine periodisch zu ermittelnde Kennzahl. Im Ergebnis sollte immer ein positiver Prozentwert stehen, es sei denn, die Investition hat sich bis zum veranschlagten Zeitpunkt noch nicht amortisiert.
Periodische Ermittlung[Bearbeiten | Quelltext bearbeiten]
Diese Art der Berechnung ähnelt dem Prinzip nach Du-Pont am meisten und bietet sich vor allem bei einer langfristigen Investition an, wenn also keine kurzfristige Amortisation erwartet werden kann. Diese Form der Berechnung ist ebenso sinnvoll, wenn eine Planung der Rückflüsse im Vorfeld der Investition schwierig ist. Folglich dienen bereits erzielte Rückflüsse, beispielsweise aus der ersten Periode, zur Berechnung des ROI. Dabei gilt, je langfristiger dieser Zeitraum zu sein scheint, desto weniger sinnvoll ist es, mit den Rückflüssen der ersten Periode zu planen, ohne diese entsprechend auf den Gegenwartswert zu diskontieren. Ebenso wichtig ist die Berücksichtigung eines Lernkurveneffektes, der die Produktivität und somit die erzielten Rückflüsse der ersten Periode entsprechend schmälert, was eine weitere Planung schwieriger gestaltet. Die meisten Investitionen unterliegen jedoch nicht den Auswirkungen eines solchen Effektes.
- .
Interpretation[Bearbeiten | Quelltext bearbeiten]
Mit dem Ergebnis können Schlüsse bezüglich der Dauer der Amortisation gezogen werden. Es wird ausgedrückt, welcher Teil der Investition periodisch zurückkehrt. Man könnte somit auch von einer Annuität sprechen.
Wirtschaftliche Aspekte[Bearbeiten | Quelltext bearbeiten]
Ein besonderes Augenmerk gilt häufig der Analyse der operativen Ertragskraft eines Unternehmens. Dabei werden im Nenner des ROI Erfolgsgrößen vor Zinszahlungen (genauer vor Finanzergebnissen) analysiert. Operative Gewinne (wie z. B. EBIT oder NOPAT) oder operative Cashflows (wie z. B. EBITDA) werden nicht durch Erfolge im Finanzgeschäft (spiegeln sich in Finanzanlagen und Beteiligungen wider), von den Rahmenbedingungen am Kapitalmarkt (spiegeln sich im Zinsergebnis wider) oder der speziellen steuerlichen Situation des Unternehmens verzerrt. In der Folge eignen sich operative Kapitalrenditen sehr gut für Zeitvergleiche auf internationaler Ebene. Operative Kapitalrenditen eignen sich auch besser zur Beurteilung der Leistung des Managements, da viele Ergebnisbestandteile ausgeblendet werden, auf die das Management kaum Einfluss hat (Zinsergebnis, Beteiligungsergebnis, Steuern).
Der Zusammenhang zwischen Eigenkapitalquote, Verschuldungsgrad und ROI wird anhand des Leverage-Effekts deutlich. Bei gegebenem ROI steigt die Eigenkapitalquote als Folge des zunehmenden Verschuldungsgrads, solange der ROI über dem Fremdkapitalzins liegt.[12] Liegt dagegen der ROI unterhalb des Fremdkapitalzinses, befindet sich auch die Eigenkapitalrendite unterhalb der Gesamtkapitalrendite.
Der ROI kann nicht nur für Unternehmen, sondern für jede Art der Investition ermittelt werden. Das gilt für Investoren und auch für Anleger, bei denen der Kapitaleinsatz für das vorhandene Portfolio (Fondsvermögen, Wertpapierdepot) dem hieraus erwirtschafteten Kapitalertrag gegenübergestellt wird.[13] Bei einem einzelnen Finanzinstrument oder Finanzprodukt entspricht der ROI beispielsweise der Aktienrendite und der Anleiherendite.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Adolf G. Coenenberg et al.: Kostenrechnung und Kostenanalyse. 6. Auflage. Schäffer-Pöschel, Stuttgart 2007.
- Johann Steger: Kennzahlen und Kennzahlensysteme. 3. Auflage. NWB Verlag, Herne 2017.
- Helmut Schmalen, Hans Pechtel: Grundlagen und Probleme der Betriebswirtschaft. 13. Auflage. Schäffer-Pöschel, Stuttgart 2006.
- Peter Seppelfricke: Unternehmensanalysen: Wie man die Zukunft eines Unternehmens prognostiziert. Schäffer-Pöschel, Stuttgart 2019.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Artur Woll (Hrsg.): Wirtschaftslexikon. 2008, S. 667 f. (google.de)
- ↑ Helmut Uhlir: Return on Investment. In: Wolfgang Lück (Hrsg.): Lexikon der Betriebswirtschaft. 1983, ISBN 3-478-37620-3, S. 1003.
- ↑ Siegfried G. Häberle (Hrsg.): Das neue Lexikon der Betriebswirtschaftslehre. 2008, S. 484. (google.de)
- ↑ Hans-Ulrich Krause: Controlling-Kennzahlen für ein nachhaltiges Management. 2016, S. 63 f. (google.de)
- ↑ Wolfgang Becker, Stefan Lutz, Christian Back: Gabler Kompaktlexikon Modernes Rechnungswesen. 2011, S. 207. (google.de)
- ↑ Springer Fachmedien Wiesbaden (Hrsg.): Kompakt-Lexikon Internationale Wirtschaft. 2013, S. 76. (google.de)
- ↑ Siegfried G. Häberle (Hrsg.): Das neue Lexikon der Betriebswirtschaftslehre. 2008, S. 186.
- ↑ Siegfried G. Häberle (Hrsg.): Das neue Lexikon der Betriebswirtschaftslehre. 2008, S. 484.
- ↑ Knut Bleicher: Das Konzept Integriertes Management. 2011, S. 130. (google.de)
- ↑ Nicolas Schmidlin: Unternehmensbewertung & Kennzahlenanalyse. 2020, S. 55. (google.de)
- ↑ Ausnahme: Gezahlte Kaufpreise bei Unternehmenskauf und Kaufpreisallokation des Vermögens gemäß IFRS 3
- ↑ Peter Seppelfricke: Handbuch Aktien- und Unternehmensbewertung. 2012, S. 220 f. (google.de)
- ↑ George T. Friedlob, Franklin J. Plewa, Jr.: Understanding Return on Investment. 1996, S. 11 f. (google.de)















