Kontinuumsmechanik
Kontinuumsmechanik ist ein Teilgebiet der Mechanik, das die Bewegung von deformierbaren Körpern als Antwort auf äußere Belastungen studiert. Der Begriff Deformation wird hier so weit gefasst, dass auch das Fließen einer Flüssigkeit oder das Strömen eines Gases darunter fällt. Entsprechend gehören Festkörpermechanik, Strömungsmechanik und Gastheorie zur Kontinuumsmechanik. In der Kontinuumsmechanik wird vom mikroskopischen Aufbau der Materie, also zum Beispiel der Gitterstruktur kristalliner Festkörper und der molekularen Struktur von Flüssigkeiten, abgesehen und der Untersuchungsgegenstand als ein Kontinuum genähert. Die Größen Dichte, Temperatur und die drei Komponenten der Geschwindigkeit liegen an jedem Raumpunkt innerhalb eines Körpers vor, was die Kontinuumsmechanik zu einer Feldtheorie macht.
Der theoretische Hintergrund der Kontinuumsmechanik liegt in der Physik, die praktische Anwendung erfolgt in verschiedenen Bereichen des Maschinenbaus, des theoretischen Bauingenieurwesens, der Werkstoffkunde, der Medizinischen Informatik sowie in der Geophysik und anderen Bereichen der Geowissenschaften. Insbesondere Anwendungen der beiden erstgenannten Bereiche werden als Technische Mechanik zusammengefasst.
Das im Bereich wissenschaftlich technischer Aufgabenstellungen der Festkörpermechanik bekannteste und am meisten angewandte numerische Berechnungsverfahren, die Finite-Elemente-Methode, löst die Gleichungen der Kontinuumsmechanik (näherungsweise) mit Methoden der Variationsrechnung. In der Strömungsmechanik kommt ein gleicher Rang dem Finite-Volumen-Verfahren zu.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Die Kontinuumsmechanik basiert auf der Mechanik, Physik, Differentialgeometrie, Differential- und Integralrechnung deren historischer Werdegang dort nachgeschlagen werden kann. Auch manche Etappen in der Entwicklung der Strömungsmechanik verlaufen mit der der Kontinuumsmechanik parallel. An dieser Stelle soll die spezifisch kontinuumsmechanische Entwicklung mit Betonung auf der Mechanik fester Körper skizziert werden.
Bereits Archimedes (287–212 v. Chr.) befasste sich mit grundlegenden mechanischen Fragestellungen, die Festkörper und Fluide betrafen, über 1500 Jahre bevor Leonardo da Vinci (1452–1519) Lösungen zahlreicher mechanischer Probleme ersann.
Galileo Galilei (1564–1642) diskutierte in seinen Discorsi Festigkeitsprobleme und begründete so die Festigkeitslehre in einer Zeit, als feste Körper zumeist als undeformierbar modelliert wurden. Edme Mariotte (1620–1684) lieferte Beiträge zu Problemen der Flüssigkeiten und Gase und stellte dabei erste Konstitutivgesetze auf, was Robert Hooke (1635–1703) mit dem nach ihm benannten Hooke’schen Gesetz 1676 auch für elastische Festkörper tat.
Isaac Newton (1643–1727) veröffentlichte 1686 seine Principia mit den Gravitations- und Bewegungsgesetzen. Die Mitglieder der Familie Bernoulli lieferten Beiträge zur Mathematik, Strömungsmechanik und – durch Jakob I Bernoulli (1654–1705) – zur Balkentheorie. Leonhard Euler (1707–1783) gab wesentliche Impulse zur Mechanik starrer und deformierbarer Körper sowie zur Hydromechanik. Jean-Baptiste le Rond d’Alembert (1717–1783) führte die eulersche Betrachtungsweise ein, leitete die lokale Massenbilanz her und formulierte das d’Alembertsche Prinzip. Joseph-Louis Lagrange (1736–1813) richtete 1788 in seinem grundlegenden Werk Mécanique analytique die Mechanik konsequent mathematisch aus.
Die in der Kontinuumsmechanik fundamentalen Begriffe des Spannungs- und Verzerrungstensors wurden von Augustin-Louis Cauchy (1789–1857) eingeführt. Weitere grundlegende Erkenntnisse wurden unter anderem von Siméon Denis Poisson (1781–1840), Claude Louis Marie Henri Navier (1785–1836), Gabrio Piola (1794–1850) und Gustav Robert Kirchhoff (1824–1887) eingebracht.
Aus industriellen und praktischen Bedürfnissen heraus dominierten im weiteren Verlauf technische Fragestellungen die Wissenschaft, die in Frankreich unter anderem in der von Cauchy, Poisson und Navier geprägten École polytechnique betrieben wurde. Deren Modell breitete sich in ganz Europa aus, in Deutschland als Technische Hochschule. Ingenieursdisziplinen wie Plastizitätstheorie, Kriechtheorie, Festigkeitslehre, Elastizitätstheorie und das Bauingenieurwesen entstanden. Als Folge dieser Aufsplitterung entwickelten sich Forschung und Lehre in den Teilgebieten unabhängig voneinander und gingen die kontinuumsmechanischen Zusammenhänge verloren. Auch die Strömungsmechanik entwickelte sich eigenständig.
Einen neuen Denkimpuls gab David Hilbert (1862–1943) mit seiner 1900 aufgestellten Liste von 23 mathematischen Problemen, die einer Lösung harren. Das sechste Problem „Wie kann die Physik axiomatisiert werden?“ ist zwar noch Anfang des 21. Jahrhunderts ungelöst, aber es entstanden noch vor dem Zweiten Weltkrieg fachübergreifende Arbeiten zur Kontinuumsmechanik insbesondere von Georg Hamel (1877–1954). Nach dem Krieg setzte eine intensive interdisziplinäre Grundlagenforschung ein, in der Clifford Truesdell (1919–2000) und Walter Noll (1925–2017) Impulse setzten.
Ab Mitte des 20. Jahrhunderts entwickelten sich die Computerhardware, Software und die Numerische Mathematik zur Lösung von Gleichungen so weit, dass mit ihrer Hilfe Antworten für komplexe, praktische, kontinuumsmechanische Probleme gefunden werden können.[1][2]
Überblick[Bearbeiten | Quelltext bearbeiten]
Die Kontinuumsmechanik enthält zwei unterschiedliche Kategorien von Aussagen:
- allgemeine Aussagen, die für alle materiellen Körper gelten, und
- individuelle Aussagen, die Materialeigenschaften modellieren.
Die allgemeinen Aussagen beschreiben die Kinematik, hier die Geometrie der Deformation eines Körpers, und die Naturgesetze, die das physikalische Verhalten der Materie bestimmen.
Die individuellen Aussagen über die Materialeigenschaften werden in der #Materialtheorie getroffen und schaffen die Verbindung zwischen den Naturgesetzen und den Deformationen von Körpern.
Die mathematische Beschreibung erlaubt die kompakte Formulierung der Naturgesetze in Bilanzgleichungen und der Materialeigenschaften in konstitutiven Gleichungen. Das System aus
- kinematischen Gleichungen,
- Bilanzgleichungen und
- konstitutiven Gleichungen
ist abgeschlossen und führt zur prinzipiellen Vorhersagbarkeit der Reaktion von Körpern auf äußere Einwirkungen.
Kinematik[Bearbeiten | Quelltext bearbeiten]
In der Kontinuumsmechanik ist es die Aufgabe der Kinematik, ein Maß für die Verzerrungen eines Körpers in Abhängigkeit von seiner Bewegung – inklusive Deformationen – zu definieren. Die Bewegung kann dabei von einem festen Raumpunkt oder von einem Partikel des Körpers aus beobachtet werden. Ersteres ist die Eulersche Betrachtungsweise, die die Strömungsmechanik benutzt, und letzteres die Lagrangesche Betrachtungsweise, die in der Festkörpermechanik bevorzugt wird.
Nun ist plausibel, dass wenn sich zwei im undeformierten Ausgangszustand benachbarte Partikel eines Körpers stark unterschiedlich bewegen, der Körper dort auch stark deformiert wird. Werden nun die in drei Raumrichtungen messenden Positionsdifferenzen der Partikel im deformierten Körper in Beziehung gesetzt zu ihren drei Positionsdifferenzen im undeformierten Ausgangszustand, entsteht bei kleiner werdenden Abständen der Partikel der Deformationsgradient, der ein lokales Maß für die Deformation des Körpers ist. Der Deformationsgradient kann in eine Drehung und rotationsfreie Streckung zerlegt werden, aus der sich die gesuchten Verzerrungsmaße ableiten.

Der Deformationsgradient F ist ein Tensor zweiter Stufe. Diese Tensoren dienen hier der linearen Abbildung von geometrischen Vektoren, die dabei im Allgemeinen gedreht und gestreckt werden. Der Deformationsgradient bildet speziell die Tangentenvektoren an materielle Linien, die man sich in den Körper eingeritzt vorstellen kann, von der unverformten Ausgangslage in die verformte momentane ab, siehe Abbildung rechts. Die Tensorrechnung kann nicht als allgemein bekannt vorausgesetzt werden, weshalb jedes Lehrbuch der Kontinuumsmechanik auch eine Einführung in die Tensorrechnung beinhaltet.
Naturgesetze[Bearbeiten | Quelltext bearbeiten]
Bei der Übertragung des materiellen Körpers in einen mathematischen Raum wird der Körper homogenisiert, indem die auf Atome verteilte Materie durch ein Kontinuum ersetzt wird, was namensgebend für diese Wissenschaft ist. Durch diese Idealisierung erhält jeder Punkt des Körpers physikalische Eigenschaften wie Geschwindigkeit, Dichte und Temperatur.

Das zweite Newton’sche Gesetz beschreibt die Reaktion eines Körpers auf eine äußere Kraft. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, die sich im Körper als Spannungen (mit der Dimension Kraft pro Fläche) fortpflanzen. Nun kann der Körper gedanklich zerschnitten werden, so dass sich an den Schnittflächen Schnittspannungen ausbilden, die jedoch von der Orientierung der Schnittflächen, d. h. ihren Normalenvektoren, abhängen, siehe Bild. Nach dem Cauchy’schen Fundamentaltheorem stellen Spannungstensoren diese Abhängigkeit dar, indem sie die Normalen der Schnittflächen linear auf die Schnittspannungen abbilden. Der Spannungstensor ist grundlegend für die Formulierung der Naturgesetze in ihrer am materiellen Punkt gültigen Form.
Die Bilanzgleichungen der Mechanik beschreiben die Wirkung der Außenwelt auf einen Körper und die daraus resultierende Änderung physikalischer Größen. Diese Größen sind die Masse, der Impuls, der Drehimpuls und die Energie. Der zweite Hauptsatz der Thermodynamik wird in Form der Clausius-Duhem-Ungleichung berücksichtigt. Die in der Mechanik für ausgedehnte Körper formulierten Naturgesetze werden in der Kontinuumsmechanik als globale Integralgleichungen ausgedrückt, aus denen sich mit geeigneten Annahmen lokale Differentialgleichungen ableiten lassen, die an jedem Raumpunkt oder Partikel erfüllt sein müssen.
- Die lokale #Massenbilanz besagt, dass die Dichte am materiellen Punkt zeitlich konstant ist.
- Die lokale #Impulsbilanz setzt die spezifische Impulsänderung in Beziehung zur spezifischen Schwerkraft und zum Antrieb durch einen Spannungsanstieg.
- Die #Drehimpulsbilanz reduziert sich auf die Forderung nach der Symmetrie des Spannungstensors.
- Die #Energiebilanz besagt, dass sich die innere Energie durch innere Wärmequellen, den spezifischen Wärmeeintrag und der spezifischen Spannungsleistung an Verzerrungsgeschwindigkeiten ändert.
- Bei isothermen Prozessen fordert die #Clausius-Duhem-Ungleichung schließlich, dass die Produktion an Helmholtz’scher freier Energie die spezifische Spannungsleistung nicht überschreiten darf.
Letztere Bedingung ist weniger als Einschränkung physikalischer Prozesse, sondern vielmehr als Anforderung an Materialmodelle zu interpretieren: Es muss sichergestellt sein, dass die lokalen Formen der Clausius-Duhem-Ungleichung von den konstitutiven Gleichungen für beliebige Prozesse erfüllt werden.
Materialtheorie[Bearbeiten | Quelltext bearbeiten]
Die mathematische Formulierung der Naturgesetze trifft keine Aussagen über die individuellen Eigenschaften der Körper – ob sie beispielsweise fest, flüssig oder gasförmig sind – und reicht daher nicht aus, die Bewegungen der Körper eindeutig zu bestimmen. Dazu bedarf es noch konstitutiver Gleichungen, die die materialspezifische Antwort des Körpers, z. B. auf eine äußere Kraft, beschreiben. In diesem Fall ist eine Beziehung zwischen den Deformationen des Körpers und den Reaktionskräften anzugeben. Die Materialtheorie beschäftigt sich mit diesen Beziehungen und wie sie in ein Materialmodell umgesetzt werden. Ziel eines Materialmodells ist es die wesentlichen Aspekte des Materialverhaltens zu beschreiben, wobei das was wesentlich ist, vom Beobachter festgelegt wird. Stoff- oder Materialgesetze, wie Materialmodelle manchmal genannt werden, haben nicht die allgemeine Gültigkeit physikalischer Gesetze.
Die klassische Kontinuumsmechanik betrachtet einfache Materialien, bei denen aus ihrer bisherigen Bewegung (Determinismus) das Verhalten an einem materiellen Punkt vollständig aus seiner Umgebung (Lokalität) bestimmt ist, und das unabhängig vom Bewegungszustand des Beobachters (Objektivität). Einfache Materialien sind also deterministisch, lokal und objektiv. Ihre Eigenschaften lassen sich mit materiellen Zwangsbedingungen, materiellen Symmetrien und konstitutiven Gleichungen wiedergegeben:
- Materielle Zwangsbedingungen schränken die Deformationsmöglichkeiten eines Materials ein, wie es z. B. die Inkompressibilität tut.
- Materielle Symmetrien beschreiben die Richtungsabhängigkeit des Materials, wie sie z. B. bei Holz gegeben ist.
- Die konstitutiven Gleichungen stellen schließlich eine Relation zwischen den Dehnungen und den Spannungen her.
Die sechs Materialmodelle der klassischen Materialtheorie sind das ideale Gas, das Newton’sche Fluid, das Hooke’sche Gesetz, die Viskoelastizität, Plastizität und Viskoplastizität. Aus den ersten drei Modellen leiten sich die Euler-Gleichungen, die Navier-Stokes-Gleichungen bzw. die Navier-Cauchy-Gleichungen ab.
Tensorrechnung[Bearbeiten | Quelltext bearbeiten]

Wichtigstes mathematisches Hilfsmittel der Kontinuumsmechanik ist die Tensorrechnung, deren Kenntnis nicht allgemein vorausgesetzt werden kann. Hier sollen nur die im vorliegenden Artikel benutzten Rechenregeln kurz vorgestellt werden.
Die in der Kontinuumsmechanik meist benutzten Tensoren sind Tensoren zweiter Stufe, die geometrische Vektoren aus dem dreidimensionalen euklidischen Vektorraum linear aufeinander abbilden. Dabei werden die Vektoren im Allgemeinen gedreht und gestreckt, siehe Abbildung rechts. Für diese Tensoren gilt die komponentenweise Darstellung
mit Koeffizienten des Tensors, die zu mit dem dyadischen Produkt „“ verknüpften Vektoren aus zwei Vektorraumbasen bzw. des angenommenen Vektorraums gehören. Von verschiedenen Basen wird bei der Beschreibung mit konvektiven Koordinaten Gebrauch gemacht. Hier genügt es die Basen und mit der Standardbasis zu identifizieren, so dass jeder Tensor mit seiner Matrixrepräsentation gleichgesetzt werden kann:
Gegeben sei ein weiterer Tensor und ein Vektor für die die komponentenweisen Darstellungen
gelten. Die im Artikel verwendeten Operationen sind wie folgt definiert:
| Operator | Definition |
|---|---|
| Addition und Subtraktion | |
| Multiplikation mit einem Skalar x | |
| Tensorprodukt | |
| Transposition | |
| Transformation eines Vektors mit dem Skalarprodukt „“ von Vektoren | |
| Invertierung | |
| Frobenius-Skalarprodukt |
Darin ist der Einheitstensor.
Des Weiteren wird die Fréchet-Ableitung benötigt, die die Differentialrechnung auf Vektoren und Tensoren verallgemeinert. Die Fréchet-Ableitung einer Funktion nach ist der beschränkte lineare Operator , der – sofern er existiert – in allen Richtungen dem Gâteaux-Differential entspricht, also
gilt. Darin ist und skalar-, vektor- oder tensorwertig aber und gleichartig. Dann wird auch
geschrieben. Für die Ableitungen nach den Koordinaten werden hier der Gradient und die Divergenz gebraucht.
| Feldvariable | Divergenz div | Gradient grad |
|---|---|---|
| Skalarfeld | ||
| Vektorfeld | ||
| Tensorfeld |
Darin ist 𝜵 der Nabla-Operator. Weitere Definitionen und Rechenregeln sind in der Formelsammlung Tensoralgebra und Formelsammlung Tensoranalysis aufgeführt.
Kinematik[Bearbeiten | Quelltext bearbeiten]
Hier sollen nur die spezifisch kontinuumsmechanischen Aspekte beschrieben werden, mehr ist im Hauptartikel nachzuschlagen. Die Kinematik gibt in der Kontinuumsmechanik Transformationsgleichungen für Größen in der Ausgangskonfiguration in die entsprechenden Größen in der Momentankonfiguration und leitet daraus Verzerrungsmaße ab.
Der materielle Körper[Bearbeiten | Quelltext bearbeiten]
Der materielle Körper als Träger der physikalischen Prozesse erfüllt gleichmäßig Teile des Raumes unserer Anschauung. In der Kontinuumsmechanik wird der Körper mittels Konfigurationen bijektiv in einen euklidischen Vektorraum abgebildet, wobei die Eigenschaften des Körpers kontinuierlich über den Raum verschmiert werden. Mithilfe dieser Idealisierung wird der Körper als Punkt-Menge beschrieben, in der Gradienten und Integrale gebildet werden können.
Daraus ergeben sich zwei Konsequenzen:
- Es gibt eine Größenskala, unterhalb derer die Aussagen der Kontinuumsmechanik ihre Gültigkeit verlieren. Diese Größenskala liegt oberhalb der Abmessungen des Repräsentativen-Volumen-Elementes (RVE), aus identischen Kopien von welchem der materielle Körper aufgebaut gedacht wird. Das RVE eines Kristalls kann beispielsweise eine Elementarzelle sein.
- Ein innerer Punkt des Körpers bleibt immer ein innerer Punkt, weswegen die Beschreibung der Ausbreitung von Rissen mit Aussagen der klassischen Kontinuumsmechanik nicht möglich ist. Mit der Reaktion von Körpern auf Risse und der Rissausbreitung beschäftigt sich die Bruchmechanik, die ihrerseits auf das Vorhandensein eines Risses angewiesen ist.
Für einen Körper werden folgende Konfigurationen benutzt:
- Die Referenz- oder Bezugskonfiguration , die der Identifikation der materiellen Punkte dient. Die Ausgangskonfiguration des Körpers zu einem gesetzten Zeitpunkt ist zeitlich fixiert und kann und soll als Referenzkonfiguration dienen. Weil diese Position einmal vom Körper eingenommen wurde, liefert diese Referenzkonfiguration ein Objekt unserer Anschauung.
- Die Momentankonfiguration bildet den deformierten Körper zur Zeit ab.
Die Verknüpfung dieser Konfigurationen
heißt Bewegungsfunktion und soll so oft stetig differenzierbar sein, wie es im jeweiligen Kontext notwendig ist.[3]:35
Materielle und räumliche Koordinaten[Bearbeiten | Quelltext bearbeiten]
Die materiellen Koordinaten eines materiellen Punktes sind die Koeffizienten seines Ortsvektors in der Ausgangskonfiguration:
Die Momentankonfiguration gibt zu jedem Zeitpunkt die räumlichen Koordinaten des materiellen Punktes im Raum:
Die Bewegungsfunktion beschreibt bei festgehaltenem die Bahnlinie eines materiellen Punktes durch den Raum. Wegen der Bijektivität kann die Bewegungsfunktion jederzeit invertiert werden:
Bei festgehaltenem Raumpunkt liefert die Bewegungsfunktion die Streichlinie durch den Raumpunkt.
Wegen der Eineindeutigkeit der Konfigurationen bei der Beschreibung des materiellen Körpers können alle einem materiellen Punkt zugeordneten Größen (z. B. Dichte, Temperatur und Geschwindigkeit) in Abhängigkeit von seinen materiellen oder räumlichen Koordinaten beschrieben werden.
Lagrange’sche Betrachtungsweise[Bearbeiten | Quelltext bearbeiten]
Soll die Bewegung eines materiellen Punktes beobachtet werden und welche physikalischen Bedingungen in ihm herrschen, liegt es nahe, die dem materiellen Punkt zugeordneten Größen in Abhängigkeit von den materiellen Koordinaten aufzuschreiben, denn diese sind für jeden materiellen Punkt konstant. So ergibt sich die materielle oder Lagrange’sche Betrachtungsweise (nach Joseph-Louis Lagrange), die in der Festkörpermechanik bevorzugt wird.
Euler’sche Betrachtungsweise[Bearbeiten | Quelltext bearbeiten]
Sollen andererseits die physikalischen Prozesse an einem festen Raumpunkt verfolgt werden, liegt es nahe, die physikalischen Größen in Abhängigkeit von den räumlichen Koordinaten zu notieren. Das ist die räumliche oder Euler’sche Betrachtungsweise, die in der Strömungsmechanik benutzt wird.
Schreibweisen[Bearbeiten | Quelltext bearbeiten]
Wenn nicht anders angegeben, werden Größen in der Lagrange’schen Betrachtungsweise mit Großbuchstaben oder dem Index und solche der Euler’schen mit Kleinbuchstaben bezeichnet. Das gilt auch für die #Differentialoperatoren: Die materiellen Operatoren DIV, GRAD und der Nabla-Operator 𝜵0 beinhalten die materiellen Ableitungen nach den materiellen Koordinaten . Die räumlichen Operatoren div, grad sowie 𝜵 in der räumlichen Formulierung bilden die räumlichen Ableitungen nach den räumlichen Koordinaten .
Lokale und materielle Zeitableitung[Bearbeiten | Quelltext bearbeiten]
Die Zeitableitung einer einem materiellen Punkt zugeordneten Größe, z. B. der Temperatur , kann bei festgehaltenem Raumpunkt oder festgehaltenem materiellen Punkt ausgewertet werden. Ersteres ist die lokale Zeitableitung letzteres die materielle oder substantielle Ableitung. Weil sich die Naturgesetze in der Mechanik auf materielle Punkte beziehen, ist die substantielle Zeitableitung hier physikalisch bestimmend.
Die substantielle Zeitableitung ist in der Lagrange’schen Betrachtungsweise die partielle Ableitung nach der Zeit
und wird hier auch mit dem aufgesetzten Punkt gekennzeichnet. In der Euler’schen Darstellung bildet sich die materielle Zeitableitung mit dem Nabla-Operator 𝜵 und :
Der zweite Term resultiert daraus, dass das Partikel in einen wärmeren oder kälteren Bereich eintritt (Konvektion). Analog bildet sich die materielle Zeitableitung einer vektoriellen Größe, beispielsweise die substantielle Beschleunigung:
Erstere Schreibweise mit dem Nabla-Operator wird in der Strömungsmechanik bevorzugt.
Der Deformationsgradient[Bearbeiten | Quelltext bearbeiten]

Der Deformationsgradient ist die grundlegende Größe zur Beschreibung von Verformungen, die sich aus lokalen Längenänderungen von materiellen Linienelementen und Winkeländerungen zwischen ihnen ergeben, die man sich als in das Material eingeritzt vorstellen kann. Der Deformationsgradient transformiert die Tangentialvektoren an materielle Linien in der Ausgangskonfiguration in die Momentankonfiguration, siehe Bild. Berechnet wird der Deformationsgradient aus der Ableitung der Bewegungsfunktion nach den materiellen Koordinaten
und kann auch mit der Richtungsableitung
dargestellt werden, was seine Transformationseigenschaften der Linienelemente verdeutlicht.
Der Deformationsgradient transformiert auch das Oberflächenelement , der mit dem Flächenstück multiplizierten Normalen des Flächenstücks, und das Volumenelement von der Ausgangskonfiguration in die Momentankonfiguration:
Der Operator gibt die Determinante und die transponiert Inverse. Mit diesen Elementen können Integrale in der Ausgangs- und der Momentankonfiguration (gleichbedeutend: in der materiellen und räumlichen Darstellung) ineinander umgerechnet werden.
Verzerrungstensoren[Bearbeiten | Quelltext bearbeiten]
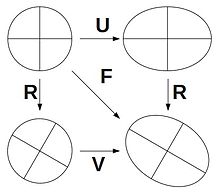
Mithilfe des Deformationsgradienten werden die Verzerrungsmaße definiert. Die Polarzerlegung des Deformationsgradienten spaltet die Verformung lokal in eine reine Drehung, vermittelt durch den orthogonalen Rotationstensor , und eine reine Streckung, vermittelt durch die symmetrischen positiv definiten rechten bzw. linken Strecktensor bzw. , siehe Bild. Der räumliche Tensor wird hier groß geschrieben, um eine Verwechselung mit der Geschwindigkeit zu vermeiden, die gelegentlich auch mit fetten Buchstaben geschrieben wird.
Die Strecktensoren dienen der Definition einer Vielzahl von Verzerrungstensoren, z. B. der Biot-Dehnungen der Hencky Dehnungen (berechnet mittels Hauptachsentransformation von , Bildung der Logarithmen der Diagonalelemente und Rücktransformation), der Green-Lagrange’schen Dehnungen
und Euler-Almansi-Dehnungen
Wie oben steht für den Einheitstensor. Die letzten beiden Dehnungstensoren sind aus dem Vergleich zweier materieller Linienelemente und im Punkt motiviert:
Außerdem gibt es #Spannungstensoren, die an ihnen Verzerrungsarbeit leisten, was für die Hencky Dehnungen nicht gegeben ist.
Verzerrungsgeschwindigkeiten[Bearbeiten | Quelltext bearbeiten]
Aus der materiellen Zeitableitung
leiten sich der materielle Verzerrungsgeschwindigkeitstensor
und der räumliche
ab, die genau dann verschwinden, wenn Starrkörperbewegungen vorliegen.
Der räumliche Verzerrungsgeschwindigkeitstensor ist der symmetrische Anteil des räumlichen Geschwindigkeitsgradienten :
Geometrische Linearisierung[Bearbeiten | Quelltext bearbeiten]

Die Gleichungen der Kontinuumsmechanik für Festkörper erfahren eine erhebliche Vereinfachung, wenn kleine Verschiebungen angenommen werden können. Verschiebungen sind die Differenz der Ortsvektoren eines Partikels in der Momentankonfiguration und seiner Ausgangslage :
und der Verschiebungsgradient ist der Tensor
Wenn eine charakteristische Abmessung des Körpers ist, dann wird bei kleinen Verschiebungen sowohl als auch gefordert, so dass alle Terme, die höhere Potenzen von oder beinhalten, vernachlässigt werden können. Bei kleinen Verschiebungen ist eine Unterscheidung der Lagrange’schen und Euler’schen Betrachtungsweise nicht mehr nötig, so dass die räumlichen Koordinaten und die materiellen nicht mehr auseinandergehalten werden müssen. Dies führt zu
Das bedeutet, dass alle aufgeführten Verzerrungsmaße bei kleinen Verschiebungen in den linearisierten Verzerrungstensor übergehen. Der linearisierte Verzerrungstensor
wird auch Ingenieursdehnung genannt, denn bei vielen Anwendungen im technischen Bereich liegen kleine Dehnungen vor oder sie müssen aus sicherheitstechnischen Gründen klein gehalten werden. Diese geometrisch lineare Betrachtung ist für Werte bis 3–8 % zulässig, siehe Bild. Liegen keine kleinen Verschiebungen vor, wird von finiten oder großen Verschiebungen gesprochen.
Manchmal wird für die geometrische Linearisierung nur gefordert und fallen gelassen, so dass große Translationen bei nur kleinen Drehungen und Dehnungen erlaubt sind. Dann muss nach wie vor zwischen der Lagrange’schen und Euler’schen Betrachtungsweise unterschieden werden.
Naturgesetze[Bearbeiten | Quelltext bearbeiten]
Die in der Mechanik für ausgedehnte Körper formulierten Naturgesetze werden in der Kontinuumsmechanik als globale Integralgleichungen ausgedrückt, aus denen sich mit geeigneten Stetigkeitsannahmen lokale (Differential-)Gleichungen ableiten lassen, die an jedem materiellen Punkt erfüllt sein müssen. Mittels Äquivalenz-Umformungen der lokalen Gleichungen können anschließend weitere Prinzipien motiviert werden. Die globalen und lokalen Gleichungen können des Weiteren auf die räumlichen oder die materiellen Größen bezogen sein, so dass es für jedes Gesetz vier äquivalente Formulierungen gibt. Die hier verwendeten Formeln und weitere sind in der Formelsammlung Tensoranalysis zusammengefasst.
Die Bilanzgleichungen der Mechanik beschreiben die Wirkung der Außenwelt auf einen Körper und die daraus resultierende Änderung physikalischer Größen. Diese Größen sind die Masse, der Impuls, der Drehimpuls und die Energie. Neben den in der Mechanik bekannten äußeren Einflüssen gibt es im Kontinuum auch innere Quellen und Senken, z. B. ist die Schwerkraft eine innere Quelle für Spannungen. In abgeschlossenen Systemen, wo per definitionem eine Wechselwirkung mit der Außenwelt ausgeschlossen wird, werden aus den Bilanzgleichungen Erhaltungssätze. Der zweite Hauptsatz der Thermodynamik wird in Form der Clausius-Duhem-Ungleichung berücksichtigt.
Spannungstensoren[Bearbeiten | Quelltext bearbeiten]

Grundlegend für die Formulierung der Bilanzgleichungen ist der Begriff des Spannungstensors, der die Spannungen in Körpern auf Grund äußerer Belastungen darstellt. Das zweite Newton’sche Gesetz beschreibt die Reaktion eines Körpers auf eine äußere Kraft. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, d. h. auf einem Teil der Oberfläche des Körpers wirken Traktionsvektoren (Vektoren mit der Dimension Kraft pro Fläche) ein die sich in den Körper als Spannungen fortpflanzen. Nun kann der Körper gedanklich zerschnitten werden, so dass sich an den Schnittflächen Schnittspannungen ausbilden, die jedoch von der Orientierung der Schnittflächen, d. h. ihren Normalenvektoren, abhängen, siehe Abbildung rechts.
Aus Gleichgewichtsbedingungen ergibt sich, dass der Zusammenhang zwischen der Normalen und den Traktionsvektoren linear sein muss, was der Inhalt des Cauchy’schen Fundamentaltheorems ist:
Der Cauchy’sche Spannungstensor transformiert die Normale an die Schnittfläche in den Traktionsvektor[4]. Bei der Übertragung dieses Zusammenhangs in die Lagrange’sche Betrachtungsweise muss noch die Veränderung der Flächenelemente berücksichtigt werden:
Der Spannungstensor heißt Nennspannungstensor und repräsentiert die Spannungen bezogen auf die Ausgangsfläche. Die transponierte des Nennspannungstensors ist der erste Piola-Kirchhoff’sche Spannungstensor
Später wird noch der zweite Piola-Kirchhoff’sche Spannungstensor
benötigt.
Bei kleinen Verzerrungen braucht nicht zwischen diesen Spannungstensoren unterschieden zu werden.
Massenbilanz[Bearbeiten | Quelltext bearbeiten]
Sei die Dichte in der räumlichen und die in der materiellen Beschreibung. Unter der Annahme, dass es keine Massenquellen irgendeiner Form gibt, bedeutet die Massenbilanz, dass die Masse eines Körpers
zeitlich konstant ist:
| Lagrange’sche Betrachtungsweise | Euler’sche Betrachtungsweise | |
|---|---|---|
| globale Form | ||
| lokale Form |
Die lokalen Formen werden Kontinuitätsgleichung genannt. In der lokalen Euler’schen Formulierung wurde die Produktregel
und die materielle Zeitableitung der Dichte eingesetzt.
Impulsbilanz[Bearbeiten | Quelltext bearbeiten]
Der Impulssatz besagt, dass die Änderung des Impulses gleich der von außen angreifenden Kräfte (volumenverteilt oder oberflächlich) ist:
| Lagrange’sche Betrachtungsweise | Euler’sche Betrachtungsweise | |
|---|---|---|
| globale Form | ||
| lokale Form |
Der Vektor steht für eine massenbezogene Kraft wie die Schwerebeschleunigung, und sind Oberflächenspannungen auf der Oberfläche bzw. des Körpers in der materiellen bzw. räumlichen Darstellung.
Drehimpulsbilanz[Bearbeiten | Quelltext bearbeiten]
Der Drehimpulssatz besagt, dass die Änderung des Drehimpulses gleich der von außen angreifenden Drehmomente (volumenverteilt oder oberflächlich) ist:
| Lagrange’sche Betrachtungsweise | |
|---|---|
| Euler’sche Betrachtungsweise |
Das Rechenzeichen bildet das Kreuzprodukt und ist ein beliebiger, zeitlich fixierter Ortsvektor.
Die lokalen Formen reduzieren sich auf die Forderung nach der Symmetrie des zweiten Piola-Kirchhoff’schen und des Cauchy’schen Spannungstensors:
| Lagrange’sche Betrachtungsweise | |
|---|---|
| Euler’sche Betrachtungsweise |
Energiebilanz[Bearbeiten | Quelltext bearbeiten]
Die thermomechanische Energiebilanz besagt, dass die Änderung der Gesamtenergie eines Körpers gleich der Summe aus Wärmezufuhr und Leistung aller äußeren Kräfte ist. Die Gesamtenergie setzt sich in der Lagrange’schen Betrachtungsweise aus der inneren Energie mit der spezifischen inneren Energie und der kinetischen Energie zusammen:
Darin sind innere Wärmequellen des Körpers, der Wärmestrom pro Fläche und die auf dem Oberflächenelement des Körpers nach außen gerichtete Normale. Das negative Vorzeichen des letztens Terms liefert eine Energiezufuhr, wenn der Wärmestrom in den Körper gerichtet ist.
In der Euler’schen Betrachtungsweise heißt die globale Energiebilanz:
Die lokalen Formen lauten:
| Lagrange’sche Betrachtungsweise | |
|---|---|
| Euler’sche Betrachtungsweise |
Prinzip von d’Alembert in der Lagrange’schen Fassung[Bearbeiten | Quelltext bearbeiten]
Das Prinzip von d’Alembert in der Lagrange’schen Fassung hat eine grundlegende Bedeutung für die Lösung von Anfangsrandwertaufgaben der Kontinuumsmechanik, insbesondere der Verschiebungsmethode in der Finite-Elemente-Methode. Das Prinzip von d’Alembert in der Lagrange’schen Fassung ist eine zur lokalen Impulsbilanz (in materieller Darstellung) äquivalente Aussage über Arbeiten von im System auftretenden Kräften und Spannungen an virtuellen Verschiebungen bzw. virtuellen Verzerrungen.
Unter der Verschiebung eines materiellen Punktes in wird der Differenzvektor von seiner momentanen Lage und seiner Ausgangslage verstanden: . Virtuelle Verschiebungen sind von unabhängige, gedachte, weitgehend beliebige, differenzielle Verschiebungen, die mit den geometrischen Bindungen des Körpers verträglich sind. Die virtuellen Verschiebungen müssen verschwinden, wo immer Verschiebungsrandbedingungen des Körpers vorgegeben sind. Sei der Teil der Oberfläche des Körpers, auf dem Verschiebungsrandbedingungen erklärt sind. Für ein materielles Vektorfeld der virtuellen Verschiebungen ist dann
zu fordern. Auf können dann keine Oberflächenspannungen vorgegeben werden. Deshalb bezeichnet den Teil der Oberfläche des Körpers, auf dem Oberflächenspannungen wirken (können). Analog zu den auf den Verschiebungen basierenden Verzerrungen entwickeln sich virtuelle Verzerrungen aus den virtuellen Verschiebungen , weswegen diese mindestens einmal stetig differenzierbar sein sollen:
Darin ist der virtuelle Deformationsgradient.
Indem die lokale Impulsbilanz in der Lagrange’schen Formulierung skalar mit den virtuellen Verschiebungen multipliziert und das Ergebnis über das Volumen des Körpers integriert wird, entsteht
Die Menge enthält alle zulässigen virtuellen Verschiebungen. Weil diese Gleichung für alle möglichen virtuellen Verschiebungen gilt, verschwindet das Volumenintegral stets nur genau dann, wenn der Term in den Klammern überall verschwindet. Dies wird auch „schwache Formulierung“ der Impulsbilanz genannt. Weitere Umformung der Integralgleichung durch Ausnutzung des Cauchy’schen Fundamentaltheorems, des Gauß’schen Integralsatzes, der Produktregeln für die Divergenz und der Symmetrie des zweiten Piola-Kirchhoff Spannungstensors führt auf das Prinzip von d’Alembert in der Lagrange’schen Fassung
Auf der linken Seite steht die virtuelle Arbeit der Trägheitskräfte und die virtuelle Deformationsarbeit und auf der rechten Seite die virtuelle Arbeit der äußeren Kräfte (oberflächen- und volumenverteilt). Die genaue Herleitung ist in den Folgerungen aus den Cauchy-Euler’schen-Bewegungsgesetzen nachzuschlagen.
Clausius-Duhem-Ungleichung[Bearbeiten | Quelltext bearbeiten]
Die Clausius-Duhem-Ungleichung folgt aus der Anwendung des zweiten Hauptsatzes der Thermodynamik auf Festkörper. Mit den in quasi stationären Prozessen gerechtfertigten Annahmen der Entropieproduktion und des Entropieflusses leitet sich mit der spezifischen Entropie aus dem zweiten Hauptsatz der Thermodynamik die Clausius-Duhem-Ungleichung ab:
| Lagrange’sche Betrachtungsweise | Euler’sche Betrachtungsweise | |
|---|---|---|
| globale Form | ||
| lokale Form |
Hier ist wieder das negative Vorzeichen des letzten Terms in den globalen Formen der nach außen gerichteten Normalen geschuldet, siehe #Energiebilanz oben. Die Helmholtz’sche freie Energie:
ersetzt in den lokalen Formen die innere Energie. Im wichtigen Sonderfall, in dem Temperaturänderungen vernachlässigt werden können, vereinfachen sich die lokalen Formen zu:
| Lagrange’sche Betrachtungsweise | Euler’sche Betrachtungsweise | |
|---|---|---|
| lokale Form |
Das Skalarprodukt der Spannungen mit den Verzerrungsgeschwindigkeiten ist die spezifische Spannungsleistung und derjenige Anteil von ihr, der über die Produktion an freier Energie hinausgeht, wird dissipiert. Die lokalen Formen der Clausius-Duhem-Ungleichung sind weniger als Einschränkung physikalischer Prozesse, sondern vielmehr als Anforderung an Materialmodelle zu interpretieren: Es muss sichergestellt sein, dass die lokalen Formen der Clausius-Duhem-Ungleichung von den konstitutiven Gleichungen für beliebige Prozesse erfüllt werden.
Materialtheorie[Bearbeiten | Quelltext bearbeiten]
Die Materialtheorie beschäftigt sich mit den individuellen Merkmalen von Materialien und der Erstellung mathematischer Modelle hiervon. Ziel eines Materialmodells ist es, die wesentlichen Aspekte des Materialverhaltens zu beschreiben, wobei das was wesentlich ist, vom Beobachter festgelegt wird. Stoff- oder Materialgesetze, wie Materialmodelle manchmal genannt werden, haben nicht die allgemeine Gültigkeit physikalischer Gesetze. Zentral in der Materialmodellierung ist die Abhängigkeit der Spannungen von den Dehnungen (oder umgekehrt) in Form von Gleichungen zu beschreiben, so dass die Deformation von Körpern aus diesem Material berechnet werden kann. Die klassische Kontinuumsmechanik betrachtet vor allem einfache Materialien, deren Eigenschaften mit materiellen Zwangsbedingungen, materiellen Symmetrien und konstitutiven Gleichungen wiedergegeben werden. Dabei sind grundlegende Prinzipien zu beachten.
Grundlegende Prinzipien[Bearbeiten | Quelltext bearbeiten]
In der Materialtheorie sind Prinzipien formuliert worden, die die Konstruktion von Materialmodellen dahingehend unterstützen, dass realistische physikalische Probleme auch physikalisch realistische Lösungen haben. Eine vollständige, allgemeingültige und präzise Feststellung aller notwendigen Prinzipien ist allerdings auch Anfang des 20. Jahrhunderts noch nicht gegeben. Besonders vorzuheben sind[5]:277f[6]
- Prinzip der Determiniertheit
- Der aktuelle Zustand des Kontinuums wird durch die aktuelle Beanspruchung sowie die gesamte Vorgeschichte bestimmt.
- Axiom der lokalen Wirkung
- Der Zustand in den materiellen Punkten wird einzig durch die unmittelbare Umgebung des materiellen Punktes beeinflusst; Fernwirkungen werden entsprechend vernachlässigt.
- Prinzip der materiellen Objektivität
- Die Konstitutivgleichungen dürfen nicht von der Wahl des Bezugssystems bzw. von Bewegungen des Beobachtersystems im Raum abhängen.
Einfache Materialien[Bearbeiten | Quelltext bearbeiten]
Die klassische Kontinuumsmechanik betrachtet vor allem einfache Materialien, deren Verhalten sich mit dem Deformationsgradient beschreiben lässt. Materialien höheren Grades benutzen auch höhere Ableitungen nach den materiellen Koordinaten als die ersten, die den Deformationsgradienten ausmachen. Zudem sind einfache Materialien deterministisch, lokal und objektiv. Bei einfachen Materialien ergeben sich deshalb die Spannungen in einem materiellen Punkt aus den vergangenen Werten und dem aktuellen Wert des Green-Lagrange’schen Verzerrungstensors oder daraus ableitbaren Größen in diesem Punkt.[5]:282,6
Materielle Zwangsbedingungen[Bearbeiten | Quelltext bearbeiten]
Materielle Zwangsbedingungen stellen kinematische Nebenbedingungen dar, die die Deformationsmöglichkeiten eines Materials einschränken. Die bekannteste dieser Bedingungen ist die Inkompressibilität, die dem Material nur volumenerhaltende Verformungen erlauben, wie sie einige Flüssigkeiten oder gummielastische Materialien zeigen. Die kinematische Nebenbedingung lautet hier . Die Reaktionsspannungen im Material ergeben sich dann nicht mehr aus den Konstitutivgleichungen, sondern aus den Bilanzgleichungen und Randbedingungen. Bei Inkompressibilität z. B. ist die Reaktionsspannung der Druck im Material. Die stärkste Nebenbedingung ist die, die den Starrkörper auszeichnet. Hier entfallen alle Konstitutivgleichungen und die Spannungen sind vollständig durch die Naturgesetze und Randbedingungen bestimmt.
Materielle Symmetrien[Bearbeiten | Quelltext bearbeiten]
Materielle Symmetrien beschreiben welche Transformationen des Materials möglich sind, ohne dass sich bei gegebenem Deformationsgradient die Spannungen ändern. Diese Transformationen bilden die Symmetriegruppe des Materials. Sind alle volumenerhaltenden Transformationen erlaubt, liegt eine Flüssigkeit oder ein Gas vor. Bei Feststoffen sind nur Drehungen möglich: Bei isotropen Feststoffen sind alle Drehungen, bei transversal isotropen beliebige Drehungen um eine Achse, bei kubisch anisotropen nur 90-Grad-Drehungen um drei zueinander orthogonale Achsen, bei orthotropen nur 180-Grad-Drehungen um drei zueinander orthogonale Achsen und bei vollständig, triklin anisotropen sind nur „Drehungen“ um 0 Grad erlaubt.
Konstitutive Gleichungen[Bearbeiten | Quelltext bearbeiten]
Die konstitutiven Gleichungen geben eine Relation zwischen den Dehnungen und den Spannungen in Form von Integral-, Differential- oder algebraischen Gleichungen. Die folgenden Materialmodelle geben Beispiele für konstitutive Gleichungen.
- Ideales Gas: Beim idealen Gas ist der Druck proportional zur Dichte und Temperatur :
Die spezifische Gaskonstante ist ein Materialparameter. Dieses Materialmodell führt in Verbindung mit der Kontinuitätsgleichung und der Impulsbilanz auf die Euler-Gleichungen der Strömungsmechanik. - Linear viskoses oder newtonsches Fluid:
Die Materialparameter und sind die ersten und zweiten Lamé-Konstanten und die Spur. Dieses Materialmodell liefert in Verbindung mit der Kontinuitätsgleichung und der Impulsbilanz die Navier-Stokes-Gleichungen. - Hookesches Gesetz für linear elastische isotrope Festkörper:
.
Es ist der Schubmodul und die Querkontraktionszahl. Dieses Materialmodell ergibt in Verbindung mit der Impulsbilanz die Navier-Cauchy-Gleichungen. - Viskoelastizität:
.
Es bedeutet die Ableitung nach dem Zeitparameter , den Deviator und und sind Relaxationsfunktionen für den Schub- bzw. den volumetrischen Anteil der Deformation. - Plastizität: Bei der geschwindigkeitsunabhängigen Plastizität wird das Materialverhalten mit algebraischen und Differentialgleichungen beschrieben. Die algebraischen Gleichungen legen die additive Aufspaltung der Dehnungen in einen elastischen und einen plastischen Anteil, die Beziehung zwischen den Spannungen und den elastischen Dehnungen sowie die Fließfläche fest, die im Spannungsraum den elastischen Bereich vom plastischen Bereich trennt. Mit Differentialgleichungen wird die Entwicklung der inneren Variablen, z. B. der plastischen Dehnungen, beschrieben. In der klassischen Plastizität bleiben die Spannungen beim Fließen auf der Fließfläche.
- Viskoplastizität: Bei der geschwindigkeitsabhängigen Plastizität wird das Materialverhalten auch mit algebraischen und Differentialgleichungen dargestellt. Hier können die Spannungen jedoch zeitweilig außerhalb der Fließfläche liegen, kehren aber bei einer Relaxation auf diese zurück.
Die ersten beiden Modelle sind die in der Strömungsmechanik hauptsächlich betrachteten und die Feststoffmodelle drei bis sechs sind Repräsentanten der vier Gruppen von Modellen der klassischen Materialtheorie, die geschwindigkeitsabhängiges oder unabhängiges Verhalten mit oder ohne (Gleichgewichts-)Hysterese beschreiben.
Beispiel[Bearbeiten | Quelltext bearbeiten]

Anhand der Dehnung eines verdrehten Klotzes unter reinem Zug (siehe Bild) sollen die Gleichungen der Kontinuumsmechanik angewendet werden. Er habe in der Ausgangskonfiguration im globalen kartesischen Koordinatensystem die Länge in x-Richtung, die Breite in y-Richtung und Höhe in z-Richtung und sei im Ursprung parallel zu den Koordinatenachsen ausgerichtet. Dieser Klotz werde langgezogen, wobei sich Streckungen in materieller X-, Y- bzw. Z-Richtung einstellen, und anschließend um 90° um die z-Achse gedreht.
In der Momentankonfiguration haben die materiellen Punkte
dann die räumlichen Koordinaten
Die materiellen Linien mit und sind in der Momentankonfiguration also parallel zur y-Achse ausgerichtet. In der Momentankonfiguration entspricht ein Zug in materieller x-Richtung einem Zug in räumlicher y-Richtung.
Der Deformations- und Verschiebungsgradient berechnen sich aus der Ableitung
Wegen der Drehung um 90° ergibt sich die polare Zerlegung
Daraus bekommt man die Verzerrungstensoren:
woran man sieht, dass bei großen Drehungen die geometrisch linearen Dehnungen nicht benutzbar sind.
Unter Verwendung des Hooke’schen Gesetzes bei großen Deformationen ergeben sich die zweiten Piola Kirchhoff Spannungen im Lagrange’schen Bild:
Bei reinem Zug in materieller x-Richtung mittels erkennt man und daher
worin der xx-Koeffizient von und der Elastizitätsmodul ist. Der Nennspannungstensor lautet
mit . In der hier betrachteten Statik besagt der Impulssatz
was wegen gegeben ist. Der Cauchy’sche Spannungstensor bekommt die Form:
mit .
Der transponierte Nennspannungstensor und Cauchy’sche Spannungstensor transformieren die Normalenvektoren an den Oberflächen des Klotzes in die dort in der Ausgangs- bzw. Momentankonfiguration angreifenden Traktionsvektoren:
Die angreifende Kraft ergibt sich durch Integration der Traktion über die Stirnflächen im Ausgangs- bzw. Momentanzustand:
Drückt man den Klotz auf null Länge zusammen, so dass ist, verschwindet diese Kraft. Dies zeigt, dass das Hooke’sche Gesetz bei derart großen Verformungen nicht anwendbar ist. Das Hooke’sche Gesetz ergibt nur bei moderaten Dehnungen physikalisch plausible Antworten.
Mit bekommt man für die geometrische Linearisierung und damit die in der technischen Mechanik wohlbekannte Formel für die Schnittkraft im linear elastischen Stab mit der Querschnittsfläche
In der Ausgangskonfiguration sind die Oberflächen mit Normalen in y- und z-Richtung spannungsfrei und in der Momentankonfiguration gilt das für die Flächen mit Normalen in x- und z-Richtung:
Als Referenzkonfiguration eignet sich auch der Einheitswürfel
So bekommen die materiellen Punkte in der Ausgangskonfiguration die Koordinaten
Der zwischen der Referenz- und der Ausgangskonfiguration operierende „Deformationsgradient“ wird auch als Jacobi-Matrix bezeichnet:
Das Volumenintegral einer Feldgröße lautet dann
und kann in dieser Form numerisch mit der Gauß-Quadratur berechnet werden.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
Fußnoten[Bearbeiten | Quelltext bearbeiten]
- ↑ H. Altenbach, S. 3 ff
- ↑ F. Durst, S. 10 ff
- ↑ C. Truesdell: A First Course in Rational Continuum Mechanics. General Concepts. In: Pure and Applied Mathematics, Book Series. Band 71, Nr. 1. Science Direct, 1977, S. 3–391 (sciencedirect.com).
- ↑ Die Transposition des Spannungstensors stellt sicher, dass in seinen Koeffizienten der erste Index auf die Schnittflächennormale hinweist und der zweite Index die Wirkrichtung anzeigt.
- ↑ a b P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 978-3-642-07718-0, S. 277 f., doi:10.1007/978-3-662-04775-0.
- ↑ Altenbach, S. 218ff.
Literatur[Bearbeiten | Quelltext bearbeiten]
- H. Altenbach: Kontinuumsmechanik. Springer Verlag, 2012, ISBN 978-3-642-24118-5.
- H. Parisch: Festkörper Kontinuumsmechanik. Teubner, 2003, ISBN 3-519-00434-8.
- A. Bertram: Axiomatische Einführung in die Kontinuumsmechanik. Wissenschaftsverlag, 1989, ISBN 3-411-14031-3.
- E. Becker, W. Bürger: Kontinuumsmechanik. Teubner, 1975, ISBN 3-519-02319-9.
- F. Durst: Grundlagen der Strömungsmechanik. Springer Verlag, 2006, ISBN 3-540-31323-0.
- Ralf Greve: Kontinuumsmechanik. Springer Verlag, 2003, ISBN 3-540-00760-1.
- Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, Berlin u. a. 2000, ISBN 3-540-66114-X.
- Wolfgang H. Müller: Streifzüge durch die Kontinuumstheorie. Springer Verlag, 2011, ISBN 3-642-19869-4.
- Valentin L. Popov: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer Verlag, 2009, ISBN 978-3-540-88836-9.
- Arnold Sommerfeld: Vorlesungen über theoretische Physik. Mechanik der deformierbaren Medien. Nachdruck der 6. Auflage. Band 2. Harry Deutsch, Thun, Frankfurt/M. 1992, ISBN 3-87144-375-1.
- C. Truesdell, W. Noll: The non-linear field theories of mechanics. Springer Verlag, 1992, ISBN 3-540-55098-4.
















































































![{\displaystyle {\begin{array}{lclcl}{\dfrac {\mathrm {D} }{\mathrm {D} t}}(\mathrm {d} {\vec {x}}\cdot \mathrm {d} {\vec {y}}-\mathrm {d} {\vec {X}}\cdot \mathrm {d} {\vec {Y}})&=&{\dfrac {\mathrm {D} }{\mathrm {D} t}}[(\mathbf {F} \cdot \mathrm {d} {\vec {X}})\cdot (\mathbf {F} \cdot \mathrm {d} {\vec {Y}})]\\&=&({\dot {\mathbf {F} }}\cdot \mathrm {d} {\vec {X}})\cdot (\mathbf {F} \cdot \mathrm {d} {\vec {Y}})+(\mathbf {F} \cdot \mathrm {d} {\vec {X}})\cdot ({\dot {\mathbf {F} }}\cdot \mathrm {d} {\vec {Y}})&=:&2\mathrm {d} {\vec {X}}\cdot {\dot {\mathbf {E} }}\cdot \mathrm {d} {\vec {Y}}\\&=&({\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {x}})\cdot \mathrm {d} {\vec {y}}+\mathrm {d} {\vec {x}}\cdot ({\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {y}})&=:&2\mathrm {d} {\vec {x}}\cdot \mathbf {d} \cdot \mathrm {d} {\vec {y}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29188171ce53b233dd1ab0336c00e9b789af7a05)







![{\displaystyle \mathbf {H} =\operatorname {GRAD} \;{\vec {u}}=\mathbf {F} -\mathbf {1} =\left({\begin{array}{ccc}{\frac {\partial u}{\partial X}}&{\frac {\partial u}{\partial Y}}&{\frac {\partial u}{\partial Z}}\\[1ex]{\frac {\partial v}{\partial X}}&{\frac {\partial v}{\partial Y}}&{\frac {\partial v}{\partial Z}}\\[1ex]{\frac {\partial w}{\partial X}}&{\frac {\partial w}{\partial Y}}&{\frac {\partial w}{\partial Z}}\end{array}}\right)\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1613716056ac01926293092aab86bd1796276ee2)







![{\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\top })=\left({\begin{array}{ccc}{\frac {\partial u}{\partial x}}&{\frac {1}{2}}\left({\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}}\right)\\[1ex]{\frac {1}{2}}\left({\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}\right)&{\frac {\partial v}{\partial y}}&{\frac {1}{2}}\left({\frac {\partial v}{\partial z}}+{\frac {\partial w}{\partial y}}\right)\\[1ex]{\frac {1}{2}}\left({\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial v}{\partial z}}+{\frac {\partial w}{\partial y}}\right)&{\frac {\partial w}{\partial z}}\end{array}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60329f340927f55993c0e08695ebbaac01986047)













































































![{\displaystyle {\boldsymbol {\sigma }}=2\int _{0}^{t}\gamma (t-\tau ){\boldsymbol {\varepsilon }}(\tau )'^{\mathrm {D} }\,\mathrm {d} \tau +\int _{0}^{t}\kappa (t-\tau )\operatorname {Sp} [{\boldsymbol {\varepsilon }}(\tau ){\text{'}}]\,\mathrm {d} \tau \mathbf {I} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6de3de182919f155b956e30baeb762926c9122c0)









![{\displaystyle {\vec {X}}=(X,Y,Z)^{\top }\in [0,L]\times [0,B]\times [0,H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af186daf2ad45a3fa4253e538ab51688e7e3a91d)

![{\displaystyle X\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ce6ad49ed11491569dfa738e0f61a9b0c73fed9)




![{\displaystyle {\begin{aligned}{\tilde {\mathbf {T} }}=&2G\left[\mathbf {E} +{\frac {\nu }{1-2\nu }}\operatorname {Sp} (\mathbf {E} )\mathbf {1} \right]\\=&2G\left[{\frac {1}{2}}{\scriptstyle {\begin{pmatrix}\lambda ^{2}-1&0&0\\0&{\beta }^{2}-1&0\\0&0&{\eta }^{2}-1\end{pmatrix}}}+{\frac {\nu (\lambda ^{2}+\beta ^{2}+\eta ^{2}-3)}{2(1-2\nu )}}{\scriptstyle {\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/778416a7f5c221165632f0a2050edcf106ae5be9)






















![{\displaystyle (\Theta _{1},\Theta _{2},\Theta _{3})\in {[-1,1]}^{3}\subset \mathbb {V} ^{3}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50f7dcfc0d28a95f15b6ecd94a5c0d7f408747ca)




