„Alpha-stabile Verteilungen“ – Versionsunterschied

Versionsgeschichte interaktiv durchsuchen

[gesichtete Version]

← Zum vorherigen Versionsunterschied Zum nächsten Versionsunterschied →

Inhalt gelöscht Inhalt hinzugefügt

VisuellWikitext

Inline

Version vom 3. Juli 2023, 18:55 Uhr

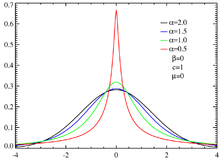
Die Familie der α-stabilen Verteilungen ist eine Verteilungsklasse von stetigen Wahrscheinlichkeitsverteilungen aus der Stochastik, die durch folgende definierende Eigenschaft beschrieben werden: sind $X_{1},X_{2},\dotsc ,X_{n},X$ unabhängige, identisch verteilte Zufallsvariablen, und gilt für die Summe

X_{1}+X_{2}+\dotsb +X_{n}\sim c_{n}X

für alle

n\in \mathbb {N}

und eine Folge

(c_{n})_{n\in \mathbb {N} }

,

so nennt man $X$ stabil verteilt, wobei $\sim$ als „hat dieselbe Verteilung wie“ zu lesen ist. Man kann zeigen, dass die einzig mögliche Wahl $c_{n}=n^{1/\alpha },\alpha \in (0,2]$ ist. Die reelle Zahl $\alpha$ nennt man hierbei den Formparameter. Da die Theorie der stabilen Verteilungen maßgeblich durch Paul Lévy mitgestaltet wurde, nennt man jene Verteilungen deshalb auch manchmal Lévy-stabile Verteilungen.

Für diskrete Verteilungen gibt es den Begriff der diskreten stabilen Verteilung, ein Beispiel einer solchen Verteilung ist die Poisson-Verteilung.

Beispiele

Obwohl die stabilen Verteilungen für jedes $\alpha$ des obigen Intervalls wohldefiniert sind, ist nur für wenige spezielle Werte von α die Dichte explizit gegeben:

Die Normalverteilung mit Erwartungswert 0 ist stabil mit Formparameter $\alpha =2$ , denn bekanntlich gilt

X_{1},X_{2},\ldots ,X_{n}\sim {\mathcal {N}}(0,\sigma ^{2})\Rightarrow \sum _{i=1}^{n}X_{i}\sim {\mathcal {N}}(0,n\sigma ^{2})\sim n^{1/2}{\mathcal {N}}(0,\sigma ^{2})

. Die Normalverteilung ist die einzige Verteilung mit dem Formparameter

\alpha =2

.

Die zentrierte Cauchy-Verteilung erfüllt die Gleichung

X_{1},X_{2},\ldots ,X_{n}\sim {\rm {Cauchy}}(0,a)\Rightarrow \sum _{i=1}^{n}X_{i}\sim n\,{\rm {Cauchy}}(0,a)

sie ist also stabil mit Formparameter

\alpha =1

.

Die (eigentliche) Standard-Lévy-Verteilung ist stabil mit $\alpha ={\frac {1}{2}}$ .

Eigenschaften

Die charakteristische Funktion einer α-stabilen Verteilung ist durch

\psi _{\alpha ,\beta ,c,\mu }(t)={\begin{cases}\exp \left(i\mu t-c|t|^{\alpha }\left(1-i\beta \tan \left({\frac {\pi \alpha }{2}}\right)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha \in (0,1)\cup (1,2]\\\exp \left(i\mu t-c|t|\left(1+i\beta {\frac {2}{\pi }}\ln(|t|)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha =1\end{cases}}

gegeben^[1]^[2] Der Parameter

\alpha \in (0,2]

heißt charakteristischer Exponent. Der Parameter

\beta \in [-1,1]

heißt Schiefeparameter. Der Parameter

c

ist positiv. Der Parameter

\mu \in \mathbb {R}

ist ein Lageparameter.

Endliche Varianz existiert nur für $\alpha =2$ . Dies folgt unmittelbar aus dem zentralen Grenzwertsatz. Für $\alpha =2$ spezialisert sich die charakteristische Funktion zu $\exp(i\mu t-ct^{2})$ ; dies ist charakteristische Funktion einer Normalverteilung mit dem Erwartungswert $\mu$ und der Varianz $2c$ .
Für $1<\alpha \leq 2$ hat die Verteilung den Erwartungswert $\mu$ , für $\alpha \leq 1$ existiert kein Erwartungswert. Dies folgt mit dem Gesetz der großen Zahlen.
Alle α-stabilen Verteilungen sind unendlich teilbar und selbstähnlich („selfdecomposable“).

Literatur

Achim Klenke: Wahrscheinlichkeitstheorie. 2. Auflage. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76317-8, Kap. 16.

Einzelnachweise

↑ Paul Embrechts, Thomas Mikosch, Claudia Klüppelberg: Modelling extremal events (= Stochastic Modelling and Applied Probability. Band 33). Springer-Verlag, Berlin / Heidelberg / New York 1997, ISBN 3-540-60931-8, Theorem 2.2.3, S. 71, doi:10.1007/978-3-642-33483-2.
↑ Rick Durrett: Probability: Theory and Examples. 4. Auflage. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76539-8, S. 141.

[1] Paul Embrechts, Thomas Mikosch, Claudia Klüppelberg: Modelling extremal events (= Stochastic Modelling and Applied Probability. Band 33). Springer-Verlag, Berlin / Heidelberg / New York 1997, ISBN 3-540-60931-8, Theorem 2.2.3, S. 71, doi:10.1007/978-3-642-33483-2.

[2] Rick Durrett: Probability: Theory and Examples. 4. Auflage. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76539-8, S. 141.

[1]

[2]

@@ Zeile 20: / Zeile 20: @@
 == Eigenschaften ==
+[[Datei:Levyskew distributionPDF.png|miniatur|Dichtefunktionen α-stabiler Verteilungen für unterschiedliche Werte des Schiefeparameters <math>\beta</math> und Parameterwerte <math>\alpha = 0.5</math>, <math>c = 1</math> und <math>\mu = 0</math>]]
+* Die [[charakteristische Funktion (Stochastik)|charakteristische Funktion]] einer α-stabilen Verteilung ist durch
-[[Datei:Levyskew distributionPDF.png|miniatur|α-stabile Verteilungen für unterschiedliche Werte des Schiefeparameters]]
+:: <math>\psi_{\alpha, \beta, c,\mu}(t)= \begin{cases}\exp\left(i \mu t- c |t|^\alpha \left(1-i \beta \tan\left(\frac{\pi \alpha}{2}\right) \sgn(t)\right)\right)&\text{für } \alpha \in (0,1)\cup (1,2]\\
-* Die [[charakteristische Funktion (Stochastik)|charakteristische Funktion]] einer α-stabilen Verteilung ist für <math>\alpha \neq 1</math> gegeben durch<ref>[[Rick Durrett]]: ''Probability: Theory and Examples.'' 4. Auflage. Cambridge University Press, Cambridge u.&nbsp;a. 2010, ISBN 978-0-521-76539-8, S. 141.</ref>
-:: <math>\psi_{\alpha, \beta}(u)=\exp\left(-|u|^\alpha \left(1-i \beta \tan\left(\frac{\pi \alpha}{2}\right) \sgn(u)\right)\right)</math>.
+\exp\left(i \mu t - c|t| \left(1 + i \beta \frac{2}{\pi}\ln(|t|)  \sgn(t)\right)\right)&\text{für }  \alpha = 1 \end{cases}
+ </math>
+: gegeben<ref>{{Literatur |Autor=Paul Embrechts, Thomas Mikosch, [[Claudia Klüppelberg]] |Titel=Modelling extremal events |Reihe=Stochastic Modelling and Applied Probability |BandReihe=33 |Verlag=Springer-Verlag |Ort=Berlin / Heidelberg / New York |Datum= 1997 |ISBN=3-540-60931-8 |DOI=10.1007/978-3-642-33483-2 |Fundstelle=Theorem 2.2.3, S. 71}}</ref><ref>[[Rick Durrett]]: ''Probability: Theory and Examples.'' 4. Auflage. Cambridge University Press, Cambridge u.&nbsp;a. 2010, ISBN 978-0-521-76539-8, S. 141.</ref> Der Parameter <math>\alpha \in (0,2]</math> heißt ''charakteristischer Exponent''. Der Parameter <math>\beta \in [-1,1] </math> heißt ''Schiefeparameter''. Der Parameter <math>c</math> ist positiv.  Der Parameter <math>\mu \in \R</math> ist ein Lageparameter.
-:Der Parameter <math>\beta \in [-1,1] </math> ist hierbei frei wählbar und heißt ''Schiefeparameter''.
+* Endliche [[Varianz (Stochastik)|Varianz]] existiert nur für <math>\alpha=2</math>. Dies folgt unmittelbar aus dem [[Zentraler Grenzwertsatz|zentralen Grenzwertsatz]]. Für <math>\alpha = 2</math> spezialisert sich die charakteristische Funktion zu <math>\exp(i\mu t - ct^2)</math>; dies ist  charakteristische Funktion  einer Normalverteilung mit dem Erwartungswert <math> \mu</math> und der Varianz  <math> 2c</math>.
+* Für <math>1<\alpha\leq2</math> hat die Verteilung den [[Erwartungswert]] <math>\mu </math>, für <math>\alpha\leq1</math> existiert kein Erwartungswert. Dies folgt mit dem [[Gesetz der großen Zahlen]].
-:Für <math>\alpha = 1</math> ergibt sich
-::<math>\psi_{\alpha, \beta}(u)=\exp\left(-|u| \left(1+i \beta \frac{2}{\pi}\log(|u|) \sgn(u)\right)\right)</math>.
-* Endliche [[Varianz (Stochastik)|Varianz]] existiert nur für <math>\alpha=2</math>. Dies folgt unmittelbar aus dem [[Zentraler Grenzwertsatz|zentralen Grenzwertsatz]].
-* Für <math>1<\alpha\leq2</math> hat die Verteilung den [[Erwartungswert]] 0, für <math>\alpha\leq1</math> existiert kein Erwartungswert. Dies folgt mit dem [[Gesetz der großen Zahlen]].
 * Alle α-stabilen Verteilungen sind [[Unendliche Teilbarkeit|unendlich teilbar]] und ''selbstähnlich'' („selfdecomposable“).

„Alpha-stabile Verteilungen“ – Versionsunterschied

Version vom 3. Juli 2023, 18:55 Uhr

Inhaltsverzeichnis

Beispiele

Eigenschaften

Literatur

Einzelnachweise

Navigationsmenü

„Alpha-stabile Verteilungen“ – Versionsunterschied

Version vom 3. Juli 2023, 18:55 Uhr

Beispiele

Eigenschaften

Literatur

Einzelnachweise

Navigationsmenü

Suche