Stetige Gleichverteilung
Die stetige Gleichverteilung, auch Rechteckverteilung, kontinuierliche Gleichverteilung oder Uniformverteilung genannt, ist eine stetige Wahrscheinlichkeitsverteilung. Sie hat auf einem Intervall eine konstante Wahrscheinlichkeitsdichte. Dies ist gleichbedeutend damit, dass alle Teilintervalle gleicher Länge dieselbe Wahrscheinlichkeit besitzen.
Die Möglichkeit, die stetige Gleichverteilung auf dem Intervall von 0 bis 1 zu simulieren, bildet die Basis zur Erzeugung zahlreicher beliebig verteilter Zufallszahlen mittels der Inversionsmethode oder der Verwerfungsmethode.
Definition[Bearbeiten | Quelltext bearbeiten]
Eine stetige Zufallsvariable bezeichnet man als gleichverteilt auf dem Intervall , wenn Dichtefunktion und Verteilungsfunktion gegeben sind als

| |

|
Als abkürzende Schreibweise für die stetige Gleichverteilung wird häufig oder verwendet. In einigen Formeln sieht man auch oder als Bezeichnung für die Verteilung. Die stetige Gleichverteilung ist durch ihre ersten beiden zentralen Momente komplett beschrieben, d. h. alle höheren Momente sind aus Erwartungswert und Varianz berechenbar.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Wahrscheinlichkeiten[Bearbeiten | Quelltext bearbeiten]
Die Wahrscheinlichkeit, dass eine auf gleichverteilte Zufallsvariable in einem Teilintervall liegt, ist gleich dem Verhältnis der Intervalllängen:
- .
Erwartungswert und Median[Bearbeiten | Quelltext bearbeiten]
Der Erwartungswert und der Median der stetigen Gleichverteilung sind gleich der Mitte des Intervalls :
- .
Varianz[Bearbeiten | Quelltext bearbeiten]
Die Varianz der stetigen Gleichverteilung ist
Standardabweichung und weitere Streumaße[Bearbeiten | Quelltext bearbeiten]
Aus der Varianz erhält man die Standardabweichung
- .
Die mittlere absolute Abweichung beträgt , und der Interquartilsabstand ist genau doppelt so groß. Die Gleichverteilung ist die einzige symmetrische Verteilung mit monotoner Dichte mit dieser Eigenschaft.
Variationskoeffizient[Bearbeiten | Quelltext bearbeiten]
Für den Variationskoeffizienten ergibt sich:
- .
Symmetrie[Bearbeiten | Quelltext bearbeiten]
Die stetige Gleichverteilung ist symmetrisch um .
Schiefe[Bearbeiten | Quelltext bearbeiten]
Die Schiefe lässt sich darstellen als
- .
Wölbung und Exzess[Bearbeiten | Quelltext bearbeiten]
Die Wölbung und der Exzess lassen sich ebenfalls geschlossen darstellen als
- bzw.
- .
Momente[Bearbeiten | Quelltext bearbeiten]
| -tes Moment | |
| -tes zentrales Moment |
Summe gleichverteilter Zufallsvariablen[Bearbeiten | Quelltext bearbeiten]
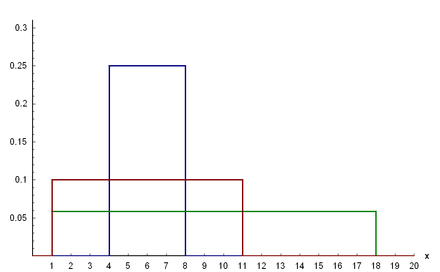
Die Summe zweier unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt, falls die Breite der beiden Träger identisch ist. Unterscheiden sich die Trägerbreiten, so ergibt sich eine trapezförmige Verteilung. Genauer:
Zwei Zufallsvariablen seien unabhängig und stetig gleichverteilt, die eine auf dem Intervall , die andere auf dem Intervall . Sei und . Dann hat ihre Summe die folgende Trapezverteilung:
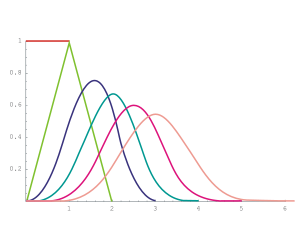
Die Summe von unabhängigen gleichverteilten Zufallsvariablen auf dem Intervall [0;1] ist eine Irwin-Hall-Verteilung, sie nähert sich der Normalverteilung an (Zentraler Grenzwertsatz).
Eine zuweilen verwendete Methode (Zwölferregel) zur approximativen Erzeugung (standard-)normalverteilter Zufallszahlen funktioniert so: man summiert 12 (unabhängige) auf dem Intervall [0,1] gleichverteilte Zufallszahlen und subtrahiert 6 (das liefert die richtigen Momente, da die Varianz einer U(0,1)-verteilten Zufallsvariablen 1/12 ist und sie den Erwartungswert 1/2 besitzt).
Charakteristische Funktion[Bearbeiten | Quelltext bearbeiten]
Die charakteristische Funktion hat die Form
- ,
wobei die imaginäre Einheit darstellt.
Momenterzeugende Funktion[Bearbeiten | Quelltext bearbeiten]
Die momenterzeugende Funktion der stetigen Gleichverteilung ist
und speziell für und
Beziehung zu anderen Verteilungen[Bearbeiten | Quelltext bearbeiten]
Beziehung zur Dreiecksverteilung[Bearbeiten | Quelltext bearbeiten]
Die Summe von zwei unabhängigen und stetig gleichverteilten Zufallsvariablen hat eine Dreiecksverteilung.
Beziehung zur Betaverteilung[Bearbeiten | Quelltext bearbeiten]
Sind unabhängige auf stetig gleichverteilte Zufallsvariable, dann haben die Ordnungsstatistiken eine Betaverteilung. Genauer gilt
für .
Simulation von Verteilungen aus der stetigen Gleichverteilung[Bearbeiten | Quelltext bearbeiten]
Mit der Inversionsmethode lassen sich gleichverteilte Zufallszahlen in andere Verteilungen überführen. Wenn eine gleichverteilte Zufallsvariable ist, dann genügt beispielsweise der Exponentialverteilung mit dem Parameter .
Verallgemeinerung auf höhere Dimensionen[Bearbeiten | Quelltext bearbeiten]
Die stetige Gleichverteilung lässt sich vom Intervall auf beliebige messbare Teilmengen des mit Lebesgue-Maß verallgemeinern. Man setzt dann
für messbare .
Diskreter Fall[Bearbeiten | Quelltext bearbeiten]
Die Gleichverteilung ist auch auf endlichen Mengen definiert, dann heißt sie diskrete Gleichverteilung.
Beispiel für das Intervall [0, 1][Bearbeiten | Quelltext bearbeiten]
Häufig wird und angenommen, also betrachtet. Dann ist die Dichtefunktion auf dem Intervall konstant gleich 1 und für die Verteilungsfunktion gilt dort . Der Erwartungswert beträgt dementsprechend , die Varianz und die Standardabweichung , wobei die letztgenannten beiden Werte auch für beliebige Intervalle der Länge 1 gelten. Siehe hierzu auch den obigen Abschnitt Summe gleichverteilter Zufallsvariablen.
Ist eine -verteilte Zufallsvariable, dann ist
-verteilt.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Christian Hesse: Angewandte Wahrscheinlichkeitstheorie. 1. Auflage. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2, S. 155–156, doi:10.1007/978-3-663-01244-3.



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![{\displaystyle [c,d]\subseteq [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c4b90060cfad2522da60caeab608de43226f6e)

















![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)


![{\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,x\longmapsto {\begin{cases}0&x\not \in [a+c,b+d]\\{\frac {x}{\alpha \beta }}-{\frac {a+c}{\alpha \beta }}&x\in [a+c,a+c+\alpha ]\\{\frac {1}{\beta }}&x\in [a+c+\alpha ,a+c+\beta ]\\{\frac {b+d}{\alpha \beta }}-{\frac {x}{\alpha \beta }}&x\in [a+c+\beta ,b+d]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3873fa7a21bbd83e45689defa7c5dd2cf85458bf)







![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
















![{\displaystyle [a,a+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b53692e0b256c365ff55b9d84ac933484c3c09f6)

