Verallgemeinerte Binomialverteilung

Verallgemeinerte Binomialverteilung
Wahrscheinlichkeitsfunktion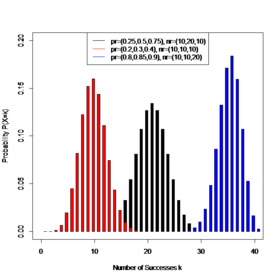
Verteilungsfunktion
Parameter	$\mathbf {p} \in [0,1]^{n}$ — Erfolgswahrscheinlichkeiten für jeden der n Versuche
Träger	$k\in \{0,\dots ,n\}$
Dichtefunktion	$\sum \limits _{A\in B_{k}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}(1-p_{j})$
Verteilungsfunktion	$\sum \limits _{l=0}^{k}\sum \limits _{A\in B_{l}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}{(1-p_{j})}$
Erwartungswert	$\sum \limits _{i=1}^{n}p_{i}$
Varianz	$\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}}$
Schiefe	${\frac {\sum \limits _{i=1}^{n}{\left(1-2{p_{i}}\right)\left(1-{{p}_{i}}\right){{p}_{i}}}}{(\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}})^{\frac {3}{2}}}}$
Wölbung	$3+{\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}})^{4}}}$
Momenterzeugende Funktion	$\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{t}})$
Charakteristische Funktion	$\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{it}})$

Die Verallgemeinerte Binomialverteilung (gelegentlich auch Poissonsche Verallgemeinerung der Binomialverteilung, oder Poisson-Binomialverteilung genannt) ist eine Wahrscheinlichkeitsverteilung und somit dem mathematischen Teilgebiet der Stochastik zuzuordnen. Bei ihr handelt es sich um eine univariate diskrete Wahrscheinlichkeitsverteilung. Sie ist definiert als die Summe von unabhängigen, nicht notwendigerweise identisch verteilten Zufallsvariablen, welche einer Bernoulli-Verteilung unterliegen.

Die Verallgemeinerte Binomialverteilung beschreibt also die Erfolge einer Serie von unabhängigen Versuchen, welche jeweils genau zwei Ergebnisse annehmen kann. Der Unterschied zur Binomialverteilung besteht darin, dass jedem Versuch eine andere Erfolgswahrscheinlichkeit zugeordnet werden kann.

Es ist auch möglich die Verallgemeinerte Binomialverteilung als Summe von unabhängigen, nicht identischen, binomialverteilten Zufallsvariablen festzulegen, wobei die Bernoulli Zufallsgrößen mit identischen Erfolgswahrscheinlichkeiten zu binomialverteilten Zufallsvariablen zusammengefasst werden.

Definition der Verallgemeinerten Binomialverteilung

Eine diskrete Zufallsvariable $X$ folgt einer Verallgemeinerten Binomialverteilung mit Parametervektor $p$, wenn sie die folgende Wahrscheinlichkeitsfunktion besitzt

$\rho _{X}(k)=\sum \limits _{A\in B_{k}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}(1-p_{j})$,

wobei $p=(p_{1},\dots ,p_{n})$ den Vektor der Erfolgswahrscheinlichkeiten pro Versuch und $k$ die Gesamtanzahl der Erfolge bei $n$ Versuchen bezeichnet.

Schreibweise: $X\sim GB(p)$

$B_{k}$ ist die Menge aller $k$-elementigen Teilmengen, die aus dem Träger $\{1,2,\dots ,n\}$ gebildet werden können. $A^{c}$ ist das Komplement von $A$, das heißt $A^{c}=\{1,2,\dots ,n\}\backslash A$.

Die zugehörige Verteilungsfunktion lautet

$F_{X}(k)=P(X\leq k)=\sum \limits _{l=0}^{k}\sum \limits _{A\in B_{l}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}{(1-p_{j})}$

Alternative Parametrisierung

Die Verallgemeinerte Binomialverteilung kann ebenso als Summe von binomialverteilten Zufallsgrößen definiert werden, indem die Bernoulli Zufallsvariablen mit gleichen Erfolgswahrscheinlichkeiten zu binomialverteilten Zufallsgrößen zusammengefasst werden.

$GB(k|p)=GB(k|pr,nr)$,

wobei der Parametervektor $pr=(pr_{1},\dots ,pr_{r})$ die Erfolgswahrscheinlichkeiten von $r$ binomialverteilten Zufallsvariablen enthält und der Parametervektor $nr=(nr_{1},\dots ,nr_{r})$ die jeweils zugehörige Anzahl an Versuchen.

Es gilt somit $p=(p_{1},\dots ,p_{n})=(pr_{1}\cdot 1_{nr_{1}}^{T},\dots ,pr_{r}\cdot 1_{nr_{r}}^{T})$. Hierbei ist $1_{nr_{i}}^{T}$ der Einsvektor der Länge $nr_{i}$, bestehend aus lauter Einsen.

Eigenschaften der Verallgemeinerten Binomialverteilung

$X$ sei im Folgenden eine Zufallsvariable, die einer Verallgemeinerten Binomialverteilung folgt $X\sim GB(p)$.

Erwartungswert

Die Verallgemeinerte Binomialverteilung besitzt den Erwartungswert

$E(X)=\sum \limits _{i=1}^{n}p_{i}$

Varianz

Die Verallgemeinerte Binomialverteilung besitzt die Varianz

$Var(X)=\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}}$

Schiefe

Die Verallgemeinerte Binomialverteilung besitzt die Schiefe

$v(X)={\frac {\sum \limits _{i=1}^{n}{\left(1-2{p_{i}}\right)\left(1-{{p}_{i}}\right){{p}_{i}}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{\frac {3}{2}}}}$

Wölbung und Exzess

Die Verallgemeinerte Binomialverteilung besitzt die Wölbung

$\beta _{2}=3+{\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{2}}}$

und damit den Exzess

$\gamma =\beta _{2}-3={\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{2}}}$

Kumulanten

Die kumulantenerzeugende Funktion ist

$g_{X}(t)=\sum _{i=1}^{n}\ln(1-p_{i}+p_{i}e^{t})$.

Daher ist die k-te Kumulante genau die Summe der k-ten Kumulanten der n Bernoulli-verteilten Zufallsvariablen, aus denen die Verallgemeinerte Binomialverteilung zusammengesetzt ist:

$\tau _{k}=\tau _{k}^{1}+\dots +\tau _{k}^{n}$

Für diese Kumulanten gilt dann auch die Rekursionsgleichung der Kumulanten der Bernoulli-Verteilung.

Wahrscheinlichkeitserzeugende Funktion

Die wahrscheinlichkeitserzeugende Funktion der verallgemeinerten Binomialverteilung lautet

$m_{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{t})$

Charakteristische Funktion

Die charakteristische Funktion der Verallgemeinerten Binomialverteilung lautet:

$\varphi _{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{it}})$

Momenterzeugende Funktion

Die momenterzeugende Funktion der Verallgemeinerten Binomialverteilung lautet:

$M_{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{t}})$

Summe von verallgemeinert binomialverteilten Zufallsvariablen

Ist $X\sim GB_{n}(p_{1},\dots p_{n})$ und $Y\sim GB_{m}(p_{1},\dots p_{m})$ zwei unabhängige verallgemeinert binomialverteilte Zufallsvariablen, dann ist auch $X+Y$ verallgemeinert binomialverteilt: $X+Y\sim GB_{n+m}(p_{1},\dots p_{n+m})$. Demnach ist die verallgemeinerte Binomialverteilung reproduktiv.

Beziehung zu anderen Verteilungen

Beziehung zur Binomialverteilung

Die Summe von voneinander unabhängigen binomialverteilten Zufallsvariablen $X_{i}\sim B(n_{i},p_{i})$ ist verallgemeinert binomialverteilt. Wenn alle Erfolgswahrscheinlichkeiten gleich sind, das heißt $p_{i}=p_{j}\;\forall i,j=1\dots ,n$, dann ergibt sich aus der Verallgemeinerten Binomialverteilung die Binomialverteilung. Tatsächlich ist die Binomialverteilung für festen Erwartungswert und feste Ordnung diejenige verallgemeinerte Binomialverteilung mit maximaler Entropie. Das bedeutet, unter der Bedingung, dass der Parametervektor $p$ von $X\sim GB(p)$ die Länge $n$ hat, maximiert $p=(E(X)/n,\dots ,E(X)/n)$ die Entropie $\mathrm {H} (X)$.

Beziehung zur Bernoulli-Verteilung

Die Summe von $n$ voneinander unabhängigen Bernoulli-verteilten Zufallsvariablen $X_{i}$, die alle einen unterschiedlichen Parameter $p_{i}$ besitzen, ist verallgemeinert binomialverteilt.

Approximation durch die Poisson-Verteilung

→ Hauptartikel: Poisson-Approximation

Für eine sehr große Anzahl an Versuchen $n$ und sehr kleine, aber unterschiedliche Erfolgswahrscheinlichkeiten $p_{1},\dots ,p_{n}$ kann die Wahrscheinlichkeitsfunktion der Verallgemeinerten Binomialverteilung durch die Poisson-Verteilung approximiert werden.

$\rho _{X}(k)\approx {\frac {\lambda ^{k}}{k!}}\cdot \mathrm {e} ^{-\lambda }$

Der Parameter $\lambda$ ist gleich dem Erwartungswert der Verallgemeinerten Binomialverteilung.

Approximation durch die Normalverteilung

Die Verteilungsfunktion der Verallgemeinerten Binomialverteilung kann für eine sehr große Anzahl an Versuchen $n$ durch die Normalverteilung approximiert werden.

$F_{X}(k)\approx \Phi \left({\frac {k+0{,}5-\mu }{\sigma }}\right),\ k=0,\dots ,n$

Der Parameter $\mu$ entspricht dem Erwartungswert und $\sigma$ der Standardabweichung der Verallgemeinerten Binomialverteilung. $\Phi (\cdot )$ ist die Verteilungsfunktion der Standardnormalverteilung.

Beispiele

Radarkontrolle

Ein Arbeitnehmer muss an jedem Arbeitstag über die Autobahn und durch das Ortsgebiet zur Arbeit fahren. Die Wahrscheinlichkeiten in eine Radarkontrolle zu geraten sind $0{,}5\,\%$ auf der Autobahn und $1\,\%$ im Ortsgebiet.

Wie hoch sind die Wahrscheinlichkeiten an einem Arbeitstag in $0,1,2$ Kontrollen zu geraten?

Die zufällige Anzahl von Radarkontrollen $R$ kann als Summe von zwei Bernoulli-verteilten Zufallsvariablen $R_{1}$ für die Autobahn und $R_{2}$ für das Ortsgebiet modelliert werden: $R=R_{1}+R_{2}$, mit

$R_{1}={\begin{cases}1,&{\text{Kontrolle mit Wahrscheinlichkeit }}0{,}005\\0,&{\text{keine Kontrolle mit Wahrscheinlichkeit }}0{,}995\end{cases}}$

$R_{2}={\begin{cases}1,&{\text{Kontrolle mit Wahrscheinlichkeit }}0{,}01\\0,&{\text{keine Kontrolle mit Wahrscheinlichkeit }}0{,}99\end{cases}}$

Da $R_{1}$ und $R_{2}$ unterschiedliche Erfolgswahrscheinlichkeiten besitzen, kann man dieses Beispiel nicht mit Hilfe der Binomialverteilung lösen.

$R$ folgt einer Verallgemeinerten Binomialverteilung mit Parametervektor $p=(0{,}005,0{,}01)$.

Die gesuchten Wahrscheinlichkeiten können folgendermaßen berechnet werden:

• $0$ Kontrollen: $P(R=0)$

$P(R=0)=P(R_{1}=0)\cdot P(R_{2}=0)=0{,}995\cdot 0{,}99=0{,}98505=98{,}505\,\%$

• $1$ Kontrolle: $P(R=1)$

$P(R=1)=P(R_{1}=1)\cdot P(R_{2}=0)+P(R_{1}=0)\cdot P(R_{2}=1)=0{,}005\cdot 0{,}99+0{,}995\cdot 0{,}01=0{,}0149=1{,}49\,\%$

• $2$ Kontrollen: $P(R=2)$

$P(R=2)=P(R_{1}=1)\cdot P(R_{2}=1)=0{,}005\cdot 0{,}01=0{,}00005=0{,}005\,\%$

Herstellungsprozess

In einer Fabrik werden Geräte produziert und anschließend einer Qualitätskontrolle unterzogen. Es können $3$ verschiedene Fehlertypen auftreten. Die Wahrscheinlichkeiten, dass ein spezieller Fehlertyp auftritt sind $4\,\%$ für den Fehler vom Typ $1$ und jeweils $7\,\%$ für die Fehlertypen $2$ und $3$.

Wie hoch sind die Wahrscheinlichkeiten dafür, dass ein Gerät mit $0,1,2,3$ Fehlern produziert wird?

Die zufällige Anzahl von Fehlern $F$ kann als Summe von drei Bernoulli-verteilten Zufallsvariablen $F_{1}$, $F_{2}$ und $F_{3}$ geschrieben werden: $F=F_{1}+F_{2}+F_{3}$, mit

$F_{1}={\begin{cases}1,&{\text{Fehler mit Wahrscheinlichkeit }}0{,}04\\0,&{\text{kein Fehler mit Wahrscheinlichkeit }}0{,}96\end{cases}}$

$F_{2}=F_{3}={\begin{cases}1,&{\text{Fehler mit Wahrscheinlichkeit }}0{,}07\\0,&{\text{kein Fehler mit Wahrscheinlichkeit }}0{,}93\end{cases}}$

$F$ besitzt eine Verallgemeinerten Binomialverteilung mit Parametervektor $p=(0{,}04,0{,}07,0{,}07)$.

Alternativ kann die Parametrisierung $pr=(0{,}04,0{,}07),\ nr=(1,2)$ gewählt werden, indem die identischen Bernoulli Zufallsvariablen zu einer binomialverteilten Zufallsvariable zusammengefasst werden.

Die gesuchten Wahrscheinlichkeiten können folgendermaßen berechnet werden:

• $0$ Fehler: $P(F=0)$

$P(F=0)=P(F_{1}=0)\cdot P(F_{2}=0)\cdot P(F_{3}=0)=0{,}96\cdot 0{,}93\cdot 0{,}93=0{,}830304=83{,}0304\,\%$

• $1$ Fehler: $P(F=1)$

${\begin{aligned}P(F=1)&=P(F_{1}=1)\cdot P(F_{2}=0)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=1)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=0)\cdot P(F_{3}=1)\\&=0{,}04\cdot 0{,}93\cdot 0{,}93+0{,}96\cdot 0{,}07\cdot 0{,}93+0{,}96\cdot 0{,}93\cdot 0{,}07=0{,}159588=15{,}9588\,\%\end{aligned}}$

• $2$ Fehler: $P(F=2)$

${\begin{aligned}P(F=2)&=P(F_{1}=1)\cdot P(F_{2}=1)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=1)\cdot P(F_{3}=1)+P(F_{1}=1)\cdot P(F_{2}=0)\cdot P(F_{3}=1)\\&=0{,}04\cdot 0{,}07\cdot 0{,}93+0{,}96\cdot 0{,}07\cdot 0{,}07+0{,}04\cdot 0{,}93\cdot 0{,}07=0{,}009912=0{,}9912\,\%\end{aligned}}$

• $3$ Fehler: $P(F=3)$

$P(F=3)=P(F_{1}=1)\cdot P(F_{2}=1)\cdot P(F_{3}=1)=0{,}04\cdot 0{,}07\cdot 0{,}07=0{,}000196=0{,}0196\,\%$

Anwendung & Berechnung

Die Verallgemeinerte Binomialverteilung kommt in vielen Bereichen zum Einsatz; z. B. Umfragen, Herstellungsprozesse, Qualitätssicherung. Oft wird allerdings eine Approximation benutzt, da die exakte Berechnung sehr aufwändig ist. Ohne entsprechende Software sind selbst einfache Modelle mit wenigen Bernoulli Zufallsvariablen kaum zu berechnen.

Zufallszahlen

Zur Erzeugung von Zufallszahlen kann die Inversionsmethode verwendet werden. Alternativ kann man auch $n$ Bernoulli-verteilte Zufallszahlen zu den Parametern $p_{i}$ erzeugen und diese Aufsummieren. Das Ergebnis ist dann verallgemeinert binomialverteilt.

Literatur

• M.Fisz, Wahrscheinlichkeitsrechnung und mathematische Statistik, VEB Deutscher Verlag der Wissenschaften, 1973, p. 164 ff.
• K.J. Klauer, Kriteriumsorientierte Tests, Verlag für Psychologie, Hogrefe, 1987, Göttingen, p. 208 ff.

Weblinks

• GenBinomApps – R Package. R Package zur Berechnung von Clopper Pearson Konfidenzintervallen und der verallgemeinerten Binomialverteilung. Abgerufen am 30. Juli 2015.

Einzelnachweise

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | Dirac | diskret uniform | empirisch | hypergeometrisch | kategorial | negativ hypergeometrisch | Rademacher | verallgemeinert binomial | Zipf | Zipf-Mandelbrot | Zweipunkt

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | discrete-Phase-Type | erweitert negativ binomial | Gauss-Kuzmin | gemischt Poisson | geometrisch | logarithmisch | negativ binomial | parabolisch-fraktal | Poisson | Skellam | verallgemeinert Poisson | Yule-Simon | Zeta

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Cantor | Kumaraswamy | raised Cosine | Dreieck | Trapez | U-quadratisch | stetig uniform | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi | Chi-Quadrat | Coxian | Erlang | Exponential | Extremwert | F | Fermi-Dirac | Folded normal | Fréchet | Gamma | Gamma-Gamma | verallgemeinert invers Gauß | halblogistisch | halbnormal | Hartman-Watson | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | invers Chi-Quadrat | scale-invers Chi-Quadrat | Invers Normal | Invers Gamma | Kolmogorow-Verteilung | Lévy | log-normal | log-logistisch | Maxwell-Boltzmann | Maxwell-Speed | Nakagami | nichtzentriert Chi-Quadrat | Pareto | Phase-Type | Rayleigh | relativistisch Breit-Wigner | Rice | Rosin-Rammler | shifted Gompertz | truncated normal | Type-2-Gumbel | Weibull | Wilks’ Lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | exponential Power | Fishers z | Fisher-Tippett (Gumbel) | generalized hyperbolic | Hyperbolic-secant | Landau | Laplace | alpha-stabil | logistisch | normal (Gauß) | normal-invers Gauß’sch | Skew-normal | Studentsche t | Type-1-Gumbel | Variance-Gamma | Voigt

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Dirichlet compound multinomial | Ewens | gemischt Multinomial | multinomial | multivariat hypergeometrisch | multivariat Poisson | negativmultinomial | Pólya/Eggenberger | polyhypergeometrisch

Kontinuierliche multivariate Verteilungen:
Dirichlet | GEM | generalized Dirichlet | multivariat normal | multivariat Student | normalskaliert invers Gamma | Normal-Gamma | Poisson-Dirichlet

Multivariate Matrixverteilungen:
Gleichverteilung auf der Stiefel-Mannigfaltigkeit | Invers Wishart | Matrix Beta | Matrix Gamma | Matrix invers Beta | Matrix invers Gamma | Matrix Normal | Matrix Student-t | Matrix-Von-Mises-Fisher-Verteilung | Normal-invers-Wishart | Normal-Wishart | Wishart