Hotellingsche T-Quadrat-Verteilung
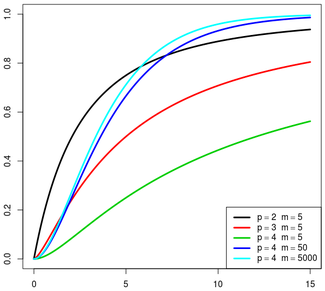
Dichtefunktion
Verteilungsfunktion
Parameter
p – Dimension der Zufallsvariablen m – verknüpft mit der Stichprobengröße
Träger
x
∈
(
0
,
+
∞
)
{\displaystyle x\in (0,+\infty )\;}
p
=
1
{\displaystyle p=1}
x
∈
[
0
,
+
∞
)
{\displaystyle x\in [0,+\infty )\;}
Die Hotellingsche T -Quadrat-Verteilung [1] Wahrscheinlichkeitsverteilung , die 1931 von Harold Hotelling erstmals beschrieben wurde.[2] Studentschen t-Verteilung .
Die quadratische Form
t
2
=
n
(
x
−
μ
)
′
W
−
1
(
x
−
μ
)
∼
T
(
p
,
n
−
1
)
{\displaystyle t^{2}=n({\mathbf {x} }-{\mathbf {\mu } })'{\mathbf {W} }^{-1}({\mathbf {x} }-{\mathbf {\mu } })\sim T(p,n-1)}
folgt einer Hotellingschen T-Quadrat-Verteilung mit
n
{\displaystyle n}
x
{\displaystyle {\mathbf {x} }}
p
{\displaystyle p}
W
{\displaystyle {\mathbf {W} }}
p
×
p
{\displaystyle p\times p}
Kovarianzmatrix Es sei
x
∼
N
p
(
μ
,
V
)
{\displaystyle x\sim N_{p}(\mu ,{\mathbf {V} })}
Zufallsvariable mit einer multivariaten Normalverteilung und
W
∼
W
p
(
m
,
V
)
{\displaystyle {\mathbf {W} }\sim W_{p}(m,{\mathbf {V} })}
x
{\displaystyle x}
Wishart-Verteilung mit einer nicht-singulären Kovarianzmatrix
V
{\displaystyle \mathbf {V} }
m
=
n
−
1
{\displaystyle m=n-1}
t
2
{\displaystyle t^{2}}
T
2
(
p
,
m
)
{\displaystyle T^{2}(p,m)}
Hotellingsche T -Quadrat-Verteilung mit Parametern
p
{\displaystyle p}
m
{\displaystyle m}
F
{\displaystyle F}
F-Verteilung . Dann kann gezeigt werden, dass gilt:
m
−
p
+
1
p
m
T
2
∼
F
p
,
m
−
p
+
1
{\displaystyle {\frac {m-p+1}{pm}}T^{2}\sim F_{p,m-p+1}}
Unter der Annahme, dass
x
1
,
…
,
x
n
{\displaystyle {\mathbf {x} }_{1},\dots ,{\mathbf {x} }_{n}}
p
×
1
{\displaystyle p\times 1}
x
¯
=
(
x
1
+
⋯
+
x
n
)
/
n
{\displaystyle {\overline {\mathbf {x} }}=(\mathbf {x} _{1}+\cdots +\mathbf {x} _{n})/n}
sei der Mittelwert. Die positiv definite
p
×
p
{\displaystyle p\times p}
W
=
∑
i
=
1
n
(
x
i
−
x
¯
)
(
x
i
−
x
¯
)
′
/
(
n
−
1
)
{\displaystyle {\mathbf {W} }=\sum _{i=1}^{n}(\mathbf {x} _{i}-{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})'/(n-1)}
sei ihre Stichproben-Kovarianzmatrix . (Die Transponierte einer Matrix
M
{\displaystyle M}
M
′
{\displaystyle M'}
μ
{\displaystyle \mu }
p
×
1
{\displaystyle p\times 1}
T -Quadrat-Verteilung
t
2
=
n
(
x
¯
−
μ
)
′
W
−
1
(
x
¯
−
μ
)
.
{\displaystyle t^{2}=n({\overline {\mathbf {x} }}-{\mathbf {\mu } })'{\mathbf {W} }^{-1}({\overline {\mathbf {x} }}-{\mathbf {\mu } }).}
t
2
{\displaystyle t^{2}}
Mahalanobis-Abstand .
Insbesondere kann gezeigt werden[3]
x
1
,
…
,
x
n
∼
N
p
(
μ
,
V
)
{\displaystyle {\mathbf {x} }_{1},\dots ,{\mathbf {x} }_{n}\sim N_{p}(\mu ,{\mathbf {V} })}
x
¯
{\displaystyle {\overline {\mathbf {x} }}}
W
{\displaystyle {\mathbf {W} }}
W
{\displaystyle {\mathbf {W} }}
n
−
1
{\displaystyle n-1}
Freiheitsgraden , so dass
W
∼
W
p
(
V
,
n
−
1
)
{\displaystyle \mathbf {W} \sim W_{p}(V,n-1)}
und ist unabhängig von
x
¯
{\displaystyle {\overline {\mathbf {x} }}}
x
¯
∼
N
p
(
μ
,
V
/
n
)
{\displaystyle {\overline {\mathbf {x} }}\sim {\mathcal {N}}_{p}(\mu ,V/n)}
Daraus folgt
t
2
=
n
(
x
¯
−
μ
)
′
W
−
1
(
x
¯
−
μ
)
∼
T
2
(
p
,
n
−
1
)
.
{\displaystyle t^{2}=n({\overline {\mathbf {x} }}-{\mathbf {\mu } })'{\mathbf {W} }^{-1}({\overline {\mathbf {x} }}-{\mathbf {\mu } })\sim T^{2}(p,n-1).}
↑ Hotelling's T². International Statistical Institute . abgerufen am 25. September 2020 (englisch). ↑ H. Hotelling (1931). The generalization of Student’s ratio, Ann. Math. Statist., 2 (3), S. 360–378, doi :10.1214/aoms/1177732979 JSTOR :2957535 .
↑ K.V. Mardia, J.T. Kent, and J.M. Bibby (1979) Multivariate Analysis , Academic Press, ISBN 0-12-471250-9 .
Diskrete univariate Verteilungen
Kontinuierliche univariate Verteilungen
Multivariate Verteilungen