Matrix (Mathematik)

Schema für eine allgemeine $m\times n$-Matrix

Bezeichnungen

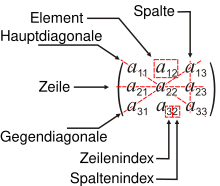
In der Mathematik versteht man unter einer Matrix (Plural Matrizen) eine rechteckige Anordnung (Tabelle) von Elementen (meist mathematischer Objekte, etwa Zahlen). Rechteckig bedeutet, dass die Anordnung der Elemente stattfindet in Zeilen und Spalten. Das Element einer Matrix $A$ in der $i$-ten Zeile und $j$-ten Spalte wird mit $a_{ij}$ bezeichnet. Mit den Objekten einer Matrix lässt sich dann in bestimmter Weise rechnen, indem man Matrizen zum Beispiel addiert oder miteinander multipliziert.

Matrizen sind ein Schlüsselkonzept der linearen Algebra und tauchen in fast allen Gebieten der Mathematik auf. Sie stellen Zusammenhänge, in denen Linearkombinationen eine Rolle spielen, übersichtlich dar und erleichtern damit Rechen- und Gedankenvorgänge. Sie werden insbesondere dazu benutzt, lineare Abbildungen darzustellen und lineare Gleichungssysteme zu beschreiben und zu lösen.

Der Name „Matrix“ (lateinisch für „Muttertier“, „Gebärmutter“, abgeleitet von mater – Mutter) wurde 1850 von James Joseph Sylvester geprägt.

Eine Anordnung, wie in nebenstehender Abbildung, von $m\cdot n$ Elementen $a_{ij}$ erfolgt in $m$ Zeilen und $n$ Spalten. Die Verallgemeinerung auf mehr als zwei Indizes wird auch Hypermatrix genannt.

Begriffe und erste Eigenschaften

Notation

Als Notation hat sich die Anordnung der Elemente in Zeilen und Spalten zwischen zwei großen öffnenden und schließenden Klammern durchgesetzt. In der Regel verwendet man runde Klammern, es werden aber auch eckige verwendet. Zum Beispiel bezeichnen

${\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{pmatrix}}$ und ${\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix}}$

Matrizen mit zwei Zeilen und drei Spalten. Matrizen werden üblicherweise mit Großbuchstaben (manchmal fett gedruckt oder, handschriftlich, einfach oder doppelt unterstrichen), vorzugsweise $A$, bezeichnet. Eine Matrix mit m Zeilen und n Spalten nennt man eine Matrix vom Typ (m,n) oder kurz (m,n)-Matrix. Auch mxn-Matrix oder m x n-Matrix sind verbreitet. Man schreibt sie

$A={\boldsymbol {A}}={\underline {A}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &&\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}=(a_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$.

Elemente der Matrix

Ein $a_{ij}$ nennt man Matrixelement oder kurz Element, neuerdings auch Matrixeintrag oder kurz Eintrag. Auch Matrixkomponente oder kurz Komponente werden verwendet. Insbesondere im Fall von (m,1)- oder (1,n)-Matrizen ist der Name Komponente verbreitet. Die Elemente können sowohl reelle als auch komplexe Zahlen sein, aber auch andere mathematische Objekte, z. B. Vektoren, Polynome, Differentiale, andere Formeln oder selbst wieder Matrizen.

Ein bestimmtes Element beschreibt man durch zwei Indizes, meist ist das Element in der ersten Zeile und der ersten Spalte durch $a_{11}$ beschrieben. Allgemein bezeichnet $a_{ij}$ das Element in der $i$-ten Zeile und der $j$-ten Spalte. Bei der Indizierung wird dabei stets als erstes der Zeilenindex und als zweites der Spaltenindex des Elements genannt. Merkregel: Zeile zuerst, Spalte später. Wenn Verwechslungsgefahr besteht, werden die beiden Indizes mit einem Komma abgetrennt. So wird zum Beispiel das Matrixelement in der ersten Zeile und der elften Spalte mit $a_{1,11}$ bezeichnet.

Einzelne Zeilen und Spalten werden oft als Spalten- oder Zeilenvektoren bezeichnet. Ein Beispiel:

$A={\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}},$ hier sind ${\begin{pmatrix}a_{11}\\a_{21}\end{pmatrix}}$ und ${\begin{pmatrix}a_{12}\\a_{22}\end{pmatrix}}$ die Spalten oder Spaltenvektoren sowie ${\begin{pmatrix}a_{11}&a_{12}\end{pmatrix}}$ und ${\begin{pmatrix}a_{21}&a_{22}\end{pmatrix}}$ die Zeilen oder Zeilenvektoren.

Bei einzeln stehenden Zeilen- und Spaltenvektoren einer Matrix wird gelegentlich der unveränderliche Index weggelassen. Manchmal werden Spaltenvektoren zur kompakteren Darstellung als transponierte Zeilenvektoren geschrieben, also:

${\begin{pmatrix}a_{11}\\a_{21}\end{pmatrix}}$ oder ${\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}$ als ${\begin{pmatrix}a_{11}&a_{21}\end{pmatrix}}^{T}$ oder ${\begin{pmatrix}a_{1}&a_{2}\end{pmatrix}}^{T}$

Typ

Der Typ einer Matrix ergibt sich aus der Anzahl ihrer Zeilen und Spalten. Eine Matrix mit $m$ Zeilen und $n$ Spalten nennt man eine $m\times n$-Matrix (sprich: m-mal-n- oder m-Kreuz-n-Matrix). Stimmen Zeilen- und Spaltenanzahl überein, so spricht man von einer quadratischen Matrix.

Eine Matrix, die aus nur einer Spalte oder nur einer Zeile besteht, wird üblicherweise als Vektor aufgefasst. Einen Vektor mit $n$ Elementen kann man je nach Kontext als einspaltige $n\times 1$-Matrix oder einzeilige $1\times n$-Matrix darstellen. Neben den Begriffen Spaltenvektor und Zeilenvektor sind hierfür die Begriffe Spaltenmatrix und Zeilenmatrix geläufig. Eine $1\times 1$-Matrix ist sowohl Spalten- als auch Zeilenmatrix und wird als Skalar angesehen.

Formale Darstellung

Eine Matrix ist eine doppelt indizierte Familie. Formal ist dies eine Funktion

$A\colon \{1,\dotsc ,m\}\times \{1,\dotsc ,n\}\to K,\quad (i,j)\mapsto a_{ij},$

die jedem Indexpaar $(i,j)$ als Funktionswert das Element $a_{ij}$ zuordnet. Beispielsweise wird dem Indexpaar $(1,2)$ als Funktionswert das Element $a_{12}$ zugeordnet. Der Funktionswert $a_{ij}$ ist also das Element in der $i$-ten Zeile und der $j$-ten Spalte. Die Variablen $m$ und $n$ entsprechen der Anzahl der Zeilen bzw. Spalten. Nicht zu verwechseln mit dieser formalen Definition einer Matrix als Funktion ist, dass Matrizen selbst lineare Abbildungen beschreiben.

Die Menge $\operatorname {Abb} \left(\{1,\dotsc ,m\}\times \{1,\dotsc ,n\},K\right)$ aller $m\times n$-Matrizen über der Menge $K$ wird in üblicher mathematischer Notation auch $K^{\{1,\dotsc ,m\}\times \{1,\dotsc ,n\}}$ geschrieben; hierfür hat sich die Kurznotation $K^{m\times n}$ eingebürgert. Manchmal werden die Schreibweisen $K^{m,n},$ $M(m\times n,K)$ oder seltener ${}^{m}K^{n}$ benutzt.

Addition und Multiplikation

Auf dem Raum der Matrizen werden elementare Rechenoperationen definiert.

Matrizenaddition

→ Hauptartikel: Matrizenaddition

Zwei Matrizen können addiert werden, wenn sie vom selben Typ sind, das heißt, wenn sie dieselbe Anzahl von Zeilen und dieselbe Anzahl von Spalten besitzen. Die Summe zweier $m\times n$-Matrizen ist komponentenweise definiert:

$A+B:=(a_{ij}+b_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$

Rechenbeispiel:

$\left({\begin{array}{r}1&-3&2\\1&2&7\end{array}}\right)+\left({\begin{array}{r}0&3&5\\2&1&-1\end{array}}\right)=\left({\begin{array}{r}1+0&-3+3&2+5\\1+2&2+1&7+(-1)\end{array}}\right)={\begin{pmatrix}1&0&7\\3&3&6\end{pmatrix}}$

In der linearen Algebra sind die Matrixelemente üblicherweise Elemente eines Körpers (Körperelemente), wie der reellen oder komplexen Zahlen. In diesem Fall ist die Matrizenaddition assoziativ, kommutativ und besitzt mit der Nullmatrix ein neutrales Element. Im Allgemeinen besitzt die Matrizenaddition diese Eigenschaften jedoch nur, wenn die Matrixelemente Körperelemente einer algebraischen Struktur sind, die diese Eigenschaften hat.

Skalarmultiplikation

→ Hauptartikel: Skalarmultiplikation

Eine Matrix wird mit einem Skalar multipliziert, indem jedes Element der Matrix mit dem Skalar multipliziert wird:

$c\cdot A:=(c\cdot a_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$

Rechenbeispiel:

$5\cdot \left({\begin{array}{r}1&-3&2\\1&2&7\end{array}}\right)={\begin{pmatrix}5\cdot 1&5\cdot (-3)&5\cdot 2\\5\cdot 1&5\cdot 2&5\cdot 7\end{pmatrix}}=\left({\begin{array}{r}5&-15&10\\5&10&35\end{array}}\right)$

Die Skalarmultiplikation darf nicht mit dem Skalarprodukt verwechselt werden. Um die Skalarmultiplikation durchführen zu dürfen, müssen der Skalar $c$ und die Matrixelemente demselben Ring $(K,+,\cdot ,0)$ entstammen. Die Menge der $m\times n$-Matrizen ist in diesem Fall ein (Links-)Modul über $K.$

Matrizenmultiplikation

→ Hauptartikel: Matrizenmultiplikation

Zwei Matrizen können multipliziert werden, wenn die Spaltenanzahl der linken mit der Zeilenanzahl der rechten Matrix übereinstimmt. Das Produkt einer $l\times m$-Matrix $A=(a_{ij})_{i=1,\dotsc ,l,\;j=1,\dotsc ,m}$ und einer $m\times n$-Matrix $B=(b_{ij})_{i=1,\dotsc ,m,\;j=1,\dotsc ,n}$ ist eine $l\times n$-Matrix $C=(c_{ij})_{i=1,\dotsc ,l,\;j=1,\dotsc ,n},$ deren Elemente berechnet werden, indem die Produktsummenformel, ähnlich dem Skalarprodukt, auf Paare aus einem Zeilenvektor der ersten und einem Spaltenvektor der zweiten Matrix angewandt wird:

$c_{ij}=\sum _{k=1}^{m}a_{ik}\cdot b_{kj}$

Die Matrizenmultiplikation ist nicht kommutativ, d. h., im Allgemeinen gilt $B\cdot A\neq A\cdot B$. Die Matrizenmultiplikation ist allerdings assoziativ, d. h., es gilt stets:

$(A\cdot B)\cdot C=A\cdot (B\cdot C)$

Eine Kette von Matrix-Multiplikationen kann daher unterschiedlich geklammert werden. Das Problem, eine Klammerung zu finden, die zu einer Berechnung mit der minimalen Anzahl von elementaren arithmetischen Operationen führt, ist ein Optimierungsproblem. Die Matrizenaddition und Matrizenmultiplikation genügen zudem den beiden Distributivgesetzen:

$(A+B)\cdot C=A\cdot C+B\cdot C$

für alle $l\times m$-Matrizen $A,B$ und $m\times n$-Matrizen $C$ sowie

$A\cdot (B+C)=A\cdot B+A\cdot C$

für alle $l\times m$-Matrizen $A$ und $m\times n$-Matrizen $B,C.$

Quadratische Matrizen $A\in K^{n\times n}$ können mit sich selbst multipliziert werden, analog zur Potenz bei den reellen Zahlen führt man abkürzend die Matrixpotenz $A^{2}=A\cdot A$ oder $A^{3}=A\cdot A\cdot A$ ein. Damit ist es auch sinnvoll, quadratische Matrizen als Elemente in Polynome einzusetzen. Zu weitergehenden Ausführungen hierzu siehe unter Charakteristisches Polynom. Zur einfacheren Berechnung kann hier die jordansche Normalform verwendet werden. Quadratische Matrizen über $\mathbb {R}$ oder $\mathbb {C}$ kann man darüber hinaus sogar in Potenzreihen einsetzen, vgl. Matrixexponential. Eine besondere Rolle bezüglich der Matrizenmultiplikation spielen die quadratischen Matrizen über einem Ring $R$, also $R^{n\times n}$. Diese bilden selbst mit der Matrizenaddition und -multiplikation wiederum einen Ring, der Matrizenring genannt wird.

Weitere Rechenoperationen

Transponierte Matrix

→ Hauptartikel: Transponierte Matrix

Animation zur Transponierung der Matrix A

Die Transponierte einer $m\times n$-Matrix $A=\left(a_{ij}\right)$ ist die $n\times m$-Matrix $A^{T}=\left(a_{ji}\right)$, das heißt, zu

$A={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &&\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}$

ist

$A^{T}={\begin{pmatrix}a_{11}&\dots &a_{m1}\\\vdots &&\vdots \\a_{1n}&\dots &a_{mn}\end{pmatrix}}$

die Transponierte. Man schreibt also die erste Zeile als erste Spalte, die zweite Zeile als zweite Spalte usw. Die Matrix wird an ihrer Hauptdiagonalen $a_{11},a_{22},\dotsc$ gespiegelt. Es gelten die folgenden Rechenregeln:

${\begin{aligned}(A+B)^{T}&=A^{T}+B^{T}\\(c\cdot A)^{T}&=c\cdot A^{T}\\\left(A^{T}\right)^{T}&=A\\(A\cdot B)^{T}&=B^{T}\cdot A^{T}\\\left(A^{-1}\right)^{T}&=\left(A^{T}\right)^{-1}\end{aligned}}$

Bei Matrizen über $\mathbb {R}$ ist die adjungierte Matrix genau die transponierte Matrix.

Inverse Matrix

→ Hauptartikel: Inverse Matrix

Falls die Determinante einer quadratischen $n\times n$-Matrix $A$ über einem Körper $K$ nicht gleich null ist, d. h., falls $\det(A)\neq 0$, so existiert die zur Matrix $A$ inverse Matrix $A^{-1}$. Für diese gilt

$AA^{-1}=A^{-1}A=E$,

wobei $E$ die $n\times n$-Einheitsmatrix ist. Matrizen, die eine inverse Matrix besitzen, bezeichnet man als invertierbare oder reguläre Matrizen. Diese haben vollen Rang. Umgekehrt werden nichtinvertierbare Matrizen als singuläre Matrizen bezeichnet. Eine Verallgemeinerung der Inversen für singuläre Matrizen sind sog. pseudoinverse Matrizen.

Vektor-Vektor-Produkte

Das Matrixprodukt $v\cdot w$ zweier $n\times 1$-Vektoren $v$ und $w$ ist nicht definiert, da die Anzahl $1$ der Spalten von $v$ im Allgemeinen ungleich der Anzahl $n$ der Zeilen von $w$ ist. Die beiden Produkte $v^{T}\cdot w$ und $v\cdot w^{T}$ existieren jedoch.

Das erste Produkt $v^{T}\cdot w$ ist eine $1\times 1$-Matrix, die als Zahl interpretiert wird; sie wird das Standardskalarprodukt von $v$ und $w$ genannt und mit $\langle v,w\rangle$ oder ${\vec {v}}\cdot {\vec {w}}$ bezeichnet. Geometrisch entspricht dieses Skalarprodukt in einem kartesischen Koordinatensystem dem Produkt

${\vec {v}}\cdot {\vec {w}}=|{\vec {v}}|\cdot |{\vec {w}}|\cdot \cos \sphericalangle ({\vec {v}},{\vec {w}})$

der Beträge der beiden Vektoren und des Kosinus des von den beiden Vektoren eingeschlossenen Winkels. Beispielsweise gilt

${\begin{pmatrix}1\\2\\3\end{pmatrix}}^{T}\cdot \left({\begin{array}{r}-2\\-1\\1\end{array}}\right)={\begin{pmatrix}1&2&3\end{pmatrix}}\cdot \left({\begin{array}{r}-2\\-1\\1\end{array}}\right)=1\cdot (-2)+2\cdot (-1)+3\cdot 1=-1$

Das zweite Produkt $v\cdot w^{T}$ ist eine $n\times n$-Matrix und heißt dyadisches Produkt oder Tensorprodukt von $v$ und $w$ (geschrieben $v\otimes w$). Seine Spalten sind skalare Vielfache von $v$, seine Zeilen skalare Vielfache von $w^{T}$. Beispielsweise gilt

${\begin{pmatrix}1\\2\\3\end{pmatrix}}\cdot \left({\begin{array}{r}-2\\-1\\1\end{array}}\right)^{T}={\begin{pmatrix}1\\2\\3\end{pmatrix}}\cdot {\begin{pmatrix}-2&-1&1\end{pmatrix}}={\begin{pmatrix}1\cdot (-2)&1\cdot (-1)&1\cdot 1\\2\cdot (-2)&2\cdot (-1)&2\cdot 1\\3\cdot (-2)&3\cdot (-1)&3\cdot 1\end{pmatrix}}={\begin{pmatrix}-2&-1&1\\-4&-2&2\\-6&-3&3\end{pmatrix}}.$

Vektorräume von Matrizen

→ Hauptartikel: Matrizenraum

Die Menge der $m\times n$-Matrizen über einem Körper $K$ bildet mit der Matrizenaddition und der Skalarmultiplikation einen $K$-Vektorraum. Dieser Vektorraum $K^{m\times n}$ hat die Dimension $m\cdot n$. Eine Basis von $K^{m\times n}$ ist gegeben durch die Menge der Standardmatrizen $E_{ij}$ mit $i\in \{1,\dotsc ,m\}$, $j\in \{1,\dotsc ,n\}$. Diese Basis wird manchmal als Standardbasis von $K^{m\times n}$ bezeichnet.

Die Spur des Matrixprodukts $A^{T}\cdot B$

$\left\langle A,B\right\rangle =\operatorname {spur} (A^{T}B)=\sum _{j=1}^{n}\sum _{i=1}^{m}a_{ij}b_{ij}$

ist dann im Spezialfall $K=\mathbb {R}$ ein reelles Skalarprodukt. In diesem euklidischen Vektorraum stehen die symmetrischen Matrizen und die schiefsymmetrischen Matrizen senkrecht aufeinander. Ist $A$ eine symmetrische und $B$ eine schiefsymmetrische Matrix, so gilt ${\begin{matrix}\left\langle A,B\right\rangle =0\end{matrix}}$.

Im Spezialfall $K=\mathbb {C}$ ist die Spur des Matrixproduktes ${\overline {A^{T}}}\cdot B$

$\left\langle A,B\right\rangle =\operatorname {spur} ({\overline {A^{T}}}B)=\sum _{j=1}^{n}\sum _{i=1}^{m}{\overline {a_{ij}}}b_{ij}$

ein komplexes Skalarprodukt und der Matrizenraum wird zu einem unitären Vektorraum. Dieses Skalarprodukt wird Frobenius-Skalarprodukt genannt. Die von dem Frobenius-Skalarprodukt induzierte Norm heißt Frobeniusnorm und mit ihr wird der Matrizenraum zu einem Banachraum.

Anwendungen

Zusammenhang mit linearen Abbildungen

Das Besondere an Matrizen über einem Ring $K$ ist der Zusammenhang zu linearen Abbildungen. Zu jeder Matrix $A\in K^{m\times n}$ lässt sich eine lineare Abbildung mit Definitionsbereich $K^{n}$ (Menge der Spaltenvektoren) und Wertebereich $K^{m}$ definieren, indem man jeden Spaltenvektor $u\in K^{n}$ auf $A\cdot u\in K^{m}$ abbildet. Umgekehrt entspricht jeder linearen Abbildung $f\colon K^{n}\to K^{m}$ auf diese Weise genau eine $m\times n$-Matrix $A$; dabei sind die Spalten von $A$ die Bilder der Standard-Basisvektoren $e_{1},\dotsc ,e_{n}$ von $K^{n}$ unter $f$. Diesen Zusammenhang zwischen linearen Abbildungen und Matrizen bezeichnet man auch als (kanonischen) Isomorphismus

$\operatorname {Hom} _{K}(K^{n},K^{m})\simeq K^{m\times n}.$

Er stellt bei vorgegebenem $K,$ $m$ und $n$ eine Bijektion zwischen der Menge der Matrizen und der Menge der linearen Abbildungen dar. Das Matrixprodukt geht hierbei über in die Komposition (Hintereinanderausführung) linearer Abbildungen. Weil die Klammerung bei der Hintereinanderausführung dreier linearer Abbildungen keine Rolle spielt, gilt dies für die Matrixmultiplikation, diese ist also assoziativ.

Ist $K$ sogar ein Körper, kann man statt der Spaltenvektorräume beliebige endlichdimensionale $K$-Vektorräume $V$ und $W$ (der Dimension $n$ bzw. $m$) betrachten. (Falls $K$ ein kommutativer Ring mit 1 ist, dann kann man analog freie K-Moduln betrachten.) Diese sind nach Wahl von Basen $v=(v_{1},\dotsc ,v_{n})$ von $V$ und $w=(w_{1},\dotsc ,w_{m})$ von $W$ zu den Koordinatenräumen $K^{n}$ bzw. $K^{m}$ isomorph, weil zu einem beliebigen Vektor $u\in V$ eine eindeutige Zerlegung in Basisvektoren

$u=\sum _{j=1}^{n}\alpha _{j}v_{j}$

existiert und die darin vorkommenden Körperelemente $\alpha _{j}$ den Koordinatenvektor

${}_{v}u={\begin{pmatrix}\alpha _{1}\\\vdots \\\alpha _{n}\end{pmatrix}}\in K^{n}$

bilden. Jedoch hängt der Koordinatenvektor von der verwendeten Basis $v$ ab, die daher in der Bezeichnung ${}_{v}u$ vorkommt.

Analog verhält es sich im Vektorraum $W.$ Ist eine lineare Abbildung $f\colon V\to W$ gegeben, so lassen sich die Bilder der Basisvektoren von $V$ eindeutig in die Basisvektoren von $W$ zerlegen in der Form

$f(v_{j})=\sum _{i=1}^{m}a_{ij}w_{i}$

mit Koordinatenvektor

${}_{w}f(v_{j})={\begin{pmatrix}a_{1j}\\\vdots \\a_{mj}\end{pmatrix}}\in K^{m}.$

Die Abbildung ist dann vollständig festgelegt durch die sog. Abbildungsmatrix

${}_{w}f_{v}={\begin{pmatrix}a_{11}&\ldots &a_{1n}\\\vdots &&\vdots \\a_{m1}&\ldots &a_{mn}\end{pmatrix}}\in K^{m\times n},$

denn für das Bild des o. g. Vektors $u$ gilt

$f(u)=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}\alpha _{j}w_{i},$

also ${}_{w}f(u)={}_{w}f_{v}\cdot {}_{v}u$ („Koordinatenvektor = Matrix mal Koordinatenvektor“). (Die Matrix ${}_{w}f_{v}$ hängt von den verwendeten Basen $v$ und $w$ ab; bei der Multiplikation wird die Basis $v$, die links und rechts vom Malpunkt steht, „weggekürzt“, und die „außen“ stehende Basis $w$ bleibt übrig.)

Die Hintereinanderausführung zweier linearer Abbildungen $f\colon V\to W$ und $g\colon W\to X$ (mit Basen $v$, $w$ bzw. $x$) entspricht dabei der Matrixmultiplikation, also

${}_{x}(g\circ f)_{v}={}_{x}g_{w}\cdot {}_{w}f_{v}$

(auch hier wird die Basis $w$ „weggekürzt“).

Somit ist die Menge der linearen Abbildungen von $V$ nach $W$ wieder isomorph zu $K^{m\times n}.$ Der Isomorphismus $f\mapsto {}_{w}f_{v}$ hängt aber von den gewählten Basen $v$ und $w$ ab und ist daher nicht kanonisch: Bei Wahl einer anderen Basis $v'$ für $V$ bzw. $w'$ für $W$ wird derselben linearen Abbildung nämlich eine andere Matrix zugeordnet, die aus der alten durch Multiplikation von rechts bzw. links mit einer nur von den beteiligten Basen abhängigen invertierbaren $m\times m$- bzw. $n\times n$-Matrix (sog. Basiswechselmatrix) entsteht. Das folgt durch zweimalige Anwendung der Multiplikationsregel aus dem vorigen Absatz, nämlich

${}_{w'}f_{v'}={}_{w'}e_{w}^{W}\cdot {}_{w}f_{v}\cdot {}_{v}e_{v'}^{V}$

(„Matrix = Basiswechselmatrix mal Matrix mal Basiswechselmatrix“). Dabei bilden die Identitätsabbildungen $e^{V}$ und $e^{W}$ jeden Vektor aus $V$ bzw. $W$ auf sich selbst ab.

Bleibt eine Eigenschaft von Matrizen unberührt von solchen Basiswechseln, so ist es sinnvoll, diese Eigenschaft basisunabhängig der entsprechenden linearen Abbildung zuzusprechen.

Im Zusammenhang mit Matrizen oft auftretende Begriffe sind der Rang und die Determinante einer Matrix. Der Rang ist (falls $K$ ein Körper ist) im angeführten Sinne basisunabhängig, und man kann somit vom Rang auch bei linearen Abbildungen sprechen. Die Determinante ist nur für quadratische Matrizen definiert, die dem Fall $V=W$ entsprechen; sie bleibt unverändert, wenn derselbe Basiswechsel im Definitions- und Wertebereich durchgeführt wird, wobei beide Basiswechselmatrizen zueinander invers sind:

${}_{v'}f_{v'}=({}_{v}e_{v'}^{V})^{-1}\cdot {}_{v}f_{v}\cdot {}_{v}e_{v'}^{V}$

In diesem Sinne ist also die Determinante basisunabhängig.

Umformen von Matrizengleichungen

Speziell in den multivariaten Verfahren werden häufig Beweisführungen, Herleitungen usw. im Matrizenkalkül durchgeführt.

Gleichungen werden im Prinzip wie algebraische Gleichungen umgeformt, wobei jedoch die Nichtkommutativität der Matrixmultiplikation sowie die Existenz von Nullteilern beachtet werden muss.

Beispiel: Lineares Gleichungssystem als einfache Umformung

Gesucht ist der Lösungsvektor $x$ eines linearen Gleichungssystems

$A\cdot x=b$

mit $A$ als $n\times n$-Koeffizientenmatrix. Wenn die inverse Matrix $A^{-1}$ existiert, kann man mit ihr von links multiplizieren:

$A^{-1}\cdot A\cdot x=A^{-1}\cdot b\Leftrightarrow E\cdot x=A^{-1}\cdot b$

und man erhält als Lösung

$x=A^{-1}\cdot b.$

Spezielle Matrizen

Eigenschaften von Endomorphismen

Die folgenden Eigenschaften quadratischer Matrizen entsprechen Eigenschaften von Endomorphismen, die durch sie dargestellt werden.

Orthogonale Matrizen

Eine reelle Matrix $A$ ist orthogonal, wenn die zugehörige lineare Abbildung das Standardskalarprodukt erhält, das heißt, wenn

$\langle Av,Aw\rangle =\langle v,w\rangle$

gilt. Diese Bedingung ist äquivalent dazu, dass $A$ die Gleichung

$A^{-1}=A^{T}$

bzw.

$A\,A^{T}=E$

erfüllt. Diese Matrizen stellen Spiegelungen, Drehungen und Drehspiegelungen dar.

Unitäre Matrizen

Sie sind das komplexe Gegenstück zu den orthogonalen Matrizen. Eine komplexe Matrix $A$ ist unitär, wenn die zugehörige Transformation die Normierung erhält, das heißt, wenn

$\langle Av,Aw\rangle =\langle v,w\rangle$

gilt. Diese Bedingung ist äquivalent dazu, dass $A$ die Gleichung

$A^{-1}=A^{*}$

erfüllt; dabei bezeichnet $A^{*}$ die konjugiert-transponierte Matrix zu $A.$ Fasst man den $n$-dimensionalen komplexen Vektorraum als $2n$-dimensionalen reellen Vektorraum auf, so entsprechen die unitären Matrizen genau denjenigen orthogonalen Matrizen, die mit der Multiplikation mit $\mathrm {i}$ vertauschen.

Projektionsmatrizen

Eine Matrix ist eine Projektionsmatrix, falls

$A=A^{2}$

gilt, sie also idempotent ist: Das heißt, die mehrfache Anwendung einer Projektionsmatrix auf einen Vektor lässt das Resultat unverändert. Eine idempotente Matrix hat keinen vollen Rang, es sei denn, sie ist die Einheitsmatrix. Geometrisch entsprechen Projektionsmatrizen der Parallelprojektion entlang des Nullraumes der Matrix. Steht der Nullraum senkrecht auf dem Bildraum, so erhält man eine Orthogonalprojektion.
Beispiel: Es sei $X$ eine $(m\times n)$-Matrix und damit selbst nicht invertierbar. Falls der Rang von $X$ gleich $n$ ist, dann ist $(X^{T}X)$ invertierbar und die $(m\times m)$-Matrix

$A=X\,(X^{T}X)^{-1}X^{T}$

idempotent. Diese Matrix wird beispielsweise in der Methode der kleinsten Quadrate verwendet.

Nilpotente Matrizen

Eine Matrix $N$ heißt nilpotent, falls eine Potenz $N^{k}$ (und damit auch jede höhere Potenz) die Nullmatrix ergibt.

Eigenschaften von Bilinearformen

Im Folgenden sind Eigenschaften von Matrizen aufgelistet, die Eigenschaften der zugehörigen Bilinearform

$(v,w)\mapsto v^{T}Aw$

entsprechen. Trotzdem können diese Eigenschaften für die dargestellten Endomorphismen eine eigenständige Bedeutung besitzen.

Symmetrische Matrizen

Eine Matrix $A$ heißt symmetrisch, wenn sie gleich ihrer transponierten Matrix ist:

$A^{T}=A$

Anschaulich gesprochen sind die Elemente symmetrischer Matrizen symmetrisch zur Hauptdiagonalen. Beispiel:

${\begin{pmatrix}1&2&3\\2&4&5\\3&5&6\end{pmatrix}}^{T}={\begin{pmatrix}1&2&3\\2&4&5\\3&5&6\end{pmatrix}}$

Symmetrische Matrizen entsprechen einerseits symmetrischen Bilinearformen:

$v^{T}Aw=w^{T}Av,$

andererseits den selbstadjungierten linearen Abbildungen:

$\langle Av,w\rangle =\langle v,Aw\rangle$

Hermitesche Matrizen

Hermitesche Matrizen sind das komplexe Analogon der symmetrischen Matrizen. Sie entsprechen den hermiteschen Sesquilinearformen und den selbstadjungierten Endomorphismen.
Eine Matrix $A\in \mathbb {C} ^{n\times n}$ ist hermitesch oder selbstadjungiert, wenn gilt:

$A=A^{*}$

Schiefsymmetrische Matrizen

Eine Matrix $A$ heißt schiefsymmetrisch oder antisymmetrisch, wenn gilt:

$-A^{T}=A$

Um diese Bedingung zu erfüllen, müssen alle Elemente der Hauptdiagonale den Wert Null haben; die restlichen Werte werden an der Hauptdiagonale gespiegelt und mit $-1$ multipliziert.
Beispiel:

$\left({\begin{array}{r}0&1&2\\-1&0&3\\-2&-3&0\end{array}}\right)$

Schiefsymmetrische Matrizen entsprechen antisymmetrischen Bilinearformen:

$v^{T}\cdot A\cdot w=-w^{T}\cdot A\cdot v$

und antiselbstadjungierten Endomorphismen:

$\langle Av,w\rangle =-\langle v,Aw\rangle$

Positiv definite Matrizen

Eine reelle Matrix ist positiv definit, wenn die zugehörige Bilinearform positiv definit ist, das heißt, wenn für alle Vektoren $v\neq 0$ gilt:

$v^{T}\cdot A\cdot v>0$

Positiv definite Matrizen definieren verallgemeinerte Skalarprodukte. Hat die Bilinearform keine negativen Werte, heißt die Matrix positiv semidefinit. Analog kann eine Matrix negativ definit beziehungsweise negativ semidefinit heißen, wenn die obige Bilinearform nur negative beziehungsweise keine positiven Werte hat. Matrizen, die keine dieser Eigenschaften erfüllen, heißen indefinit.

Weitere Konstruktionen

Konjugierte und adjungierte Matrix

Enthält eine Matrix komplexe Zahlen, erhält man die konjugierte Matrix, indem man ihre Komponenten durch die konjugiert komplexen Elemente ersetzt. Die adjungierte Matrix (auch hermitesch konjugierte Matrix) einer Matrix $A$ wird mit $A^{*}$ bezeichnet und entspricht der transponierten Matrix, bei der zusätzlich alle Elemente komplex konjugiert werden.

Adjunkte oder komplementäre Matrix

Die komplementäre Matrix $\operatorname {adj} (A)$ einer quadratischen Matrix $A$ setzt sich aus deren Unterdeterminanten zusammen, wobei eine Unterdeterminante Minor genannt wird. Für die Ermittlung der Unterdeterminanten $\det(A_{ij})$ werden die $i$-te Zeile und $j$-te Spalte von $A$ gestrichen. Aus der resultierenden $(n-1)\times (n-1)$-Matrix wird dann die Determinante $\det(A_{ij})$ berechnet. Die komplementäre Matrix hat dann die Elemente $(-1)^{i+j}\det(A_{ji}).$ Diese Matrix wird manchmal auch als Matrix der Kofaktoren bezeichnet.
Man verwendet die komplementäre Matrix beispielsweise zur Berechnung der Inversen einer Matrix $A$, denn nach dem Laplaceschen Entwicklungssatz gilt:

$\operatorname {adj} (A)\cdot A=A\cdot \operatorname {adj} (A)=\det(A)\cdot E_{n}$

Damit ist die Inverse $A^{-1}={\frac {1}{\det(A)}}\cdot \operatorname {adj} (A),$ wenn $\det(A)\neq 0.$

Übergangs- oder stochastische Matrizen

Eine Übergangs- oder stochastische Matrix ist eine Matrix, deren Elemente alle zwischen 0 und 1 liegen und deren Zeilen bzw. Spaltensummen 1 ergeben. Sie dienen in der Stochastik zur Charakterisierung zeitlich diskreter Markow-Ketten mit endlichem Zustandsraum. Ein Spezialfall hiervon sind die doppelt-stochastischen Matrizen.

Unendlichdimensionale Räume

Für unendlichdimensionale Vektorräume (sogar über Schiefkörpern) gilt, dass jede lineare Abbildung $f\colon U\to V$ eindeutig durch die Bilder $f(u)$ der Elemente $u$ einer Basis ${\mathcal {B}}_{U}\subset U$ bestimmt ist und diese beliebig gewählt werden und zu einer linearen Abbildung auf ganz $U$ fortgesetzt werden können. Ist nun ${\mathcal {B}}_{V}$ eine Basis von $V$, so lässt sich $f(u)$ eindeutig als (endliche) Linearkombination von Basisvektoren schreiben, d. h., es existieren eindeutige Koeffizienten $f(u)_{b}\in K$ für $b\in {\mathcal {B}}_{V}$, von denen nur endlich viele von null verschieden sind, sodass $f(u)=\sum _{b\in {\mathcal {B}}_{V}}f(u)_{b}b$. Dementsprechend lässt sich jede lineare Abbildung als möglicherweise unendliche Matrix auffassen, wobei jedoch in jeder Spalte (${\mathcal {B}}_{U}$ „nummeriere“ die Spalten und die Spalte zu $u$ bestehe dann aus den von den Elementen von ${\mathcal {B}}_{V}$ nummerierten Koordinaten $f(u)_{b}$) nur endlich viele Elemente von null verschieden sind, und umgekehrt. Die entsprechend definierte Matrixmultiplikation entspricht wiederum der Komposition linearer Abbildungen.

In der Funktionalanalysis betrachtet man topologische Vektorräume, d. h. Vektorräume, auf denen man von Konvergenz sprechen und dementsprechend unendliche Summen bilden kann. Auf solchen können Matrizen mit unendlich vielen von null verschiedenen Elementen in einer Spalte unter Umständen als lineare Abbildungen verstanden werden, wobei auch andere Basis-Begriffe zugrunde liegen.

Einen speziellen Fall bilden Hilberträume. Seien also $U,V$ Hilberträume und $(u_{i})_{i\in I},(v_{i})_{i\in I}$ Orthonormalbasen von $U$ bzw. $V$. Dann erhält man eine Matrixdarstellung eines linearen Operators $f\colon U\to V$ (für lediglich dicht definierte Operatoren funktioniert es ebenso, falls der Definitionsbereich eine Orthonormalbasis besitzt, was im abzählbardimensionalen Fall stets zutrifft), indem man die Matrixelemente $f_{i,k}:=\langle u_{i},fu_{k}\rangle$ definiert; dabei ist $\langle u,v\rangle$ das Skalarprodukt im betrachteten Hilbertraum (im komplexen Fall semilinear im ersten Argument).

Dieses sogenannte Hilbert-Schmidt-Skalarprodukt lässt sich im unendlichdimensionalen Fall nur noch für eine bestimmte Teilklasse von linearen Operatoren, die sogenannten Hilbert-Schmidt-Operatoren, definieren, bei denen die Reihe, über die dieses Skalarprodukt definiert ist, stets konvergiert.

Literatur

• Maxime Bôcher: Einführung in die höhere Algebra. Teubner, Leipzig 1925 (XII, 348 S.). 

• Ewald Bodewig: Matrix calculus. 2nd, revised and enlanged edition Auflage. North-Holland Pub. Co., Amsterdam 1959, ISBN 978-1-4832-7498-0 (452 S.). 

• Richard Bellman: Introduction to matrix algebra. McGraw, New York 1960 (328 pages). 

• Rudolf Kochendörffer: Determinanten und Matrizen. 2. Auflage. B. G. Teubner, Leipzig 1961 (VI, 144 S.). 

• Richard S. Varga: Matrix Iterative Analysis. Prentice-Hall, Englewood Cliffs, NJ 1962, ISBN 0-13-565507-2 (XIII, 322 S.).  Matrix Iterative Analysis. 2. rev. and expanded ed., 1. softcover printing. Springer, Berlin, Heidelberg 2009, ISBN 978-3-642-05154-8 (X, 358 S., eingeschränkte Vorschau in der Google-Buchsuche). 

• Lothar Collatz: Eigenwertaufgaben mit technischen Anwendungen. 2., durchges. Auflage. Akad. Verl.-Ges. Geest & Portig, Leipzig 1963 (XIV, 500 S.). 

• Alston S. Householder: The Theory of Matrices in Numerical Analysis. Dover Publications Inc., New York NY 1964, ISBN 0-486-61781-5 (xi, 257 p.).  The theory of matrices in numerical analysis. Dover edition Auflage. Dover Publications, Mineola N.Y. 2006, ISBN 0-486-44972-6 (xi, 257 p., eingeschränkte Vorschau in der Google-Buchsuche).  Die Zahlen, aus denen sich die Matrix zusammensetzt, werden von Householder element/elements genannt, die Namen entry/entries verwendet er nicht.

• Rudolf Zurmühl: Matrizen und ihre technischen Anwendungen. 4., neubearbeite Auflage. Springer, Berlin, Göttingen, Heidelberg 1964 (XII, 452 S.). 

• Fritz Neiss: Determinanten und Matrizen. Siebente Auflage. Springer Berlin Heidelberg, Berlin, Heidelberg 1967, ISBN 978-3-662-00943-7 (VII, 111 S.). 

• Wolfgang Gröbner: Matrizenrechnung. Bibliogr.Inst, Mannheim 1977, ISBN 3-411-00103-8 (279 S.). 

• Dmitri K. Faddejew, Wera N. Faddejewa: Numerische Methoden der linearen Algebra. 5. Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1978 (782 S.). 

• Feliks R. Gantmacher: Matrizentheorie. VEB Deutscher Verlag der Wissenschaften, Berlin 1986, ISBN 3-326-00001-4 (654 S.). 

• Rudolf Zurmühl, Sigurd Falk: Matrizen und Ihre Anwendungen. 7., Softcover reprint of the original 7th ed. 1997. Springer, Berlin, Heidelberg, New York 2013, ISBN 978-3-642-63821-3 (XIV, 496 S.). 

• Gilbert Strang: Lineare Algebra. Springer-Verlag, Berlin 2003, ISBN 3-540-43949-8 (XII, 656 S., eingeschränkte Vorschau in der Google-Buchsuche).  Übersetzung der englischen Originalausgabe: Gilbert Strang: Introduction to linear algebra. 2. Auflage. Wellesley-Cambridge Press, Wellesley, Mass. 1998, ISBN 0-9614088-5-5 (VII, 503 p.). 

• Christian Voigt, Jürgen Adamy: Formelsammlung der Matrizenrechnung. Oldenbourg, München, Wien 2007, ISBN 978-3-486-58350-2 (XIV, 162 S., eingeschränkte Vorschau in der Google-Buchsuche). 

• Gene H. Golub, Charles F. van Loan: Matrix computations. Fourth edition Auflage. The Johns Hopkins University Press, Baltimore 2013, ISBN 978-1-4214-0794-4 (xxi, 756 pages, eingeschränkte Vorschau in der Google-Buchsuche). 

• Albrecht Beutelspacher: Lineare Algebra: Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 8., aktualisierte Auflage. Springer Spektrum, Wiesbaden 2014, ISBN 978-3-658-02412-3 (XIV, 368 S., eingeschränkte Vorschau in der Google-Buchsuche). 

• Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 18., aktualisierte Auflage. Springer Spektrum, Wiesbaden 2014, ISBN 978-3-658-03944-8 (XXI, 384 S., eingeschränkte Vorschau in der Google-Buchsuche). 

• Klaus Jänich: Lineare Algebra. 11. Auflage. Springer, Berlin u. a. 2008, ISBN 978-3-540-75501-2.

• Karsten Schmidt, Götz Trenkler: Einführung in die Moderne Matrix-Algebra – Mit Anwendungen in der Statistik. 3. Auflage. Springer, Berlin / Heidelberg 2015, ISBN 978-3-662-46772-5, doi:10.1007/978-3-662-46773-2. 

• Hermann Schichl, Roland Steinbauer: Einführung in das mathematische Arbeiten. 3., überarb. Auflage 2018. Springer Berlin Heidelberg, Berlin, Heidelberg 2018, ISBN 978-3-662-56806-4 (xvii, 531 S., eingeschränkte Vorschau in der Google-Buchsuche). 

• Günter M. Gramlich: Lineare Algebra: Eine Einführung. 5., überarbeitete Auflage. Carl Hanser Verlag, München 2021, ISBN 978-3-446-47188-7 (249 S., eingeschränkte Vorschau in der Google-Buchsuche). 

Weblinks

Wiktionary: Matrix – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Matrix – Sammlung von Bildern, Videos und Audiodateien

• Rechner für Matrizenmultiplikation, Determinantenberechnung, Eigenwerte und Eigenvektoren sowie Lineare Gleichungssysteme.
• The Matrix Cookbook – Eine englischsprachige, umfangreiche Matrix-Formelsammlung (PDF; 522 kB).