Regelungstechnik
Regelungstechnik ist eine Ingenieurwissenschaft, welche diejenigen Regelungsvorgänge behandelt, die in der Technik vorkommen.

Ein technischer Regelvorgang ist eine gezielte Beeinflussung von physikalischen, chemischen oder anderen Größen in technischen Systemen. Die sogenannten Regelgrößen sind dabei auch beim Einwirken von Störungen entweder möglichst konstant zu halten (Festwertregelung) oder so zu beeinflussen, dass sie einer vorgegebenen zeitlichen Änderung folgen (Folgeregelung).
Das Regelprinzip ist der Soll-Istwertvergleich der Führungsgröße mit der negativ zurückgeführten gemessenen Regelgröße. Der Regler bestimmt über die Regelabweichung (Regeldifferenz) und die vorgegebenen Regelparameter eine Stellgröße. Diese wirkt über die Regelstrecke so auf die Regelgröße ein, dass sie die Regelabweichung trotz vorhandener Störgrößen minimiert und die Regelgröße je nach gewählten Gütekriterien ein gewünschtes Zeitverhalten annimmt.
Bekannte Anwendungen im Haushalt sind die Konstant-Temperaturregelung für die Raumluft (Heizungsregelung), für die Luft im Kühlschrank oder für das Bügeleisen. Mit dem Tempomat wird die Fahrgeschwindigkeit im Kraftfahrzeug konstant gehalten. Eine Folgeregelung ist im Allgemeinen technisch anspruchsvoller, beispielsweise die Kursregelung mit einem Autopiloten in der Schifffahrt, Luftfahrt oder Raumfahrt, oder die Zielverfolgung eines beweglichen Objekts.
Die Regelungstechnik befasst sich auch mit der mathematischen Systemanalyse und Modelldefinition für Regelkreise und ihre Komponenten, um sie mit Differenzialgleichungen, Übertragungsfunktionen und Zustandsraumdarstellungen zu beschreiben. Damit lässt sich das jeweilige Systemverhalten berechnen und ein optimaler Regler entwerfen. Diese mathematische Systembeschreibung wird in der übergeordneten Systemtheorie (Ingenieurwissenschaften) behandelt und auch auf andere dynamische Systeme wie beispielsweise Wirtschaft oder Klima angewandt.
Dieser Hauptartikel Regelungstechnik stellt überschlägig das Spektrum der Regelungstechnik dar und bezieht sich dabei auf die Artikel Regelkreis, Regler, Regelstrecke und andere.
Geschichte der Regelungstechnik[Bearbeiten | Quelltext bearbeiten]
Die Beschäftigung des Menschen mit der Regelungstechnik begann zwischen dem 3. Jahrhundert v. Chr. und dem 1. Jahrhundert n. Chr. im antiken Griechenland. Das einer Regelung zugrunde liegende Rückkopplungsprinzip ist keine Erfindung des Menschen, sondern ein seit je stattfindendes Naturphänomen. Die moderne Regelungstechnik begann zur Zeit der industriellen Revolution unter Verwendung mechanischer Bauteile. Ihr größter Fortschritt wurde durch die Entwicklung der Elektronik und schließlich durch die elektronische Rechentechnik ermöglicht.
Erklärung und Definition von Regelung und Steuerung[Bearbeiten | Quelltext bearbeiten]
Einschlägige Normen[Bearbeiten | Quelltext bearbeiten]
In der Automatisierungstechnik spielen neben Regelungen auch Steuerungen eine sehr wichtige Rolle. Zur Geschichte der Normung von Regelung und Steuerung sind im Artikel Steuerungstechnik nähere Ausführungen zu finden.
Die Norm „IEC 60050-351 Internationales Elektrotechnisches Wörterbuch – Teil 351: Leittechnik“ legt Grundbegriffe der Leittechnik fest, unter anderen auch Prozess und Leiten, und schließt dabei die Regelung und die Steuerung mit ein. Sie ersetzt in Deutschland die DIN-Norm DIN V 19222:2001-09. Die früher gültige Norm DIN 19226 für die Definition regelungstechnischer und steuerungstechnischer Begriffe ist seit dem Jahre 2002 nicht mehr gültig.
In der englischsprachigen Fachliteratur wird undifferenziert sowohl für Regelung als auch für Steuerung das englische Wort control (für den Prozess) bzw. controller (für die hardwaremäßige Implementierung) verwendet. Dieser Begriff wird meistens mit Steuerung übersetzt. Um richtig übersetzen zu können, ist daher die Kenntnis des Kontextes erforderlich. Wenn control engineering verwendet wird, ist eindeutig Regelungstechnik gemeint.
Definition des Begriffs Regelung[Bearbeiten | Quelltext bearbeiten]
Die Norm DIN IEC 60050-351 enthält folgende Definition des Begriffs Regelung:
- Die Regelung bzw. das Regeln ist ein Vorgang, bei dem fortlaufend eine Größe, die Regelgröße, erfasst, mit einer anderen Größe, der Führungsgröße, verglichen und im Sinne einer Angleichung an die Führungsgröße beeinflusst wird.
- Kennzeichen für das Regeln ist der geschlossene Wirkungsablauf, bei dem die Regelgröße im Wirkungsweg des Regelkreises fortlaufend sich selbst beeinflusst.
Erweiterte Erklärung des Begriffs Regelung[Bearbeiten | Quelltext bearbeiten]
Oben genannter Definition liegt der Wirkungsplan für eine einschleifige Eingrößen-Regelung zugrunde, wie diese in der Praxis am häufigsten auftritt. Darin sind die einzelnen Größen wie die Regelgröße, die Führungsgröße sowie die nicht genannte, zur Führungsgröße rückgeführte Messgröße, die Stellgröße und die Störgröße als zeitlich veränderliche Größen zu betrachten.

Die Regelgröße wird durch ein Messglied als Istwert gemessen und dieser mit der Führungsgröße (Sollwert) verglichen. Die Regelabweichung als Differenz zwischen dem Sollwert und dem Istwert wird dem Regler zugeführt, der daraus entsprechend dem gewünschten Zeitverhalten (Dynamik) des Regelkreises eine Stellgröße bildet. Das Stellglied kann Bestandteil des Reglers sein, in den meisten Fällen stellt es jedoch ein separates Gerät dar. Die Störgröße wirkt auf die Regelgröße in der Regelstrecke oder Teilen von ihr.
Für die gewollte Minimierung der Regelabweichung (bzw. Regeldifferenz) hängt die Polarität der Regelabweichung nicht nur von der Führungsgröße ab, sondern auch vom Wirkungssinn der Regelstrecke (direkt oder invertierend).
Eine positive Regelabweichung führt über die Verstärkung des Reglers nur dann zu einer positiven Zunahme der Regelgröße, wenn die Regelstrecke zur Reduzierung der Regelabweichung einen positiven Stellwert benötigt. Handelt es sich bei einer Regelstrecke z. B. um eine Heizung, so führt ein positiver Stellwert zu einer steigenden Temperatur. Das Öffnen eines Fensters, Sonneneinstrahlung oder Kühleffekte durch Windgeschwindigkeit sind von außen wirkende Störgrößen. Handelt es sich bei der Regelstrecke z. B. um ein Kühlaggregat, so führt ein positiver Stellwert (also das Einschalten der Kompressionskältemaschine) zu einer sinkenden Temperatur. Ein solcher Fall ist im Blockschaltbild des Regelkreises durch eine Vorzeichenumkehr der Stellgröße gekennzeichnet.
Prinzipien der Steuerung[Bearbeiten | Quelltext bearbeiten]
Die Norm DIN IEC 60050-351 enthält folgende Definition des Begriffs Steuerung:
- Das Steuern, die Steuerung, ist ein Vorgang in einem System, bei dem eine oder mehrere Größen als Eingangsgrößen, andere Größen als Ausgangs- bzw. Steuergrößen aufgrund der dem System eigentümlichen Gesetzmäßigkeiten beeinflussen.
- Kennzeichen für das Steuern ist entweder der offene Wirkungsweg oder ein zeitweise geschlossener Wirkungsweg, bei dem die durch die Eingangsgrößen beeinflussten Ausgangsgrößen nicht fortlaufend und nicht wieder über dieselben Eingangsgrößen auf sich selbst wirken.
Beim Wirkungsplan von Steuerungen entfällt gegenüber dem Wirkungsplan der Regelung die über das Messglied der Regelgröße vollzogene Rückführung (Rückkopplung). Die Führungsgröße bildet über die Steuereinrichtung eine Stellgröße, die über die Steuerstrecke direkt die Ausgangsgröße bestimmt.

Bleibt die zu steuernde Größe von außen ungestört, arbeitet eine reine Steuerung bei gut bekannter Steuerstrecke fehlerfrei. Sind die Störungen messbar, können sie durch geeignete Maßnahmen kompensiert werden. Beispielsweise ist die Energiezufuhr für eine Heizungseinrichtung, bei der nur die Vorlauftemperatur des Heizmediums gegen schwankende Außentemperatur geregelt wird, eine offene Steuerung. Wird ein Fenster des Raumes zur kalten äußeren Umgebung geöffnet, wirkt eine Störgröße auf die Raumtemperatur , und diese sinkt. Für ihre Regelung müsste sie gemessen und auf eine Regeleinrichtung gegengekoppelt werden.
Der Wirkungsplan in der Abbildung zeigt eine Steuerung, die als offene Kette aus Steuereinrichtung und Steuerstrecke dargestellt ist. Wenn eine Störgröße dominant und bekannt und messbar ist, kann zusätzlich eine Störgrößenaufschaltung, die einen zweiten Zweig der Steuerung darstellt, angewendet werden (oberer Block in der Abbildung).
Vor- und Nachteile von Regelungen gegenüber Steuerungen[Bearbeiten | Quelltext bearbeiten]
Vorteile von Regelungen:
- Störungen einer Größe in einem Prozess sind oft in Größe und zeitlichem Auftreten nicht bekannt und deshalb nicht erfassbar. Das ist im Vergleich mit einer Steuerung der grundsätzliche Vorteil einer Regelung, mit der eine Größe gegen den Einfluss beliebiger Störungen annähernd auf einen gewünschten Wert gehalten wird, ohne dass die Störungen bekannt sein müssen.
Nachteile von Regelungen:
- Eine Regelung ist technisch aufwändiger und teurer als eine Steuerung, weil sie die Steuergröße als Regelgröße messen und die Stellgröße mit einem geeigneten Regler ermitteln muss. Eine Steuerung ist nur dann vorteilhaft, wenn die Auswirkung von Störgrößen toleriert werden kann und an Genauigkeit und Konstanz der Steuergröße keine hohen Anforderungen bestehen.
- Der Regelkreis kann durch ungewollte, z. B. durch Alterung und Verschleiß bedingte Parameteränderungen instabil werden.
- Heuristische Optimierungsverfahren und Reparaturen nach dem Prinzip „Versuch und Irrtum“ reichen oft nicht aus. Qualifizierte Fachleute sind erforderlich.
Die Vor- und Nachteile von Steuerungen sind im Artikel Steuerungstechnik beschrieben.
Technische Realisierung der Regelung und Steuerung[Bearbeiten | Quelltext bearbeiten]

Die Eingangs- und Ausgangsgrößen sowie deren Verarbeitung in einem Steuerungs- oder Regelungssystems können durch Analogtechnik oder Digitaltechnik realisiert werden.[1][2][3] Analoge Systeme werden heute weitgehend ersetzt durch digitale Systeme, die die Automatisierung durch Fernsteuerung, Fernwartung und Vernetzung im Sinne von Industrie 4.0 unterstützen und zudem meist kostengünstiger herzustellen sind. In Sonderfällen werden pneumatische oder einfache mechanische Regler eingesetzt.
Je nach Aufbau und Einsatzzweck lassen sich unterscheiden:
- Industrieregler: Maschinennahe Einzelregler für Kleinanlagen mit eigenem Mikroprozessor
- Prozessregelgeräte: Erweiterbare Industrieregler mit Schnittstelle zu übergelagertem (Leit-)System
- Universalregler: Prozessregler in Form von Erweiterungskarten oder Software-Regelbausteinen für programmierbare Steuerungen
- Branchenregler: Spezielle Prozessregler, die für bestimmte Anwendungsgebiete optimiert sind
Analogtechnik[Bearbeiten | Quelltext bearbeiten]
Analogsignale sind wert- und zeitkontinuierlich und weisen daher einen stufenlosen und beliebig feinen Verlauf auf. Die Grenzen der Signalauflösung sind durch parasitäre Signalrauschanteile gegeben. Bei Anwendung von Abschirmmaßnahmen und Signalfiltern lässt sich die Signalauflösung verbessern. Der Steuer- bzw. Regeleingriff erfolgt stetig ohne Verzögerung und ist damit auch für hoch-dynamische Regelkreise geeignet.
Analoge Regelungssysteme basieren meist auf Analogelektronik mit Operationsverstärkern und Analogmultiplizierern für die Grundrechenarten. Die Vorgabe der Führungsgröße und die Einstellwerte für den Regler wird meist durch Potentiometer realisiert. In seltenen Fällen werden auch pneumatische Regler verwendet.
Digitaltechnik[Bearbeiten | Quelltext bearbeiten]
Digitale Systeme weisen einen nichtstetigen Verlauf mit diskreten Werten für Messwerte und Stellgrößen, die mit einer vorgegebenen Abtastrate aktualisiert werden. Mit heute verfügbaren Technologien ist sowohl die Auflösung der Systemgrößen als auch die verfügbare Rechenleistung so hoch, dass die Leistung von analogen Systemen in fast allen Anwendungsfällen übertroffen wird und bei komplexeren System sogar kostengünstiger umgesetzt werden kann. Es bleibt jedoch das systemische Risiko von unentdeckten Softwarefehlern, die unzulässige oder katastrophale Auswirkungen haben können.
Speicherprogrammierbare Steuerungen (SPS) verarbeiten die binären Eingangssignale über das digitale Rechenwerk zu binären Ausgangssignalen. Das Rechenwerk wird über ein Programm gesteuert, das in Speichern abgelegt ist.
Speicherprogrammierbare Steuerungen sind modular aufgebaut und werden von vielen Herstellern angeboten. Sie können damit einfache Schaltwerke für kombinatorisches und sequenzielles Verhalten für aufeinander folgende Funktionsabläufe (Ablaufsteuerungen) realisieren. Der sequentielle Ablauf kann mit einer Rückmeldung als vollzogene Bestätigung eines Steuervorgangs verbunden sein und entspricht damit einer zeitweise geschlossenen Steuerung.[4]:41–43 Es können auch digitale oder analoge Teilsysteme eingebunden sein. Analoge Messwerte werden dabei zeitdiskret abgetastet und mit Analog-Digital-Umsetzern in diskrete Digitalwerte umgesetzt. Digitale Ausgangssignale können mit Digital-Analog-Umsetzern oder Pulsweitenmodulation für analog arbeitende Stellglieder aufbereitet werden. Schrittmotoren werden direkt angesteuert.
Die Steuereinrichtungen beeinflussen die Regelstrecke oder einen technischen Prozess über Bedienelemente wie Signalgeber (Schalter, Taster, Tastaturfeld) mit Steuerfunktionen wie Schalt-, Zähl-, Zeit-Vergleicher und Speichervorgängen sowie zeitliche Ablauffunktionen. Soweit physikalische analoge Größen überwacht oder geregelt werden, sind die entsprechenden Sensoren erforderlich. Auch Noteingriffe für die automatische Abschaltung des Prozesse, teilweise mit geordnetem Herunterfahren, können erforderlich werden.
Innerhalb der Steuerstrecke oder deren Ausgängen findet der Prozessablauf statt. Stellglieder und Aktoren jeglicher Art (Motoren, Ventile, Pumpen, Förderbänder, Schaltschütze), Hydraulik- und Pneumatikelemente, Stromversorgung, Regler wirken auf den Prozess. Ausgangssignale beziehen sich auf die Überwachung des Prozesses und sind durch Signallampen, alphanumerische Anzeigen, Fehlermeldungstableaus, akustische Signalgeber, Protokollschreiber usw. realisiert.[4]:35–50
Anwendungen digitaler Steuerungs- und Regelungstechnik sind beispielsweise Offset-Rotationsmaschinen für Druckerzeugnisse, die Automatisierung chemischer Produktionsanlagen und Kernkraftwerke.
Digitaltechnik und Vernetzung erhöhen die Risiken von katastrophalen Programmfehlern[5] sowie unbeherrschbaren Situationen, wie z. B. im Fall der beiden Abstürze der Boeing 737 Max aufgrund der Schwächen des Maneuvering Characteristics Augmentation System (MCAS).[6] Technische Prozesse können durch Cyberattacken angegriffen werden, wie mit dem Stuxnet-Computerwurm auf iranische Zentrifugen zur Urananreicherung.
Sonstige Realisierungen[Bearbeiten | Quelltext bearbeiten]
Sehr einfache mechanische Regler benötigen keine Hilfsenergie. Der Bimetallthermostat eines Bügeleisens schließt den elektrischen Kontakt der Heizung, solange die Solltemperatur nicht erreicht ist. Danach ergibt sich aufgrund der Verzögerung der Messung und der Schalthysterese des Kontakts ein quasi-periodisches Ein- und Ausschalten, bei dem die Temperatur der Bügelfläche mit wenigen Kelvin Abweichung um den Sollwert pendelt.
Pneumatische Regler benötigen Druckluft als Hilfsenergie. Sie werden vor allem in Anwendungen eingesetzt, die Explosionsschutz erfordern und die Gefahr von Funkenbildung unbedingt vermieden werden muss.[7]
- Beispiele von Steuer- und Regelgeräten (Zeitraum 1788–2016)
-
Fliehkraftregler einer Boulton & Watt Dampfmaschine (1788)
-
Pneumatischer PID-Regler Telepneu von Siemens & Halske (ca. 1960)
-
Zeitgesteuerter Raumtemperaturregler flexostat von Sauter (1967)
-
Hybrid aufgebautes Antiblockiersystem von Bosch (1978)
-
Kompaktregler RU 5X für Heizungsanlagen von R+S Regler (ca. 2005)
-
Modulare SPS ControlLogix von Allen-Bradley (2013)
-
Kompakt-SPS für Kleinsteuerungen Logo! von Siemens (2016)
Werkzeuge für Rapid Prototyping in Forschung und Entwicklung[Bearbeiten | Quelltext bearbeiten]
In der Forschung und Entwicklung entsteht regelmäßig das Problem, neue Regelungskonzepte zu testen. Die wichtigsten Software-Werkzeuge für rechnergestützte Analyse, Entwurf und Rapid Control Prototyping sowie Simulation von Regelungen sind nachfolgend aufgeführt.
- GNU Octave, Free Software Foundation
- Eine freie Software zur numerischen Lösung mathematischer Probleme, wie zum Beispiel Matrizenrechnung, Lösen von (Differential-)Gleichungssystemen, Integration. Berechnungen können in Octave mit einer Skriptsprache durchgeführt werden, die weitgehend zu dem proprietären Matlab (aber nicht Simulink) kompatibel ist.
- MATLAB und Simulink, The MathWorks
- Durch zahlreiche Toolboxes ein sehr umfangreiches Softwarepaket für numerische Mathematik, für Simulation, Systemidentifikation, Reglerentwurf und Rapid Control Prototyping geeignet (kommerziell)
- Scilab, Institut National de Recherche en Informatique et en Automatique (INRIA)
- Ebenfalls sehr umfangreiches Softwarepaket für numerische Mathematik mit ähnlichem Konzept und ähnlicher Syntax wie MATLAB, für Simulation, Systemidentifikation und Rapid Control Prototyping geeignet (frei)
- CAMeL-View TestRig
- Entwicklungsumgebung zur Modellbildung von physikalischen Systemen mit dem Schwerpunkt Reglerentwurf und Rapid Control Prototyping sowie zur Anbindung an Versuchsstände (kommerziell)
- Maple
- Computeralgebrasystem (CAS), beherrscht numerische und symbolische Mathematik, besonders für manche Entwurfsverfahren der nichtlinearen Regelung geeignet (kommerziell)
- Mathematica, Wolfram Research, Inc.
- Umfangreiches Softwarepaket für numerische und symbolische Mathematik (kommerziell)
- dSPACE
- Integrierte Hard- und Software-Lösungen für die Anbindung von MATLAB an Versuchsstände (kommerziell)
- LabVIEW, National Instruments (NI)
- Integrierte Hard- und Software-Lösungen für die Rechnersteuerung von Versuchsständen (kommerziell)
- ExpertControl
- Software-Lösungen für vollautomatische Systemidentifikation und vollautomatische, modellbasierte Reglerauslegung für klassische Reglerstrukturen (PID-Regler) sowie Reglerstrukturen für Systeme höherer Ordnung (kommerziell)
- TPT
- Systematisches Testwerkzeug für Regelungssysteme, das neben der Simulation auch eine Ergebnisauswertung und Analysemöglichkeit bietet.
Alle aufgeführten Werkzeuge zeigen ein hohes Maß an Flexibilität bezüglich der Anwendung und der verwendbaren Reglerstrukturen.
Technische Anwendungen[Bearbeiten | Quelltext bearbeiten]



- Bahntechnik
- In der Antriebsregelung treten vielfältige Regelungsprobleme auf, es sind beispielsweise Drehmoment und Geschwindigkeit zu regeln. An der U-Bahn Sendai wurde die Fuzzy-Regelung erfolgreich eingesetzt.
- Luftfahrt
- Regelungsprobleme treten in zahlreichen Komponenten von Flugzeugen auf, etwa in den Turbinen, aber auch bezogen auf die Flugdynamik. Beispiele für flugdynamische Regelungsprobleme sind die Kontrolle der Roll-, Gier- und Nickwinkel, sowie der Autopilot. Siehe auch Flugsteuerung.
- Energietechnik
- Stellungsregelung eines Stellventils mit Stellantrieb innerhalb einer Reglerkaskade. Im Verbundnetz der Stromversorgung sind Spannung und Frequenz netzweit zu halten. In jedem Kraftwerk werden Spannung und Frequenz lokal geregelt, so dass die Aufgabe mit dezentralen Reglern durch Variation der Regelleistung gelöst wird (siehe auch Kraftwerk). Global werden lediglich die Leistungssollwerte der einzelnen Kraftwerke vorgegeben.
- Kraftfahrzeugtechnik
- Tempomat und Antiblockiersystem (ABS), aber auch elektronisches Stabilitätsprogramm (ESP) sind bekannte Regelungen im Fahrzeugbereich, die auch als Fahrerassistenzsysteme bezeichnet werden. Auch Verbrennungsmotoren beinhalten vielfältige Regelkreise, beispielsweise für die Leerlaufdrehzahl, das Luftverhältnis (siehe auch Lambdasonde), die Klopfregelung (siehe auch Klopfen (Verbrennungsmotor)). Moderne automatische Schaltgetriebe benötigen Regelkreise für die Synchronisation beim Schalten.
- Elektroantrieb
- Bei Fahrzeugen mit elektrischem Antrieb werden Elektromotoren mit größeren Leistungen eingesetzt. Diese werden über eine Drehzahl- und Drehmomentregelung angesteuert, bei Hybridfahrzeugen auch in Verbindung mit dem Verbrennungsmotor.
- Pipeline
- In Pipelines kommen vor allem vermaschte Regelungen vor, für Durchfluss, Druckregelung (Vordruck, Nachdruck) und Stellungsregelung einschließlich Grenzwertregelung.
- Robotik
- In der Fertigungsautomatisierung sind die Achsen der Fertigungsroboter zu positionieren. Hier spielen eine schnelle Beruhigungszeit und geringstes Überschwingen eine besonders große Rolle.
- Verfahrenstechnik
- In verfahrenstechnischen Prozessen werden chemische und physikalische Größen geregelt, die im betrachteten Prozess eine Rolle spielen. Beispiele sind die Regelung von Füllstand, Temperatur, pH-Wert und Sauerstoffgehalt eines Rührkessel-Reaktors oder das Konstanthalten von Stoff- bzw. Ionenkonzentrationen mit einem Chemostat.
- Wasserwirtschaft
- Zur Vermeidung von Überschwemmungen und Sicherung der Wasserversorgung sind unterlagerte Regelungen von Ketten von Talsperren bedeutsam. Der Füllstand eines einzelnen Stausees wird von einem übergeordneten Management vorgegeben und lokal geregelt.
Regelkreis-Entwurfsstrategien[Bearbeiten | Quelltext bearbeiten]
Die Aufgabe des Reglers besteht darin, die Regelgröße der Führungsgröße möglichst gut anzunähern und den Einfluss von Störgrößen zu minimieren. Die Führungsgröße kann als fester Sollwert, als programmgesteuerte Sollwertvorgabe oder als kontinuierliches, zeitabhängiges Eingangssignal mit besonderen Folgeeigenschaften für die Regelgröße ausgelegt sein.
Eine der Regelstrecke nicht angepasste zu hohe Kreisverstärkung kann bei Regelstrecken mit mehreren Verzögerungsgliedern oder gar mit Totzeitverhalten zur oszillatorischen Instabilität führen. Bedingt durch die Zeitverzögerung in der Regelstrecke wird über den Soll-Istwert-Vergleich dem Regler die Regeldifferenz verspätet zugeführt. Diese nacheilende Verschiebung der Regelgröße kann am Soll-Istwert-Vergleich anstelle einer Gegenkopplung eine Mitkopplung bewirken, und der geschlossene Regelkreis wird hierdurch instabil und baut Dauerschwingungen auf.
Regelkreis-Entwurfsstrategien für lineare Systeme[Bearbeiten | Quelltext bearbeiten]
Die Entwurfsstrategien für Regelkreise beziehen sich bei linearen Systemen auf die Optimierung des statischen Verhaltens und des Zeitverhaltens des jeweiligen geschlossenen Regelkreises. Je geringer beispielsweise die Zeitverzögerungen der Regelstrecke sind, umso höher kann die sog. Kreisverstärkung und damit die Verstärkung des Reglers gewählt werden, was die statische Genauigkeit der Regelung verbessert.
Eine hohe Kreisverstärkung macht den Regelkreis auch dynamisch schnell, sie kann aber praktisch nur begrenzt realisiert werden, weil die Stellgröße wegen technischer Anschläge oder aus Energiemangel nicht unbegrenzt wachsen kann. Eine geringere Regler-Verstärkung in Verbindung mit einer zeitlich integral wirkenden Komponente des Reglers macht den Regelkreis für alle statischen Einflüsse zwar genauer und stabiler, aber eben auch langsamer. Hierzu muss mittels einer geeigneten Entwurfsstrategie eine optimierte Kompromisslösung gefunden werden. Zur Beurteilung wurde dazu der Begriff Regelgüte definiert, der es erlaubt, das unvermeidliche periodisch gedämpfte Einschwingverhalten der Regelgröße in Regelkreisen mit Regelstrecken höherer Ordnung abzuschätzen.
Regelkreis-Entwurfsstrategie bei gemischten linearen und nichtlinearen Systemen[Bearbeiten | Quelltext bearbeiten]
Die Entwurfsstrategie bei gemischten linearen und nichtlinearen Systemen ist komplizierter und bezieht sich auf Modelle wie z. B. das Hammerstein-Modell, bei dem eine statische Nichtlinearität in Verbindung mit einem dynamischen linearen System zusammenwirkt. Das Verhalten unstetiger nichtlinearer statischer Regler in Verbindung mit linearen Regelstrecken kann mit dem Verfahren der harmonischen Balance behandelt werden.
Regler in Regelkreisen mit nichtlinearen und linearen Komponenten lassen sich sinnvoll mit der numerischen Mathematik behandeln, insbesondere mit modernen Simulationswerkzeugen, wie diese auch für Personal Computer (PC) zur Verfügung stehen.
Zur Bestimmung des Systemverhaltens der Regelstrecke und des Reglers sind verschiedene theoretische und experimentelle Analysemethoden und mathematische Entwurfsverfahren üblich. Die Grundlagen zur mathematischen Behandlung und die speziellen Verfahren für die Regelungstechnik folgen in den nachstehenden Kapiteln.
Zweigrößenregelung als Beispiel für Mehrgrößensysteme[Bearbeiten | Quelltext bearbeiten]
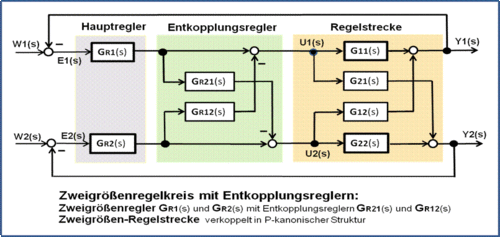
Prinzipiell ist die Regelung einer Regelstrecke als Mehrgrößensystem ähnlich dem Eingrößensystem. Sie erfordert die Analyse der Kopplungselemente und damit einen höheren mathematischen Aufwand für die Regelkreisauslegung.[9] Für eine Mehrgrößen-Regelung ist kennzeichnend, dass eine einzige Stellgröße als Eingangsgröße der Regelstrecke stets mehrere Ausgangsgrößen (Regelgrößen) beeinflusst (hier über die Faktoren G21 und G12). Wenn eine Klimaanlage sowohl die Temperatur als auch die relative Feuchte auf Sollwerte regeln soll, dann führt ein Stelleingriff in die Heizung zur Temperaturerhöhung und – physikalisch bedingt – gleichzeitig zum Absinken der relativen Feuchte . Ein Stelleingriff in die Befeuchtungseinrichtung zur Feuchteerhöhung senkt zugleich die Temperatur im klimatisierten Raum. Über den Entkopplungsregler wird der Regeleingriff so optimiert, dass bei einer Temperaturerhöhung gleichzeitig mehr Feuchte zugeführt wird (Faktor GR21).
Beispiel der Heizungsregelung eines Gebäudes[Bearbeiten | Quelltext bearbeiten]
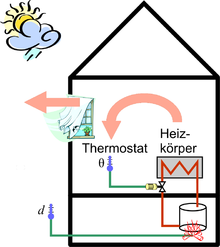
Als einfaches, anschauliches Beispiel für einen Standard-Regelkreis soll hier die Regelung der Raumtemperatur auf Grundlage einer Warmwasser-Zentralheizung und deren Gerätekomponenten dienen.
Gasheizkessel, Ölheizkessel und Feststoffheizkessel gewinnen die Wärmeenergie aus der Verbrennung meist fossiler Brennstoffe und transportieren die Wärmeenergie über den Wärmeträger Wasser. Ein über eine Brennkammer erhitzter Heizkessel ist mit Hilfe einer Heizungspumpe an einen Warmwasserkreislauf mit Heizkörpern und/oder Fußbodenheizung angeschlossen.
Die Wärmezufuhr des Heizkörpers erwärmt die umgebende Raumluft durch Konvektion und Strahlung. Die Wärmeenergie mit dem Temperaturgefälle zwischen Heizkörper und Raumtemperatur fließt je nach Größe der Außentemperatur über die Fenster, Türen, Raumwände und Außendämmung an die Außenwitterung ab.
Dezentrale Raumtemperaturregelung[Bearbeiten | Quelltext bearbeiten]
Die an das Gebäude abgegebene Wärmemenge ist durch die Differenz der Vorlauf- und Rücklauftemperatur am Heizkessel und durch die Durchflussmenge des Wassers gegeben. Alle Heizkörper der Räume eines Gebäudes erhalten die gleiche meist nach der Außentemperatur gesteuerte Vorlauftemperatur. Die Heizkörper sämtlicher Räume sind mit Thermostatventilen ausgestattet.
Die Größe der Heizkörper ist an die jeweilige Raumgröße angepasst. Die für eine bestehende Außentemperatur erforderliche Vorlauftemperatur wird über einen Außentemperatur-Fühler erfasst und gesteuert. Wählbare Heizungskennlinien aus einem Kennlinienfeld berücksichtigen die unterschiedlichen Wärmeanforderungen von Gebäuden und damit die Beziehung Außentemperatur zur Vorlauftemperatur. Ziel ist das selbsttätige Halten der Raumtemperatur als Regelgröße auf einem gewünschten Sollwert mit Hilfe eines Thermostatventils.
Bei dem am Heizkörper befindliches Thermostatventil wird die gewünschte Solltemperatur des Raumes durch Drehen der Thermostat-Kappe innerhalb des Bereiches einer Skala eingestellt. Der Sensor des Thermostatventils misst die aktuelle Zimmertemperatur (Theta) und verändert über die Ventilstellung (Aktor) die Durchflussmenge des Warmwassers durch den Heizkörper und damit die in den Raum zugeführte Wärmemenge. Das Thermostatventil hat ein proportionales Regelverhalten (P-Regler), das auf Störgrößen etwas träge reagiert bei zunehmender Abweichung zwischen Soll- und Istwert bei niedrigen Außentemperaturen.
Gleichermaßen für die dezentrale Raumtemperaturregelung wie auch die zentrale Gebäudetemperaturregelung mit einem Referenzwohnraum gilt für moderne Heizungsanlagen die Verwendung eines modulierbaren Brenners mit stetigem Verhalten der Wärmeenergie-Erzeugung. Dieser Brenner kann beispielsweise im Bereich von ca. 10 bis 100 % je nach Anforderung seine Wärmeenergie stetig verändern. Den Bereich des stetigen Verhaltens des Brenners bezeichnet man heizungstechnisch als Modulationsgrad.
Brennwertkessel mit Gas sind in der Lage, die in den Abgasen enthaltene Wärme fast vollständig zu entziehen und zu nutzen.
Gegenüber einer Heizungsanlage mit intermittierendem Ein/Aus-Betrieb sind folgende Vorteile bei einem modulierbaren Brenner verbunden:
- Geringe thermodynamische Materialbeanspruchung im Brennerraum,
- Reduzierung der Brennergeräusche und Vermeidung von Ausdehnungs-Knackgeräuschen in den Rohrleitungen und
- Einsparung von Brennmaterial.
Unterhalb des nicht stetigen Bereiches des Brenners arbeitet dieser intermittierend mit erheblich reduzierter Wärmeanforderung.
Hauptregler für den Referenzwohnraum[Bearbeiten | Quelltext bearbeiten]
Neben der dezentralen Temperatur-Regelung der Wohnräume mit Thermostatventilen ist bei modernen Heizungsanlagen ein Referenzwohnraum (auch Pilotraum, Führungsraum, größter Wohnraum) eingerichtet, bei dem ein zentraler hochwertiger Hauptregler über einen Raumtemperatur-Sollwertgeber und einen Referenzraum-Temperaturfühler die Vorlauftemperatur für den gesamten Warmwasserkreislauf des Gebäudes zentral vorgibt und die Referenzraum-Temperatur regelt.
Die Temperaturunterschiede zwischen den Heizkörpern und der kühleren Raumluft erzeugen Luftbewegungen (Konvektion) und zum geringeren Anteil Strahlungsenergie, die auf den Messfühler einwirken. Der Regler erhöht je nach Bedarf durch Einschalten des Brenners die Vorlauftemperatur oder senkt sie gegebenenfalls durch Ausschalten des Brenners.
Für die Güte einer Regelung der Raumtemperatur sind auch die konstruktiven Raumbedingungen und Geräteanordnungen wie Heizkörper und Abstand des Messortes der Raumtemperatur maßgebend. Man kann nicht in einem langgestreckten Raum erwarten, dass durch einen Heizkörper mit dem im Abstand von 10 cm befindlichen Thermostat sich eine gleichmäßige Raumtemperatur über den ganzen Raum einstellt. Andererseits bedeutet ein großer Abstand zwischen Heizkörper und Messort der Raumtemperatur, dass sich eine größere Signallaufzeit (Totzeitverhalten) bildet.
Üblich ist die Montage des Messfühlers im Referenzwohnraum an der gegenüberliegenden Wand der Heizkörperebene. Der Messfühler misst die Lufttemperatur, nicht die Innenwand-Temperatur. Die Heizkörper des Referenzwohnraumes erhalten keine Thermostatventile.
Bezeichnungen für Komponenten und Signale des Regelkreises[Bearbeiten | Quelltext bearbeiten]
Anmerkung:
- In der deutschen Fachliteratur sind die regelungstechnischen Signalbezeichnungen nicht immer den gültigen DIN-Normen entnommen, sondern stammen teilweise vermutlich aus den Darstellungen von Signalflussplänen dynamischer Systeme des Zustandsraumes. Diese aus den USA von dem Mathematiker und Stanford-Universitätslehrer Rudolf Kálmán stammende Theorie und die damit verbundenen Signalbezeichnungen sind seit den 1960er Jahren unverändert.
- Einige Fachbücher der Regelungstechnik zeigen für die Darstellung von Signaleingängen und Signalausgängen von Übertragungssystemen auch die Bezeichnungen XA (Ausgangsgröße) und XE (Eingangsgröße).
| Bezeichnung | Zeichen wie bei Zustandsraum-Systemen | Zeichen nach DIN IEC 60050-351 |
Bedeutung allgemein und im Beispiel (Raumtemperatur-Regelung mit Thermostatventil) |
|---|---|---|---|
| Regelstrecke | GS(s) |
| |
| Störgröße | d | z |
|
| Regelgröße | y | x |
|
| Istwert |
| ||
| Messglied |
| ||
| Messgröße | yM | yM |
|
| Führungsgröße | w | w |
|
| Sollwert |
| ||
| Regelabweichung | e = w − y |
e = w − x |
|
| Regler | GR(s) |
| |
| Stellglied |
| ||
| Reglerstellgröße | uR | yR |
|
| Stellgröße | u | y |
|
Definition Wärmeenergie[Bearbeiten | Quelltext bearbeiten]
Umgangssprachlich wird die thermische Energie etwas ungenau als „Wärme“ oder „Wärmeenergie“ bezeichnet. Die thermische Energie eines Stoffes ist definiert als
wobei die spezifische Wärmekapazität, die Masse und die absolute Temperatur ist. Diese Definition setzt voraus, dass der Stoff sich innerhalb seines Aggregatzustandes befindet. Für Wasser gilt der flüssige Zustand im Temperaturbereich von 0(+) °C bis 100(-) °C bei Normaldruck in Meereshöhe.
Eine Wärmezufuhr steigert die mittlere kinetische Energie der Moleküle und damit die thermische Energie eines Stoffes, eine Wärmeabfuhr verringert sie.
Kommen zwei thermische Energie-Systeme mit unterschiedlichen Temperaturen zusammen, so gleichen sich ihre Temperaturen durch Wärmeaustausch an. Diese Angleichung erfolgt so lange, bis keine Temperaturdifferenz zwischen den Systemen mehr auftritt. Diesen Vorgang bezeichnet man als Wärmeübertragung.
Ohne zusätzliche Hilfe (Energie) kann niemals thermische Energie vom System niedrigerer Temperatur in das System höherer Temperatur überführt werden.
Der Wärmefluss oder Wärmestrom ist eine physikalische Größe zur quantitativen Beschreibung von Wärmeübertragungsvorgängen.
Als Grenzfläche oder Phasengrenze wird in der Physik und Materialwissenschaft die Fläche zwischen zwei Phasen (hier Phase = räumlicher Bereich der Materie Zusammensetzung wie Dichte der homogenen Materie) bezeichnet. Als Grenzflächen werden die Flächen zwischen flüssigen und festen, flüssigen und flüssigen, festen und festen und festen zu gasförmigen Phasen bezeichnet.
Alternative stetige und unstetige Regelung[Bearbeiten | Quelltext bearbeiten]
Zur Regelung der Referenzraumtemperatur bieten sich zwei Wege als stetige oder nichtstetige Regelung an:
Die Änderung der Außentemperatur ist in der Regel als statische Störgröße zu betrachten, weil das Zeitverhalten sehr langsam im Verhältnis zur Änderung der Vorlauftemperatur ist. Erst wenn die Änderung der Außentemperatur sich über die Außendämmung und über die Masse der Gebäudewände am Messfühler des Referenzraumes bemerkbar macht, kann der Heizungsregler reagieren.
Die Regelung der Raumtemperatur des Referenzraumes kann konventionell meist über digitale Regler erfolgen, die an die Regelstrecke des Warmwasserkreislaufes angepasst werden müssen.
Häufig werden industriell gefertigte Heizungskessel mit digitalen Reglern mit Anwendung der Fuzzy-Logik ausgeführt. Die Grundidee der Fuzzy-Controllers bezieht sich auf die Einbindung des Expertenwissens mit linguistischen Begriffen, durch die der Fuzzy-Controller mehr oder weniger mit empirischer Methodik optimal an einen nichtlinearen Prozess mit mehreren Ein- und Ausgangsgrößen modelliert wird, ohne dass das mathematische Modell des Prozesses (Regelstrecke) vorliegt.
Vereinfacht ausgedrückt entspricht die Anwendung der Fuzzy-Logik der menschlichen Denkweise, Tendenzen des Verhaltens eines unbekannten Systems zu erkennen, vorauszusehen und dem ungewollten Verhalten entgegenzuwirken. Diese Handlungsweise wird in sogenannten „WENN-DANN-Steuerregeln“ einer Regelbasis festgelegt.
Verfahren der stetigen und unstetigen Regelung:
- Die Regelung der Raumtemperatur des Referenzraumes kann über einen stufenlosen Regler erfolgen, der auf ein stetig arbeitendes Mischventil (Dreiwegemischer) wirkt, das bei Wärmebedarf auf den Heizkessel zugreift. Diese Form der Regelung wird häufig in Mehrfamilien-Wohnhäusern eingesetzt.
- Die Regelung der Raumtemperatur des Referenzraumes kann über einen Zweipunktregler erfolgen.
- Diese kostenminimale Variante eignet sich besonders für den intermittierenden Betrieb für das zyklische Ein-Ausschalten des Brenners.
Unstetige Regelung[Bearbeiten | Quelltext bearbeiten]
Ein unstetiger Zweipunktregler ohne Hysterese hat Eigenschaften, die einer hohen Kreisverstärkung entsprechen. Ob sie voll genutzt werden kann, hängt von der Art der Regelstrecke ab. Dieser Regler eignet sich besonders für Regelstrecken, die in weiten Grenzen zur kontinuierlichen Leistungsanpassung im intermittierenden Betrieb (Ein- und Ausschaltbetrieb) gesteuert werden müssen.
Das Verhältnis des maximalen zum augenblicklichen Wärmeenergiebedarf ist durch das Verhältnis der Einschalt- und Ausschaltzeit gegeben:
Die Stellgröße des Zweipunktreglers bestimmt in Abhängigkeit von der Regelabweichung das Verhältnis der Ein- zur Ausschaltzeit. Die Reglerhysterese und Totzeitverhalten der Regelstrecke setzen die Schaltfrequenz herunter. Spezielle Rückführungen des Zweipunktreglers und Aufschaltung eines D-Anteils der Regelabweichung erhöhen die Schaltfrequenz.
Berechnung der Wärmeenergieflüsse
Das Verhalten der Wärmeenergieflüsse kann berechnet werden, indem durch ein Blockdiagramm mit einzelnen Funktionsblöcken das dynamische Zeitverhalten der Wärmeenergieflüsse an den sogenannten Grenzflächen (z. B. Brenner / Heizkessel, Heizkörper / Luft oder Innenwände / Außenwände / Außenwitterung) dargestellt wird. Die Funktionsblöcke entsprechen geeigneten mathematischen Modellen als System-Beschreibungsfunktionen.
Tag- und Nachtabsenkung der Raumtemperatur
Für die zur Energie-Einsparung mit Hilfe der sogenannten Tag-Nacht-Absenkung der Raumtemperatur ist das Speicherverhalten der Gebäudewände und deren Dämmung von entscheidender Bedeutung. Bei konstanter niedriger Außentemperatur und längerfristiger Raumtemperaturabsenkung ist das Energie-Sparpotential groß. Bei kurzfristiger Raumtemperaturabsenkung müssen anschließend die Gebäudewände wieder aufgeheizt werden, ohne dass sich ein stationärer Temperaturzustand der Grenzflächen im Mauerwerk mit der Dämmung gebildet hat, der das Energiesparen möglich macht.[10]
Außengeführte Vorlauftemperaturbegrenzung[Bearbeiten | Quelltext bearbeiten]
Der Wärmebedarf in Wohnräumen ist im sehr kalten Winter ein Mehrfaches höher als in der Übergangszeit Herbst und Frühjahr. Deshalb wird die Vorlauftemperatur des Heizkreises mittels einer Vorsteuerung über einen Regler in Abhängigkeit von der Außentemperatur begrenzt, damit große Überschwingungen der Raumtemperatur (Regelgröße) aber auch Wärmeverluste vermieden werden.
Die Heizkörpertemperatur wird gewöhnlich nicht gemessen, sie wird aus dem Mittelwert der Vorlauftemperatur und der Rücklauftemperatur am Heizkessel erfasst. Wärmeverluste der isolierten Rohrleitungen werden vernachlässigt.
Die Kennlinie der Begrenzung der Vorlauftemperatur des Heizkreises als Funktion der Außentemperatur lässt sich bei kommerziellen Anlagen einstellen und ist abhängig von der Klimazone. Die begrenzte Vorlauftemperatur muss jeweils etwas höher liegen, als der Wert, der für den Wärmebedarf des eingestellten Referenzraum-Temperatursollwertes erforderlich ist. Die Begrenzungsregelung der Vorlauftemperatur als Funktion Außentemperatur kann durch einen einfachen Zweipunktregler erfolgen.
Störgrößen des Heizungsregelkreises[Bearbeiten | Quelltext bearbeiten]
Störgrößen der Raumtemperaturregelung sind Änderungen der Wärmeenergieerzeugung durch intermittierenden Betrieb, bei dem z. B. die Auswirkungen der Schwankungen des Gasdrucks (Gasheizkessel) oder Änderung des Brennheizwertes des Heizöles (Ölheizkessel) vernachlässigbar sind.
Kurzfristig angreifende Hauptstörgrößen auf die Raumtemperatur sind offenstehende Türen oder Fenster und die Sonneneinstrahlung im Fensterbereich.
Die Hauptstörgröße einer Gebäudeheizung ist der Einfluss der Außentemperatur. Die Änderung der Außentemperatur und der Einfluss von Wind und Niederschlägen sind wegen der Wärmespeicherfähigkeit der Gebäudemasse langfristig wirkende Störgrößen.
An Regelstrecken können Störgrößen an allen Teilregelstrecken angreifen. Kurzfristige Störgrößen zeichnen einen geringen Einfluss auf den Istwert der Regelgröße, wenn sie am Eingang der Regelstrecke auftreten. Den größten Einfluss haben Störgrößen an Regelstrecken, wenn sie am Ausgang der Regelstrecke auftreten.
Die Beurteilung eines linearen Regelkreises mit einem Führungsgrößensprung wird durch die Führungsgrößen-Übertragungsfunktion berechnet.
Die Beurteilung des Störverhaltens eines linearen Regelkreises an einer linearen Regelstrecke wird häufig durch einen Störsprung mit der Störgrößen-Übertragungsfunktion berechnet.
Stationäre oder sprungartige oder impulsartige Störgrößen im Regelkreis lassen sich in einem grafischen Signalflussplan durch eine Additionsstelle positiv oder negativ berücksichtigen.
Die dominanteste und in weiten Grenzen sich ändernde Störgröße der Regelstrecke einer Heizungsanlage ist der Wärmeenergie-Abfluss von der Raumtemperatur über die Gebäudewände zur Außenwitterung. Während der Einfluss einer Störgröße an einem beliebigen Regelkreis lediglich eine technische Information oder ein gefordertes bestimmtes Verhalten der Regelgröße anzeigt, bedeutet die Störgröße des Energieabflusses einer Gebäude-Temperaturregelung an die Außenwitterung ein Energie-Kostenfaktor erheblichen Ausmaßes.
Der Energieabfluss an die Außenwitterung ist unter normalen Betriebszuständen, d. h. geschlossene Fenster und Türen, abhängig:
- von der Außenwitterung, wie Außentemperatur, Sonne, Wind und Regen,
- von der Güte der Wärmedämmung des Gebäudes.
- Je besser die Außendämmung, umso niedriger kann die Heizkörpertemperatur für eine gegebene Außentemperatur sein.
- von der Größe der Referenzraum-Temperatur
- Jedes reduziertes Grad Celsius einer individuellen „Wohlfühl-Raumtemperatur“ reduziert die Heizkörpertemperatur prozentual beträchtlich.
- von der Größe der dominanten Zeitkonstanten der drei mathematischen Teilmodelle der Heizkörpertemperatur zur Raumtemperatur zur Außentemperatur.
- Für eine konstante Außenwitterung und einen gegebenen Sollwert der Referenzraum-Temperatur stellt sich nach genügend langer Zeit ein Gleichgewichtszustand zwischen der erzeugten Wärmeenergie und der über das Gebäude abfließenden Wärmeenergie ein.
Simulation eines Heizungsregelkreises mit Teilmodellen[Bearbeiten | Quelltext bearbeiten]

Aufgabenstellung: Berechnung des zeitlichen Verhaltens der mittleren Heizkörpertemperatur und der Raumtemperatur eines Referenzwohnraumes für die Raumtemperatur-Sollwertvorgabe von 5 °C auf 20 °C bei einer stationären Außentemperatur von −10 °C. Wind und Niederschläge sollen sich für diesen Vorgang nicht ändern.
Der Signalflussplan der Simulation der Referenzraum-Heizungsregelung zeigt die Beziehungen der Teilmodelle.
Datenvorgabe für den Heizungsregelkreis Für eine überschlägige Berechnung des Regelvorgangs der Raumtemperatur im Referenzraum müssen Vereinfachungen und Zahlenwerte-Annahmen aus Erfahrungen getroffen werden. Folgende Daten werden gegeben:
- maximale Vorlauftemperatur: 80 °C
- Sollwert Raumtemperatur: 20 °C
- stationäre Außentemperatur: −10 °C
- Abfluss der Wärmeenergie (in °C), wird empirisch gemessen:
- Für eine mittlere stationäre Heizkörpertemperatur von 60 °C und einer stationären Außentemperatur von −10 °C stellt sich nach genügend langer Zeit eine Raumtemperatur von 20 °C ein.
- Mit diesen Angaben entspricht eine Raumtemperatur-Änderung von 1 °C dem Verhältnis der Differenzwerte der Heizkörpertemperatur zur Raumtemperatur mit Bezug zur Außentemperatur:
- Faktor = [60 °C − (−10 °C)] / [20 °C − (−10 °C)] = 2,33 °C pro 1 °C Raumtemperaturänderung
- Begrenzte mittlere Heizkörpertemperatur bei −10 °C Außentemperatur: 70 °C
- Gewählter stationärer Anfangswert der Raumtemperatur im Frostschutzmodus als Sollwert: 5 °C
- Berechneter stationärer Anfangswert der mittleren Heizkörpertemperatur im Frostschutzmodus:
- Für eine geforderte stationäre Referenzraumtemperatur von z. B. 5 °C, d. h. Raumtemperaturabsenkung von 15 °C, ergibt sich eine geforderte Heizkörpertemperatur von:
- Heizkörpertemperatur = 60 °C − 2,33· 15 °C = 25 °C.
Definition der Teilmodelle anhand der geschätzten Datenvorgabe
Für den dynamischen Vorgang der Sollwert-Änderungen mit Bezug zur Heizkörpertemperatur, der Raumtemperatur und der Wärmeenergieabflüsse sind Anfangsbedingungen der Einzelsysteme zu berücksichtigen.
- Teilmodell 1: Wärmeenergieerzeugung vom Brenner zur Heizkörpertemperatur
- Die im Brenner und Heizkessel erzeugte Wärmeenergie wird mit der Heizungspumpe als Vorlauftemperatur durch alle Rohrleitungen und Heizkörper gepumpt und erscheint wieder am Heizkessel als Rücklauftemperatur. Die mittlere Heizkörpertemperatur wird als Mittelwert der Vor- und Rücklauftemperatur angenommen.
- Daten:
- Tt = 4 [Minuten], TE = 60 [Minuten] bei Anstieg, TE = 100 [Minuten] bei Abfall der Heizenergie:
- Teilmodell 2: Heizkörpertemperatur zur Raumtemperatur
- Die von den Heizkörpern abgegebene Wärmeenergie erwärmt die Raumluft, welche zunächst an den Fenstern und dann nach oben zur Zimmerdecke steigt und abkühlt. Dies führt über Konvektion und Strahlung zu Luftverwirbelungen, die auch nach einer Totzeit und Einschwingzeit den Raumtemperaturfühler erreichen.
- Die gemessene und geregelte Referenzraumtemperatur ist nicht identisch mit der Innenwand-Temperatur, des Fußbodens und Zimmerdecke des Referenzraumes, über die (stellvertretend für alle Räume) die Wärmeenergie zur Außenwitterung abfließt.
- Daten:
- Tt = 10 [Minuten], TE = 200 [Minuten] bei Anstieg, TE = 300 [Minuten] bei Abfall der Heizenergie:
- Teilmodell 3: Raumtemperatur zur Gebäudewand innen nach außen zur Außenwitterung
- Das mathematische Modell für die Wärmeenergie-Ableitung von der Raumluft über die Fenster und über die Gebäudewände zur Außendämmung und zur Außenwitterung ist sehr kompliziert und wird deshalb vereinfacht.
- Das Teilmodell 3 besteht aus einem statischen Teil, der die Beziehung Heizkörper-, Raum- und Außentemperatur über eine Geradengleichung wiedergibt, und einem dynamischen Teil, der die Speicherfähigkeit der Gebäudewände und -dämmung berücksichtigt.
- Je nach Beschaffenheit der Masse der Raumwände (Wärmespeicherfähigkeit, Wärmeleitfähigkeit, Innen-Wärmedämmung, Anteil Innen- und Außenwände) und des Dämmungsmaterials der Außenseite kann es sich um ein kompliziertes System höherer Ordnung mit großer dominanter Zeitkonstante handeln. Zur Vereinfachung dieses Teilmodels 3 wird als dynamisches Systemverhalten ein Verzögerungsglied 1. Ordnung (PT1-Glied) mit großer Ersatzzeitkonstante gewählt.
- Für die Simulation des Energieabflusses besteht mit diesen Angaben eine statische Beziehung, die durch eine Geradengleichung festgelegt werden kann.
- Vereinfachtes Modell des Zeitverhaltens:
- Geht man von einem linearen Zusammenhang der Heizkörpertemperatur zur gewählten Raumtemperatur bei konstanter Außentemperatur aus, so lässt sich für verschiedene Werte der Raumtemperatur die Größe der Heizkörpertemperatur aus Geradengleichungen errechnen.
- Allgemeine Geradengleichung mit X als Eingangsgröße und Y als Ausgangsgröße:
- Statische Beziehung von Teilmodell 3
- Über eine Geradengleichung wird bestimmt, welcher Wert von der gefilterten Heizkörpertemperatur (= Ausgang Modell 2) als Funktion der Außentemperatur subtrahiert werden muss, damit sich die Raumtemperatur als Regelgröße ergibt.
- Für die Raumtemperatur 20 °C ist die zugehörige Heizkörpertemperatur mit 60 °C gegeben. Für einen anderen Wert der Raumtemperatur kann die zugehörige Heizkörpertemperatur aus der Proportion der Temperaturdifferenzen zu −10 °C berechnet werden:
- Für das statische Modell 3 wird die Differenz [Heizkörpertemperatur – Raumtemperatur] benötigt. Dieser Wert wird von dem Ausgangssignal des Modells 2 subtrahiert:
- Damit ergeben sich die statische Werte für die Sollwertsprünge der Raumtemperatur die zugehörigen Werte der Heizkörpertemperatur und alle Zwischenwerte:
- Sollwert Raumtemperatur 20 °C:
- [Heizkörpertemperatur] – [Heizkörpertemperatur – Raumtemperatur] = [Raumtemperatur] = 60–40 = 20 °C
- Sollwert Raumtemperatur 5 °C:
- [Heizkörpertemperatur] – [Heizkörpertemperatur – Raumtemperatur] = [Raumtemperatur] = 25–20 = 5 °C
Grafische Darstellung der Temperaturwerte der Heizungsregelung[Bearbeiten | Quelltext bearbeiten]

Aufgabenstellung Anhand der Teilmodelle der Regelstrecke soll der grafische Verlauf der Heizkörpertemperatur und der Raumtemperatur vom Frostschutzmodus zum Betriebszustand berechnet und grafisch dargestellt werden.
- Für die Berechnung von Übertragungssystemen oder die Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekanntesten Programmen wie MATLAB und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.
- Alternativ können lineare Systeme numerisch mit Hilfe von Differenzengleichungen berechnet werden. Nichtlineare Systeme wie der Zweipunktregler lassen sich einfach mit Hilfe von WENN-DANN-SONST-Anweisungen berechnen. Eine Berechnungsfolge bezieht sich auf eine Kette von hintereinandergeschalteten Systemen, beginnend mit dem Eingangssignal und endend mit dem Ausgangssignal. Jede Folge k bezieht sich auf die diskrete Zeit k·Δt.
Zum besseren Verständnis werden zwei Diagramme mit dem statischen und dynamischen Verhalten von Teilmodell 3 dargestellt.
- Grafische Darstellung des zeitlichen Verhaltens der Temperaturwerte ohne Wärmespeicherung der Gebäudewände (Teilmodell 3 mit T = 0).
- Grafische Darstellung des zeitlichen Verhaltens der Temperaturwerte mit Wärmespeicherung der Gebäudewände (Teilmodell 3 mit T = 500 [Minuten]).
Kritische Beurteilung der Simulationsergebnisse
- Prinzipiell entsprechen die berechneten Zeitverläufe der Heizkörpertemperatur und der Raumtemperatur realistischen Heizungsregelungen.
- Zuverlässigkeit der mathematischen Modelle
- Die Simulation eines dynamischen Prozesses ist so gut wie die Güte der mathematischen Modelle der Regelstrecke.
- Modell 1 (Wärmeenergieerzeugung zum Heizkörper) kann weitgehend der Realität entsprechen.
- Modell 2 (Erwärmung der Raumtemperatur) ist physikalisch dem Modell 1 nachgeschaltet, kann aber nicht die Rückwirkungsfreiheit auf Modell 1 durch die größeren Zeitkonstanten garantieren. Es wirkt mehr als Tiefpassfilter 1. Ordnung auf die sägezahnförmige Änderung der Heizkörpertemperatur.
- Modell 3 (Abfluss der Wärmeenergie an die Außenwitterung) subtrahiert von der Ausgangsgröße des Modells 2 den Anteil der nach außen abfließenden Wärmeenergie. Obwohl es sich bei dem Modell 3 um ein System mit verteilten Energiespeichern handelt, wird es aus Gründen einfacher Berechenbarkeit als ein System mit einem konzentrierten Energiespeicher behandelt. Damit ergibt sich die Regelgröße Raumtemperatur als Funktion der Heizkörpertemperatur und der Außentemperatur.
- Die Zeitkonstanten aller Teilmodelle sind geschätzt.
Grafische Darstellungen der Temperaturwerte

Zum besseren Verständnis werden die Regelvorgänge in zwei Diagrammen, statisch ohne die gespeicherte Wärmeenergie der Wände und dynamisch mit gespeicherter Energie der Wände dargestellt. Es handelt sich um das dritte Teilmodell, dessen Zeitkonstante einmal auf einen Wert für T = 0 und T = 500 gesetzt wird.
Nachfolgend wird die Simulation des Modells des Regelkreises der Gebäudeheizung für einen Sprung des Sollwertes aus dem Frostschutzmodus 5 °C zum Betriebsmodus 20 °C dargestellt.
Kommentar zur Abbildung der Simulation mit dem dritten Teilmodell ohne Speicherfähigkeit der Raumwände Die Berechnung des Abflusses der Wärmeenergie von den Anfangswerten zu den Endwerten erfolgt rein statisch ohne gespeicherte Wärmeenergie der Gebäudewände.
Der Sollwertsprung erfolgt nach 200 Minuten. Das vereinfachte statische Teilmodell 3 als PT1-Glied mit dem Verhalten der Zeitkonstante T = 0 zeigt die stationären Zustände der Heizkörpertemperatur und der Raumtemperatur an, die sich nach genügend langer Zeit einstellen. Der Übergang von den unteren Temperaturwerten zu den oberen Temperaturwerten ist zeitlich nicht real, weil zu jedem Wert der Heizkörpertemperatur und der Raumtemperatur nicht die gespeicherte Wärme der Gebäudewände berücksichtigt ist.
Kommentar zur Abbildung der Simulation mit dem dritten Teilmodell mit Speicherfähigkeit der Raumwände Die Berechnung des Abflusses der Wärmeenergie von den Anfangswerten zu den Endwerten erfolgt mit Berücksichtigung der gespeicherten Wärmeenergie der Gebäudewände.
Der Sollwertsprung erfolgt nach 200 Minuten. Das vereinfachte statische Teilmodell 3 als PT1-Glied für die Wärmespeicherfähigkeit der Raumwände mit der Zeitkonstante T = 500 Minuten zeigt das Verhalten des Anstiegs der Heizkörpertemperatur und der Raumtemperatur an. Dabei wird deutlich, dass die Raumtemperatur den Sollwert 20 °C bereits erreicht hat, während die Heizkörpertemperatur wegen der gespeicherten Wärmeenergie der Wände nur mit 45 °C gefordert wird. Erst nach ca. 2000 Minuten stellt sich die Heizkörpertemperatur von 60 °C als statisch ein, konstante Witterungseinflüsse vorausgesetzt.
Mathematische Methoden zur Beschreibung und Berechnung eines Regelkreises[Bearbeiten | Quelltext bearbeiten]
Dieses Kapitel zeigt die Anwendung der Methoden der Regelungstechnik und der Systemtheorie für die Berechnung von dynamischen Systemen und Regelkreisen. Dabei werden die Begriffe von Verfahren der Systembeschreibungen, Übertragungsfunktionen, lineare und nichtlineare Regelstrecken, zeitinvariante und zeitvariante Systeme, Zweipunktregler, mathematische Systemmodelle und numerische Berechnungen tangiert und Hilfen auf ausführliche Artikel bzw. deren Kapitel gegeben.
Ein dynamisches System ist eine Funktionseinheit mit einem bestimmten Zeitverhalten und hat mindestens einen Signaleingang und einen Signalausgang. Modelle (Modellbildung) eines realen dynamischen Übertragungssystems werden mathematisch beschrieben durch:
- Übertragungsfunktion und Frequenzgang
- Zustandsraumdarstellung
- Differenzengleichung (Differenzenverfahren), Numerische Berechnung linearer dynamischer Systeme. Tangiert auch nichtlinearer Systeme (Logische Befehle, Tabellenwerte).
Gewöhnliche Differentialgleichungen[Bearbeiten | Quelltext bearbeiten]
Eine Differentialgleichung (kurz DGL) ist eine Gleichung, die eine oder mehrere Ableitungen einer unbekannten Funktion enthält.[11] Verschiedene physikalische Probleme lassen sich mit DGL-en formal identisch darstellen.
Kommen Ableitungen nur bezüglich einer Variablen vor, spricht man von einer „gewöhnlichen Differentialgleichung“, wobei der Begriff „gewöhnlich“ bedeutet, dass die betrachtete Funktion nur von einer Veränderlichen abhängt. Mit gewöhnlichen DGL-en lassen sich viele dynamische Systeme aus Technik, Natur und Gesellschaft beschreiben.
Eine lineare DGL enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Es treten keine Produkte der gesuchten Funktion und ihrer Ableitungen auf; ebenso erscheint die gesuchte Funktion nicht in Argumenten von Winkelfunktionen, Logarithmen usw.
Entstehung einer Differentialgleichung Eine DGL ist eine Bestimmungsgleichung für eine unbekannte Funktion. Die Lösung einer DGL ist keine Zahl, sondern eine Funktion!

Beispiel elektrischer Schwingkreis: Spannungsbilanz: Nach dem 2. Kirchhoffschen Satz ist Summe aller Spannungen einer Masche gleich Null.
Der Spannungsabfall am Widerstand R ergibt sich zu UR = i · R. Nach dem Induktionsgesetz ist die Spannung an der Induktivität UL = L · di / dt. Der Ladestrom am Kondensator ist proportional der Spannungsänderung am Kondensator i(t) = C · dy / dt.
Die Anwendung des Maschensatzes führt zunächst zu einer Differenzialgleichung 1. Ordnung:
Setzt man in die DGL für i(t):
ein, dann ergibt sich die Schwingungsgleichung:
Es können Zeitkonstanten wie T1 = R · C und T2² = L · C eingeführt werden. Ersetzt man auch die in der Systembeschreibung übliche Darstellung der Eingangsgröße und Ausgangsgröße , dann lautet die bekannte DGL für einen Reihenschwingkreis:
Grundlagen der Übertragungsfunktion als Systembeschreibung[Bearbeiten | Quelltext bearbeiten]

Die am häufigsten dargestellte Systembeschreibung linearer zeitinvarianter Systeme ist die Übertragungsfunktion mit der komplexen Frequenz . Sie wird erfolgreich eingesetzt für Systemanalyse, Systemsynthese, Systemstabilität und erlaubt die algebraische Behandlung von beliebig geschalteten rückwirkungsfreien Teilsystemen.
Eine Übertragungsfunktion beschreibt die Abhängigkeit des Ausgangssignals eines linearen, zeitinvarianten Systems (LZI-System) von dessen Eingangssignal im Bildbereich (Frequenzbereich, s-Bereich). Sie wird definiert als Quotient der Laplace-transformierten Ausgangsgröße zur transformierten Eingangsgröße :
Die Laplace-Transformation ist eine Integraltransformation, mit deren Anwendung sich eine Zeitfunktion in eine Bildfunktion mit der komplexen Frequenz übertragen lässt. Die Bildfunktion lässt sich mit verschiedenen mathematischen Methoden wieder als eine Zeitfunktion darstellen.
Dynamische zeitinvariante Systeme mit konzentrierten Energiespeichern (z. B. Feder-Masse-Dämpfer-Systeme oder elektrische L-, C- und R-Glieder) werden durch gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten beschrieben. Wenn sich das System im Ruhezustand befindet, haben die Energiespeicher den Wert Null.
Zur Vereinfachung der Berechnung und zum leichteren Verständnis wird die Differenzialgleichung einer Laplace-Transformation unterzogen. Dabei wird nach dem Laplace-Differentiationssatz eine Ableitung 1. Ordnung der Differenzialgleichung durch die Laplace-Variable s als komplexe Frequenz ersetzt. Höhere Ableitungen n-ter Ordnung werden durch ersetzt.
Das Ausgangs-/Eingangsverhalten dynamischer Systeme, die durch DGL-en beschrieben werden können, ist in den meisten Fällen nichtlinear und kann daher auch nicht durch Übertragungsfunktionen G(s) beschrieben werden. Man beschränkt sich annäherungsweise auf den Arbeitspunkt des untersuchten Systems und gewinnt damit eine Linearisierung der DGL. Damit entsteht eine lineare DGL mit konstanten Koeffizienten.
Beispiel einer gewöhnlichen Differenzialgleichung mit konstanten Koeffizienten:
Die Laplace-Transformierte der Differenzialgleichung lautet:
Die Koeffizienten a und b der Differenzialgleichung sind mit denen der Übertragungsfunktion identisch.
Das Ergebnis der Transformation wird nach Ordnung der Terme des sich ergebenden Polynoms als Verhältnis der Ausgangsgröße zur Eingangsgröße als Übertragungsfunktion definiert. Die Übertragungsfunktion G(s) kann immer als gebrochen-rationale Funktion geschrieben werden. Da die Übertragungsfunktion zur Beschreibung des Eingangs- und Ausgangsverhaltens verwendet wird, soll das Übertragungssystem für eine gegebene Eingangsgröße zu einem betrachteten Zeitpunkt eine Ausgangsgröße gleich Null aufweisen.
Faktorisierung der Übertragungsfunktion im s-Bereich[Bearbeiten | Quelltext bearbeiten]
Mittels der Nullstellenbestimmung können die Polynome der Übertragungsfunktion in eine Produktform (Linearfaktoren) im Zähler und Nenner gebracht werden. Die Pole (Nullstellen des Nenners) oder Nullstellen (Nullstellen des Zählers) sind entweder Null, reell oder konjugiert komplex. Die Produktdarstellung im Zähler und Nenner der Übertragungsfunktion ist mathematisch identisch mit der Polynomdarstellung.
Die Pole und Nullstellen der Übertragungsfunktion sind die wichtigsten Kenngrößen des Systemverhaltens.
Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
Linearfaktoren:
- Bei Linearfaktoren 1. Ordnung sind die Nullstellen oder Pole reelle Zahlenwerte. Stabile Systeme enthalten negative Realteile.
- Linearfaktoren 2. Grades mit konjugiert komplexen Nullstellen oder Polen werden zur einfacheren Berechenbarkeit zu quadratischem Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.
- Linearfaktoren werden meist in die Zeitkonstanten-Darstellung durch Reziprokbildung der Nullstellen und Pole umgerechnet.
- Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Nullstelle :
In der linearen Regelungstechnik ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (phasenminimalen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf folgende drei Grundformen (Linearfaktoren) geschrieben bzw. zurückgeführt werden können. Sie haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler (differenzierendes Verhalten) oder im Nenner (verzögernd, Integrierend) einer Übertragungsfunktion stehen.
In Abhängigkeit von den Zahlenwerten der Koeffizienten und der Polynom-Darstellung können die Produkte folgende drei Formen in der Zeitkonstanten-Darstellung annehmen:
Typ Linearfaktor Bedeutung im Zähler Bedeutung im Nenner
(Nullstelle = 0)Differenzierer, D-Glied Integrator, I-Glied
(Nullstelle reell)PD-Glied Verzögerung, PT1-Glied
(Nullstellen konjugiert komplex)PD2-Glied: für 0 < D < 1 Schwingungsglied PT2-Glied: für 0 < D < 1
- Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.
Die Übertragungsfunktion eines dynamischen Übertragungssystems kann einfache und mehrfache Linearfaktoren im Zähler und Nenner enthalten.
Definition der Variablen s[Bearbeiten | Quelltext bearbeiten]
- ist die unabhängige Variable im komplexen Frequenzbereich (Bildbereich, s-Bereich) mit als Realteil und als Imaginärteil. Sie erlaubt beliebige algebraische Operationen im s-Bereich, ist aber nur ein Symbol für eine vollzogene Laplace-Transformation und enthält keinen Zahlenwert. Exponenten von entsprechen dem Grad der Ableitung der Differentiale.
- Zahlenwerte entstehen aus den Koeffizienten und der Polynomdarstellung, indem die Polynome der Übertragungsfunktion durch Nullstellenzerlegung in Linearfaktoren (Produkte) zerlegt werden. Diese Nullstellen bzw. Pole können Null, reell oder konjugiert komplex sein.
- Die Realteile und die Imaginärteile der Nullstellen oder Pole können in Abhängigkeit von den Zahlenwerten der Koeffizienten und auch den Zahlenwert Null aufweisen. Damit entstehen die drei Formen der Linearfaktoren z. B. im Nenner der Übertragungsfunktion mit dem Verhalten Integration, Verzögerung, Verzögerung 2. Ordnung konjugiert komplex.
Tabelle sämtlicher vorkommenden Arten der regulären Übertragungsfunktionen in Zeitkonstanten-Darstellung:
Benennung → P-Glied I-Glied D-Glied PD1-Glied PT1-Glied PT2-Glied (Schwingungsglied) PD2-Glied Totzeitglied Übertragungsfunktion G(s) Pole und Nullstellen keine keine Übergangsfunktion
(Sprungantwort)




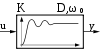
grafisch nicht darstellbar 
Anmerkungen zur Übertragungsfunktion[Bearbeiten | Quelltext bearbeiten]
- Der große Vorteil der Beschreibung linearer dynamischer Systeme als Übertragungsfunktionen mit den Linearfaktoren besteht darin, dass nur sechs leicht einzuprägende Grundformen des Systemverhaltens existieren, die sich zu größeren Systemformen zusammensetzen können. Die transzendente Form des nichtlinearen Totzeitgliedes gehört nicht dazu, es sei denn, es wird als gebrochen-rationale Funktion dem Verhalten des Totzeitgliedes angenähert.
- Auch im Zusammenhang mit anderen Systembeschreibungen wie die Differentialgleichung, Differenzengleichung, Zustandsraumdarstellung und gemischten linearen und nichtlinearen Modellen ist die Benennung von Übertragungssystemen als Übertragungsfunktion von Vorteil, weil der Bekanntheitsgrad der Systemfunktion so hoch ist.
- Die Übertragungsfunktionen können beliebig als einzelne Übertragungssysteme in der Reihen- und Parallelschaltung eines Blockdiagramms zusammengefasst und algebraisch behandelt werden.
- Die Verstärkungsfaktoren des -Gliedes und des -Gliedes können auch als Zeitkonstanten geschrieben werden: .
- Die dargestellten Übertragungsfunktionen mit -Anteilen werden als „ideal“ bezeichnet. Diese Systeme lassen sich „real“ nicht ohne Kombination mit einem Verzögerungsglied (-Glied) herstellen. Dabei muss die Zeitkonstante des Verzögerungsgliedes wesentlich kleiner sein, als die des D-Anteils.
- Beispiel reales -Glied mit TV ≫ T:
- Die numerische Berechnung von idealen -Anteilen funktioniert mit Hilfe der Differenzengleichungen problemlos. Es können bei der Differentiation keine unendlich großen Flanken entstehen, weil über die Zeit gerechnet wird.
- Fazit: Bei der numerische Berechnung kompensiert ein ideales -Glied ein -Glied bei gleichen Zeitkonstanten vollständig zum Faktor .
- Die differenzierende Form der Übertragungsfunktion 2. Ordnung (-Glied) mit konjugiert komplexen Nullstellen erlaubt bei gleichen Zeitkonstanten und gleichem Dämpfungsgrad die Kompensation des Verzögerungsgliedes 2. Ordnung mit konjugiert komplexen Polen.
- Anwendung: Vorfilter im Regelkreiseingang reduziert gedämpfte Schwingungen der Regelgröße und erlaubt damit eine höhere Kreisverstärkung.
- Die Übertragungsfunktionen werden immer als gebrochen-rationale Funktionen geschrieben.
- Der Übertragungsfunktion eines Systems kann die transzendente Funktion des Totzeitgliedes multiplikativ angehängt werden zu . Diese Form der Übertragungsfunktion als Gesamtsystem ist nur für Frequenzgang-Analysen geeignet. Beliebige algebraische Operationen mit einem Totzeitglied sind nicht erlaubt.
- Nichtreguläre Übertragungsfunktionen enthalten ein Minuszeichen in der Gleichung (= positive Nullstelle). Sie können durch eine positive Rückkopplung (= Mitkopplung) entstehen und verhalten sich monoton instabil. Durch eine beliebige Eingangserregung strebt die Ausgangsgröße eines instabilen -Gliedes in Abhängigkeit von der Zeitkonstante bis zu seiner natürlichen Begrenzung einen unendlich großen Wert an.
Beispiel der Schreibweise eines Verzögerungsgliedes 1. Ordnung mit dem Verstärkungsfaktor :
Diese Art Gleichungen der Übertragungsfunktionen lassen sich algebraisch behandeln, gelten für lineare Systeme und beziehen sich auf zeitinvariantes Verhalten. Übertragungsfunktionen können mit beliebigen Linearfaktoren zu Regelstrecken und Regelkreisen algebraisch zusammengesetzt werden, solange kein Totzeitsystem enthalten ist. Ist ein Eingangssignal als Testsignale gegeben, kann mittels Laplace-Transformationstabellen das Zeitverhalten des Ausgangssignals errechnet werden.
Übertragungsfunktionen als Blockstruktur im Signalflussplan[Bearbeiten | Quelltext bearbeiten]
Übertragungssysteme können aus Teilsystemen als Blöcke zusammengefasst werden. Es gilt das Superpositionsprinzip. Die Systeme in Produktdarstellung können in der Reihenfolge beliebig verschoben werden. Die Systemausgänge dürfen nicht durch nachfolgende Systemeingänge belastet werden (Rückwirkungsfreiheit).
- Parallelschaltung:
- Gleichung der Übertragungsfunktion der Parallelschaltung:
- Reihenschaltung:
- Gleichung der Übertragungsfunktion der Reihenschaltung:
- Gegenkopplung oder Rückkopplung:
- Gleichung der Übertragungsfunktion der Gegenkopplung:
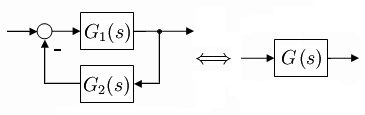
- Bei einem Regelkreis, der in dem Gegenkopplungszweig kein statisches oder dynamisches Teilsystem enthält, wird das System G2(s) = 1.

- Damit lautet die Übertragungsfunktion des geschlossenen Regelkreises:
- Eine Mitkopplung ist eine positive additiv wirkende Rückführung des Signalausgangs auf den System-Eingang. Sie führt je nach Größe der Verstärkung von G1(s) zur monotonen Instabilität oder zu einem Hysterese-Effekt.
- Gleichung der Übertragungsfunktion der Mitkopplung:
- Mit G1(s) als offener Regelkreis werden beliebige algebraische Zusammenführungen der Teilsysteme des Reglers und der Regelstrecke verstanden.
Lineare Regelstrecken[Bearbeiten | Quelltext bearbeiten]
Lineare Systeme sind dadurch gekennzeichnet, dass der sogenannte Überlagerungssatz und der Verstärkungssatz gelten. Der Überlagerungssatz sagt aus, dass, wenn das System mit den Zeitfunktionen f1(t) und f2(t) gleichzeitig erregt wird, auch die Systemantwort aus einer Überlagerung der Systemantwort von f1(t) und der Systemantwort von f2(t) gebildet wird.
Das Verstärkungsprinzip bedeutet, dass bei doppelter Amplitude der Eingangsfunktion die Systemantwort ebenso doppelt so groß ist.
Natürliche lineare Regelstrecken enthalten oft verzögernde, integrierende und mit Totzeit behaftete Teilsysteme.
Ein elektrischer Widerstands-Kondensator Tiefpass 1. Ordnung im rückwirkungsfreien Zustand mit der Zeitkonstante T = R·C wird durch folgende Übertragungsfunktion beschrieben:
Verzögerungsgliedes 1. Ordnung (PT1-Glied):
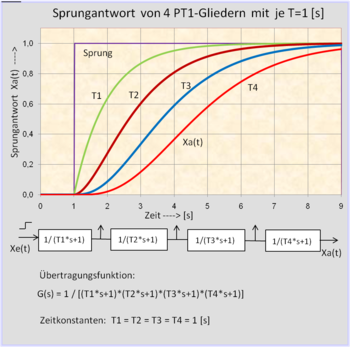
Für die Berechnung des Zeitverhaltens von Übertragungssystemen G(s) mit der Übertragungsfunktion müssen die Eingangssignale (Testsignale) im s-Bereich definiert werden.
Für die Berechnung der Sprungantwort eines Systems im Zeitbereich lautet der normierte Sprung 1(t) als Laplace-transformiertes Test-Eingangssignal U(s) = 1 / s.
Die Gleichung zur Berechnung des Zeitverhaltens des PT1-Gliedes kann direkt aus den Laplace-Transformations-Tabellen abgelesen werden:
Gesuchte Funktion im s-Bereich:
Zugehörige Funktion im Zeitbereich:
Der Faktor K unterliegt nicht der Transformation und ist deshalb im s-Bereich wie auch im Zeitbereich gültig.
Wird die korrespondierende Zeitfunktion einer Übertragungsfunktion in Zeitkonstanten- oder Nullstellen-Darstellung in den Transformationstafeln ohne das Laplace-transformierte Eingangssignal gesucht, ist das Ergebnis immer die Impulsantwort des Systems.
Lineare Regelstreckenarten
Die Zeitkonstante T besagt für ein Verzögerungsglied 1. Ordnung, dass ein Ausgangssignal nach einem Sprung eines Eingangssignals ca. 63 % des Wertes des Eingangssignals erreicht hat und sich der Signalverlauf asymptotisch – nach ca. 5 Zeitkonstanten – an den Maximalwert des Eingangssignal annähert.
- Ein Verzögerungsglied 1. Ordnung (PT1-Glied) verhält sich zeitinvariant, wenn für ein ansteigendes (Sprung) oder abfallendes (Rücksprung) Eingangssignal u(t) das Zeitverhalten (Zeitkonstante) sich nicht ändert. Dies erklärt sich aus der zugehörigen gewöhnlichen Differenzialgleichung mit konstanten Koeffizienten.
- Ein Verzögerungsglied 2. Ordnung mit konjugiert komplexen Polen, z. B. ein gedämpftes Feder-Masse-System, wird als Schwingungsglied bezeichnet. Die Sprungantwort nähert sich je nach Dämpfungsgrad D mit ausklingender Schwingung dem maximalen Wert der Eingangsgröße an.
- Eine Regelstrecke mit mehreren PT1-Gliedern bezeichnet man als Regelstrecke mit Ausgleich, auch als globales (proportionales) P-Verhalten.
- Eine Regelstrecke mit mehreren PT1-Gliedern und einem I-Glied bezeichnet man als Regelstrecke mit globalem I-Verhalten.
- Eine totzeitbehaftete Regelstrecke mit Verzögerungsgliedern kann nicht beliebig algebraisch berechnet werden. Es sei denn, die Totzeit wird annäherungsweise als gebrochen-rationale Funktion mit Verzögerungsgliedern definiert.
Vorteil der Systembeschreibung mit Übertragungsfunktionen (ohne Totzeitverhalten)
- Einfache algebraischen Berechnung beliebiger Systemverknüpfungen aller Einzelsysteme möglich
- Regelkreisglieder des Reglers und der Regelstrecke der offenen Kreises können zu einem Regelkreis geschlossen werden. Die sich daraus ergebenden Polynome können in Pole und Nullstellen zerlegt werden und wieder als faktorielle Grundglieder (Linearfaktoren) meist in Zeitkonstanten-Darstellung geschrieben werden.
- Sämtliche Systemeigenschaften lassen sich aus der Pol-Nullstellendarstellung ablesen.
- Mit den grafischen Methoden „Ortskurve des Frequenzgangs“ und dem „Stabilitätskriterium von Nyquist“ lässt die Stabilität des geschlossenen Regelkreises anhand der Einzelsysteme G(s) des offenen (aufgeschnittenen) Regelkreises bestimmen.
- Für ein bekanntes Laplace-transformiertes Test-Eingangssignal wie die Sprung- oder Stoßfunktion kann über die Anwendung von Laplace-Transformationstabellen das Zeitverhalten eines Einzelsystems oder eines Regelkreises berechnet und grafisch dargestellt werden.
- Reglerentwurf
- Regelstrecken können vereinfacht werden, wenn durch PD1-Glieder des Reglers Verzögerungsglieder (PT1-Glieder) kompensiert werden.
Übertragungsfunktion und Frequenzgang[Bearbeiten | Quelltext bearbeiten]
Die Übertragungsfunktion ist eine nicht messbare Funktion des Verhältnisses der Laplace-transformierten Ausgangsgröße zur Eingangsgröße. Sie kann jederzeit in den Frequenzgang bei identischen Koeffizienten (Zeitkonstanten) überführt werden.
Der Frequenzgang ist ein Spezialfall der Übertragungsfunktion.
Im Gegensatz zur Übertragungsfunktion kann der Frequenzgang eines linearen Übertragungssystems gemessen werden, indem ein sinusförmiges Eingangssignal konstanter Amplitude mit variabler Frequenz das unbekannte System erregt und die Ausgangsgröße aufgezeichnet wird. Die Entstehungsgeschichten des Frequenzgangs und der Übertragungsfunktion sind unterschiedlich, die Schreibweisen können identisch bleiben.
Mit den grafischen Methoden „Ortskurve des Frequenzgangs“ und dem „Stabilitätskriterium von Nyquist“ kann auch das Totzeitverhalten eines Teilsystems behandelt werden, weil diese Verfahren sich auf den offenen Regelkreis beziehen.

Zeitinvariante und zeitvariante Regelstreckenkomponenten[Bearbeiten | Quelltext bearbeiten]
Beispiel Gebäudeheizung: In einem geheizten Gebäude fließt der erzeugte Wärmestrom vom Heizkörper über die Raumluft zu den Gebäudewänden über die Dämmungen an die Außenwitterung. Die verschiedenen Wärmeströme zwischen den Massen und zugehörigen Dämmungen haben je ein bestimmtes Zeitverhalten, das für eine Analyse der gesamten Regelstrecke zu definieren ist.
Zeitinvarianz
Bei den bisher dargestellten dynamischen Systemen handelt es sich um zeitinvariante Systeme mit konzentrierten Energiespeichern.
Ein dynamisches Übertragungssystem ist zeitinvariant, wenn es sich über die Zeit nicht ändert, d. h., die Systemantwort auf ein identisches Eingangssignal ist von unabhängig. Die Koeffizienten der mathematischen Systembeschreibung sind konstant (zeitlich unveränderlich, invariant).
Ein zeitinvariantes Verzögerungsglied (PT1-Glied) verhält sich für einen Signaleingangssprung wie auch für den Signalrücksprung identisch, d. h., es strebt immer asymptotisch beim Ansprung den Maximalwert oder beim Rücksprung den Anfangswert mit gleicher Zeitkonstante an.
Zeitvarianz
Für die Beschreibung eines dynamischen Systems z. B. bei einem Wärmestrom in einem homogenen Materialstoff (Wasser, Luft, Stein) handelt es sich um ein System mit räumlich verteilten Energiespeichern.
Ein zeitvariantes System verhält sich zu verschiedenen Zeitpunkten unterschiedlich. Bei technischen Systemen liegt der Grund dafür meist in zeitabhängigen Parameterwerten, zum Beispiel durch Änderung der Koeffizienten der Energiespeicher [zeitabhängige Koeffizienten der Ableitungen ].
Bei vielen Prozessen sind die Auswirkungen der Zeitvarianz so klein oder langsam, dass diese Systeme näherungsweise als zeitinvariant behandelt werden können.
Die den Übertragungsfunktionen zugehörigen gewöhnlichen Differenzialgleichungen haben konstante Koeffizienten. Konstante Koeffizienten bedeuten, dass sich das Zeitverhalten des Systems nicht ändert. Wird z. B. das Zeitverhalten einer beschleunigten Masse beschrieben und es handelt sich um eine beschleunigte Rakete, die ihre Masse ändert, so handelt es sich um einen zeitvarianten Vorgang.

Mathematisches zeitvariantes Modell des Wärmeflusses in einem homogenen Medium z. B. Luft
Das Übertragungsverhalten eines Signalsprungs in einem räumlichen homogenen Medium (Materialstoff) zeigt sich in seinem zeitlichen Verhalten zwischen zwei Messpunkten angenähert als Verzögerungsglied 1. Ordnung mit einer Totzeit und unterschiedlichen Zeitkonstanten.
Das mathematische Modell für den Wärmefluss in einem homogenen Medium lässt sich nach der Aufzeichnung der Sprungantwort durch ein einfaches Modell mit einem PT1-Glied und einem Totzeitglied annähern. Die Parameter der Ersatztotzeit und der Ersatzzeitkonstanten können anhand eines aufzuzeichnenden Messprotokolls experimentell bestimmt werden.
Für eine Gebäudeheizung wird berücksichtigt, dass die Aufheizung des Kessels schnell und die Abkühlung wegen der Wärmedämmungen langsam erfolgt. Das Gleiche gilt für den Energieabfluss vom Heizkörper an die Raumluft und über die Wände an die Außenwitterung. Solche Systeme verhalten sich zeitvariant, d. h., für einen Signalsprung hat das System eine andere Zeitkonstante als für einen Signal-Rücksprung. Je besser die Dämmung eines aufgeheizten Mediums ist, umso unterschiedlicher sind die Zeitkonstanten für die Aufheizung (klein) und der Wärmeabfluss (groß).
Falls die Darstellung der Totzeit mit dem Rechenprogramm Probleme bereitet, kann die dargestellte Modellgleichung auch praktisch identisch durch eine sehr gute Annäherung mit Ersatztotzeiten durch z. B. n = 3 PT1-Glieder wie folgt dargestellt werden:
Nichtlineares Übertragungssystem[Bearbeiten | Quelltext bearbeiten]
Es handelt sich bei diesem Abschnitt um nichtlineares Systemverhalten, dass nicht durch DGL-en beschrieben werden kann.
Die lineare Systemeigenschaft ist häufig nicht gegeben, da viele zusammenwirkende Systeme z. B. in der Regelungstechnik bei Ventil-Kennlinien, Stellgrößenbegrenzungen oder Schaltvorgängen keine Linearität aufweisen.

Ein nichtlineares System kann entweder in Form nichtlinearer statischer Kennlinien oder in Form nichtlinearer Operationen wie Multiplikation oder Division von Variablen in algebraischen Gleichungen und Differentialgleichungen auftreten.
Ein nichtlineares dynamisches System 2. Ordnung entsteht beispielsweise durch ein Feder-Masse-Dämpfer-System, wenn das Federsystem oder der Dämpfer ein nichtlineares Verhalten hat. Anhand der Vielzahl der Formen nichtlinearer Systeme ist es schwierig, diese in bestimmte Klassen einzuordnen. Nichtlineare Systeme kann man als einzigartig einstufen.
Bei nichtlinearen Übertragungssystemen wirkt mindestens eine nichtlineare Funktion in Verbindung mit linearen Systemen. Diese nichtlinearen Funktionen werden nach stetigen und unstetigen Nichtlinearitäten unterschieden. Stetige Nichtlinearitäten weisen keine Sprünge der Übertragungskennlinie auf wie z. B. bei quadratischem Verhalten. Unstetige Übertragungskennlinien wie bei Begrenzungen, Hysterese, Ansprechempfindlichkeit, Zwei- und Mehrpunkt-Charakter haben keinen kontinuierlichen Verlauf.
Das Prinzip der Superposition gilt nicht bei nichtlinearen Übertragungssystemen.
Folgende Beziehungen ergeben sich bei nichtlinearen Systemen:
- Wird ein nichtlineares Übertragungssystem in einem festen Arbeitspunkt betrieben, dann kann das nichtlineare Verhalten des Systems durch ein lineares Modell für die nähere Umgebung des Arbeitspunktes ersetzt werden.
- Jeder nichtlineare Zusammenhang kann im Kleinsignalverhalten näherungsweise linear beschrieben werden. Die Näherung wird umso besser, je kleiner der Differenzenquotient zu am Arbeitspunkt ist.
- Ist eine nichtlineare Funktion als grafische Kennlinie gegeben, dann kann durch Anlegen einer Tangente im gewünschten Arbeitspunkt die Steigung der Tangente für die linearisierte Beziehung bestimmt werden
- Ein nichtlineares dynamisches System mit kontinuierlich fallender oder steigender Kennlinie kann auch durch Einbindung in einen eigenen Regelkreis linearisiert und damit auch in seinem dynamischen Verhalten verbessert werden.
- Nichtlineare Differenzialgleichungen lassen sich meist nur numerisch lösen. Wenn ein Übertragungssystem in Teilsysteme zerlegt werden kann und das nichtlineare Verhalten einzelner Systeme als analytische Gleichung oder Wertetabelle vorliegt, kann relativ einfach das Verhalten eines nichtlinearen dynamischen Systems berechnet werden.
- Das Zusammenwirken von unstetigen, nichtlinearen, statischen Systemen mit linearen Systemen zu Regelkreisen kann mit dem grafischen Verfahren der Harmonischen Balance optimiert werden. Die Anwendung der Harmonischen Balance zur Analyse von nichtlinearen Regelkreisen mit dem anschaulichen Zwei-Ortskurven-Verfahren zeigt, wann Dauerschwingungen auftreten und wie sich Dauerschwingungen vermeiden lassen.
- Flachheitsbasierte Systeme
- Flachheit in der Systemtheorie ist eine Systemeigenschaft, die den Begriff der Steuerbarkeit linearer Systeme auf nichtlineare Systeme ausweitet. Ein System, das die Flachheitseigenschaft besitzt, heißt flaches System.
- Die Flachheitseigenschaft ist für die Analyse und Synthese nichtlinearer dynamischer Systeme nützlich. Sie ist besonders vorteilhaft für die Trajektorienplanung und asymptotische Folgeregelung nichtlinearer Systeme.
Grundlagen der numerischen Berechnung von dynamischen Übertragungssystemen[Bearbeiten | Quelltext bearbeiten]
Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Mit handelsüblichen Personal-Computern kann das Verhalten beliebig vermaschter Systemstrukturen mittels numerischer Berechnung relativ einfach ermittelt werden.
Für die Durchführung der Berechnung von Übertragungssystemen oder der Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekannten Programmen wie MATLAB und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.
Alternativ können mit selbst erstellten beliebigen Rechenprogrammen bei Anwendung von Differenzengleichungen in Verbindung mit logischen Operatoren sehr effiziente Regelkreis-Simulationen durchgeführt werden. Dabei sind relativ geringe mathematische Kenntnisse erforderlich.
Treten Begrenzungseffekte im Regler oder Totzeitsysteme in der Regelstrecke auf, oder der Regler hat nichtlineare Eigenschaften wie der Zweipunktregler, kann das zeitliche Verhalten des Regelkreises nur numerisch mit der diskreten Zeit berechnet werden. Auch die Berechnung von dynamischen Systemen mit dem Verfahren der Zustandsraumdarstellung ist mit einem Totzeitsystem nicht ohne numerische Berechnung möglich.[12]
Die numerische Berechnung erlaubt tabellarisch und grafisch eine völlige Durchsicht des inneren Bewegungsablaufs dynamischer Übertragungssysteme. In Verbindung mit logischen Programmbefehlen und Wertetabellen lassen sich nichtlineare, begrenzende und totzeitbehaftete Systeme simulieren.
Methode der numerischen Berechnung[Bearbeiten | Quelltext bearbeiten]

Werden die Differenziale der Ausgangsgröße y(t) einer Differenzialgleichung durch kleine Differenzenquotienten mit als diskretisierte Zeit ersetzt, entsteht eine numerisch lösbare Differenzengleichung in Annäherung an die Differenzialgleichung. Zweckmäßig ist die Umwandlung linearer Elementarsysteme (Übertragungsfunktionen wie I-, PT1-, D-, PD1-Glieder) in Differenzengleichungen. Diese können je nach Lage der Funktionsblöcke im Signalflussplan mit nichtlinearen Systemen oder Systemen mit Totzeit und deren numerischen Berechnungsmethoden rekursiv behandelt werden.
Differenzengleichungen oder eine Kette von Differenzengleichungen, die mehrere hintereinander geschaltete Elementarsysteme beschreiben, lassen die Ausgangsgröße algebraisch für einen kleinen Zeitschritt in Abhängigkeit vom Eingangssignal errechnen. Die numerische Gesamtlösung des Systems erfolgt – bei einfachen Differenzengleichungen – rekursiv über viele Berechnungsfolgen in je kleinen konstanten Zeitintervallen. Die Form der Gesamtlösung ist damit tabellarisch. Alle Zeilen enthalten die gleichen Differenzengleichungen der Berechnungsfolge , alle Spalten berechnen die Folgen .
Differenzengleichungen lassen sich mit jeder Programmiersprache anwenden. Empfohlen wird die Verwendung der Tabellenkalkulation, weil die Anwendung einfach ist und Programmfehler damit ausgeschlossen sind.
Siehe ausführliche Details mit Anwendung Differenzengleichung (Differenzenverfahren)
Regelkreisentwurf[Bearbeiten | Quelltext bearbeiten]
Der Entwurf einer Regelung – die Verbindung eines geeigneten Reglers mit der Regelstrecke zu einem geschlossenen Kreis – ist die eigentliche Aufgabe der Regelungstechnik.
Häufige Anwendungen der Regelung physikalischer Größen[Bearbeiten | Quelltext bearbeiten]
Nachfolgende Auflistung nennt unabhängig von konkreten Anwendungen einige physikalische bzw. chemische Größen, die typischerweise als Regelgrößen auftreten.
- Temperaturregelung
- Druck- und Kraftregelung
- Durchfluss- und Mengenregelung
- Füllstandsregelung
- Lage-, Positions- und Entfernungsregelung
- Geschwindigkeits- und Beschleunigungsregelung
- Drehzahl- und Drehmomentregelung
- Regelung chemischer Größen, wie Konzentrationen, in der Verfahrenstechnik
Grundlagen des Regelkreises[Bearbeiten | Quelltext bearbeiten]
In einem einfachen Regelkreis zur Regelung beliebiger physikalischer Größen bestimmt die Größe des Sollwertes und das Zeitverhalten der Regelstrecke in Verbindung mit dem Zeitverhalten des angepassten Reglers den zeitlichen Verlauf der Regelgröße.
Die Aufgabe des Reglers besteht gewöhnlich darin, die Regelgröße der Führungsgröße möglichst gut anzunähern und den Einfluss von Störgrößen zu minimieren.
Ein stabiler Regelkreis kann bei Parameteränderungen des Reglers oder der Regelstrecke instabil werden, selbst wenn die einzelnen Bestandteile des Regelkreises für sich genommen stabil sind. Andererseits kann sich ein Regelkreis mit einem geeigneten Regler auch stabil verhalten, wenn einzelne Bestandteile der Strecke instabil sind. Eine positive Rückführung eines Regelkreises führt immer zur monotonen Instabilität.
Die P-Verstärkung eines Reglers kann in einem Regelkreis nicht beliebig hoch gewählt werden, anderenfalls führt infolge der phasenverschiebenden Eigenschaften aller zeitabhängigen Komponenten des Regelkreises – bedingt durch die negative Rückführung – zur oszillatorischen Instabilität. Wird z. B. ein variables Frequenzsignal konstanter Amplitude an den Eingang einer Regelstrecke mit mindestens drei PT1-Verzögerungsgliedern eingeleitet, dann fällt mit steigender Frequenz die Amplitude des Ausgangssignals und das Ausgangssignal ist gegenüber dem Eingangssignal nacheilend um verschoben. Wenn eine solche Regelstrecke in Verbindung mit einem Regler zu einem Regelkreis geschaltet wird, entsteht am Soll-Istwert-Vergleich für eine kritische Kreisverstärkung anstelle einer Gegenkopplung eine Mitkopplung und der Regelkreis wird oszillatorisch instabil.
Die Stabilität eines Regelkreises kann nach dem vereinfachten Nyquist-Kriterium durch die Darstellung des Amplitudengangs und des Phasengangs im Bode-Diagramm abgeschätzt werden:
- Ein geschlossener Regelkreis ist stabil, wenn der aufgeschnittene Regelkreis bei der Durchtrittsfrequenz für die Phasendrehung des Phasengangs ist. Diese Beziehung gilt für stabile Verzögerungsglieder (negative Realteile der Pole) bis zu einem Doppelpol im Ursprung und einem Totzeitglied der Regelstrecke.
Bei Angriff einer statischen oder flüchtigen Störgröße zeigt die Regelgröße zu diesem Zeitpunkt eine vorübergehende Regelgrößenänderung. Eine statische Störgröße kann eine bleibende Regelabweichung hervorrufen, wenn die Kreisverstärkung z. B. bei Verwendung eines stetigen proportionalen Reglers (P-Regler) nicht hoch genug ist. Hat der Regler eine zeitlich integrale Komponente (I-Glied), verschwinden statische Regelabweichungen, der Regelvorgang wird aber wegen der notwendigen Reduzierung der Kreisverstärkung langsamer.
Es ist Aufgabe des Reglers, das Zeitverhalten der Regelgröße bezüglich des statischen und dynamischen Verhaltens gemäß vorgegebenen Anforderungen festzulegen. Zur Erfüllung widersprechender Anforderungen wie gutes Führungs- und Störverhalten sind gegebenenfalls aufwändigere Regelkreisstrukturen erforderlich.
Die Übergangsfunktion (Sprungantwort der Regelgröße) eines Regelkreises mit einer Regelstrecke ab des zweiten Grades (ohne Pol-Nullstellen-Kompensation) verursacht je nach Höhe der Kreisverstärkung ein unvermeidbares periodisch gedämpftes Einschwingverhalten.
Die Führungsgröße des Regelkreises kann als fester Sollwert, als programmgesteuerte Sollwertvorgabe oder als kontinuierliches, zeitabhängiges Eingangssignal mit besonderen Folgeeigenschaften für die Regelgröße ausgelegt sein.
Kenngrößen der Übergangsfunktion des Regelkreises[Bearbeiten | Quelltext bearbeiten]
Ein Regelkreis mit linearen Komponenten der Regelstrecke höherer Ordnung, eventuell mit kleiner Totzeit und geringer Begrenzung der Stellgröße des Reglers hat die im Grafikbild dargestellte typische Übergangsfunktion (Sprungantwort). Die nachfolgenden tabellarisch aufgestellten Kenngrößen, die durch Führungsgrößensprünge oder Störgrößensprünge entstehen, hängen von den Regel- und Streckenparametern ab. Mit systematischer Änderung der Regelparameter lassen sich die gewünschten Eigenschaften der Kenngrößen (auch Güteforderungen, Dynamikforderungen) erreichen.
Die nachfolgenden Begriffe der Kenngrößen der Übergangsfunktion sind in der Fachliteratur meistens einheitlich geführt. Die zugehörigen Abkürzungen sind es nicht.[13]
Tabellarische Aufstellung der Kenngrößen der Übergangsfunktion eines Regelkreises:

| Bezeichnung | DIN IEC 60050 | DIN 19226 | Begriffsdefinition |
|---|---|---|---|
| Verzugszeit | Te | Tu | Zeit vom Eingangssprung nach Abschnitt der Wendetangente der Abszisse |
| Anstiegszeit (Ausgleichszeit) |
Tb | Tg | Tangente Abschnitt Abszisse nach Abschnitt Sollwert |
| Anregelzeit (Einschwingzeit) |
Tcr | Zeit vom Eingangssprung bis y(t) das Toleranzband schneidet. Kenngröße der Reaktionsgeschwindigkeit einer Regelung. | |
| Ausregelzeit (Ausschwingzeit) |
Tcs | Zeit vom Eingangssprung, bis die Schwingamplituden y(t) innerhalb des Toleranzbandes liegen. Kenngröße des Abklingens der Schwingamplituden. | |
| Überschwingweite | xm | Größte Amplitude über dem Beharrungswert der Regelgröße. Beharrungswert = Istwert für t → ∞. (Führungsgrößensprung = 1). | |
| Maximum der Regelgröße |
Überschwingweite + Beharrungswert |
Ließen sich diese Größen der Anregelzeit, der Ausregelzeit und der Überschwingweite gemeinsam minimieren, dann wäre der Regelkreis optimal dimensioniert. Leider zeigen die genannten Größen bei Änderung der Reglerparameter ein teilweise entgegengesetztes Verhalten. Erhöht man beispielsweise die Kreisverstärkung, verkürzt sich die Anregelzeit, die Ausregelzeit und die Überschwingweite vergrößern sich.
Der Regelkreis wird mit Hinblick auf das Führungs-, Stör- und Robustheitsverhalten optimiert. Welche Art der oben genannten Gütekriterien berücksichtigt werden soll, muss in einem Projekt-Lastenheft festgelegt werden.
Gütekriterien (Regelgüte, Integralkriterien, Güte des Regelverhaltens)
Man versteht darunter ein Maß für die zeitliche Abweichung der Sprungantwort der Regelabweichung y(t) zur Sprungfunktion der Führungsgröße w(t) über den vollen Einschwingvorgang durch Integration.
Bei diesen Integralkriterien wird die Regelabweichung w(t) – y(t) für die Dauer des Einschwingvorgangs auf verschiedene Arten integriert. Unterschieden wird die:
- lineare Regelfläche
- quadratische Regelfläche
- Betragsregelfläche: (Integration des Betrages der Regelabweichung)
- ITAE-Kriterium: Durch Multiplikation mit der Zeit werden die kleinen Schwingamplituden stärker berücksichtigt.
Komponenten des Regelkreises[Bearbeiten | Quelltext bearbeiten]

Je nach Anforderung der Qualität des Regelung, der Stückzahl der Regler, die Art der vorhandenen Signale der Strecke, die Art der gegebenen Hilfsstromversorgung und auch ob Sicherheitsvorschriften berücksichtigt werden müssen, kann entschieden werden, ob ein unstetiger Regler, ein analoger Regler, ein digitaler Regler und evtl. redundante Einrichtungen eingesetzt werden können.
Verhalten von stetigen Reglern:
- Regler mit P- oder PD-Verhalten lassen einen Regelkreis schnell reagieren.
- (Siehe Einfluss der Stellgrößenbegrenzung im übernächsten Abschnitt).
- Regler mit I-Anteil sind durch die (theoretisch) unendliche Verstärkung statisch genaue aber langsame Regler. Mit dem I-Anteil wird eine zusätzliche Polstelle in die Übertragungsfunktion des offenen Regelkreises eingefügt.
- Regler mit PI-Verhalten sind auch für Regelstrecken mit Totzeit geeignet.
- PID-Regler sind in der klassischen Form aus der Parallelschaltung der Einzelkomponenten entstanden. Durch algebraische Umrechnung der zugehörigen Übertragungsfunktion G(s) besteht der ideale PID-Regler aus zwei PD-Gliedern und einem I-Glied. Damit lässt sich die Parametrierung des Reglers für eine gegebene Regelstrecke höherer Ordnung für zwei dominante Zeitkonstanten unmittelbar festlegen. Für den offenen Regelkreis wird eine vollständige Kompensation der zwei Verzögerungsglieder der Regelstrecke vorgenommen. Gleichzeitig wird zusätzlich ein PI-Glied eingefügt. Die Größe des optimalen Verstärkungsfaktors kann empirisch oder in einer numerischen Simulation über die gewünschte Sprungantwort des geschlossenen Regelkreises bestimmt werden.
- Idealer PID-Regler in Parallelstruktur: .
- Idealer PID-Regler in Reihenstruktur: .
- Umrechnung PID-Regler der Reihenstruktur in Parallelstruktur: .
- Umrechnung PID-Regler der Parallelstruktur in Reihenstruktur: .
- Hinweis: Wenn der Inhalt des Wurzelzeichens negativ wird, entstehen konjugiert komplexe Nullstellen und damit entsteht ein PID-Regler 2. Ordnung mit einer Resonanzstelle. Dieser Regler könnte eine Regelstrecke 2. Ordnung mit konjugiert komplexen Polen vollständig kompensieren. Gleiche Zeitkonstanten vorausgesetzt.
- Ideale Regler gelten als technisch nicht realisierbar, wenn die Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist. Deshalb wird der Übertragungsfunktion des idealen Differenzierers eine kleine ungewollte, aber notwendige „parasitäre“ Verzögerung (PT1-Glied) zugefügt, deren Zeitkonstante wesentlich kleiner sein muss als die Zeitkonstante des Differenzierers .
- Spezialregler bedienen zahlreiche spezielle Anwendungen, wie Mehrgrößensysteme, Kaskadenregelung, Regelkreise mit Vorsteuerung und Vorfilter, Regelkreise mit Störgrößenaufschaltung, Folgeregelung nach einer Solltrajektorie, Mehrpunktregelung, Fuzzy-Regler, Zustandsregelung der Zustandsvariablen im Zustandsraum, Digitalregler. Gutes Führungsverhalten und gute Störunterdrückung erfordern Spezialregler, weil widersprechende Eigenschaften erforderlich.
Verhalten linearer Regelstrecken:
- Regelstrecken zweiten Grades (z. B. Reihenschaltung von zwei PT1-Gliedern oder PT1-Glied + I-Glied) können mit beliebig hoher Kreisverstärkung im Regelkreis ohne Gefahr der Instabilität arbeiten.
- Regelstrecken dritten und höheren Grades können im stabilen Regelkreis nur mit stark eingeschränkter Kreisverstärkung wirken.
- Bei drei Verzögerungsgliedern mit dem ungünstigsten Fall von drei gleichen Zeitkonstanten ist der Grenzfall der Instabilität bei einer P-Verstärkung des Reglers von K = 8 gegeben, unabhängig von der Größe der Zeitkonstanten. Erklären lässt sich dieses Verhalten mit dem Stabilitätskriterium von Nyquist.
- Eine Regelstrecke beliebig höheren Grades, evtl. zusätzlich mit Totzeitverhalten, kann nur stabil geregelt werden, wenn einige der PT1-Glieder durch PD1-Glieder des Reglers kompensiert werden.
- Beispiel Regelstrecke 4. Grades mit Totzeitglied:
- Ein monoton instabiles Regelstreckenglied kann mit einem geeigneten Regler zu einem stabilen Regelkreis führen.
- Beispiel eines monoton instabilen Regelstreckengliedes:
- Eine aus reiner Totzeit bestehende Regelstrecke kann nur – abgesehen von Spezialreglern – durch einen I-Regler geregelt werden.
- Wählt man für die Verstärkung des I-Reglers , beträgt für alle Totzeiten die Überschwingung ca. ü = 4 %, was einer Dämpfung von ca. D = 0,7 entspricht.

Einfluss der Stellgrößenbegrenzung:
Es ist Ermessenssache, ob das Reglerausgangssignal mit der Leistungsschnittstelle als Stellgröße, Teil des Reglers, der Regelstrecke oder eine unabhängige Einrichtung ist.
- Sind differenzierende PD-Glieder im Regler vorhanden, wird die Verstärkung um einen dynamischen Anteil noch zusätzlich erhöht. Dabei kann die Stellgröße sehr große Werte annehmen. Dies ergibt sich aus der Berechnung der Schließbedingung (Signalflussalgebra) des Regelkreises.
- Eine hohe Kreisverstärkung (P-Verstärkung des Reglers und der Strecke) macht den Regelkreis dynamisch schnell, sie kann aber praktisch nur begrenzt realisiert werden, weil die Stellgröße des Reglers wegen technischer Anschläge oder aus Energiemangel nicht unbegrenzt wachsen kann.
- Stellgrößenbegrenzungen bei Anwendung von P-Reglern sind häufig gegeben, sie verlangsamen das Einschwingverhalten der Regelgröße. Die Störgrößeneinflüsse werden weniger reduziert.
- Begrenzungen der Stellgröße des Reglers führen zur Nichtlinearität des Systems. Eine Beschreibung des Systems mit der Übertragungsfunktion ist damit nicht gültig.
- Man kann durchaus Signalbegrenzungen ignorieren und kommt zu einem stabilen Regelkreis. Jedoch entspricht das Übergangsverhalten der Regelgröße y(t) bei Signalbegrenzungen nicht der Übertragungsfunktion des Regelkreises.
- Eine geringere Regler-Verstärkung in Verbindung mit einer zeitlich integral wirkenden Komponente des Reglers macht den Regelkreis für alle statischen Einflüsse zwar genauer und stabiler, aber deshalb auch langsamer.
- Eine zu einer Regelstrecke umfunktionierte Steuerstrecke lässt sich ohne Energiezufuhr nicht schneller machen.
Regelkreis-Entwurfsstrategien für lineare zeitinvariante Systeme[Bearbeiten | Quelltext bearbeiten]
Die Stabilität des Regelkreises mit linearen zeitinvarianten Übertragungssystemen hängt von der Ordnung und den Parametern der Strecke, von der Struktur des Reglers und von den Parametern – insbesondere von der P-Verstärkung – des Reglers ab.
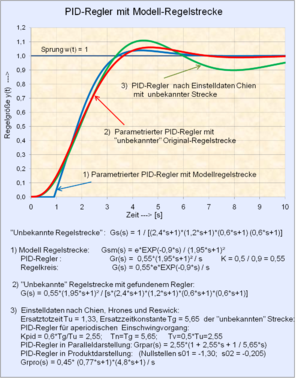
1) Parametrierter PID-Regler an Modellregelstrecke.
2) Gleicher PID-Regler an Original-Regelstrecke.
3) Mittels heuristischer Methoden parametrierter PID-Regler an Original-Regelstrecke
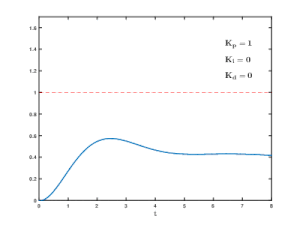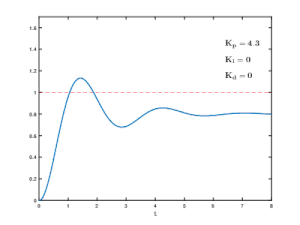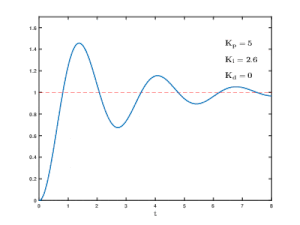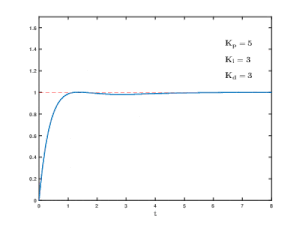
Die Entwurfsstrategien für Regelkreise beziehen sich bei linearen Systemen auf die Minimierung der statischen Regelabweichung und des Einschwingverhaltens der Regelgröße. Je geringer beispielsweise die Zahl und die Größe der Zeitverzögerungen der Regelstrecke sind, umso höher kann die Kreisverstärkung und damit die Verstärkung des Reglers gewählt werden, was die statische und dynamische Genauigkeit der Regelgröße verbessert.
Liegt die Beschreibung der Regelstrecke als lineares zeitinvariantes Übertragungssystem in Produktdarstellung vor, kann relativ einfach ein geeigneter Regler bestimmt werden. Zur Vereinfachung des offenen Regelkreises werden PT1-Glieder mit dominantem Zeitkonstanten der Strecke gegen PD1-Glieder des Reglers gekürzt (Pol-Nullstellenkompensation), d. h., die Regelkreisglieder des offenen Kreises mit gleichen Zahlenwerten und mit gleichen Vorzeichen der Pole und Nullstellen haben damit keine Wirkung mehr. Für die Stabilität des Regelkreises ist jeweils 1 Pol mehr erforderlich als Nullstellen innerhalb der Übertragungsfunktion vorhanden sind.
Mit Hilfe der Gleichung für das Schließen des Regelkreises ergibt sich die Übertragungsfunktion des geschlossenen Regelkreises in Polynomdarstellung. Die Schließbedingung gilt nicht für Regelstrecken mit Totzeit.
Die Übergangsfunktion (Sprungantwort der Regelgröße) eines Regelkreises mit einem P-Regler und einer Regelstrecke mit Verzögerungen ab zweiten Grades verursacht je nach Höhe der Kreisverstärkung ein unvermeidbares periodisch gedämpftes Einschwingverhalten. Normalform der Übertragungsfunktion eines Schwingungsgliedes: .
Dieses periodisch gedämpfte Einschwingverhalten ändert sich auch nicht bei Regelstrecken höheren Grades oder mit Totzeit bei reduzierter Kreisverstärkung, lediglich die Verzugszeit und Ausregelzeit werden größer. Selbstverständlich erfordern Regelkreise mit geringer Kreisverstärkung einen I-Anteil zur Vermeidung einer großen Regelabweichung.
Zur Beurteilung des Einschwingverhaltens wurde dazu der Begriff Regelgüte definiert, die je nach Vorgabe eines Lastenheftes die Art des Einschwingens der Regelgröße festlegt.

Bei Regelstrecken mit nichtregulären Systemen wie das monoton instabile PT1i-Glied oder bei instabilen Regelstrecken mit zwei I-Gliedern wird der geschlossene Regelkreis mit einem geeigneten Regler mit steigender Kreisverstärkung stabil. Bei solchen Systemen empfiehlt es sich, die Stabilität des Regelkreises mittels numerischer Berechnung zu prüfen.
Weitere Entwurfskriterien:
- Wird eine Steuerstrecke aus linearen zeitinvarianten Systemen in Verbindung mit einem Regler zu einem Regelkreis gestaltet, dann werden in Bezug zum Verhalten der Steuerstrecke 2 Vorteile gewonnen:
- Die Regelgröße stellt sich auf das Niveau des Sollwertes ein, Störgrößen werden minimiert,
- Die dominante Zeitkonstante der Regelgröße verringert sich gegenüber die der Strecke ungefähr um den Faktor der Kreisverstärkung.
- Der Regelkreis soll sich robust verhalten.
- Unter „robust“ versteht man den Einfluss der schleichenden Änderungen der Parameter von Regler und Regelstrecke auf die Dynamik des Regelkreises. Diese durch innere und äußere Umwelteinflüsse wie z. B. Alterung, Reibung, Korrosion entstehenden Parameteränderungen müssen innerhalb eines zugelassenen Toleranzbereiches liegen. Das Verhalten der Robustheit wird auch mit Einfluss der „inneren Störgrößen“ eines Regelkreises bezeichnet.
- Kompromiss zur Reglerparametrierung:
- In Einzelfällen muss immer für eine gute Dynamik des Regelkreises ein Kompromiss zwischen einer zulässigen Stellgrößenbegrenzung oder einer Reduzierung der P-Verstärkung und Einfügen eines I-Anteils im Regler entschieden werden. Gleichzeitiges Verbessern des Einschwingverhaltens der Regelgröße und der Störunterdrückung erfordern weitere Maßnahmen wie Vorfilter oder Vorsteuerung.
- Simulation des Regelkreises zur Reglerparametrierung:
- Zur Simulation des Verhaltens eines Regelkreises muss das mathematische Modell der Regelstrecke ermittelt werden. Dazu eignen sich experimentelle Identifizierungsmaßnahmen (Experimentelle Systemidentifikation) mit Hilfe von Testsignalen.
- Für die Berechnung des zeitlichen Verhaltens von Übertragungssystemen mit Signalbegrenzungen und Totzeitverhalten eignet sich nur die Methode der numerischen Berechnung mit der diskreten Zeit .
Übersicht Regelung mit nichtlinearen Reglern[Bearbeiten | Quelltext bearbeiten]

Bei linearen Systemen ohne Energiespeicher ist die Ausgangsgröße proportional der Eingangsgröße. Bei linearen zeitinvarianten (LZI-System) Systemen mit Energiespeichern ist die Ausgangsgröße im eingeschwungenen Zustand der Eingangsgröße proportional. Bei Systemen mit integralem Verhalten (I-Glied) ist die Ausgangsgröße proportional des zeitlichen Integrals der Eingangsgröße. Bei Systemen mit differenzierendem Verhalten (D-Glied) ist die Ausgangsgröße proportional des Differentialquotienten der Eingangsgröße.
Mathematische Operationen von Signalen bezogen auf die Ausgangsgröße wie:
- Additionen, Subtraktionen, Differentiationen, Integrationen oder Multiplikationen mit einem konstanten Faktor von Eingangssignalen ergeben lineares Verhalten.
- Multiplikation und Division von Eingangsgrößen ergeben nichtlineares Verhalten.
Bei nichtlinearen Übertragungssystemen wirkt mindestens eine nichtlineare Funktion in Verbindung mit linearen Systemen. Nichtlinearen Funktionen werden nach stetigen und unstetigen Nichtlinearitäten unterschieden. Stetige Nichtlinearitäten weisen keine Sprünge der Übertragungskennlinie auf wie z. B. bei quadratischem Verhalten. Unstetige Übertragungskennlinien wie bei Begrenzungen, Hysterese, Ansprechempfindlichkeit, Zwei- und Mehrpunkt-Charakter haben keinen kontinuierlichen Verlauf.
Zu den nichtlinearen Reglern gehören auch die unstetigen Regler wie Zweipunkt-, Mehrpunkt- und Fuzzy-Regler, die in einem eigenen Kapitel beschrieben sind.
Die Berechnung von nichtlinearen Systemen geschieht meist im Zeitbereich. Die Lösung von nichtlinearen Differentialgleichungen ist schwierig und aufwendig. Dies bezieht sich besonders auf die Gruppe der Systeme mit unstetigem nichtlinearem Übertragungsverhalten bzw. nichtstetigen Reglern. Einfacher ist die Berechnung eines Regelkreises mit schaltenden Reglern mit rechnergestützten zeitdiskreten Verfahren.
- → Siehe Kapitel Regelkreis#Reglerentwurf für lineare zeitinvariante Systeme
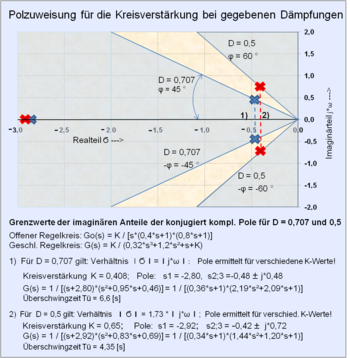
Entwurf eines Reglers durch Polzuweisung in der s-Ebene[Bearbeiten | Quelltext bearbeiten]
Das nachfolgend beschriebene Entwurfsverfahren besteht darin, dass Pole und Nullstellen einer Übertragungsfunktion eines geschlossenen Regelkreises in bestimmte Bereiche des Pol-Nullstellen-Diagramms (siehe auch Polvorgabe im Zustandsraum) zugewiesen werden, um bestimmte Güteanforderungen festzulegen. Dabei wird vorausgesetzt, dass ein dominantes Schwingungsglied (PT2-Glied) vorliegt, evtl. vorhandene zusätzliche Pole weit genug vom dominanten Polpaar entfernt in der linken s-Halbebene liegen und deshalb wenig Einfluss haben.
Aufgabe eines Reglers ist nun, die zugewiesene Lage der Pole zu erfüllen.
Reglerentwurf mit der inversen Laplace-Transformation[Bearbeiten | Quelltext bearbeiten]
Ist die Übertragungsfunktion eines linearen dynamischen Systems oder eines geschlossenen Regelkreises gegeben, kann mittels der inversen Laplace-Transformation mit einem definierten Eingangs-Testsignal der Verlauf der Ausgangsgröße bzw. die Regelgröße errechnet und graphisch dargestellt werden. Dabei bedient man sich einer in jedem Fachbuch der Regelungstechnik vorhandenen Laplace-Transformationstafel, welche für viele Formen der Produktdarstellung einer Übertragungsfunktion im s-Bereich die korrespondierende Funktion im Zeitbereich darstellt.
Die Ausgangsgröße eines dynamischen Systems im s-Bereich lautet:
Die Ausgangsgröße eines dynamischen Systems y(t) des Zeitbereichs für ein Übertragungssystem im s-Bereich lautet:
Testsignale zur Berechnung der Systemantwort:
Testsignal Zeitbereich f(t) Testsignal im s-Bereich Systemantwort f(t) Impulsfunktion Normierter Impuls = Gewichtsfunktion Sprungfunktion Einheitssprung für Übergangsfunktion Anstiegsfunktion
Gradient:Rampenantwort
Die grafische Darstellung der Sprungantwort (Übergangsfunktion) eines dynamischen Systems ist die häufigste bekannte Darstellung des System-Zeitverhaltens. Wird als Suchbegriff die korrespondierende Zeitfunktion in den Laplace-Korrespondenztabellen gefunden, kann durch Einsetzen verschiedener Werte für t das Systemverhalten für ein gegebenes Eingangssignal grafisch dargestellt werden.
Anmerkung: Die Anwendung der inversen Laplace-Transformation fordert bei gedämpft schwingenden Systemen viel Rechenarbeit mit trigonometrischen und exponentiellen Funktionen.
→ Siehe Berechnungsbeispiel auch Regelkreis#Reglerentwurf mit der inversen Laplace-Transformation
Digitale Regelung (Übersichtsdarstellung)[Bearbeiten | Quelltext bearbeiten]
Analoge wie digitale Regler benötigen als Eingangssignal die Regelabweichung und einen Regelalgorithmus, der die gewünschte Dynamik des geschlossenen Regelkreises bestimmt.
Zeitdiskrete lineare dynamische Systeme sind dadurch gekennzeichnet, dass die inneren Systemzustände nur zu einzelnen Zeitpunkten definiert sind und an den Ein- und Ausgängen zeitdiskrete Signale auftreten.
Bei den meisten Regeleinrichtungen handelt es sich bei den Regelstrecken um kontinuierlich wirkende analoge Eingrößensysteme, die sich linear, nichtlinear und totzeitbehaftet verhalten können. Für diese Regelstrecken sollen bestimmte physikalische Größen wie Temperatur, Kraft, Druck, Geschwindigkeit, Niveau usw. geregelt werden. Die dafür erforderlichen Regler können eine analoge oder digitale Systemstruktur aufweisen und enthalten am Ausgang eine analoge kontinuierlich wirkende Stellgröße.
Digitale Regelung bedeutet, dass das Eingangssignal eines Reglers oder eines Teilsystems zu bestimmten diskreten Zeitpunkten abgetastet, zeitsynchron berechnet und als digitales Ausgangssignal ausgegeben wird. Andere Begriffe bezeichnen diesen Vorgang als „zeitdiskrete Regelung“ oder auch als „Abtastregelung“.
In der Mathematik wird eine Auflistung von endlich und unendlich vielen fortlaufend nummerierten Objekten (hier abgetastete Zahlenwerte) als Folge bezeichnet. Die Abtastfolge bedeutet eine Nummerierung der Folgeglieder der Wertefolge des Eingangssignals (Eingangsfolge) und des Ausgangssignals (Ausgangsfolge) eines Systems.
Eine Wertefolge besteht aus oder vielen Folgegliedern.
Der digitale Regler hat keine Begrenzung der Anzahl der Folgeglieder der Abtastfolge. Es werden bei einer Regelung unendlich viele Folgeglieder im realen zeitlichen Abstand der Abtastzeit ausgeführt.
Der Rechenalgorithmus eines Digitalrechners erlaubt keine kontinuierliche Berechnung von analogen zeitabhängigen Signalen. Deshalb werden zu bestimmten Zeitpunkten die analogen Eingangssignale, z. B. die Regelabweichung , mit Hilfe eines (idealen) -Abtasters und einem A/D-Wandlers als abgetastet. Das gewünschte System-Übertragungsverhalten des digitalen Reglers wird für die gegebene Eingangsfolge mit Differenzengleichungen berechnet und taktsynchron als digitales Ausgangssignal mit Zahlenwerten ausgegeben.
Ist ein analoges Ausgangssignal als Stellgröße für eine analoge stetig wirkende Regelstrecke erforderlich, erlaubt eine spezielle Hardware mit einem D/A-Wandler mit einer Haltefunktion (Halteglied) die Umwandlung in ein gestuftes quasi-stetiges Ausgangssignal als Stellgröße des Reglers.
Bei schnellen Regelstrecken spielen die Systemgeschwindigkeiten des digitalen Rechners, der A/D-D/A-Wandler, die Sample-and-Hold-Schaltung, wie auch die verwendeten Methoden der Differenzengleichungen beziehungsweise deren Approximations-Algorithmen eine große Rolle.
Zu den technischen Vorteilen der digitalen Regler gehören: einmaliger Hardware-Entwicklungsaufwand, einfache parametrische System-Änderungen per Software, Realisierung komplexere Reglerstrukturen, Multitasking.

Grundlagen Zustandsregelung[Bearbeiten | Quelltext bearbeiten]
Der Zustandsregler ist kein eigenständiger Regler, sondern er entspricht der mit Faktoren bewerteten Rückführung der Zustandsgrößen eines mathematischen Modells der Regelstrecke im Zustandsraum.
Das Grundprinzip des Zustandsreglers (auch statische Zustandsrückführung genannt) ist die Rückführung der bewerteten inneren Systemgrößen eines Übertragungssystems zu einem Regelkreis. Die einzelnen Zustandsgrößen werden mit Faktoren bewertet und wirken subtraktiv auf die Führungsgröße .
Damit durchlaufen Anteile der Zustandsgrößen ein zweites Mal die Integrationskette der Rechenschaltung laut Signalflussplan der Regelungsnormalform. Das Ergebnis ist ein Zustandsregler mit PD-Verhalten im Zustandsregelkreis.
Im Gegensatz zu einem Standardregelkreis wird die Ausgangsgröße des Zustandsregelkreises nicht auf den Eingang der Regelstrecke zurückgeführt. Der Grund liegt darin, dass die Ausgangsgröße eine Funktion der Zustandsgrößen ist. Dennoch kann ein nicht akzeptabler proportionaler Fehler zwischen den Werten der Führungsgröße und der Regelgröße entstehen, der durch ein Vorfilter V beseitigt werden muss.
Die Regler-Zustandsrückführung (zur Unterscheidung der Rückführung der Zustandsgrößen) bezieht sich auf den Zustandsvektor , der mittels Vektorverstärkung laut dem Signalflussplan des Modells der Zustandsregelkreises auf die Eingangsgröße zurückgeführt wird:
Der lineare Zustandsregler bewertet die einzelnen Zustandsvariablen der Regelstrecke mit Faktoren und summiert die so entstandenen Zustandsprodukte zu einem Soll-Ist-Wert-Vergleich.[14]
Eine Alternative zur Vermeidung einer Regelabweichung bietet ein überlagerter Regelkreis des Zustandsregelkreises mit einem PI-Regler mit Rückführung der Regelgröße y(t), der das Vorfilter V überflüssig macht.
Fuzzy-Regler[Bearbeiten | Quelltext bearbeiten]

Fuzzy-Regler beziehen sich auf die Verfahren der Fuzzy Controller, sind aber meist funktionelle Abwandlungen, Vereinfachungen oder Ergänzungen mit der Fuzzy-Logik.
Im systemanalytischen Sinne ist ein Fuzzy Control System ein statisches nichtlineares Steuersystem, welches aus scharfen Eingangsgrößen eines komplexen Prozesses nach den Regeln einer Regelbasis unscharf definierte fuzzifizierte Steuergrößen und scharfe defuzzifizierte Wertesignale bildet, mit denen ein zufriedenstellendes Prozessergebnis erreicht wird.
Fuzzy-Controller arbeiten mit sogenannten „linguistischen Variablen“, welche sich auf „unscharfe Mengenangaben“ beziehen, wie zum Beispiel hoch, mittel und niedrig. Die „Regelbasis“ verknüpft die fuzzifizierten Ein- und Ausgangssignale mit logischen Regeln wie WENN-Teil und DANN-Teil. Mit der Defuzzifizierung wird die unscharfe Menge wieder in scharfe Stellbefehle gewandelt (z. B. Ventilkombinationen für „Kraft Aufbau“ oder „Kraft Abbau“ oder „Kraft halten“).
Ein grafisches Fuzzy-Modell zeigt eine Fuzzy-Variable als skalierte Grundmenge (z. B. Temperaturbereich), deren meist dreieckförmige Teilmengen (Fuzzy-Sets) auf der Abszisse eines Koordinatensystems meist überlappend aufgeteilt sind. Die Ordinate zeigt den Zugehörigkeitsgrad für jeden scharfen Wert der Eingangsgröße an. Der maximale Wert des Zugehörigkeitsgrades für jeden Fuzzy-Set beträgt μ = 1 ≡ 100 %.
Unstetige Regler[Bearbeiten | Quelltext bearbeiten]

Bei unstetigen Reglern (auch nichtstetige Regler) ist die Ausgangsgröße u(t) gestuft. Bei einem einfachen Zweipunktregler kann die Ausgangsgröße des Reglers – die Stellgröße u(t) – nur 2 diskrete Zustände annehmen: Ist die Regelabweichung e(t) = w(t) – y(t) positiv, schaltet der Zweipunktregler ein, ist sie Null oder negativ schaltet der Regler aus. Hat der Regler eine symmetrische Hysterese, muss die Regelabweichung stets einen kleinen Betrag negativ werden, damit der Regler ausschaltet und einen gleichen kleinen Betrag positiv werden, damit der Regler einschaltet.
Unstetige Regler mit den Ausgangssignalzuständen „Ein“ oder „Aus“ können auch ein proportionales Verhalten haben, wenn die Ausgangsgröße eines klassischen Standardreglers mit einem Pulsdauer-Modulator versehen wird. Die Regelstrecke wirkt dabei zur Glättung der gepulsten Signale als Tiefpass. Zweck dieses Verfahrens ist die möglichst verlustfreie Steuerung großer Energieflüsse.
Bei der Verwendung elektrischer und elektronischer Schaltelemente wie Relais, Schaltschütze, Transistoren und Thyristoren ist eine möglichst niedrige Schaltfrequenz anzustreben, um Bauelemente-Verschleiß und Alterung gering zu halten. Auch elektronische Bauelemente unterliegen einer Alterung, wenn sie bei erhöhter innerer Temperatur betrieben werden. Andererseits bedeutet eine niedrige Schaltfrequenz eine Erhöhung der Welligkeit des Signals der Regelgröße.
Wegen der durch steile Impulsflanken verursachten elektromagnetischen Störungen der Schaltvorgänge sind geeignete Entstörmaßnahmen vorzusehen. (Siehe Elektromagnetische Verträglichkeit)
Wie auch bei linearen Übertragungssystemen interessiert die Stabilität eines Regelkreises mit nichtstetigen Reglern.
Die effektivste Berechnungsmethode für den Entwurf, die Analyse und der Optimierung eines nichtstetigen Reglers im Regelkreis-Modell ist numerisch durch kommerzielle Rechenprogramme wie mit MATLAB oder Simulink zu erreichen.
Liegen solche Rechenprogramme nicht vor, so können mit der Kombination logischer Gleichungen und Differenzengleichungen beliebige Systeme und Regelkreise mit stetigen, unstetigen, nichtlinearen und linearen Elementen relativ einfach mit beliebigen Rechenprogrammen – vorzugsweise Tabellenkalkulation – numerisch für eine diskrete Zeit Δt berechnet werden. Das Verhalten der relevanten Regelkreissignale für ein Test-Eingangssignal kann direkt tabellarisch und grafisch dargestellt werden.
siehe Hauptabschnitt "Unstetige Regler" Regler#Unstetige Regler
Stabilität[Bearbeiten | Quelltext bearbeiten]
Es existieren verschiedene Definitionen und Begriffe der Stabilität. Ein Übertragungssystem kann monoton oder oszillatorisch instabil sein. Ein falsch dimensionierter Regler kann in einem Regelkreis zur oszillatorischen Instabilität führen.
Stabilitätsverfahren siehe Abschnitt Regelkreis#Stabilität des Regelkreises
Mathematische Modelle der Regelstrecken[Bearbeiten | Quelltext bearbeiten]
Modelle beschreiben im Allgemeinen das zeitliche Verhalten dynamischer Systeme. Neben physikalischen materiellen Modellen (Beispiel: experimentelle Informationsgewinnung des Strömungsverhaltens eines Fahrzeugs im Windkanal, Modellschiffe im hydraulischen Kanal), die aufwendig und kostspielig sind, eignen sich besonders mathematische Systembeschreibungen für die Anwendung der Prozess-Simulation am Digitalrechner.
Die Vorteile der Prozess-Simulation sind bekannt, in weiten Grenzen sind Parameteränderungen möglich, zerstörungsfreie Untersuchungen möglich, relativ geringe Personalkosten,
Zur Modellgewinnung unterscheiden sich die Verfahren der theoretischen, analytischen und experimentellen Modelle.
Je nach Vollständigkeit der Kenntnisse der Modelle werden auch folgende Modellbegriffe verwendet:
- Black-Box-Modelle sind unbekannte Systeme, deren Art der Eingangs- und Ausgangsgrößen bekannt sind.
- Grey-Box-Modelle beschreiben meist Systeme deren Strukturen bekannt sind.
- Einfaches Beispiel: Regelstrecke mit Totzeit, globales I-Verhalten und Anschlagbegrenzung der Stellgröße.
- White-Box-Modelle beschreiben meist Systeme, deren mathematisches Verhalten bekannt ist, deren Parameter noch bestimmt werden müssen.
Für die Analyse, Synthese und Regelung von realen Übertragungssystemen (Regelstrecken), die meist als ein Hardwaresystem vorliegen, ist ein mathematisches Modell des Systems erforderlich.
Modelle in Form von Differenzialgleichungen beschreiben das zeitliche Verhalten des Systems. Sind diese Differenzialgleichungen oder zugehörigen Übertragungsfunktionen nicht gegeben, kann das zeitliche Verhalten eines Hardwaresystems durch experimentelle Identifizierungsmaßnahmen (Experimentelle Systemidentifikation) mit Hilfe von Testsignalen ermittelt werden.
Bei der prinzipiellen Vorgehensweise wird der Identifikationsalgorithmus für die Modellparameter solange verändert, bis für ein gegebenes Eingangssignal u(t) die Differenz der Ausgangsgrößen y(t) – yModell(t) innerhalb eines beliebigen Zeitablaufs des gemessenen Originalausgangs mit dem Modellausgang annäherungsweise verschwindet.
Dynamische Systeme mit konzentrierten Parametern als Eingrößen- und Mehrgrößensysteme können sich linear, nichtlinear, zeitinvariant, zeitvariant und global-proportional, -integral und -differenzial verhalten. Systeme mit konzentrierten Parametern (Feder-Masse-System) haben im Gegensatz zu Systemen mit verteilten Parametern (Wärmefluss im homogenen Medium) keine räumliche Ausdehnung.
Die Aufgabe eines mathematischen Modells eines realen dynamischen Prozesses oder eines noch zu projektierenden technischen Prozesses dient dem Erkennen und der Vorhersage des Systemverhaltens.
Das mathematische Modell eines Regelkreises beschreibt alle äußeren Einflussgrößen wie Störgrößen und Eingangssignale auf den geschlossenen Wirkungsablauf des Regelkreises. Das Verhalten der Ausgangsgrößen wie die Regelgrößen sowie auch interessante Zwischengrößen (Stellgrößen) als Funktion der Eingangssignale und der Parameter von Regler und Regelstrecke sind von besonderem Interesse.
Je nach Lastenheft der regelungstechnischen Aufgabenstellung ist für die Bestimmung eines geeigneten Reglers das mathematische Modell der Regelstrecke erforderlich.
In den meisten Anwendungsfällen haben Übertragungssysteme (Regelstrecken) auch nichtlineare Komponenten und sind totzeitbehaftet. Für solche Systeme wird experimentell durch geeignete Testsignale die Systemantwort aufgezeichnet und ein mathematisches Modell gesucht, das den gemessenen Verlauf der Ausgangsgröße reproduziert (= Experimentelle Prozessanalyse). Ein derartig definiertes Modell ist durch Anwendung numerischer Verfahren einfach berechenbar. Sind nichtlineare Teilsysteme im Gesamtsystem enthalten, müssen diese getrennt erfasst und durch Wertetabellen definiert werden.
- Global-proportionale zeitinvariante Regelstrecken höherer Ordnung mit Totzeit lassen sich relativ genau durch zwei PT1-Glieder und einem Tt-Glied beschreiben.
Falls die Darstellung der transzendenten Funktion des Totzeitgliedes mit dem Rechenprogramm Probleme bereitet, kann die dargestellte Modellgleichung auch praktisch identisch durch eine sehr gute Annäherung mit Ersatztotzeiten durch z. B. n = 3 PT1-Glieder wie folgt dargestellt werden:
- Global-integrale zeitinvariante Regelstrecken lassen sich ebenso durch zwei PT1-Glieder, einem I-Glied und einem Tt-Glied beschreiben.
Zum Modellverständnis eines dynamischen Systems müssen die wichtigsten Begriffe der inneren Systemspeicher verstanden werden.
Experimentelle Identifikation einer Regelstrecke mit Hilfe einer Modellregelstrecke[Bearbeiten | Quelltext bearbeiten]
Eine reale Regelstrecke lässt sich durch die Sprungantwort der Regelstrecke, durch die Impulsantwort der Regelstrecke oder auch durch Einspeisung einer variablen Frequenz identifizieren.

Wichtigste Merkmale für die Anwendung einer Modellregelstrecke mit Hilfe der Sprung- oder Impulsantwort sind:
- Die Parameter einer Regelstrecke können mittels einer einfachen Modellregelstrecke ermittelt werden, indem die Kennlinie des Modells durch schrittweises Ändern der Zeitkonstanten des Modells auf die Kennlinie der unbekannten Regelstrecke angepasst wird.
- Das Modell muss ähnliche Streckeneigenschaften aufweisen, wie die unbekannte Regelstrecke.
- Bei Strecken ohne Ausgleich benötigt das Modell einen I-Anteil, bei Strecken mit Totzeit ist für das Modell ebenfalls ein Totzeitglied erforderlich.
- Die Anpassung eines Modells an die unbekannte Regelstrecke mit Hilfe der Sprungantwort ist relativ einfach und kann evtl. auch grafisch durchgeführt werden.
- Das Anpassung eines Modells an die unbekannte Regelstrecke mit Hilfe der Impulsantwort ist etwas aufwendiger, bietet aber bei Deckungsgleichheit der Kennlinien eine völlige Übereinstimmung zwischen Original und Modell in einem Regelkreis im Vergleich mit den jeweiligen Sprungantworten. Mit diesem Modell lässt sich auch die Ordnung des Originals feststellen.
- Es sollte einfach zu realisieren sein.
Siehe Hauptartikel Regelstrecke#Experimentelle Identifikation einer Regelstrecke mit Hilfe einer Modellregelstrecke
Heuristische Einstellregeln für einfache Regelungen[Bearbeiten | Quelltext bearbeiten]

Die von Ziegler-Nichols bereits in den 1940er Jahren experimentell durchgeführten Einstellregeln beziehen sich auf die Sprungantwort einer Regelstrecke und definieren sie durch Anlegen einer Tangente am Wendepunkt als Strecke mit einem PT1-Glied und einem Totzeitglied. 1952 wurden von Chien, Hrones und Reswick die Einstellregeln (Faustformelverfahren (Automatisierungstechnik)) erweitert für aperiodisches Verhalten der Sprungantworten der Regelgröße und für gedämpft schwingendes Verhalten mit 20 % Überschwingungen. Zusätzlich erfolgt für beide Gruppen noch die Aufteilung in Führungsverhalten und Störverhalten. Diese Einstellregeln werden gelegentlich auch mit Faustformeln bezeichnet.
Es wird eine Regelstrecke 4. Ordnung mit folgender Übertragungsfunktion betrachtet:
Mit dem Anlegen der Tangente an die Übergangsfunktion der angegebenen Übertragungsfunktion ergeben sich die Kennwerte:
- Ersatztotzeit:
- Ersatzzeitkonstante:
Für diese Kennwerte werden anhand von Tabellen die Parameter der linearen Standardregler bestimmt. Aus diesen Kennwerten lässt sich keine Ersatzübertragungsfunktion bestimmen. Die Qualität der auf diese Weise ermittelten Reglerparameter ist ungünstig.
Eine Ersatzübertragungsfunktion eines sehr genauen Modells der oben genannten Übertragungsfunktion mit Hilfe einer Simulation mittels numerischer Berechnung lautet:
Siehe auch Regelstrecke#Experimentelle Identifikation einer Regelstrecke mit Hilfe einer Modellregelstrecke.
Lastenheft für ein Regelsystem[Bearbeiten | Quelltext bearbeiten]
Für eine anspruchsvolle Regelung – jenseits des Probierverfahrens – ist für die Bestimmung des Reglers neben der Kenntnis des mathematischen Modells der Regelstrecke ein Lastenheft für das Verhalten des Regelkreises erforderlich.
Folgende Kenntnisse der Eigenschaften der Regelstrecke bzw. eines Modells sind erforderlich:
- Liegen Signalbegrenzungen im Übertragungssystem vor, z. B. wenn man die erforderliche gerätetechnische Stellgrößeneinrichtung des Reglers in die Regelstrecke einbezieht
- Ist eine Totzeit im System vorhanden
- Hat die Regelstrecke grenzwertstabile Komponenten (I-Glieder)
- Enthält das Übertragungssystem gedämpft schwingende Komponenten, d. h. konjugiert komplexe Pole?
- Sind neben den LZI-Systemen nichtlineare Anteile (nichtlineare Kennlinie) im Übertragungssystem enthalten
- Enthält das Übertragungssystem instabile Komponenten, d. h. die Regelstrecke ist instabil?
- Hat die Regelstrecke mehrere Eingangs- und Ausgangsgrößen, d. h. Einschleifensystem (SISO)- oder Mehrgrößensystem (MIMO).
Folgende Beschreibung der Signale und des Verhaltens der Regelgröße im Regelkreis sind notwendig:
- Groß- und Kleinsignalverhalten des Einschwingens der Regelgröße auf den Sollwert.
- Hinweis: Das Großsignalverhalten wird durch Signalbegrenzungen innerhalb des offenen Regelkreises gestört!
- Art des Einschwingverhaltens der Regelgröße,
- Gütekriterien: asymptotisch, überschwingend, Dämpfung, Überschwingweite, Anregel- und Ausregelzeit, stationäre Regelabweichung, Langzeittoleranz
- Einfluss, Art und Angriffspunkt der Störgröße z. B. auf den Eingang oder Ausgang der Regelstrecke
- Folgeverhalten der Regelgröße nach einer definierten Führungsgröße
- Optimierung des Führungs- oder des Störverhaltens
- Genügt ein angenähertes Modell der Regelstrecke
- Sind für eine besondere Regelstrecke Spezialregler erforderlich, z. B. Kompensation der Störgröße, Kompensation der Totzeit, Vorsteuerungen zur Vermeidung von Folgefehlern, Regler für Mehrgrößensysteme,
- Welcher Einfluss der inneren Störgrößen der Hardware (alterungsbedingter Einfluss der Bauteile, Drift, Hysterese, Reibungseffekte usw.) ist in der gesamten Regeleinrichtung zugelassen.
Berufsverbände mit Bezug zur Regelungstechnik[Bearbeiten | Quelltext bearbeiten]
Deutschland:
International:
- International Federation of Automatic Control (IFAC)
- Institute of Electrical and Electronics Engineers (IEEE)
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Regelungstheorie
- Control in the Field
- Faustformelverfahren (Automatisierungstechnik)
- Modellprädiktive Regelung
- Fehlertolerantes Regelsystem
- Adaptive Regelung
- Optimale Regelung
- Automatisierung
Literatur[Bearbeiten | Quelltext bearbeiten]
- Adolf Leonhard: Die selbsttätige Regelung in der Elektrotechnik. J. Springer, Berlin 1940.
- Adolf Leonhard: Die selbsttätige Regelung. Theoretische Grundlagen mit praktischen Beispielen. Springer, Berlin; Göttingen; Heidelberg 1949, 2. Auflage 1957, 3. Auflage 1962, ISBN 978-3-642-92841-3.
- Otto Föllinger: Regelungstechnik. Hüthig Verlag, ISBN 3-7785-2336-8.
- Martin Horn, Nicolaos Dourdoumas: Regelungstechnik. Pearson Studium, 2006, ISBN 3-8273-7260-7.
- Ulrich Korn, Ulrich Jumar: PI-Mehrgrößenregler – praxisgerechter Entwurf, Robustheit, Anwendung. Oldenbourg Verlag, München, Wien 1991, ISBN 3-486-21720-8.
- Rolf Isermann: Identifikation dynamischer Systeme. Band 1 und 2. Springer Verlag, 1992, ISBN 3-540-55468-8.
- Lennart Ljung: System Identification – Theory for the User. Prentice Hall, ISBN 0-13-656695-2.
- Jan Lunze: Regelungstechnik 1. 6. Auflage. Springer Verlag, Berlin 2007, ISBN 978-3-540-70790-5. Regelungstechnik 2. 4. Auflage. Springer Verlag, Berlin 2006, ISBN 978-3-540-32335-8.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6.
- Heinz Mann, Horst Schiffelgen, Rainer Froriep,: Einführung in die Regelungstechnik. Carl Hanser Verlag, München 2009, ISBN 978-3-446-41765-6.
- Winfried Oppelt: Kleines Handbuch technischer Regelvorgänge. 5. Auflage. Verlag Chemie, Weinheim 1972, ISBN 3-527-25347-5.
- Kurt Reinschke: Lineare Steuerungs- und Regelungstheorie. Springer Verlag, Dresden 2005, ISBN 3-540-21886-6.
- Gerd Schulz: Regelungstechnik. Oldenbourg Verlag, 2002, ISBN 3-486-25858-3.
- Karl-Dieter Tieste: Keine Panik vor Regelungstechnik. Vieweg Verlag, 2011, ISBN 978-3-8348-0850-9.
- Heinz Unbehauen: Regelungstechnik. Band 1. Vieweg Verlag, Braunschweig 2005, ISBN 3-528-93332-1.
- Heinz Unbehauen: Regelungstechnik. Band 2. Vieweg Verlag, Braunschweig 2000, ISBN 3-528-73348-9.
- Heinz Unbehauen: Regelungstechnik. Band 3. Vieweg Verlag, Braunschweig 2011, ISBN 978-3-8348-1419-7.
- Josef Uphaus: Regelungstechnik. Bildungsverlag Eins, 2005, ISBN 3-427-44510-0.
- samson.de (Hrsg.): Begriffe und Symbole der Regelungstechnik. (samson.de [PDF]).
- Jürgen Adamy: Nichtlineare Regelungen. Springer Verlag, Berlin 2009, ISBN 978-3-642-00793-4.
- Werner Kriesel, Hans Rohr, Andreas Koch: Geschichte und Zukunft der Mess- und Automatisierungstechnik. VDI-Verlag, Düsseldorf 1995, ISBN 3-18-150047-X.
- Erwin Samal, Dirk Fabian, Christian Spieker: Grundriss der praktischen Regelungstechnik. Oldenbourg Verlag, 2013, ISBN 3-486-71290-X.
- Jörg Lange, Tatjana Lange: Fourier-Transformation zur Signal- und Systembeschreibung. Kompakt, visuell, intuitiv verständlich. Springer Vieweg 2019, ISBN 978-3-658-24849-9.
Zeitschriften und Journale:
- VDI/VDE-GMA, NAMUR [Interessengemeinschaft Prozessleittechnik der chemischen und pharmazeutischen Industrie] (Hrsg.): at – Automatisierungstechnik. Oldenbourg Wissenschaftsverlag (at-technik.de – monatlich seit 1953).
- atp – Automatisierungstechnische Praxis. Oldenbourg Wissenschaftsverlag, ISSN 0178-2320.
- atpi – Automation Technology in Practice. Oldenbourg Wissenschaftsverlag (englisch, oldenbourg-industrieverlag.de).
- MSR-Magazin. Zeitschrift für Messen, Steuern, Regeln. Verlag für Technik & Wirtschaft VTW (industrie-service.de).
- International Journal of Control. Taylor & Francis (englisch, tandf.co.uk).
- IFAC (Hrsg.): Automatica. Elsevier (englisch, elsevier.com).
- European Journal of Control. Elsevier (englisch, elsevier.com).
- Institution of Engineering and Technology [IET] (Hrsg.): IEE Proceedings – Control Theory & Applications. (englisch, ietdl.org).
- Norwegian Society of Automatic Control (Hrsg.): Modeling, Identification and Control. (englisch, itk.ntnu.no).
- Wroclaw University of Technology (Hrsg.): Systems Science. (englisch, Wroclaw UT).
- IEEE Control Systems Society [CSS] (Hrsg.): IEEE Control Systems Magazine. (englisch, web).
- IEEE Control Systems Society (Hrsg.): IEEE Transactions on Automatic Control. (englisch, ieeexplore.ieee.org).
- IEEE Control Systems Society (Hrsg.): IEEE Transactions on Control Systems Technology. (englisch, ieeexplore.ieee.org).
- ASME American Society Of Mechanical Engineers (Hrsg.): Journal of Dynamic Systems, Measurement, and Control. (englisch, scitation.aip.org).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Regelungstechnische Institute in Deutschland (Memento vom 2. Januar 2016 im Internet Archive)
- RoboterNetz Regelungstechnik
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Jürgen Müller: Regeln mit SIMATIC. Publicis Corporate Publishing, Erlangen 2004, ISBN 3-89578-248-3.
- ↑ Manfred Schleicher: Regelungstechnik für den Praktiker. Fa. JUMO GmbH & Co, 2006, ISBN 3-935742-00-2.
- ↑ Berthold Heinrich (Hrsg.): Messen, Steuern, Regeln. Vieweg Verlag, Wiesbaden 2005, ISBN 3-8348-0006-6.
- ↑ a b Hans-Joachim Zander: Steuerung ereignisdiskreter Prozesse. Neuartige Methoden zur Prozessbeschreibung und zum Entwurf von Steueralgorithmen. Springer Vieweg, Wiesbaden 2015, ISBN 978-3-658-01381-3 (323 S.).
- ↑ Hans-Peter Brill: Qualitätsmanagement für Software-Projekte: 10 der bekanntesten Software-Fehler. In: XING. 15. November 2007, abgerufen am 22. Juli 2019.
- ↑ Boeing räumt weiteres Softwareproblem ein. In: Spiegel Online. 5. April 2019, abgerufen am 22. Juli 2019.
- ↑ Ingo Pinter: Ex-Schutz per Pneumatik als Alternative zu elektrischen Geräten. In: Chemietechnik. 22. Juli 2010, abgerufen am 29. Juli 2019.
- ↑ Classic Honeywell Round Thermostat Teardown. (Video; 15:46 min) In: youtube. 4. Dezember 2016, abgerufen am 1. August 2019 (englisch, Zerlegung und Erklärung des Funktionsprinzips).
- ↑ Jan Lunze: Regelungstechnik. Teil 2: Mehrgrößensysteme, Digitale Regelung. 9. Auflage. Springer Vieweg, Berlin 2016, ISBN 978-3-662-52675-0 (720 S.).
- ↑ In dem Zeitungsartikel der Süddeutschen Zeitung vom 4. Februar 2013 unter „Wissen“ werden bezüglich Heizkostensparen durch Raumtemperaturabsenkung bei Abwesenheit im Haus unterschiedliche Ansichten des Umweltbundesamtes, die Gesellschaft „Initiative Wärme+“ und die halbstaatliche „Deutsche Energieagentur“ genannt. Ergebnis: Die Energieeinsparung durch kurzfristige Raumtemperaturabsenkung in einem gut gedämmten Haus ist viel geringer als in einem „Altbau“ mit weniger guter Dämmung. Bei Abwesenheit bis zu zwei Tagen können Absenkungen auf 18 °C nützlich sein. Ferner besteht bei größerer Absenkung die Gefahr der Kondensierung der Luftfeuchte mit Schimmelbildung.
- ↑ May-Britt Kallenrode, Universität Osnabrück, Fachbereich Physik: Vorlesungsmanuskript „Mathematik für Physiker“, Kapitel: „Differentialgleichungen“, ausgestellt 2007.
- ↑ Autor: Jan Lunze / Regelungstechnik 1; Kapitel: Totzeitsysteme: Auszug: „Totzeitsysteme können nicht mit dem Standard-Strukturbild des Zustandsraummodells beschrieben werden.“
- ↑ In der Fachliteratur und in den Vorlesungsmanuskripten der Hochschulen existieren keine einheitlichen Begriffe der Kennwerte. Deshalb Anlehnung an Fachbuchautoren: Holger Lutz, Wolfgang Wendt / Taschenbuch der Regelungstechnik: Kapitel: Zusammenhang zwischen Kenngrößen von Zeit- und Frequenzbereich.
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: Regelung durch Zustandsrückführung.







![Thermostat T86 von Honeywell, Design von Henry Dreyfuss (1953)[8]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1e/Honeywell_thermostat_open.jpg/140px-Honeywell_thermostat_open.jpg)
























![{\displaystyle [\theta _{\text{Heizkörpertemperatur - Raumtemperatur}}]=13{,}33\ +\ {\frac {40-13{,}33}{20}}\ \cdot \ [\theta _{\text{Raumtemperatur}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7e1dde8ff3c2acc2ea428c2d0ae5e1a0b2d8f4)