Matrizenmultiplikation

Bei einer Matrizenmultiplikation muss die Spaltenzahl der ersten Matrix gleich der Zeilenzahl der zweiten Matrix sein. Das Matrizenprodukt hat dann die Zeilenzahl der ersten und die Spaltenzahl der zweiten Matrix.

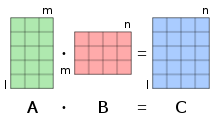
Die Matrizenmultiplikation oder Matrixmultiplikation ist in der Mathematik eine wichtige Verknüpfung von Matrizen. Um zwei Matrizen miteinander multiplizieren zu können, muss die Spaltenzahl der ersten Matrix mit der Zeilenzahl der zweiten Matrix übereinstimmen. Das Ergebnis einer Matrizenmultiplikation wird dann Matrizenprodukt oder Matrixprodukt genannt. Das Matrizenprodukt ist wieder eine Matrix, deren Einträge durch komponentenweise Multiplikation und Summation der Einträge der entsprechenden Zeile der ersten Matrix mit der entsprechenden Spalte der zweiten Matrix ermittelt werden.

Die Matrizenmultiplikation ist assoziativ und mit der Matrizenaddition distributiv. Sie ist jedoch nicht kommutativ, das heißt die Reihenfolge der Matrizen darf bei der Produktbildung nicht vertauscht werden. Die Menge der quadratischen Matrizen mit Elementen aus einem Halbring bildet zusammen mit der Matrizenaddition und der Matrizenmultiplikation den Halbring der quadratischen Matrizen. Weiter bildet die Menge der regulären Matrizen über einem unitären Ring mit der Matrizenmultiplikation die allgemeine lineare Gruppe. Matrizen, die durch spezielle Multiplikationen mit regulären Matrizen ineinander überführt werden können, bilden darin Äquivalenzklassen.

Der Standardalgorithmus zur Multiplikation zweier quadratischer Matrizen weist eine kubische Laufzeit auf. Zwar lässt sich der asymptotische Aufwand mit Hilfe spezieller Algorithmen verringern, die Ermittlung optimaler oberer und unterer Komplexitätsschranken für die Matrizenmultiplikation ist jedoch noch Gegenstand aktueller Forschung.

Die Matrizenmultiplikation wird häufig in der linearen Algebra verwendet. So wird beispielsweise die Faktorisierung einer Matrix als Produkt von Matrizen mit speziellen Eigenschaften bei der numerischen Lösung linearer Gleichungssysteme oder Eigenwertprobleme eingesetzt. Weiterhin ist die Abbildungsmatrix der Hintereinanderausführung zweier linearer Abbildungen gerade das Matrizenprodukt der Abbildungsmatrizen dieser Abbildungen. Anwendungen der Matrizenmultiplikation finden sich unter anderem in der Computergrafik, der Optik, der Elektrotechnik und der Ökonomie.

Die Matrizenmultiplikation wurde erstmals von dem französischen Mathematiker Jacques Philippe Marie Binet im Jahr 1812 beschrieben.

Definition

Zur Berechnung des Matrizenprodukts wird das Schema Zeile mal Spalte angewandt.

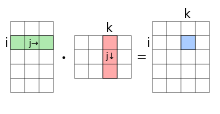
Die Matrizenmultiplikation ist eine binäre Verknüpfung auf der Menge der Matrizen über einem Halbring $R$ (oft der Körper der reellen Zahlen), also eine Abbildung

$\cdot ~\colon R^{l\times m}\times R^{m\times n}\to R^{l\times n},\quad (A,B)\mapsto C=A\cdot B$,

die zwei Matrizen $A=(a_{ij})$ und $B=(b_{jk})$ eine weitere Matrix $C=(c_{ik})$ zuordnet. Die Matrizenmultiplikation ist dabei nur für den Fall definiert, dass die Spaltenzahl $m$ der Matrix $A$ mit der Zeilenzahl der Matrix $B$ übereinstimmt. Die Zeilenzahl $l$ der Ergebnismatrix $C$ entspricht dann derjenigen der Matrix $A$ und ihre Spaltenzahl $n$ derjenigen der Matrix $B$. Jeder Eintrag $c_{ik}$ des Matrizenprodukts berechnet sich dabei über

$c_{ik}=\sum _{j=1}^{m}a_{ij}\cdot b_{jk}$,

also durch komponentenweise Multiplikation der Einträge der $i$-ten Zeile von $A$ mit der $k$-ten Spalte von $B$ und durch Summation über alle diese Produkte. Häufig wird bei der Notation einer Matrizenmultiplikation der Malpunkt weggelassen und man schreibt kurz $AB$ statt $A\cdot B$.

Beispiel

Gegeben seien die beiden reellen Matrizen

$A={\begin{pmatrix}3&2&1\\1&0&2\end{pmatrix}}\in \mathbb {R} ^{2\times 3}$   und   $B={\begin{pmatrix}1&2\\0&1\\4&0\end{pmatrix}}\in \mathbb {R} ^{3\times 2}$.

Da die Matrix $A$ ebenso viele Spalten wie die Matrix $B$ Zeilen besitzt, ist die Matrizenmultiplikation $A\cdot B$ durchführbar. Nachdem $A$ zwei Zeilen und $B$ zwei Spalten hat, wird das Matrizenprodukt ebenfalls zwei Zeilen und Spalten aufweisen. Um das erste Matrixelement der Ergebnismatrix zu berechnen, betrachtet man die erste Zeile von $A$ und die erste Spalte von $B$. Nun multipliziert man die jeweils entsprechenden Einträge miteinander und summiert die Ergebnisse auf (die Sternchen stehen für noch nicht berechnete Elemente):

${\begin{pmatrix}\color {OliveGreen}3&\color {OliveGreen}2&\color {OliveGreen}1\\1&0&2\end{pmatrix}}\cdot {\begin{pmatrix}\color {Red}1&2\\\color {Red}0&1\\\color {Red}4&0\end{pmatrix}}={\begin{pmatrix}{\color {OliveGreen}3}\cdot {\color {Red}1}+{\color {OliveGreen}2}\cdot {\color {Red}0}+{\color {OliveGreen}1}\cdot {\color {Red}4}&\ast \\\ast &\ast \end{pmatrix}}={\begin{pmatrix}{\color {Blue}7}&\ast \\\ast &\ast \end{pmatrix}}$

Für das nächste Matrixelement in der ersten Zeile und zweiten Spalte betrachtet man entsprechend die erste Zeile von $A$ und die zweite Spalte von $B$:

${\begin{pmatrix}\color {OliveGreen}3&\color {OliveGreen}2&\color {OliveGreen}1\\1&0&2\end{pmatrix}}\cdot {\begin{pmatrix}1&\color {Red}2\\0&\color {Red}1\\4&\color {Red}0\end{pmatrix}}={\begin{pmatrix}7&{\color {OliveGreen}3}\cdot {\color {Red}2}+{\color {OliveGreen}2}\cdot {\color {Red}1}+{\color {OliveGreen}1}\cdot {\color {Red}0}\\\ast &\ast \end{pmatrix}}={\begin{pmatrix}7&{\color {Blue}8}\\\ast &\ast \end{pmatrix}}$

Dieses Schema setzt man nun mit dem Matrixelement in der zweiten Zeile und ersten Spalte fort:

${\begin{pmatrix}3&2&1\\\color {OliveGreen}1&\color {OliveGreen}0&\color {OliveGreen}2\end{pmatrix}}\cdot {\begin{pmatrix}\color {Red}1&2\\\color {Red}0&1\\\color {Red}4&0\end{pmatrix}}={\begin{pmatrix}7&8\\{\color {OliveGreen}1}\cdot {\color {Red}1}+{\color {OliveGreen}0}\cdot {\color {Red}0}+{\color {OliveGreen}2}\cdot {\color {Red}4}&\ast \end{pmatrix}}={\begin{pmatrix}7&8\\{\color {Blue}9}&\ast \end{pmatrix}}$

Schließlich langt man bei dem letzten Element in der zweiten Zeile und zweiten Spalte an:

${\begin{pmatrix}3&2&1\\\color {OliveGreen}1&\color {OliveGreen}0&\color {OliveGreen}2\end{pmatrix}}\cdot {\begin{pmatrix}1&\color {Red}2\\0&\color {Red}1\\4&\color {Red}0\end{pmatrix}}={\begin{pmatrix}7&8\\9&{\color {OliveGreen}1}\cdot {\color {Red}2}+{\color {OliveGreen}0}\cdot {\color {Red}1}+{\color {OliveGreen}2}\cdot {\color {Red}0}\end{pmatrix}}={\begin{pmatrix}7&8\\9&{\color {Blue}2}\end{pmatrix}}$

Als Ergebnis erhält man am Ende das Matrizenprodukt $A\cdot B$. Eine alternative Möglichkeit zur Berechnung des Matrizenprodukts bietet das falksche Schema.

Spezialfälle

Zeilenvektor mal Spaltenvektor

Multiplikation eines Zeilenvektors mit einem Spaltenvektor

Besteht die erste Matrix aus nur einer Zeile und die zweite Matrix aus nur einer Spalte, so ergibt das Matrizenprodukt eine $(1\times 1)$-Matrix. Interpretiert man eine einzeilige Matrix als Zeilenvektor $x^{T}$ und eine einspaltige Matrix als Spaltenvektor $y$, so erhält man im Fall reeller Vektoren das Standardskalarprodukt

$\langle x,y\rangle =x^{T}\cdot y$

zweier Vektoren, wobei $x^{T}$ den zu $x$ transponierten Vektor darstellt, beide Vektoren gleich lang sein müssen und das Ergebnis dann eine reelle Zahl ist. Jeder Eintrag eines reellen Matrizenprodukts $A\cdot B$ kann somit als Skalarprodukt eines (Zeilen-)Vektors der Matrix $A$ mit einem (Spalten-)Vektor der Matrix $B$ angesehen werden.

Spaltenvektor mal Zeilenvektor

Multiplikation eines Spaltenvektors mit einem Zeilenvektor

Besteht umgekehrt die erste Matrix aus nur einer Spalte der Länge $m$ und die zweite Matrix aus nur einer Zeile der Länge $n$, so ergibt das Matrizenprodukt eine $(m\times n)$-Matrix. Interpretiert man wieder eine einspaltige Matrix als Spaltenvektor $x$ und eine einzeilige Matrix als Zeilenvektor $y^{T}$, so nennt man das entstehende Produkt von Vektoren dyadisches Produkt

$x\otimes y=x\cdot y^{T}$.

Jeder Eintrag $c_{ij}$ der resultierenden Matrix ist dabei das Produkt eines Elements $x_{i}$ des ersten Vektors mit einem Element $y_{j}$ des zweiten Vektors.

Matrix-Vektor-Produkt

Multiplikation einer Matrix mit einem Vektor

Ein wichtiger Spezialfall einer Matrizenmultiplikation entsteht, wenn die zweite Matrix aus nur einer Spalte besteht. Das Ergebnis der Matrizenmultiplikation ist dann ebenfalls eine einspaltige Matrix. Interpretiert man einspaltige Matrizen wieder als Spaltenvektoren, so heißt das entstehende Produkt Matrix-Vektor-Produkt

$A\cdot x=y$,

wobei $A\in R^{m\times n}$, $x\in R^{n}$ und $y\in R^{m}$ sind. Das Matrix-Vektor-Produkt wird beispielsweise in der Matrixschreibweise linearer Gleichungssysteme verwendet. Umgekehrt ergibt das Vektor-Matrix-Produkt aus einem Zeilenvektor und einer Matrix passender Größe wieder einen Zeilenvektor.

Quadrat einer Matrix

Wird eine quadratische Matrix $A\in R^{n\times n}$ mit sich selbst multipliziert erhält man wieder eine Matrix gleicher Größe, die als das Quadrat der Matrix bezeichnet wird, das heißt

$A^{2}=A\cdot A$.

Entsprechend dazu wird mit $A^{n}$ die Matrixpotenz, also das $n$-fache Produkt einer Matrix mit sich selbst, bezeichnet.

Blockmatrizen

Weisen die beiden Matrizen $A$ und $B$ eine Blockstrukturierung auf, wobei die Blockbreiten der ersten Matrix mit den Blockhöhen der zweiten Matrix übereinstimmen müssen, so lässt sich auch das Matrizenprodukt $A\cdot B$ blockweise notieren. Im Fall von jeweils zwei mal zwei Blöcken erhält man beispielsweise

${\begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}}\cdot {\begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{pmatrix}}={\begin{pmatrix}A_{11}B_{11}+A_{12}B_{21}&A_{11}B_{12}+A_{12}B_{22}\\A_{21}B_{11}+A_{22}B_{21}&A_{21}B_{12}+A_{22}B_{22}\end{pmatrix}}$.

Siehe auch: Blockmatrix#Multiplikation von Blockmatrizen

Eigenschaften

Assoziativität

Zur Berechnung eines Eintrags des Matrizenprodukts $\scriptstyle A\cdot B\cdot C$ werden alle Elemente der Matrix $\scriptstyle B$ benötigt (mittlere Zeile). Für die Bildung der hierbei benötigten Doppelsumme gibt es zwei Möglichkeiten (obere und untere Zeile).

Die Matrizenmultiplikation ist assoziativ, das heißt für Matrizen $A\in R^{l\times m}$, $B\in R^{m\times n}$ und $C\in R^{n\times o}$ gilt

$A\cdot (B\cdot C)=(A\cdot B)\cdot C$

Bei der Multiplikation mehrerer Matrizen ist es also unerheblich, in welcher Reihenfolge die Teilprodukte gebildet werden, solange die Gesamtreihung nicht verändert wird. Es gilt nämlich für einen Eintrag der so entstehenden Matrix $(d_{ih})\in R^{l\times o}$

${\begin{aligned}d_{ih}&=\sum _{j=1}^{m}a_{ij}\cdot \left(\sum _{k=1}^{n}b_{jk}\cdot c_{kh}\right)=\sum _{j=1}^{m}\sum _{k=1}^{n}a_{ij}\cdot b_{jk}\cdot c_{kh}=\\&=\sum _{k=1}^{n}\sum _{j=1}^{m}a_{ij}\cdot b_{jk}\cdot c_{kh}=\sum _{k=1}^{n}\left(\sum _{j=1}^{m}a_{ij}\cdot b_{jk}\right)\cdot c_{kh}.\end{aligned}}$

Die Matrizenmultiplikation ist auch verträglich mit der Multiplikation von Skalaren $a\in R$, das heißt

$a\cdot (B\cdot C)=(a\cdot B)\cdot C=B\cdot (a\cdot C)$.

Distributivität

Betrachtet man neben der Matrizenmultiplikation auch noch die komponentenweise Matrizenaddition $A+B$ zweier Matrizen $A,B\in R^{l\times m}$, dann sind auch die Distributivgesetze erfüllt, das heißt für alle Matrizen $C\in R^{m\times n}$ gilt

$(A+B)\cdot C=A\cdot C+B\cdot C$.

Entsprechend dazu gilt für alle Matrizen $C\in R^{n\times l}$

$C\cdot (A+B)=C\cdot A+C\cdot B$.

Die Distributivität folgt dabei direkt aus der Distributivität der Addition und Multiplikation im Halbring $R$.

Nichtkommutativität

Die Matrizenmultiplikation ist jedoch nicht kommutativ, das heißt für $A\in R^{m\times n}$ und $B\in R^{n\times m}$ ist im Allgemeinen

$A\cdot B\neq B\cdot A$.

Für die beiden Matrizenprodukte gilt nämlich $A\cdot B\in R^{m\times m}$ und $B\cdot A\in R^{n\times n}$, womit sie für $m\neq n$ schon von den Dimensionen her nicht übereinstimmen können. Aber selbst wenn $A$ und $B$ quadratisch sind müssen beiden Matrizenprodukte nicht gleich sein, wie das Gegenbeispiel

${\begin{pmatrix}0&2\\0&0\end{pmatrix}}\cdot {\begin{pmatrix}0&0\\2&0\end{pmatrix}}={\begin{pmatrix}4&0\\0&0\end{pmatrix}}\neq {\begin{pmatrix}0&0\\0&4\end{pmatrix}}={\begin{pmatrix}0&0\\2&0\end{pmatrix}}\cdot {\begin{pmatrix}0&2\\0&0\end{pmatrix}}$

zeigt. Die Nichtkommutativität der Matrizenmultiplikation gilt demnach sogar wenn die Multiplikation im Halbring $R$ kommutativ sein sollte, wie es beispielsweise bei Zahlen der Fall ist.

Weitere Rechenregeln

Für die Transponierte eines Matrizenprodukts gilt

$(A\cdot B)^{T}=B^{T}\cdot A^{T}$.

Die Reihenfolge bei der Multiplikation wird durch die Transposition also vertauscht. Für die Adjungierte des Produkts komplexer Matrizen gilt entsprechend

$(A\cdot B)^{H}=B^{H}\cdot A^{H}$.

Die Spur des Produkts zweier Matrizen $A\in R^{m\times n}$ und $B\in R^{n\times m}$ ist hingegen unabhängig von der Reihenfolge:

$\operatorname {spur} (A\cdot B)=\operatorname {spur} (B\cdot A)$.

Gleiches gilt auch für die Determinante des Produkts zweier quadratischer Matrizen über einem kommutativen Ring:

$\operatorname {det} (A\cdot B)=\operatorname {det} (B\cdot A)$.

Die Determinante des Produkts zweier nicht notwendigerweise quadratischer Matrizen kann mit dem Satz von Binet-Cauchy berechnet werden.

Algebraische Strukturen

Halbring der quadratischen Matrizen

Die Menge der quadratischen Matrizen bildet zusammen mit der Matrizenaddition und der Matrizenmultiplikation einen nichtkommutativen Halbring $(R^{n\times n},+,\cdot )$. Das Nullelement dieses Halbrings ist die Nullmatrix $0\in R^{n\times n}$. Wenn die Null in $R$ absorbierend ist, fungiert die Nullmatrix auch als absorbierendes Element, das heißt für alle Matrizen $A\in R^{n\times n}$ gilt

$A\cdot 0=0\cdot A=0$.

Der Halbring der quadratischen Matrizen ist, wenn die Null in $R$ absorbierend ist, nicht nullteilerfrei, denn aus $A\cdot B=0$ folgt nicht notwendigerweise $A=0$ oder $B=0$. Entsprechend darf bei Matrixgleichungen auch nicht gekürzt werden, denn aus $A\cdot B=A\cdot C$ folgt nicht notwendigerweise $B=C$. Ist $R$ ein unitärer Ring, dann ist auch der zugehörige Matrizenring unitär, wobei das Einselement durch die Einheitsmatrix $I\in R^{n\times n}$ dargestellt wird. Für die Einheitsmatrix gilt damit für alle $A\in R^{n\times n}$

$A\cdot I=I\cdot A=A$.

Gruppe der regulären Matrizen

Die Menge der regulären Matrizen $A\in R^{n\times n}$ über einen unitären Ring $R$ bildet mit der Matrizenmultiplikation die allgemeine lineare Gruppe $\operatorname {GL} (n,R)$. Die zur Matrix $A$ inverse Matrix ist dann eindeutig über

$A\cdot A^{-1}=A^{-1}\cdot A=I$

definiert. Für die Inverse des Produkts zweier regulärer Matrizen gilt dann

$(A\cdot B)^{-1}=B^{-1}\cdot A^{-1}$.

Durch die Invertierung wird die Reihenfolge bei der Multiplikation demnach ebenfalls vertauscht.

Gruppen der orthogonalen und unitären Matrizen

Eine reelle quadratische Matrix $A\in \mathbb {R} ^{n\times n}$ heißt orthogonal, wenn

$A\cdot A^{T}=A^{T}\cdot A=I$

gilt. Die orthogonalen Matrizen bilden mit der Matrizenmultiplikation die orthogonale Gruppe $\operatorname {O} (n)$, eine Untergruppe der allgemeinen linearen Gruppe $\operatorname {GL} (n,\mathbb {R} )$. Entsprechend dazu heißt eine komplexe quadratische Matrix $A\in \mathbb {C} ^{n\times n}$ unitär, wenn

$A\cdot A^{H}=A^{H}\cdot A=I$

gilt. Die unitären Matrizen bilden mit der Matrizenmultiplikation die unitäre Gruppe $\operatorname {U} (n)$, eine Untergruppe der allgemeinen linearen Gruppe $\operatorname {GL} (n,\mathbb {C} )$.

Äquivalenzklassen von Matrizen

Mit Hilfe der Matrizenmultiplikation werden Äquivalenzrelationen zwischen Matrizen über einem Körper definiert. Wichtige Äquivalenzrelationen sind:

• Äquivalenz: Zwei Matrizen $A$ und $B$ heißen äquivalent, wenn es zwei reguläre Matrizen $C$ und $D$ gibt, sodass $B=C^{-1}\cdot A\cdot D$ gilt.
• Ähnlichkeit: Zwei quadratische Matrizen $A$ und $B$ heißen ähnlich, wenn es eine reguläre Matrix $C$ gibt, sodass $B=C^{-1}\cdot A\cdot C$ gilt.
• Kongruenz: Zwei quadratische Matrizen $A$ und $B$ heißen kongruent, wenn es eine reguläre Matrix $C$ gibt, sodass $B=C^{T}\cdot A\cdot C$ gilt.

Matrizen, die durch solche Multiplikationen mit regulären Matrizen ineinander überführt werden können, bilden demnach Äquivalenzklassen.

Algorithmen

Standardalgorithmus

In Pseudocode kann die Matrizenmultiplikation wie folgt implementiert werden:

function matmult(A,B,l,m,n)
    C = zeroes(l,n)                                  // Ergebnismatrix C mit Nullen initialisieren
    for i = 1 to l                                   // Schleife über die Zeilen von C
        for k = 1 to n                               // Schleife über die Spalten von C
            for j = 1 to m                           // Schleife über die Spalten von A / Zeilen von B
                C(i,k) = C(i,k) + (A(i,j) * B(j,k))  // Bildung der Produktsumme
            end
        end
    end
    return C

Die Reihenfolge der drei For-Schleifen kann dabei beliebig vertauscht werden. Da die drei Schleifen unabhängig voneinander sind, ist die Anzahl der benötigten Operationen von der Ordnung

$O(l\cdot m\cdot n)$.

Die Laufzeit des Algorithmus ist demnach für quadratische Matrizen $(l=m=n)$ kubisch, also von der Ordnung

$O(n^{3})$.

Bei der Matrix-Kettenmultiplikation, also der Multiplikation von drei oder mehr nichtquadratischen Matrizen, kann durch eine geschickte Wahl der Reihenfolge die Gesamtzahl arithmetischer Operationen minimiert werden.

Algorithmen mit besserer Komplexität

Entwicklung der oberen Komplexitätsschranke der Matrizenmultikation in den letzten Jahrzehnten

Asymptotisch effizienter lassen sich zwei Matrizen mit dem Strassen-Algorithmus multiplizieren. Hierbei wird die Anzahl der Multiplikationen, die zur Multiplikation zweier $(2\times 2)$-Matrizen benötigt werden, durch geschicktes Zusammenfassen von acht auf sieben reduziert, was auf Kosten zusätzlicher Additionen geschieht. Wendet man dieses Verfahren rekursiv an, ergibt sich eine Komplexitätsordnung von

$O(n^{\log _{2}7})\approx O(n^{2{,}807})$.

Allerdings lohnt sich der Strassen-Algorithmus aufgrund der in der Landau-Notation versteckten Konstanten nur für sehr große Matrizen. Der Algorithmus mit der derzeit besten Komplexität ist eine Verbesserung des Coppersmith–Winograd-Algorithmus mit einer Laufzeit der näherungsweisen Ordnung

$O(n^{2{,}3727})$.

Für den praktischen Einsatz ist dieser Algorithmus jedoch nicht geeignet. Eine untere Schranke für die Komplexität der Matrizenmultiplikation ist

$\Omega (n^{2})$,

da jedes der $n^{2}$ Elemente der Ausgabematrix erzeugt werden muss. Die Ermittlung optimaler unterer und oberer Komplexitätsschranken für die Matrizenmultiplikation ist Gegenstand aktueller Forschung.

Verwendung

Faktorisierungen

Auf gewisse Weise die Umkehrung der Matrizenmultiplikation ist die Faktorisierung einer gegebenen Matrix $A$ als Produkt zweier Matrizen $B$ und $C$, das heißt die Ermittlung einer Darstellung der Form

$A=B\cdot C$.

Eine solche Faktorisierung ist nicht eindeutig, daher werden an die Matrizen $B$ und $C$ zusätzliche Anforderungen gestellt, wie Orthogonalität, Symmetrie oder eine bestimmte Besetzungsstruktur. Wichtige Zerlegungen reeller oder komplexer Matrizen dieser Art sind:

• die LR-Zerlegung einer quadratischen Matrix in eine untere und eine obere Dreiecksmatrix
• die Cholesky-Zerlegung, eine spezielle LR-Zerlegung einer symmetrisch positiv definiten Matrix
• die ILU-Zerlegung, eine Art unvollständige LR-Zerlegung speziell für dünnbesetzte Matrizen
• die QR-Zerlegung einer Matrix in eine orthogonale Marix und eine obere Dreiecksmatrix
• die Schurzerlegung einer quadratischen Matrix in drei Matrizen: eine unitäre Matrix, eine obere Dreiecksmatrix und die Inverse der ersten Matrix
• die Singulärwertzerlegung einer Matrix in drei Matrizen: eine unitäre Matrix, eine Diagonalmatrix bestehend aus den Singulärwerten und die Adjungierte einer unitären Matrix

Solche Zerlegungen von Matrizen werden häufig in der numerischen linearen Algebra etwa zur Lösung linearer Gleichungssysteme oder Eigenwertprobleme eingesetzt. So lassen sich beispielsweise die Zeilen- und Spaltenumformungen im gaußschen Eliminationsverfahren als Produkt von Elementarmatrizen angeben.

Komposition linearer Abbildungen

Hintereinanderausführung zweier linearer Abbildungen als Matrizenmultiplikation

Sind allgemein $V$ und $W$ zwei endlichdimensionale Vektorräume über dem gleichen Körper, dann kann jede lineare Abbildung $f\colon V\to W$ nach Wahl je einer Basis in den beiden Vektorräumen über ihre Abbildungsmatrix $M_{f}$ dargestellt werden. Das Bild $y$ eines Vektors $x$ unter der Abbildung $f$ in den jeweiligen Basen kann dann über das Matrix-Vektor-Produkt

$y=M_{f}\cdot x$

ermittelt werden. In der Geometrie lässt sich beispielsweise auf diese Weise jede Drehung um den Ursprung und jede Spiegelung an einer Ursprungsebene durch ein solches Matrix-Vektor-Produkt ausführen. Ist nun $U$ ein weiterer Vektorraum und $g\colon W\to U$ eine weitere lineare Abbildung, dann gilt für die Abbildungsmatrix der Hintereinanderausführung $g\circ f$ dieser beiden Abbildungen

$M_{g\circ f}=M_{g}\cdot M_{f}$.

Die Abbildungsmatrix einer Hintereinanderausführung zweier linearer Abbildungen ist also das Matrizenprodukt der beiden zugehörigen Abbildungsmatrizen. Auf diese Weise lässt sich beispielsweise jede Drehspiegelung als Produkt einer Drehmatrix und einer Spiegelungsmatrix darstellen.

Komposition differenzierbarer Funktionen

Sind $f\colon \mathbb {R} ^{k}\to \mathbb {R} ^{l}$ und $g\colon \mathbb {R} ^{l}\to \mathbb {R} ^{m}$ zwei differenzierbare Funktionen, so ist auch ihre Verkettung $g\circ f\colon \mathbb {R} ^{k}\to \mathbb {R} ^{m}$ differenzierbar. Die Ableitung der Verkettung in einem Punkt $x\in \mathbb {R} ^{k}$ ist nach der verallgemeinerten Kettenregel dann die Hintereinanderausführung der Ableitung von $f$ im Punkt $x$ und der Ableitung von $g$ im Punkt $f(x)$. Für die zugehörigen Jacobi-Matrizen gilt damit

$J_{g\circ f}(x)=J_{g}(f(x))\cdot J_{f}(x)$.

Die Jacobi-Matrix der Verkettung zweier differenzierbarer Funktionen ist also das Matrizenprodukt von Jacobi-Matrizen der beiden Funktionen.

Komposition von Relationen

Distributive Verbände, wie beispielsweise boolesche Algebren, sind Halbringe. Fasst man ihre Elemente als Wahrheitswerte auf, sind Matrizen über ihnen zweistellige Relationen. Die Matrizenmultiplikation entspricht in dem Fall der Komposition von Relationen.

Anwendungen

Anwendungen der Matrizenmultiplikation finden sich unter anderem:

• in der Computergrafik bei der Durchführung von Koordinatentransformationen in einer Grafikpipeline
• in der Optik bei der Berechnung von Lichtstrahlen durch optische Bauelemente mittels der Matrizenoptik
• in der Ökonomie bei der Input-Output-Analyse einer Produktion
• in der Elektrotechnik bei der Zweitortheorie elektrischer Netzwerke

Siehe auch: Matrixpotenz#Anwendungen

Verwandte Produkte

Neben dem Matrizenprodukt existieren noch eine Reihe weiterer Produkte von Matrizen:

• Das Hadamard-Produkt ist für zwei Matrizen gleicher Größe definiert und ergibt wieder eine Matrix derselben Größe, deren Einträge einfach durch komponentenweise Multiplikation der Einträge der Ausgangsmatrizen entstehen. Im Vergleich zum Matrizenprodukt ist es allerdings weit weniger bedeutend.

• Das Kronecker-Produkt ist für beliebige Matrizen definiert und liefert als Resultat eine große Matrix, die durch Betrachtung aller möglichen Produkte von Einträgen der beiden Ausgangsmatrizen entsteht.

• Das Hilbert-Schmidt-Skalarprodukt ist für gleich große Matrizen über den reellen oder komplexzen Zahlen definiert und liefert als Resultat eine reelle oder komplexe Zahl. Das Hilbert-Schmidt-Skalarprodukt entsteht durch komponentenweise Multiplikation der Einträge der Ausgangsmatrizen und nachfolgende Summation über all diese Produkte. Im komplexen Fall wird dabei immer ein Element komplex konjugiert.

Literatur

• Michael Artin: Algebra. Springer, 1998, ISBN 3-7643-5938-2. 
• Charles Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – eine Einführung. Oldenbourg, 2010, ISBN 3-486-59002-2. 
• Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 2. Auflage. Spektrum Akademischer Verlag, 2011, ISBN 3-8274-2347-3. 

Weblinks

• Eric W. Weisstein: Matrix Multiplication. In: MathWorld (englisch).
• djao: Matrix operations. In: PlanetMath. (englisch)
• Matrixmultiplikation Online Rechner