Benutzer:Googolplexian1221/Vermutung von Birch und Swinnerton Dyer
Die Vermutung von Birch und Swinnerton-Dyer, kurz BSD, ist eines der bedeutensten ungelösten Probleme der modernen Mathematik und macht Aussagen zur Zahlentheorie auf elliptischen Kurven. Benannt wurde sie nach den Mathematikern Bryan Birch und Peter Swinnerton-Dyer, die sie erstmals im Jahr 1962 aufstellten, wobei sie ihre Vermutung auf eine bereits 1958 gestartete Serie von Berechnungen an den EDSAC-Computern stützen. Diese hatten zum Ziel gehabt, eine mögliche und zur Klassenzahlformel von Dirichlet „analoge Theorie“ für elliptische Kurven zu entdecken. Die Vermutung wurde im Jahr 2000 vom Clay Mathematics Institute in die Liste der sieben Millennium-Probleme der Mathematik aufgenommen. Das Institut in Cambridge (Massachusetts) hat damit ein Preisgeld von einer Million US-Dollar für eine schlüssige Lösung des Problems in Form eines mathematischen Beweises ausgelobt. Hinsichtlich des Auffindens potenzieller Gegenbeispiele existieren in der Preisausschreibung jedoch Sonderregeln, insbesondere dann, wenn diese mit der Rechenkraft moderner Computer erlangt wurden, und keinerlei „tiefere Einsicht“ in das Problem geben können.
Die Vermutung von Birch und Swinnerton-Dyer ist für Mathematiker von großem Interesse, da sie eine überraschende und sehr tiefe Beziehung zwischen zwei völlig verschiedenen mathematischen Theorien aufbaut. Die Lösung des Problems würde demnach zwingend erfordern, bisher völlig unbekannte und äußerst tiefe Strukturen in der „Architektur der Mathematik“ an die Oberfläche zu fördern. Dabei hilft die Vorstellung, dass die Mathematik ein Gespinst aus zahllosen „Punkten“ (= Aussagen) ist, die durch „Pfeile“ (= logische Schlussfolgerungen) teilweise direkt miteinander verbunden sind. Brücken zwischen zwei vormals völlig verschiedenen Theorien helfen nun zahlreiche „neue Pfeile“ in diesem Graphen zu erhalten, was zur Folge hat, dass viele weitere Probleme gelöst werden können und einige neue Anwendungsmöglichkeiten entstehen. In diesem Kontext ist es nicht verwunderlich, dass gerade das Bauen solcher Brücken eine mathematisch besonders schwierige Aufgabe ist.
Trifft die Vermutung zu, existiert ein enger Zusammenhang zwischen den Lösungsanzahlen bestimmter Gleichungen und dem Nullstellenverhalten gewisser eben diesen Gleichungen zugehöriger mathematischen Funktionen. Die Lehre der Gleichungen ist dabei zentraler Gegenstand der Algebra. Von den Lösungen wird in der Formulierung des Problems jedoch verlangt, dass diese rationale Zahlen sind, also Quotienten ganzer Zahlen. Dies bringt neben der Algebra die mathematische Disziplin der Zahlentheorie mit ins Spiel. Im Gegensatz dazu sind mathematische Funktionen Teil der Analysis, die sich mit Aspekten wie Stetigkeit, Nullstellen und auch Differentialrechnung beschäftigt. Die große Herausforderung besteht also darin, diese völlig verschiedenen mathematischen Gebiete – Algebra, Zahlentheorie und Analysis – im Rahmen einer sehr schweren Fragestellung zu vereinen.
Mathematisch rigoros sagt das Problem: Sei eine nicht-singuläre elliptische Kurve über den rationalen Zahlen und ihre L-Funktion. Nach dem Satz von Mordell bildet die Menge aller rationalen Punkte die Struktur einer endlich erzeugten abelschen Gruppe, ist also isomorph zu , wobei den Torsionsteil von bezeichnet und der sog. Rang von ist. Die Vermutung sagt, dass gelten sollte.
Trotz immenser Anstrengungen ist man bis heute sehr weit von einer Lösung des Problems entfernt. Der Experte Andrew Wiles schätzt es als „nicht das einfachste Problem“ auf der Liste der Millennium-Probleme ein. Dennoch konnten im Laufe der Zeit Teilresultate für die Ränge und erzielt werden. Darüber hinaus existiert starke numerische Evidenz, die die Vermutung stützt und ihre Richtigkeit plausibel macht.
Problembeschreibung[Bearbeiten | Quelltext bearbeiten]
Die Vermutung von Birch und Swinnerton-Dyer sagt voraus, dass sich die Anzahlen der Lösungen zu gewissen Gleichungen an Stellen der modernen Mathematik wiederfinden lassen, wo man nicht mit ihnen rechnet. Dies ist gleichzeitig der Grund, weshalb sie als so schwer zu beweisen gilt: Bis heute verfügt die Menschheit über keine Theorie, die eine Erklärung für diesen Zusammenhang liefern kann. Mathematische Theorien sind auf Axiomen (= Grundannahmen) aufgebaut, die als wahr angenommen werden, aber trotzdem „einfach da sind“, und deshalb kommt es bis in die Gegenwart häufig vor, dass Probleme formuliert wurden, die erst weit nach Gründung der mathematischen Methodik gefunden oder gelöst wurden. Vergleichbar ist dies mit dem Schachspiel: Durch Angabe der einfachen Regeln ist das Spiel „vollständig vorhanden“, aber dennoch bis heute nicht „gelöst“ im dem Sinne, dass es keinen „perfekten Schachspieler“ gibt.


Zur Einordnung der Vermutung von Birch und Swinnerton-Dyer ist ein Verständnis des Konzepts der mathematischen Gleichung zentral. Beispiele für Gleichungen sind , und . Bei letzterer muss das Symbol erst „sichtbar“ gemacht werden, bevor mit endlich der einfache Zusammenhang klar erkannt wird. Gleichungen können umgeformt werden. Dahinter steckt die Idee, dass, wenn zwei identische Größen auf identische Weise manipuliert werden, die Resultate wieder identisch sein müssen. Addiert man beidseitig mit , entsteht daraus – wieder eine gültige Gleichung. Dividiert man beidseitig durch , entsteht , was den Vorteil hat, die schon vorher eindeutig bestimmte Größe „sichtbar“ gemacht zu machen. In vielen Problemen der wissenschaftlichen Praxis entstehen aus bekannten Beziehungen zunächst unbekannter Größen abstrakte Gleichungen, weshalb Techniken zu deren Auflösen große Bedeutung zukommt: Die innerhalb einer wissenschaftlichen Theorie erarbeiteten kausalen Zusammenhänge „zwingen“ die Größen in einen begrenzten Raum an Möglichkeiten, doch erst ein Auflösen der entstehenden Gleichungen macht diese wenigen Möglichkeiten „sichtbar“.
Die Vermutung beschäftigt sich mit Gleichungen ganz bestimmten Typs, die in der Mathematik – auch bezüglich ihrer Anwendungen – eine besondere Rolle einnehmen. Bezeichnet werden diese als elliptische Kurven. Streng genommen beschreibt das Wort „Gleichung“ diese aber nur unzureichend: Das Wort Kurve hingegen präzisiert, dass es sich bei einer elliptischen Kurve um eine Ansammlung aller Lösungen einer ganz bestimmten Gleichung mit zwei Unbekannten im Raum handelt, die als geometrische Figur eine „kurvenförmige“ Gestalt hat.
Dieses Konzept ist auch aus Sicht der Schulmathematik keinesfalls neu: Eine Gerade – Prototyp der „einfachsten“ aller Kurven – besteht aus allen Punkten , die gemeinsam eine Gleichung der Form
- mit festen Zahlen lösen (dabei werden die Komponenten und als Zahlen einzeln eingesetzt).
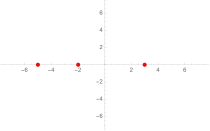
Dadurch, dass gleich zwei Größen, nämlich und , nicht näher benannt sind, ist eine größere Anzahl an Lösungen zu erwarten. Als Beispiel kann der Fall betrachtet werden: „Vollständig sichtbare“ Lösungen benennen beide Unbekannte, hier etwa , oder . Erst das Aufspannen zweier Dimensionen – also einer „x-Dimension“ und einer „y-Dimension“ – erlaubt es, dieses Kollektiv ganz zu fassen (siehe Bild 1). Wegen handelt es sich ferner um nichts anderes als eine tabellarische Auflistung aller Punkte der Form . Aus geometrischer Sicht ist es naheliegend, die daraus entstehende Kurve als Gerade zu bezeichnen.
Bei elliptischen Kurven handelt es sich hingegen um eine Ansammlung von Punkten , die gemeinsam eine kubische Gleichung erfüllen, die meist in der Form
- mit festen Zahlen
geschrieben wird. Die Zahlen und sind rational, und wegen deren Beliebigkeit gibt es eine „unendliche Familie“ elliptischer Kurven:
- und eine unbegrenzte Zahl weiterer Beispiele. Das Beispiel soll ab jetzt öfter für Veranschaulichungen herangezogen werden.
Wie im Falle der Geraden werden beim Aufbau elliptischer Kurven nur die vier Grundrechenarten genutzt. Daher werden sie, genauso wie die Geraden, zu den algebraischen Kurven gezählt. Wie bei allgemeinen Gleichungen kann man auch hier nach Lösungen fragen. Die Vermutung von Birch und Swinnerton-Dyer ist jedoch ein zahlentheoretisches Problem. Im Vordergrund des Interesses stehen also rationale Lösungen von Gleichungen, die dann zu Punkten etwa der Formen
- oder
korrespondieren. Man ist also ausschließlich an rationalen Punkten interessiert.

Beispiel: Es liegt der rationale Punkt (d.h. und ) auf der elliptischen Kurve , denn es gilt
- (auf beiden Seiten ist das Ergebnis ).
Dabei ist zu beachten, dass und analog . Ähnlich schnell lässt sich nachprüfen, dass die rationalen Punkte , , sowie auf der Kurve liegen.
Tatsächlich sind diese 5 Beispiele die einzigen rationalen Punkte auf der elliptischen Kurve , also wird keine Kombination rationaler Zahlen außer den oben genannten die Gleichung erfüllen.[1] Dies zu sehen ist jedoch mathematisch eine schwierige Aufgabe.
Die Vermutung von Birch und Swinnerton-Dyer beschäftigt sich mit der Anzahl rationaler Punkte auf elliptischen Kurven. Trifft sie zu, kann mit vergleichsweise wenig Aufwand „direkt ausgerechnet werden“, dass auf der Kurve nur endlich viele rationale Punkte liegen können.
Dies demonstriert, dass Punkte auf Kurven durch geschicktes Raten gefunden werden können – und der einfache Aufbau einer Kurve macht die Probe sehr leicht. Bloßes Raten ist im Allgemeinen allerdings kein akzeptabler mathematischer Algorithmus (= Vorgehensweise). Es gibt jedoch kein bewiesenes schnelles Verfahren, die Gleichungen einer elliptischen Kurve „aufzulösen“, also ohne naives Raten Punkte tatsächlich zu finden. Dafür ist in besonderem Maße der Term verantwortlich, der eine wesentliche Verkomplizierung der Gleichung zur Folge hat. Gerade aus zahlentheoretischer Sicht sind algebraische Kurven, die aus den vier Grundrechenarten hervorgehen, allerdings von sehr großem Interesse: In den Gleichungen werden die Rechendisziplinen der Addition und der Multiplikation vermischt, wie man beim Weglassen der Abkürzungskonventionen besonders gut erkennen kann:
Jedoch verbirgt sich die äußerst tiefe Struktur „hinter den Zahlen“ gerade in einem „möglichen Zusammenspiel“ aus Addition und Multiplikation, und was zuerst simpel klingt, ist ein extrem schwieriges Problem. Einige prominente ungelöste mathematische Probleme demonstrieren dies:
- Es ist bis heute unbekannt, ob es unendlich oft vorkommt, dass zwei benachbarte Primzahlen den Abstand 2 haben. Beispiele für diese Primzahlzwillinge sind und . Primzahlen entspringen der multiplikativen Zahlentheorie, aber die Vorschrift, dass die Differenz den Wert haben soll, ist additiv.
- Die abc-Vermutung bringt Eigenschaften der Primfaktorenzerlegungen teilerfremder Zahlen und mit der von in Verbindung.
Vergleichbar ist die Tatsache, dass es die theoretische Physik bis heute nicht schafft, die Grundkräfte in einer großen vereinheitlichten Theorie zu einen.

Dem Problem des Auffindens von rationalen Lösungen algebraischer Gleichungen, wie etwa , stand die Mathematik viele Jahrhunderte ratlos gegenüber. Bei der Entwicklung und Etablierung moderner mathematischer Methoden kam man jedoch zu dem Schluss, dass es helfen kann, eine Gleichung wie als ein „System“ aufzufassen. Bei dessen Untersuchung hilft es, dieses in sehr viele kleine „Teilsysteme“ zu „zerlegen“ und diese „Einzelteile“ separat zu studieren. Gegebenenfalls sagen dann Muster in diesen lokalen Teilen etwas über das globale System aus. Die lokalen Untersysteme sind dabei im Wesentlichen wieder die Gleichung , aber mit dem Unterschied, dass es nur eine endliche Anzahl an Möglichkeiten für die Größen und zur Auswahl gibt. Diese endlich vielen Größen formen jedoch in Analogie zu den rationalen Zahlen wieder einen hinsichtlich der vier Grundrechenarten abgeschlossenen Bereich (so dass algebraische Gleichungen weiterhin einen Sinn ergeben). In der Zahlentheorie nennt man dieses Prozedere auch Lokal-Global-Prinzip.
Jedes „Teilsystem“ kann nun wegen des deutlich eingeschränkten „Definitionsbereichs“ für und einfacher analysiert werden. Zählt man dort die Lösungen (etwa über eine Computerberechnung), gewinnt man über diese Strategie ein Verfahren
- Teilsystem Ganze Zahl.
Daraus ergibt sich eine Folge ganzer Zahlen, die nicht endet (da es unendlich viele „Teilsysteme“ gibt). Etwa ergibt sich für den Fall
Aus diesen Zahlen kann man nun eine mathematische Funktion erzeugen (das im Index notiert, dass diese von der fest gewählten elliptischen Kurve abhängt). Dieser Konstruktionsprozess ist mathematisch keine einfache Aufgabe, wird aber in diesem Artikel weiter unten beschrieben. Zur Formulierung der Vermutung ist jedoch nur das Verhalten der Funktion an der Stelle entscheidend, weshalb ihr „Funktionsterm“ gar nicht genauer bekannt sein muss. Eine erste, sehr grobe Formulierung ist:
Trifft die Vermutung zu, sagt das Nullstellenverhalten von an etwas darüber aus, wie viele rationale Punkte die elliptische Kurve hat.
Dabei wird nicht bloß zwischen „endlich“ und „unendlich“ unterschieden, sondern es gibt sogar verschiedene Ausprägungen von unendlich – dies äußert sich in der Nullstellenordnung bei : Es bezeichnen
die Prototypen der Funktionen mit Nullstellenordnungen 0, 1, 2, 3, 4, usw. an der Stelle .
-
Keine Nullstelle entspricht Ordnung 0.
-
Exemplarisch ; Nullstelle erster Ordnung
-
Exemplarisch ; Nullstelle zweiter Ordnung
-
Exemplarisch ; Nullstelle dritter Ordnung
-
Ordnung Null entspricht nur endlich vielen Lösungen.
-
Bei erster Ordnung liegen die Lösungen schematisch auf einem „Strahl“ (eindimensional). Das angedeutete Muster setzt sich bis ins Unendliche fort.
-
Bei zweiter Ordnung liegen die Lösungen schematisch auf einer „Ebene“ (zweidimensional). Das angedeutete Muster setzt sich bis ins Unendliche fort.
-
Bei dritter Ordnung liegen die Lösungen schematisch im dreidimensionalen Raum. Das angedeutete Muster setzt sich bis ins Unendliche fort.
Dieses Muster setzt sich weiter fort, wobei ab Dimension 4 jedoch keine anschauliche Darstellung mehr möglich ist. Sehr wichtig ist zudem, dass dies nur exemplarische Darstellungen der Lösungen sind, also die Lösungen per se nicht Punkte in sehr hochdimensionalen Räumen sind – haben sie doch stets die Form . Diese Darstellung über eine „Gitterstruktur“ der Lösungen macht dennoch Sinn – und motiviert sich rechnerisch: Auf den rationalen Punkten elliptischer Kurven ist nämlich eine Form der „Addition“ erklärt. Es ist also möglich, über ein rechnerisches Verfahren
aus zwei bekannten Punkten und auf einer elliptischen Kurve einen neuen Punkt auf eben dieser zu gewinnen. Dieses Verfahren ist mühsam, beruht aber ausschließlich auf den vier Grundrechenarten. Hat man also zwei rationale Punkte durch geschicktes Raten gefunden, so kann man durch eine Rechenoperation einen dritten, möglicherweise völlig neuen, rationalen Punkt auf eben jener Kurve erzeugen. Eine Folgerung ist, dass viele „komplizierte Punkte“ auf der Kurve durch häufige „Addition“ oder „Subtraktion“ „simplerer Punkte“ entstehen, und so reicht es gewissermaßen aus, die „simplen Punkte“ zu zählen, um ein Verständnis für die Anzahl aller Punkte zu gewinnen. Dies motiviert die oben angedeutete Form der „Dimension“: Die Elemente und etwa erzeugen auf Ebene der klassischen Addition alle Punkte mit ganzen auf eindeutige Weise, zum Beispiel ist
Genauso muss auf Ebene der Punkte auf einer elliptischen Kurve gedacht werden: Gibt es genau zwei Punkte und , die im Wesentlichen alle anderen auf eindeutige Weise erzeugen, so entsteht gedanklich durch eine „P1“-Achse und „P2“-Achse ein zweidimensionales Gitter.
-
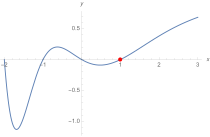
Schaubild der L-Funktion zu mit erkennbar keiner Nullstelle in .
-
Schaubild der L-Funktion zu . In liegt eine einfache Nullstelle vor (die x-Achse wird geschnitten und nicht berührt).
-
Schaubild der L-Funktion zu . Es liegt eine Nullstelle zweiter Ordnung in vor.
-
Schaubild der L-Funktion zu . Es liegt eine Nullstelle dritter Ordnung in vor.
-
Null „Erzeuger“; nur endlich viele rationale Punkte auf (siehe oberes Beispiel).
-
Genau ein „Erzeuger“, nämlich in dieser Graphik. Ein Punkt auf der Kurve erzeugt im Wesentlichen alle anderen rationalen Punkte.[2]
-
Zwei „Erzeuger“, nämlich und in dieser Graphik. Zwei Punkte und auf der Kurve erzeugen im Wesentlichen alle anderen rationalen Punkte.[3]
-
Drei „Erzeuger“, nämlich , und in dieser Graphik. Drei Punkte , und auf der Kurve erzeugen im Wesentlichen alle anderen rationalen Punkte.[4]
Der Ausdruck „im Wesentlichen“ bedeutet, dass es bei elliptischen Kurven stets endlich viele „Ausnahmepunkte“ geben kann, die sich „gänzlich“ nicht aus den Erzeugern generieren lassen. Genauer gesagt gibt es stets eine (sogar eindeutige) Zerlegung
Somit muss stets bis auf diese endlich vielen Ausnahmepunkte gedacht werden.
Vermutung von Birch und Swinnerton-Dyer: Die Nullstellenordnung der zur elliptischen Kurve zugeordneten mathematischen Funktion ist eine „Dimensionszahl“. Sie gibt exakt an, wie viele rationale Punkte man mindestens braucht, um im Wesentlichen alle anderen rationalen Punkte auf durch „Addition“ und „Subtraktion“ zu generieren.
Die Vermutung von Birch und Swinnerton-Dyer ist also eine Variante der Lokal-Global-Prinzips: Da alle lokalen Teilsysteme der elliptischen Kurve gleichzeitig die Funktion in ihrem „Zusammenspiel“ definieren, sollten diese der Lokal-Global-Philosophie folgend etwas über die Gleichung in den rationalen Zahlen wissen.
Ebenfalls offen ist die Frage, ob es überhaupt elliptische Kurven mit beliebig hohem Rang gibt. Bekannt ist die von Noam Elkies gefundene Kurve
mit Rang mindestens 28.
Die Existenz einer solchen merkwürdigen Art von Addition wird auch in den sogenannten „Elliptic-curve“-Primzahltests, in HW Lenstras „Elliptic-curve“-Faktorisierungsmethode und in „public-key“-Verschlüsselungsverfahren in der Kryptographie ausgenutzt. Dazu braucht man Kurven mit möglichst vielen rationalen Punkten und nutzt die Schwierigkeit aus, die Ausgangsdaten für die additive Erzeugung großer rationaler Punkte der Kurve zu finden. Siehe dazu Elliptische-Kurven-Kryptosysteme.
Benötigte Grundlagen und Formulierung[Bearbeiten | Quelltext bearbeiten]
Notation[Bearbeiten | Quelltext bearbeiten]
Es werden die folgenden üblichen Notationen verwendet:
- für die natürlichen Zahlen.
- für die ganzen Zahlen.
- für die rationalen Zahlen.
- für die reellen Zahlen.
- für die komplexen Zahlen. Es bezeichnen und den Real- bzw. Imaginärteil der komplexen Zahl .
- Es bedeutet , dass ein Element der Menge ist, und dass es kein Element der Menge ist. Zum Beispiel ist und .
- Es bezeichnet die natürliche Exponentialfunktion und den natürlichen Logarithmus.
Rechnen mit rationalen Zahlen[Bearbeiten | Quelltext bearbeiten]
Die Vermutung von Birch und Swinnerton-Dyer beschäftigt sich mit sog. rationalen Punkten. Für ein näheres Verständnis ist das Rechnen mit rationalen Zahlen bzw. „Brüchen“ also unverzichtbar. Eine reelle Zahl – anschaulich jede mögliche Länge auf einem Strahl ohne „kleinste Einheit“ – heißt rational, falls sie als Quotient zweier ganzer Zahlen geschrieben werden kann, also mit irgendwelchen ganzen Zahlen und . Dabei ist der Zähler und der Nenner. Beispiele für rationale Zahlen sind . Es handelt sich also anschaulich genau um jene Bruchteile, die entstehen, wenn eine „zählbare“ Anzahl von Dingen (wie „17 Euro“) auf eine ebenfalls „zählbare“ Personengruppe (zum Beispiel „4 Personen“) verteilt werden soll. Der entstehende Bruch kann dann als „Anteil für jede Person“ interpretiert werden.
Mit rationalen Zahlen kann gerechnet werden:
- Zwei Brüche werden addiert, indem man ihren gemeinsamen Nenner bildet. Dies ermöglicht eine einfache Addition über die Summation der Zähler. So liegt es etwa auf der Hand, dass 2 Siebtel und 8 Siebtel zusammengenommen 10 Siebtel ergeben, also . Anteile addieren sich effektiv wie das Zusammenlegen von zum Beispiel Kuchenstücken gleicher Größe. Für die Bildung des gemeinsamen Nenners werden Brüche erweitert: Es ist für den Bruchteil unerheblich, ob man zum Beispiel 2 Kuchen auf 4 Personen oder 4 Kuchen auf 8 Personen verteilt; in beiden Fällen erhält jede Person einen halben Kuchen, also . Diese Identitäten können bei der Addition von Brüchen helfen: Es gilt zum Beispiel . Ganz allgemein hat man . Die Subtraktion zweier Brüche erklärt sich analog.
- Zwei Brüche werden multipliziert, indem man Nenner und Zähler jeweils multipliziert. Dahinter verbirgt sich die Ermittlung des Bruchteils eines Bruchteils. „Nimmt“ man also eine Größe mit „mal“, übersetzt sich dies in
- „der Bruchteil von “.
- So ist zum Beispiel die Hälfte von einem Drittel ein Sechstel, also , und drei Viertel von zwei Ganzen drei Halbe, also . Dies ist ferner konform mit der Anschauung der Multiplikation durch eine ganze Zahl: So ist das Doppelte – hier als ein spezieller Bruchteil zu verstehen – einer Größe gerade „zwei mal“ diese Größe, also . Allgemein gilt . Ferner gleicht den „negativen Teil“ einer Größe zu nehmen der Multiplikation mit . Es lässt sich das universelle Gesetz wie folgt veranschaulichen: Der negative Teil von Schulden ist Guthaben, denn wer weniger als Null Schulden besitzt, ist „im Plus“.
- Da die Division „das Gegenteil“ der Multiplikation ist, impliziert sie Multiplikation mit dem Kehrwert bzw. Kehrbruch des Divisors. Wird eine Größe durch dividiert, ist sie also mit zu multiplizieren.
Nicht jede reelle Zahl ist rational, auch wenn Menschen dies lange vermuteten. Ein berühmtes Beispiel einer nicht-rationalen, also irrationalen, reellen Zahl ist die Kreiszahl:
Auch wenn es nicht möglich ist, die Kreiszahl als Quotient zweier ganzer Zahlen auszudrücken, kann sie wie jede andere reelle Zahl beliebig durch Brüche angenähert werden. So gilt zum Beispiel
- oder auch
Da die oben wiederholten Rechenregeln für all diese beliebig guten Näherungen gelten, lassen sie sich „im Grenzwert“ auch auf reelle Größen übertragen, behalten dort also auch Gültigkeit. Zum Beispiel gilt
Von sehr großer Bedeutung ist ebenfalls das Rechnen mit Potenzen. Diese werden durch einen Exponenten ausgedrückt, also eine „Hochzahl“, und zählen die Anzahl gleicher Faktoren. Etwa ist . Wegen der Rechenregeln für Brüche gilt allgemein .
Algebraische Kurven[Bearbeiten | Quelltext bearbeiten]

Der Begriff des Punkts spielt für die Vermutung von Birch und Swinnerton-Dyer eine wichtige Rolle. Besondere Bedeutung kommt hierbei dem Zusammenspiel zwischen dem örtlichen Aspekt eines Punktes (Geometrie) und dem quantitativen Aspekt (Zahlentheorie) zu. Anschaulich ist ein Punkt ein Objekt „ohne jede Ausdehnung“. In der Euklidischen Ebene kann ein Punkt stets durch Angabe kartesischer Koordinaten angegeben werden, man schreibt dann . Bei und handelt es sich um reelle Zahlen, und die Ebene wird dadurch definiert, dass man jede mögliche Kombination von Längen und zweier Zahlenstrahlen betrachtet. Diese Zahlenstrahlen lassen sich als zwei Achsen visualisieren, die die Ebene „aufspannen“ (siehe Bild).
Ein bedeutender Gegenstand der ebenen Geometrie ist das Studium von Figuren in der Ebene. Dazu zählen zum Beispiel Geraden, Kreise, Hyperbeln, Parabeln oder auch Ellipsen. All diese Figuren haben gemeinsam, dass sie aus einer Teilmenge aller Punkte der Ebene entstehen. Zum Beispiel ist jeder Punkt auf einem Kreis Teil der Ebene, aber nicht jeder Punkt der Ebene ist Teil des Kreises. Mehr noch: Gerade die explizite Auswahl bestimmter Punkte und deren „Zusammenwirken“ ergibt den Kreis. Entscheidend ist daher die Frage, nach welchen Kriterien man alle Punkte auf einer Figur bestimmen kann. Gleichbedeutend kann gefragt werden, in welcher Gemeinsamkeit sich die Punkte einer Figur von all den anderen Punkten in der Ebene unterscheiden.
Theoretisch lassen sich beliebig willkürliche „Figuren“ durch Auswahl völlig zufälliger Punkte formen – die Möglichkeiten sind unbegrenzt. Dennoch wird, angefangen in der Schulmathematik, gleich zu Beginn der Fokus auf ganz bestimmte Figuren gelegt, angefangen mit der Geraden. Ihre geometrische Natürlichkeit korrespondiert zur Algebra, denn die Gemeinsamkeit der Punkte auf einer Geraden kann mit den vier Grundrechenarten erklärt werden. Verläuft die Gerade nicht parallel zur „y-Achse“, so existieren stets zwei Zahlen und , so dass ihre Punkte sämtlich von der Gestalt sind. Da die zweite Koordinate traditionell als geschrieben wird, ist die (äquivalente) Beschreibung als Gleichung sehr gebräuchlich. Während in der Ebene bei der Wahl eines Punktes völlige Offenheit herrschte, ist die Geradenvorschrift mathematisch diskriminierend, denn durch die (freie) Auswahl der ersten Koordinate bleibt für die zweite Koordinate lediglich der Wert übrig, alle anderen „Kandidaten“ scheiden aus und sind nicht Teil der Geraden.
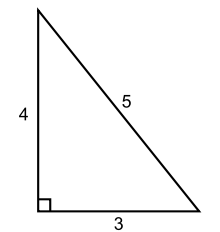
Eine algebraische Kurve ist nun allgemein eine Familie von Punkten in der Ebene, deren Komponenten und alle eine gemeinsame algebraische Relation erfüllen. Das bedeutet, dass es eine Gleichung gibt, in der ausschließlich endlich oft addiert, subtrahiert, multipliziert und dividiert wird, die von allen Punkten gleichzeitig erfüllt wird. Wie oben gesehen erfüllen die Punkte auf (den meisten) Geraden eine algebraische Relation mit festen Zahlen und . Aber auch algebraische Gleichungen höheren Grades sind möglich. Die Normalparabel besteht aus allen Punkten der Form , und der Kreis mit Radius 1 und dem Ursprung als Mittelpunkt besteht genau aus allen Punkten , sodass
gilt. Dies kann mit dem Satz des Pythagoras gezeigt werden (siehe Bild). Die Formulierung, dass eine Kurve über den rationalen Zahlen definiert sei, bedeutet ferner, dass alle involvierten Polynome zur Definition der Kurve ausschließlich rationale Zahlen verwenden.
-
Es gibt unzählige Möglichkeiten, Punkte (hier in Schwarz) aus der Ebene zu wählen. Was könnte eine „Gemeinsamtkeit“ all dieser Punkte sein?
-
Bei einer algebraischen Kurve haben alle ausgewählten Punkte eine grundrechnerische Gemeinsamkeit. Hier .
-
Jeder Punkt auf dem Einheitskreis induziert ein rechtwinkliges Dreieck mit Kathetenlängen und Hypotenusenlänge . Nach dem Satz des Pythagoras gilt demnach stets . Also ist auch der Kreis eine algebraische Kurve.
-
Schaubild der elliptischen Kurve
Bei einer elliptischen Kurve über den rationalen Zahlen handelt es sich um eine Kurve, deren Punkte eine Gleichung der Form
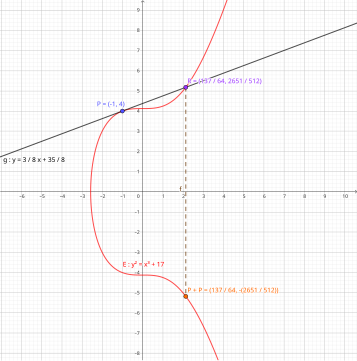
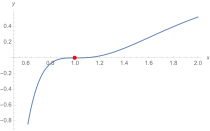
erfüllen. Bei handelt es sich um feste, also kurvenspezifische, rationale Zahlen. Dabei liegt das Augenmerk auf der dritten Potenz , die eine deutliche Verkomplizierung der Gleichung gegenüber quadratischen Kreisgleichungen mit sich bringt. Aus diesem Grund zählen elliptische Kurven nicht zu den linearen oder quadratischen Kurven, sondern sind kubische Kurven. Explizites Beispiel einer elliptischen Kurve über den rationalen Zahlen ist (siehe Bild).
Algebraische Kurven können in ihrem Ausmaß, etwa bezüglich des Grades der involvierten Polynome, beliebig kompliziert sein. Etwa definiert auch
eine algebraische Kurve. In manchen Fällen kann es helfen, mit einer Parametrisierung zu arbeiten. Damit ist eine Abbildung gemeint, die einem „isolierten“ Parameter einen Punkt auf der Kurve zuordnet. Ohne Mühe ist erkennbar, dass die Abbildungen bzw. Geraden bzw. die Normalparabel parametrisieren. Mit etwas mehr Aufwand kann gezeigt werden, dass
den Einheitskreis parametrisiert, denn es gilt , also mit den Rechenregeln für Brüche
Rationale Punkte[Bearbeiten | Quelltext bearbeiten]
Die gegenseitige Lage der Punkte auf einer Kurve sagt etwas über ihre Geometrie aus. Eine zunächst andere Frage geht in die Richtung der Eigenschaften ihrer Punkte. Die „Zahlentheorie auf einer Kurve“ etwa fragt, „wie viele“ rationale Punkte auf einer bestimmten Kurve liegen. Ein Punkt heißt dabei rational, falls beide Komponenten und rationale Zahlen sind, wie zum Beispiel .
Im Falle der Normalparabel, aber auch des Einheitskreises, sieht man über die Parametrisierungen bzw. recht schnell, dass unendlich viele rationale Punkte auf beiden Kurven liegen müssen. Wird der Parameter rational gewählt, so müssen die entsprechenden Punkte rational sein, da die rationalen Zahlen unter den vier Grundrechenarten abgeschlossen sind. Beispiel für einen rationalen Punkt auf dem Einheitskreis ist , denn es gilt
Multipliziert man beide Seiten mit , erhält man . Generell gibt es eine enge Korrespondenz zwischen rationalen Punkten auf dem Einheitskreis und sog. pythagoräischen Tripeln.
Falls eine algebraische Kurve über den rationalen Zahlen definiert ist, heißt das allerdings noch nicht, dass sie viele rationale Punkte haben muss. Allgemein ist es mathematisch ein sehr schweres Problem, zu entscheiden, welche rationalen Punkte auf einer Kurve über den rationalen Zahlen liegen, oder überhaupt irgendeinen solchen Punkt zu finden. Ein Grund dafür ist die Vermischung der Addition und Multiplikation, die beim Aufbau einer Kurve zwangsläufig entstehen kann, die sich aber im Allgemeinen nicht mehr „entwirren“ lässt. Einige Beispiele demonstrieren diese Problematik:
- Während lineare und quadratische Gleichungen einer Variablen elementar aufgelöst werden können, letztere mit der aus der Schulmathematik bekannten Mitternachtsformel, gibt es zum Beispiel für Gleichungen der Form (und auch höheren Grades) kein allgemeines Lösungsverfahren, bzw. keine Möglichkeit, die Lösungen ganz allgemein geschlossen durch Wurzelausdrücke zu schreiben.
- Während die Gleichung unendlich viele nicht-triviale ganze Lösungen besitzt, wie zum Beispiel oder , war es lange Zeit eine offene Frage, ob auch für mit ganzzahlige Lösungen mit existieren. Das Problem korrespondiert dabei – nach beidseitiger Division mit – zu den rationalen Punkten der algebraischen Kurven
- ,
- ,
- ,
- usw.
- Der Große Fermatsche Satz, der dies verneint, konnte erst Ende des 20. Jahrhunderts unter großen Anstrengungen gezeigt werden. Dabei wurde nicht die Gleichung umgeformt oder aufgelöst, etwa durch den wirkungslosen „Ansatz“ , sondern ein Resultat über elliptische Kurven bewiesen, die zu den Fermat-Gleichungen korrespondieren.
Die Mathematik ist an rationalen Punkten auf Kurven, trotz der damit einhergehenden immensen Schwierigkeiten, interessiert, da sich die tiefere Natur der Zahlen gerade durch ihr Zusammenspiel mit Addition und Multiplikation offenbart. Während die obige Situation von Kurven mit linearen bzw. quadratischen Polynomen einfach zu behandeln ist, gibt es für elliptische Kurven bis heute kein (bewiesenes) allgemeines Verfahren, um zu entscheiden, wie viele rationale Punkte auf ihr liegen. Die Vermutung von Birch und Swinnerton-Dyer gibt sehr grob gesprochen ein solches Verfahren an.
Die Diskriminante einer elliptischen Kurve[Bearbeiten | Quelltext bearbeiten]
In der Mathematik hilft es oft, komplizierten Objekten „Kennzahlen“ zuzuordnen. Diese sollen zum Beispiel dabei helfen, diese Objekte in ihrer Grundstruktur auseinanderzuhalten, oder entscheidende Informationen preiszugeben:
- Der Erwartungswert eines Glücksspiels kann entscheiden, ob dieses fair ist oder nicht, ohne weitere Details über dessen Regeln preiszugeben.
- Die Determinante eines linearen Gleichungssystems sagt aus, ob dieses eindeutig auflösbar ist oder nicht.
Auch elliptischen Kurven kann eine „Kennzahl“ zugeordnet werden. Man bezeichnet diese als Diskriminante. Für berechnet sich diese durch
Ist , so nennt man nicht-singulär. Der Fall korrespondiert zu singulären elliptischen Kurven. Letztere unterscheiden sich in der Theorie von den nicht-singulären, und werden im Rahmen der Vermutung von Birch und Swinnerton-Dyer nicht untersucht. Anschaulich bedeutet nicht-singulär, dass die Kurve „keine Knicke“ und „keine Schleifen“ hat.[5]
Gruppen[Bearbeiten | Quelltext bearbeiten]
Definition und Anschauung[Bearbeiten | Quelltext bearbeiten]


Gruppen wurden in der Mathematik eingeführt, um das Rechnen mit Zahlen zu verallgemeinern. Bei einer Gruppe handelt es sich um eine Menge von Objekten, zum Beispiel die ganzen Zahlen
und eine Verknüpfung auf dieser Menge, so dass gewisse Eigenschaften erfüllt sind. Mit Verknüpfung ist gemeint, dass man aus je zwei Elementen der Menge ein neues Element derselben erzeugen kann. Im Falle der ganzen Zahlen ist eine solche zum Beispiel die Addition: Die Summe zweier ganzer Zahlen ist wiederum eine ganze Zahl. Zusätzlich soll für eine Gruppe mit Verknüpfung gelten:
- Assoziativgesetz: Die Klammerung bei der Verknüpfung ist egal. Zum Beispiel gilt für alle . Es ist also unerheblich, welche Verknüpfung in einer Kette von solchen zuerst ausgeführt wird, solange die Reihenfolge der Elemente nicht verändert wird. Dies ist offenbar bei der Addition in den ganzen Zahlen erfüllt, etwa gilt .
- Existenz eines neutralen Elements: Es existiert ein Element , das bei Verknüpfung mit einem beliebigen anderen Element dieses unverändert lässt. Es gilt also für alle Elemente . In obigem Beispiel ist das neutrale Element die Null, denn es gilt und allgemein für jede (ganze) Zahl .
- Existenz des Inversen: Zu jedem Element gibt es ein Inverses, allgemein bezeichnet mit , sodass gilt, also unter Verknüpfung das neutrale Element herauskommt. In obigem Beispiel der ganzen Zahlen ist das Inverse zu , da stets gilt.
Es gibt unter den Gruppen auch solche, die mit Zusatzeigenschaften auffallen.
- Gilt zusätzlich zu den Gruppeneigenschaften noch das Kommutativgesetz, also für alle , so spricht man auch von einer abelschen Gruppe (zu Ehren von Niels Henrik Abel). Zum Beispiel ist eine abelsche Gruppe, da die Summe zweier Zahlen nach deren Vertauschung unverändert bleibt.
Es gibt zahlreiche weitere Beispiele für Gruppen, etwa die Menge der rationalen Zahlen ohne die Null, in Zeichen , mit der Multiplikation als Verknüpfung (das neutrale Element ist dann die ). Von Interesse sind jedoch auch endliche Gruppen. Ein alltägliches Beispiel ist das Rechnen mit Stunden und Uhrzeiten. Da man sich bei Tageszeiten nicht immer für das genaue Datum interessiert, beginnt der neue Tag nach „Stunde Null“ nicht (nur) mit „Stunde 24“, sondern wieder mit „Stunde Null“ (erkennbar beim Übergang von 23:59:59 zu 00:00:00 auf einer digitalen Uhr). Die Stundenanzeige weist also ein 24-periodisches Muster auf. Es ist dennoch möglich, in diesem Stundensystem in einer Addition zu rechnen. Ist das Datum nicht von Belang, ändert eine Addition von usw. Stunden nichts. Es ist in diesem Sinne zum Beispiel
Somit bildet das Kollektiv „aller vollen Stunden“ zusammen mit der eben erklärten „Addition“ eine endliche, abelsche Gruppe (mit als neutralem Element). In endlichen Gruppen ist es zwangsläufig so, dass die ständige Verknüpfung eines Elementes mit sich selbst irgendwann wieder beim neutralen Element mündet, im Falle der Stunden zum Beispiel
Man nennt die kleinste benötigte natürliche Anzahl der Verknüpfungen zur Erreichung des neutralen Elements auch die Ordnung des betroffenen Elements. Zum Beispiel ist in obigem Beispiel die Ordnung der gerade . Der Effekt des ständigen Verknüpfens eines Elements mit sich selbst bildet in endlichen Gruppen also einen „Kreislauf“, da ab dem neutralen Element wieder „von vorne“ begonnen wird. Zu beachten ist in diesem Kontext, dass analoge 24-Stunden-Uhren eine kreisförmige Form besitzen (siehe Bild). Zusätzlich kann bemerkt werden, dass sich dieses Beispiel an der Kuriosität von 24 Stunden orientiert, analoge Überlegungen aber für jede beliebige Zahl an Elementen funktionieren. Gruppen wie die obige mit allgemein Elementen bezeichnet man auch mit (im Falle der vollen Stunden also mit ).
Erzeuger von Gruppen[Bearbeiten | Quelltext bearbeiten]
Besonders „übersichtlich“ werden Gruppen, wenn man eine kleine Anzahl ihrer Elemente hinschreiben kann, die mit Hilfe der Verknüpfung jedes andere Element erzeugen können.
- Es ist ein Erzeuger der additiven Gruppe , denn durch
- werden alle positiven ganzen Zahlen durch sukzessive Addition erzeugt. Hierbei werden gleich zwei wichtige Prinzipen deutlich: Zu einem Erzeuger muss auch stets das inverse Element Beachtung finden (denn dieses ist eindeutig bestimmt, womit keine „wirklich neue“ Information hinzukommt), ergo ergänzen die Liste um die negativen ganzen Zahlen, und zweitens wird das neutrale Element stets trivial erzeugt, etwa durch . Man schreibt dann auch: .
- Es ist – nach dem selben Prinzip wie oben – ein Erzeuger der Gruppe . Allerdings ist zum Beispiel auch ein Erzeuger: Es kann jede Stundenzeit durch Zeitintervalle von je 5 Stunden generiert werden:
- und füllt man die Lücken, entsteht jede Uhrzeit genau einmal, bevor schließlich . Das zeigt, dass Erzeuger, selbst bis auf Invertierung, nicht eindeutig sind. Es gilt . Bei der Verwendung der Zeichen wird im Hintergrund stets in der Struktur der gerade untersuchten Gruppe gedacht.
Bei Weitem nicht alle Gruppen lassen sich durch ein einzelnes Element erzeugen. Gruppen, die das vermögen, nennt man zyklisch, und sind aus mathematischer Sicht besonders einfach. Die obigen Beispiele zeigen, dass und zyklisch sind.
Gruppenisomorphismen[Bearbeiten | Quelltext bearbeiten]
Um die „universelle Struktur“ hinter einer Gruppe, also quasi das detaillierte Netz des Zusammenspiels aller Elemente, zu erfassen, kann es hinderlich sein, sich zu sehr auf die gewählten Symbole für die Bezeichnung ihrer Elemente oder den Anwendungskontext zu fokussieren. Daher bezeichnet man zwei Gruppen und als isomorph, in Zeichen , falls es
- eine Eins-zu-Eins-Korrespondenz zwischen ihren Elementen gibt,
- und sich die Gruppengesetze beim „Wechsel in die andere Gruppe“ nicht ändern.
So könnte die obige Gruppe auch als bezeichnet werden (mit , , usw.), und gemäß des Isomorphismus würde sich zum Beispiel die Rechnung
- in
übersetzen. Dies verdeutlicht erneut die Nützlichkeit von Isomorphismen: Die Untersuchung einer Struktur hängt nicht von kulturellen Aspekten, etwa der Benennung von Zahlen mit arabischen Symbolen, oder dem Untersuchungskontext, ab - es kommt nur auf das exakte Zusammenspiel ihrer Elemente an, egal wie sie „heißen“. Ferner wird damit ein „Brückenbau“ zwischen Theorien ermöglicht: Wie gesehen, hat die abstrakte endliche Gruppe Anwendungen auf die menschengewählten Stundenzeiten – taucht aber auch in der Zahlentheorie im Kontext der Zahl 24 auf.
Es kann auch passieren, dass zwei Gruppen mit scheinbar „unterschiedlichen“ Verknüpfungen isomorph sind, also letztlich über exakt die gleiche Struktur verfügen. Ein Beispiel ist der „2-Stunden-Tag“ mit und die multiplikative Gruppe , denn es gilt ebenso ; es liefert dann die Abbildung mit den Isomorphismus.
Hauptsatz über endlich erzeugte abelsche Gruppen[Bearbeiten | Quelltext bearbeiten]
Der zentrale Aspekt der Gruppenisomorphie macht es in der Gruppentheorie besonders einfach, mit „allen Gruppen“ zu arbeiten, da die Identifikation mittels Isomorphismen eine bequeme Form der Abstraktion ermöglicht. Ein, auch für die Vermutung von Birch und Swinnerton-Dyer, sehr wichtiges Beispiel ist die Klassifikation aller endlich erzeugten abelschen Gruppen. Dazu ist zunächst eine einfache Beobachtung wichtig: Man kann aus zwei Gruppen und eine neue Gruppe „bauen“, indem man für und mit den Tupeln rechnet. Sind und additive Gruppen, definiert man folgende komponentenweise Verknüpfung auf
Auf diese Weise wird zu einer Gruppe, und es gilt . Es gibt keine Limitierung für diese sog. direkten Produkte, und so bilden auch usw. Gruppen mit entsprechend vielen „Komponenten“. Es wird zudem abkürzend
geschrieben (in dieser Notation ist die triviale Gruppe). Ist nun eine endlich erzeugte abelsche Gruppe, so kann gezeigt werden, dass es stets Zahlen sowie gibt mit einem Isomorphismus der Form
Stellt man gewisse Forderungen an die , so können diese in Termen von eindeutig bestimmt werden. Es wird der endliche Teil auch als Torsionsteil bezeichnet; er beinhaltet alle Elemente, die sich mit ständiger Verknüpfung mit sich selbst irgendwann zu Null addieren, also den oben beschriebenen Kreislauf bilden. Der (im Fall ) unendliche Teil der Gruppe ist im Kontext der Vermutung von Birch und Swinnerton-Dyer von besonders großem Interesse.
Das Gruppengesetz auf elliptischen Kurven und der Satz von Mordell-Weil[Bearbeiten | Quelltext bearbeiten]
Einführung und Motivation durch Gerade und Kreis[Bearbeiten | Quelltext bearbeiten]


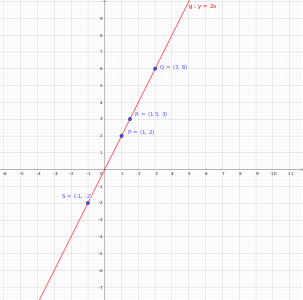
Auf den rationalen Punkten einiger algebraischer Kurven kann ein Gruppengesetz erklärt werden. Ein Beispiel ist die Gerade mit Steigung . Diese ist gegeben durch die Ansammlung aller Punkte der Form . Zum Beispiel liegen die Punkte
auf dieser Geraden. Wegen der Proportionalität beider Komponenten – sie unterscheiden sich bloß um den Faktor – können Punkte auf der Geraden komponentenweise zu neuen Punkten addiert werden. Etwa liegt
erneut auf der Geraden. Dies funktioniert auch für nichtganze Punkte, da aber die rationalen Zahlen unter Addition selbst abgeschlossen sind (auch bildet eine abelsche Gruppe), formen alle rationalen Punkte auf der Geraden mit Steigung eine abelsche Gruppe mit neutralem Element . Durch die 1:1-Korrespondenz ist diese Gruppe sogar isomorph zu .
Auch für den Kreis ist die Angabe eines Gruppengesetzes möglich (siehe auch Gruppe der rationalen Punkte auf dem Einheitskreis). Liegen die rationalen Punkte und auf dem Einheitskreis, so auch der rationale Punkt
- .
Das Symbol für die Gruppenverknüpfung deutet an, dass es sich nicht mehr um eine „gewöhnliche Addition“ handelt. Mit dieser Verknüpfung können aus bekannten rationalen Punkten auf dem Einheitskreis neue gewonnen werden; so gilt
wobei für die verknüpften Punkte und zu beachten ist. In der Tat gilt auch . Es kann dieses Gesetz zwar direkt nachgerechnet werden, allerdings rührt es auf natürliche Weise aus der Parametrisierung des Kreises durch Sinus und Kosinus (siehe Bild) und den Additionstheoremen der Winkelfunktionen her:
Das Gruppengesetz ergibt sich daraus unmittelbar durch und , und das Ergebnis kann geometrisch als der Punkt gedeutet werden, der sich nach Addition der Winkel der Ursprungspunkte ergibt. In der Winkelparametrisierung vereinfacht sich das Gruppengesetz also auf die Vorschrift
Die genaue Struktur der Gruppe der rationalen Punkte auf dem Einheitskreis ist komplizierter als jene auf einer Geraden, kann aber auf mathematisch zufriedenstellende Art beschrieben werden.
Das Gruppengesetz auf elliptischen Kurven[Bearbeiten | Quelltext bearbeiten]
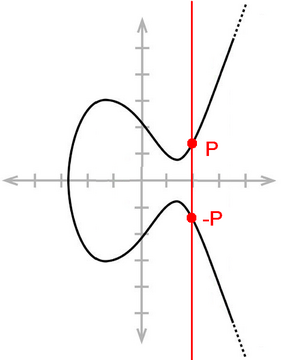
Auch auf elliptischen Kurven über den rationalen Zahlen kann ein Gruppengesetz auf den rationalen Punkten definiert werden. Dieses lässt sich am besten geometrisch erklären. Werden zwei Punkte auf der Kurve verknüpft, wird zur Bestimmung des neuen Punktes die Gerade durch beide addierten Punkte gelegt, und der dritte Schnittpunkt mit der elliptischen Kurve an der x-Achse gespiegelt (siehe Bild). Das neutrale Element dieser Verknüpfung ist ein „Punkt“, der „unendlich weit entfernt“ liegt, und formal zur Kurve hinzugefügt wird. Dies bedeutet insbesondere, dass das Inverse eines Punktes stets die Spiegelung des Ursprungspunktes an der x-Achse ist. Der Beweis, dass die Kollektion aller rationalen Punkte inklusive tatsächlich eine Gruppe bildet, ist wegen des notwendigen Nachweises des Assoziativgesetzes mühsam.
-
Geometrische Interpretation der Addition auf einer elliptischen Kurve und Spiegelung am „unendlich entfernten Punkt“
-
Schaubild der Punktaddition mit und auf der elliptischen Kurve
-
Bei der Verdopplung muss die Tangente der Kurve an gelegt werden
-
Das Inverse eines (rationalen) Punktes ist stets die Spiegelung an der x-Achse, denn der „dritte Schnittpunkt“ ist unendlich weit weg
Das Phänomen des „unendlich fernen Punktes“ wird mathematisch mittels der projektiven Geometrie rigoros beschrieben. Erster Schritt ist dabei die Homogenisierung der Kurve unter Hinzufügung einer dritten Variable , also , sodass alle Monome den gleichen Grad 3 haben.
Zwar lässt sich die Punktaddition auf einer elliptischen Kurve geometrisch anschaulich erklären, fußt aber – ähnlich wie beim Einheitskreis – auf der rechnerischen Seite vollends auf den vier Grundrechenarten. Eine geschlossene Formel ist jedoch mühsam hinzuschreiben. Dies ist von großer Wichtigkeit, weil es von Vorteil ist, elliptische Kurven auch über anderen Körpern als nur den reellen oder rationalen Zahlen zu studieren. Dazu gehören auch Körper, in denen eine oben angeführte geometrische Sichtweise gar nicht mehr möglich ist.
Der Satz von Mordell-Weil[Bearbeiten | Quelltext bearbeiten]
Bis heute existiert kein Verfahren, zu entscheiden, ob eine beliebige elliptische Kurve über den rationalen Zahlen einen rationalen Punkt hat (der „unendlich ferne Punkt“ wird nicht dazugezählt). Allerdings weiß man, dass es stets „deutlich weniger“ rationale Punkte als im Falle etwa der Geraden oder des Einheitskreises sind, sofern die Kurve nicht-singulär ist. Der Satz von Mordell-Weil besagt, dass die abelsche Gruppe der rationalen Punkte auf einer elliptischen Kurve endlich erzeugt ist. Es gibt also stets eine endliche Anzahl von fest gewählten Punkten , so dass sich jeder Punkt in der Form
- (dabei ist für definiert: bzw. )
mit irgendwelchen schreiben lässt. Die Anzahl der benötigten Erzeuger kann selbstverständlich mit der Wahl der Kurve variieren. Nach der Klassifikation endlich erzeugter abelscher Gruppen gibt es also ein , so dass
wobei der Torsionsteil ist, also alle Punkte, die sich bei ständiger Addition mit sich selbst „im Kreis bewegen“. Die Zahl ist durch die Kurve fest bestimmt, also eine ihr zugehörige Größe, und heißt der algebraische Rang von . Sie misst ab, „wie viele“ rationale Punkte auf liegen. Etwa sind es im Fall stets nur endlich viele, und ab Rang unendlich viele, aber das „Maß der Unendlichkeit“ nimmt mit steigendem algebraischem Rang zu. Die Vermutung von Birch und Swinnerton-Dyer macht eine Aussage über den algebraischen Rang einer elliptischen Kurve über den rationalen Zahlen.
Elliptische Kurven über endlichen Körpern[Bearbeiten | Quelltext bearbeiten]
In der Mathematik bezeichnet ein Körper eine Menge, innerhalb der, einfach gesprochen, mit den vier Grundrechenarten gerechnet werden kann. Dabei sollen die aus der Schulmathematik bekannten Regeln des Kommutativgesetzes (Vertauschbarkeit bei „Plus“ und „Mal“), Assoziativgesetzes (Vertauschbarkeit von Klammern bei „nur Plus“ oder „nur Mal“) und Distributivgesetzes („Ausklammern“ und „Ausmultiplizieren“) gelten. Außerdem muss stets das Element (neutrales Element der Addition) und (neutrales Element der Multiplikation) Teil eines Körpers sein. Insbesondere soll durch jede Zahl ungleich der dividiert werden können. Wichtige Beispiele sind der Körper der reellen Zahlen (Bezeichnung: ) oder der Körper der rationalen Zahlen (Bezeichnung: ).
In exakter mathematischer Fachsprache ist genau dann ein Körper, wenn bzw. eine additive bzw. multiplikative abelsche Gruppe formen, und gleichzeitig das Distributivgesetz (als „Verträglichkeit“ zwischen Plus und Mal) gilt.
Neben den etwa aus der Schulmathematik bekannten Körpern der rationalen und reellen Zahlen existieren viele weitere Beispiele, darunter sogar auch endliche Körper. Die einfachsten endlichen Körper entstehen nach Wahl einer beliebigen Primzahl . Wie bereits gesehen, bildet dann eine additive abelsche Gruppe. Die Primzahleigenschaft ermöglicht aber auch eine Multiplikation und Division (durch Zahlen ungleich ) innerhalb . Ist zum Beispiel , so ist das multiplikative Inverse von , denn
Elliptische Kurven können auch über den Körpern betrachtet werden. Dort existiert weiterhin eine Punktaddition, da diese lediglich die vier Grundrechenarten benötigt. Auch ist es möglich (und notwendig), einen „unendlich fernen“ Punkt zu betrachten. Für die Vermutung von Birch und Swinnerton-Dyer ist es nun essentiell, die Anzahl der Punkte für jeden der Körper usw. zu betrachten (es werden stets endlich viele sein).
Beispiel: Es hat die elliptische Kurve genau fünf Punkte über dem Körper , nämlich und . Zum Beispiel gilt in
wegen Division durch mit Rest. Also ist in diesem Fall .
Auch wenn es schwierig ist, für sehr große Primzahlen die genaue Anzahl zu berechnen, existiert ein wichtiger Satz von Helmut Hasse, der eine recht präzise Vorstellung davon gibt, wie groß die Lösungszahl ist (den unendlich fernen Punkt ausgenommen). Für diese gilt[6]
Für sehr große Primzahlen bedeutet dies, dass die Anzahl der Punkte im Verhältnis sehr nah an liegt, also .
Aussage der Vermutung[Bearbeiten | Quelltext bearbeiten]

In ihrer einfachsten Form sagt die Vermutung von Birch und Swinnerton-Dyer aus, dass sich der algebraische Rang einer elliptischen Kurve – ein globales Datum – aus ihren lokalen Eigenschaften – also den Punktanzahlen der reduzierten Kurven über den endlichen Körpern – ermitteln lässt.
Vermutung: Sei eine nicht-singuläre elliptische Kurve über den rationalen Zahlen mit algebraischem Rang . Es bezeichne die Anzahl der Punkte auf der reduzierten Kurve . Dann gibt es eine Konstante , sodass .[7]
Dabei bedeutet das Symbol , dass beide Seiten für wachsende Werte gleich schnell anwachsen.
Hintergrund und Interpretation[Bearbeiten | Quelltext bearbeiten]
In vielen Wissenschaften ist es essenziell, Systeme, also grob gesprochen das globale Zusammenspiel vieler verschiedener Elemente, zu verstehen und Prognosen machen zu können. Da Systeme nach Ausmaß sehr komplex sein können, kann es helfen, zuerst „lokale“ Aspekte eines Systems zu studieren, um diese „lokalen Faktoren“ gegebenenfalls zu einem „globalen Verständnis“ verheften zu können. Aus offensichtlichen Gründen ist das Studium lokaler Aspekte leichter als jenes des ganzen Systems, da ein Verständnis des letzteren auch Aufschluss über Einzelfragen geben könnte. Zum Beispiel kann versucht werden, aus den Eigenschaften des „Durchschnittsmenschen“ auf die Dynamik innerhalb einer Staatengemeinschaft rückzuschließen. Ein weiteres Beispiel ist die Beschreibung globaler ökonomischer Zusammenhängen durch Modelle in der Makroökonomie (etwa das AS-AD-Modell mit Fokussierung auf die „lokalen“ Parameter Gesamtangebot und Gesamtnachfrage).
Auch in der Zahlentheorie hat eine Form des „Lokal-Global-Prinzips“ Methode. Das zu untersuchende „System“ kann dabei zum Beispiel eine Gleichung sein, wie etwa über den rationalen Zahlen, und die Frage „an das System“, ob diese über den rationalen Zahlen lösbar ist. Dazu ist zunächst zu klären, welche „lokalen Faktoren“ die Zahlen aufbauen: Nach dem Fundamentalsatz der Arithmetik ist bekannt, dass sich jede ganze Zahl bis auf Vorzeichen und Faktorreihenfolge eindeutig in Primfaktoren zerlegen lässt. Zum Beispiel gilt
Lässt man auch negative Exponenten zu, überträgt sich dieses Prinzip sogar auf rationale Zahlen :
Durch die Systematisierung der algebraischen Zahlentheorie seit dem 19. Jahrhundert ist bekannt, dass das „Zusammenspiel“ der „lokalen Faktoren“, also der „Primstellen“, ein globales Verständnis der Zahlen liefern kann. Konkret bedeutet dies, dass es in manchen Fällen hilft, eine Gleichung bzw. Kurve zuerst an den „lokalen Stellen“, also über den einfacher zu handhabenen Körpern sowie zu studieren, um ggf. Aufschluss über „globale“, also rationale Lösungen, zu erhalten.
Das Lokal-Global-Prinzip scheitert, wenn die algebraische Kurve „zu kompliziert“ wird. In diesem Fall müssen weitere Informationen beschafft werden, um doch noch entscheiden zu können, ob ein nicht-trivialer rationaler Punkt existiert. Der Mathematiker Ernst Sejersted Selmer zeigte zum Beispiel, dass die Gleichung bezüglich jeder Primzahl in obigem Sinne eine Lösung besitzt, und ebenfalls eine reelle Lösung, aber keine nicht-triviale (also ) rationale Lösung.
Die Vermutung von Birch und Swinnerton-Dyer ist eine Variante des Lokal-Global-Prinzips für elliptische Kurven über den rationalen Zahlen. Dabei geht sie über den bloßen Versuch, irgendeinen rationalen Punkt vorherzusagen, hinaus. Insbesondere soll der algebraische Rang der Kurve aus ihren lokalen Daten ermittelt werden. Präziser sagt die Vermutung einen Zusammenhang zwischen der Kurve an Primstellen und ihrem algebraischen Rang voraus. Um dabei dem Scheitern des Lokal-Global-Prinzips für elliptische Kurven etwas entgegenzusetzen, werden die Anforderungen an die Informationen an den Primstellen verschärft. Es wird nicht nur nach der Existenz einer Lösung modulo gefragt, sondern nach der genauen Anzahl.
Formulierung über L-Funktionen[Bearbeiten | Quelltext bearbeiten]
Die L-Funktion einer elliptischen Kurve[Bearbeiten | Quelltext bearbeiten]
Unter enormen Anstrengungen konnte im Rahmen des Modularitätssatzes Ende des 20. Jahrhunderts gezeigt werden, dass man elliptischen Kurven eine mathematische Funktion zuordnen kann, nämlich ihre sog. L-Funktion, die auf den reellen (ja sogar komplexen Zahlen) definiert ist und dort „sehr gute analytische Eigenschaften“ wie Differenzierbarkeit besitzt. Die Vermutung von Birch und Swinnerton-Dyer besagt nun, dass diese L-Funktion die Anzahl der rationalen Punkte auf der elliptischen Kurve „kennt“: Sie wird durch die Ordnung der Nullstelle an der Stelle kodiert. Dabei bedeutet Ordnung die „Häufigkeit des Faktors im Funktionsterm“; in diesem Sinne hat die Funktion in eine Nullstelle der Ordnung 4. Je höher die Ordnung ist, so die Vermutung, „desto mehr“ rationale Punkte liegen auf der elliptischen Kurve.
Für ein umfassendes Verständnis der L-Funktion einer elliptischen Kurve sind komplexe Zahlen vonnöten. Jedoch sind deren Motivation und Konstruktion sowie die Formulierung der Vermutung von Birch und Swinnerton-Dyer auch mittels der aus der Schulmathematik bekannten reellen Zahlen möglich.
Der analytische Rang[Bearbeiten | Quelltext bearbeiten]
Jeder nicht-singulären elliptischen Kurve über mit Level kann eine L-Funktion zugeordnet werden, die als analytisches Objekt alle arithmetischen Eigenschaften kodiert. Diese besitzt eine Darstellung als Euler-Produkt:
wobei die für Primzahlen mit good reduction gegeben sind durch und die Menge der Lösungen modulo bezeichnet. Für Primzahlen mit bad reduction wird eine ähnliche Definition gewählt.[8] Falls die Koeffizienten der Kurve keine ganzen Zahlen sind, muss dafür zunächst eine elementare Umformung über projektive Koordinaten vorgenommen werden.[9] L-Funktionen können auch für den Fall elliptischer Kurven über beliebigen Zahlkörpern definiert werden.[10] Andrew Wiles und anderen gelang mit dem Beweis des Modularitätssatzes die Bestätigung der Aussage, dass zu einer ganzen Funktion fortgesetzt werden kann und einer Funktionalgleichung genügt: Tatsächlich korrespondiert mit einer Modulform von Gewicht 2, deren Level mit dem Führer der elliptischen Kurve identisch ist. Insbesondere ist eine sog. Hecke-Eigenform bezüglich der Kongruenzuntergruppe . Formelhaft ergibt sich der Zusammenhang zwischen und via klassischer Mellin-Transformation:
Die Funktionalgleichung lautet dann
wobei das Vorzeichen eine wichtige Rolle für die Arithmetik von spielt. Beispielsweise verschwindet mit gerader/ungerader Ordnung in , falls den Wert bzw. annimmt.[11]
Geschichte[Bearbeiten | Quelltext bearbeiten]
Diophantos und Fermat[Bearbeiten | Quelltext bearbeiten]
Probleme im Kontext von elliptischen Kurven, also solchen mit Geschlecht 1, spielen eine bedeutende Rolle innerhalb von Diophantos von Alexandrias Werk Arithmetica. Schneidet eine reelle Gerade eine elliptische Kurve an zwei Punkten oder als Tangente in einem Punkt „doppelt“, so hat sie auch einen dritten reellen Schnittpunkt. Wenn nun zwei dieser Schnittpunkte rationale Punkte sind, so ist es auch der dritte. Diese Tatsache wurde schon von Isaac Newton festgestellt. Besonders bemerkenswert ist, dass das Zeichnen einer Tangente an einem rationalen Punkt der Kurve dazu führt, dass diese Tangente die Kurve erneut an einem rationalen Punkt schneidet. Diophantos wandte diese Methode implizit an, um von einer ersten Lösung auf eine zweite zu gelangen. Jedoch iterierte er diesen Prozess nicht. Es war Pierre de Fermat, der als Erster erkannte, dass auf diese Weise gelegentlich unendlich viele Lösungen erzielt werden können. Ferner führte Fermat eine „Methode des Abstiegs“ ein, die gelegentlich dazu verwendet werden kann, zu zeigen, dass die Anzahl der Lösungen endlich oder sogar null ist.
Im 21. Jahrhundert: Erklärung zum Millennium-Problem[Bearbeiten | Quelltext bearbeiten]

Bereits im Jahr 1998 wurde das Clay Mathematics Institute (CMI) durch den Geschäftsmann Landon T. Clay und den Mathematiker Arthur Jaffe gegründet,[12] wobei Jaffe von 1998 bis 2011 auch die erste Präsidentschaft innehatte. Das CMI feierte das einhundertste Jahr nach Hilberts Rede auf dem Pariser Kongress im Jahr 1900 durch eine zweitägige Konferenz am Collège de France im Mai 2000. Dabei wurde ein 7-Millionen-Dollar-Fonds vorgestellt, von dem jeweils 1 Million Dollar für die Lösung von sieben großen mathematischen Problemen vergeben wird, den sogenannten Millennium-Problemen.[13] Die Preise wurden schließlich im Juni bekanntgegeben, nach Angaben des CMI ins Leben gerufen, um
- einige der wohl schwierigsten Probleme zu würdigen, mit denen Mathematiker um die Jahrtausendwende zu kämpfen hatten,
- die Bedeutung der Arbeit an den wirklich schwierigen Problemen zu unterstreichen und
- bekannter zu machen, dass es in der Mathematik immer noch schwierige, bedeutende Probleme gibt.[14]
Da im 20. Jahrhundert kein Beweis für die Vermutung von Birch und Swinnteron-Dyer gefunden wurde, ist dieses Vorhaben zu einem der Millennium-Probleme erklärt worden.
Damit das Preisgeld verliehen werden kann, muss die betroffene Arbeit publiziert worden sein, und nach einer Ruhefrist von 2 Jahren von der Mathematikergemeinschaft eine breite Akzeptanz erfahren haben.[15] Unter den Regeln der Preisverleihung findet sich ferner auch eine Klausel bezüglich der Rolle von Gegenbeispielen. Im Falle der Vermutung von Birch und Swinnerton-Dyer wäre ein Gegenbeispiel eine (nicht-singuläre) elliptische Kurve über den rationalen Zahlen, für die
gilt. Dieses könnte sich durch individuelle Untersuchung einer (einzigen) Kurve auffinden lassen. Falls nach Ansicht des CMI das Gegenbeispiel das Problem tatsächlich löst, könne das CMI die Verleihung des Hauptpreises aussprechen. Zeige hingegen das Gegenbeispiel, dass das ursprüngliche Problem nach Umformulierung oder Eliminierung eines Spezialfalls weiterbesteht, könne das CMI dem Autor lediglich einen kleinen Preis verleihen, dessen Höhe CMI nach eigenem Ermessen festlegt. Das Geld für diesen Preis werde dann nicht aus dem Problemfonds, sondern aus anderen CMI-Fonds entnommen.[16]
Bedeutung[Bearbeiten | Quelltext bearbeiten]
Kongruente Zahlen[Bearbeiten | Quelltext bearbeiten]
Eine kongruente Zahl ist eine rationale Zahl , die der Flächeninhalt eines rechtwinkligen Dreiecks mit ausschließlich rationalen Seitenlängen ist. Es existiert stets eine Zahl , so dass eine quadratfreie ganze Zahl ist (also eine Zahl, die von keiner Quadratzahl außer 1 geteilt wird). Jedoch hat das entsprechende Dreieck mit Seitenlängen den Flächeninhalt , weshalb ohne Beschränkung der Allgemeinheit als quadratfreie ganze Zahl gewählt werden kann. Es bleibt dennoch zu beachten, dass nicht gefordert wird, dass die Seitenlängen des Dreiecks selbst ganze Zahlen sind. Während die kleinste kongruente Zahl ist, bei der dies realisiert werden kann (siehe Bild), ist auch eine kongruente Zahl mit Seitenlängen
Zwar existiert ein Algorithmus zur Berechnung theoretisch aller kongruenter Zahlen, jedoch ist nicht bekannt, wie lange dieses Verfahren benötigt, etwa zu entscheiden, ob eine bestimmte Zahl kongruent ist.[17] Es kann jedoch auf „elementare Weise“ gezeigt werden, dass genau dann kongruent ist, falls die zugehörige elliptische Kurve
unendlich viele rationale Punkte hat. Durch tiefe Resultate von John Coates und Andrew Wiles ist bekannt, dass, falls tatsächlich unendlich viele rationale Punkte hat, notwendigerweise gelten muss. Ist also umgekehrt , so kann nicht kongruent sein. Die Vermutung von Birch und Swinnerton-Dyer liefert die andere Richtung: Ist , so hat unendlich viele rationale Punkte, und ist eine kongruente Zahl.[18]
Jerrold Tunnell konnte zudem folgenden Satz finden, der eine elementare „Charakterisierung“ kongruenter Zahlen leistet: Ist quadratfrei und eine kongruente Zahl, so gelten
Falls die Vermutung von Birch und Swinnerton-Dyer auf die elliptischen Kurven zutrifft, so gilt auch die umgekehrte Richtung, also aus den obigen Gleichheiten zwischen Mächtigkeiten von Mengen folgt die Kongruenz von . Benedict Gross und Don Zagier konnten im Jahr 1983 zeigen, dass eine große Familie innerhalb der die Vermutung von Birch und Swinnerton-Dyer tatsächlich erfüllt.[19]
Rationale Punkte auf Kurven mit Geschlecht 1[Bearbeiten | Quelltext bearbeiten]

Was elliptische Kurven über den rationalen Zahlen so in den Fokus des Interesses rückt, ist die Tatsache, dass sie die einzigen Kurven sind, die nur endlich viele, aber auch unendlich viele rationale Punkte haben können.
Elliptische Kurven haben nun das Geschlecht und nach der Vermutung von Mordell, bewiesen von Gerd Faltings, haben Kurven von Geschlecht (dazu gehören lineare und quadratische Kurven) mit einem rationalen Punkt bereits unendlich viele rationale Punkte, während Kurven von Geschlecht stets nur endlich viele rationale Punkte haben können.[20] Ein entscheidendes Werkzeug in Faltings Beweis war die nach ihm benannte Faltings-Höhe, eine sehr weitreichende Verallgemeinerung des von Pierre de Fermat eingeführten Prinzips des unendlichen Abstiegs: In manchen Fällen kann man aus einer potenziellen Lösung eine unendliche Kette neuer Lösungen konstruieren, die dann aber zu einer ebenfalls unendlichen Kette absteigender natürlicher Zahlen korrespondiert, was absurd ist: Etwa lässt sich der absteigende Prozess
nicht mit unendlich vielen natürlichen Zahlen füllen. Zum Beispiel besagt der Satz von Faltings, dass die Kurve
von Geschlecht nur endlich viele rationale Punkte besitzt, darunter die trivialen Lösungen und . Durch den Beweis des Großen Fermatschen Satzes konnten weitere rationale Lösungen darüber hinaus ausgeschlossen werden. Für seine Leistung wurde Faltings 1986 als damals erster Deutscher mit der Fields-Medaille, dem „Nobelpreis der Mathematik“, geehrt.[21]
Heuristik[Bearbeiten | Quelltext bearbeiten]
Der Mathematiker Neal Koblitz hat auf ein heuristisches Argument hingewiesen, das auf die Richtigkeit einer schwachen Form der Vermutung von Birch und Swinnerton-Dyer hinweist, aber seiner Aussage nach „weit“ von einem rigorosen Beweis entfernt ist. Nimmt man an, dass das Euler-Produkt zu in die Funktion darstellt (was nicht der Fall ist!), hätte man
wobei die Anzahl der -Punkte auf bezeichnet. Wenn die Primzahlen variieren, „überspannen“ die Werte den Wert innerhalb einer maximalen Intervalllänge , wie es der Satz von Hasse besagt. Also gilt grob gesagt . Hätte dies ein „oszillierendes Muster“, also eine etwa gleich häufige Anzahl von Schwankungen in die eine und die andere Richtung, könnte man auf die „Konvergenz“ des Produktes gegen einen Grenzwert schließen. Hätte jedoch die Tendenz, auf der „größeren Seite“ zu sein, würde man
erhalten. Das heuristische Argument ergibt sich nun daraus, dass, falls unendlich viele rationale Punkte hat, zu erwarten wäre, dass deren Reduktion modulo stets zu einer eher größeren Zahl führen sollte. Hätte hingegen nur endliche viele rationale Punkte, so wäre deren Beitrag zu vernachlässigbar, sodass ein eher „zufälliges“, also schwankendes, Verhalten die Konsequenz wäre.[22]
Numerische Evidenz[Bearbeiten | Quelltext bearbeiten]
Es existiert starke numerische Evidenz für die Vermutung.

Forschungsgeschichte[Bearbeiten | Quelltext bearbeiten]
Die Vermutung wurde bisher nur in Spezialfällen bewiesen:
- 1976 bewiesen John Coates und Andrew Wiles, dass, wenn eine elliptische Kurve mit „komplexer Multiplikation“ ist und nicht 0 ist, nur eine endliche Zahl rationaler Punkte hat. Sie bewiesen dies für imaginär quadratische Körper – aus diesen kommt der Faktor bei der „komplexen Multiplikation“ − mit der Klassenzahl 1, von Nicole Arthaud (Arthaud-Kuhman) wurde dies auf alle imaginärquadratischen Zahlkörper erweitert.
- 1983 zeigten Benedict Gross und Don Zagier, dass, wenn eine modulare elliptische Kurve[23] eine Nullstelle erster Ordnung bei hat, es einen rationalen Punkt unendlicher Ordnung gibt.
- 1990 zeigte Victor Kolyvagin, dass für eine modulare elliptische Kurve, für die eine Nullstelle 1. Ordnung bei hat, der Rang ist. Außerdem zeigte er ebenfalls für modulare Kurven, dass ist, falls dort keine Nullstelle hat.
- 1991 zeigte Karl Rubin, dass für elliptische Kurven mit komplexer Multiplikation mit Elementen aus einem imaginär-quadratischen Zahlkörper sowie mit nicht verschwindender L-Reihe bei , der „-Anteil“ der Tate-Shafarevich-Gruppe die aus der Birch-Swinnerton-Dyer-Vermutung folgende Ordnung hat, für alle Primzahlen .
- 1999 zeigten Andrew Wiles, Christophe Breuil, Brian Conrad, Fred Diamond und Richard Taylor, dass alle elliptischen Kurven über den rationalen Zahlen modular sind (Taniyama-Shimura-Vermutung),[24] so dass die Ergebnisse von Kolyvagin und Rubin für alle elliptischen Kurven über den rationalen Zahlen gelten.
- Jan Nekovář zeigte um 2000 in einer kohomologischen Version der Vermutung über Selmer-Gruppen und -Komplexe um 2002, dass die Vermutung „modulo 2“ (Parität 2) richtig ist und es gibt eine Vermutung zu höheren Paritäten. Nekovář verallgemeinerte auch die BSD-Vermutung auf höhere Ordnungen der Nullstelle als 1 (Plektische Vermutung).[25]
- 2010 zeigte Manjul Bhargava mit Arul Shankar, dass ein positives Maß der elliptischen Kurven über den rationalen Zahlen Rang 0 hat und die Vermutung von Birch und Swinnerton-Dyer erfüllt.[26] 2014 zeigten Bhargava, Christopher Skinner und Wei Zhang, dass dies für die Mehrheit (über 66 Prozent) elliptischer Kurven zutrifft.[27]
Für Kurven mit Gruppen, die einen Rang haben, wurde bisher nichts bewiesen, es gibt aber starke numerische Argumente für die Korrektheit der Vermutung.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Avner Ash, Robert Gross: Elliptic Tales. Curves, Counting, and Number Theory. Princeton University Press, 2012, ISBN 0691151199.
- Bryan Birch, Peter Swinnerton-Dyer: Notes on elliptic curves. II. J. Reine Angew. Math. 218 (1965), 79–108.
- John Coates: The Conjecture of Birch and Swinnerton-Dyer. In: John Forbes Nash Jr., Michael Th. Rassias (Hrsg.): Open problems in mathematics. Springer 2016, ISBN 978-3-319-32160-8 (englisch), S. 207–224.
- Henri Cohen: Number Theory, Volume I: Tools and Diophantine Equations (= Graduate texts in mathematics. Band 239). Springer, New York 2007, ISBN 978-0-387-49922-2 (englisch).
- Dale Husemöller: Elliptic curves. With appendices by Otto Forster, Ruth Lawrence, and Stefan Theisen (= Graduate texts in mathematics. Band 111). 2. Auflage. Springer, New York 2004, ISBN 0-387-95490-2 (englisch, 487 S.).
- Kenneth Ireland, Michael Rosen: A Classical Introduction to Modern Number Theory (= Graduate texts in mathematics. Band 84). 2. Auflage. Springer Verlag, New York 1990, ISBN 0-387-97329-X (englisch).
- Anthony W. Knapp: Elliptic curves (= Mathematical notes. Band 40). Princeton University Press, Princeton, N.J. 1992, ISBN 0-691-08559-5 (englisch).
- Neal Koblitz: Introduction to elliptic curves and modular forms (= Graduate texts in mathematics). Springer, New York 1984, ISBN 0-387-96029-5 (englisch).
- Jürg Kramer: Die Vermutung von Birch und Swinnerton-Dyer. In: Elemente der Mathematik. Band 57, 2002, S. 115–120.
- Serge Lang: Faszination Mathematik. Ein Wissenschaftler stellt sich der Öffentlichkeit. Vieweg, Braunschweig/Wiesbaden 1989, ISBN 3-528-08956-3, doi:10.1007/978-3-322-85603-6 (135 S., Übersetzung von Günther Eisenreich).
- Serge Lang: Elliptic curves – diophantine analysis (= Grundlehren der mathematischen Wissenschaften. Band 231). Springer, Berlin / New York 1978, ISBN 0-387-08489-4 (englisch, 261 S.).
- Peter Meier, Jörn Steuding, Rasa Steuding: Elliptische Kurven und eine kühne Vermutung. In: Spektrum der Wissenschaft. Dossier: „Die größten Rätsel der Mathematik“ (6/2009), ISBN 978-3-941205-34-5, Seite 40–47.
- Karl Rubin, Alice Silverberg: Ranks of elliptic curves. In: Bulletin of the American Mathematical Society. Band 39, 2002, ISSN 1088-9485, S. 455–474, doi:10.1090/S0273-0979-02-00952-7 (englisch, Download des vollständigen Artikels [PDF; 537 kB; abgerufen am 26. Dezember 2020]).
- Joseph H. Silverman: The Arithmetic of Elliptic Curves (= Graduate texts in mathematics. Band 106). 2. Auflage. Springer, Dordrecht / Heidelberg / London / New York 2009, ISBN 978-0-387-09493-9 (englisch).
- Joseph H. Silverman: Advanced Topics in the Arithmetic of Elliptic Curves (= Graduate texts in mathematics. Band 151). Springer, New York 1994, ISBN 978-0-387-94328-2 (englisch).
- Joseph H. Silverman, John Tate: Rational points on elliptic curves. Springer, New York 1992, ISBN 0-387-97825-9 (englisch).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Andrew Wiles: The Birch and Swinnerton-Dyer conjecture. (PDF; 140 kB). Offizielle Problembeschreibung im Rahmen der Millennium-Probleme.
- Jürg Kramer: Die Vermutung von Birch und Swinnerton-Dyer.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Elliptic curve with LMFDB label 20.a3, The L-functions and modular forms database (LMFDB), Abgerufen am 26. Dezember 2023.
- ↑ Elliptic curve with LMFDB label 37.a1, The L-functions and modular forms database (LMFDB), Abgerufen am 26. Dezember 2023.
- ↑ Elliptic curve with LMFDB label 664.a1, The L-functions and modular forms database (LMFDB), Abgerufen am 26. Dezember 2023.
- ↑ Elliptic curve with LMFDB label 27584.a1, The L-functions and modular forms database (LMFDB), Abgerufen am 26. Dezember 2023.
- ↑ Joseph H. Silverman: The arithmetic of elliptic curves. 2. Auflage. Dordrecht / Heidelberg / London / New York, 2009, S. 42–45.
- ↑ Anthony W. Knapp: Elliptic curves, Princeton, N.J., 1992, S. 296.
- ↑ Anthony W. Knapp: Elliptic curves, Princeton, N.J., 1992, S. 17.
- ↑ Gary Cornell, Joseph H. Silverman, Glenn Stevens (Hrsg.): Modular Forms and Fermat’s Last Theorem. Springer, S. 97.
- ↑ Joseph Silverman, John Tate: Rational Points on Elliptic Curves. Springer, S. 251–252.
- ↑ Gary Cornell, Joseph H. Silverman, Glenn Stevens (Hrsg.): Modular Forms and Fermat’s Last Theorem. Springer, S. 32.
- ↑ Henri Darmon: Rational points on modular elliptic curves. Regional Conference Series in Mathematics, American Mathematical Society, Number 101, S. 17–21.
- ↑ John Derbyshire: Prime Obsession. Joseph Henry Press, S. 353.
- ↑ John Derbyshire: Prime Obsession. Joseph Henry Press, S. 354.
- ↑ Principal Activities. In: ClayMath.org. Abgerufen am 14. November 2023.
- ↑ Rules for the Millennium Prizes. In: ClayMath.org. Abgerufen am 14. November 2023.
- ↑ Millennium Prize Description and Rules. In: ClayMath.org. Abgerufen am 14. November 2023. Siehe Abschnitt 5. c. i.–ii.
- ↑ Neal Koblitz: Introduction to elliptic curves and modular forms. New York 1984, S. 3–4.
- ↑ Neal Koblitz: Introduction to elliptic curves and modular forms. New York 1984, S. 221.
- ↑ Neal Koblitz: Introduction to elliptic curves and modular forms. New York 1984, S. 221–222.
- ↑ Gerd Faltings: Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Inventiones Mathematicae 73, 349–366, 1983.
- ↑ The Fields Medalists, chronologically listed. In: mathunion.org. IMU, abgerufen am 14. November 2023 (englisch).
- ↑ Neal Koblitz: Introduction to elliptic curves and modular forms. New York 1984, S. 91.
- ↑ „Modular“ heißt, dass sich die Anzahl der Lösungen mod auch aus den Fourierkoeffizienten einer Modulform ergibt oder besser gesagt, dass sich allein mit diesen Lösungsanzahlen eine Modulform bilden lässt. Modulare elliptische Kurven werden auch „Weil-Kurven“ genannt.
- ↑ Für den Beweis der Fermat-Vermutung hatten Wiles und Taylor das schon vorher für spezielle (semistabile) elliptische Kurven bewiesen.
- ↑ Siehe: Jan Nekovář: Selmer complexes. In: Asterisque. Band 310, 2006, numdam.
- ↑ Bhargava, Shankar: Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0. 2010, Arxiv.
- ↑ Bhargava, Skinner, Zhang: A majority of elliptic curves over Q satisfy the Birch and Swinnerton-Dyer conjecture. Arxiv 2014.

































































































































































![{\displaystyle x={\sqrt[{n}]{z^{n}-y^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f263ca740af2de7a7eb714ab9e3dcb9e156d4424)