Diese Liste univariater Wahrscheinlichkeitsverteilungen gibt einen Überblick über die bekanntesten univariaten (eindimensionalen) Wahrscheinlichkeitsverteilungen .
Wahrscheinlichkeitsverteilungen beschreiben, wie sich die Wahrscheinlichkeiten auf die möglichen Ergebnisse einer Zufallsvariable verteilen. Dabei unterscheidet man zwischen diskreten Verteilungen , die auf einer endlichen oder abzählbaren Menge definiert sind, und stetigen (kontinuierlichen) Verteilungen , die meist auf Intervallen definiert sind.
Diskrete Verteilungen lassen sich durch ihre Zähldichte beschreiben. Diese gibt für jeden der maximal abzählbar vielen Werte
x
{\displaystyle x}
X
{\displaystyle X}
Bei stetigen Verteilungen lassen sich die Wahrscheinlichkeiten einzelner Werte nicht angeben, da diese stets die Wahrscheinlichkeit
0
{\displaystyle 0}
X
{\displaystyle X}
[
a
,
b
]
{\displaystyle [a,b]}
Dichtefunktion (oder Wahrscheinlichkeitsdichte)
f
(
x
)
{\displaystyle f(x)}
P
(
a
≤
X
≤
b
)
=
∫
a
b
f
(
x
)
d
x
{\displaystyle P(a\leq X\leq b)=\int _{a}^{b}f(x)\,dx}
Bei den in dieser Liste aufgenommenen stetigen Verteilungen ist eine solche Darstellung über eine Dichtefunktion möglich.
Die unten stehenden Tabellen fassen die Kenngrößen Träger , Wahrscheinlichkeitsfunktion , Verteilungsfunktion , Erwartungswert und Varianz der folgenden diskreten Verteilungen zusammen:
Es bezeichne
⌈
.
⌉
{\displaystyle \lceil .\rceil }
Aufrundungsfunktion ,
⌊
.
⌋
{\displaystyle \lfloor .\rfloor }
Abrundungsfunktion und
X
{\displaystyle X}
Wertebereich der Parameter:
n
∈
N
{\displaystyle n\in \mathbb {N} }
k
i
∈
R
(
i
=
1
,
…
,
n
)
{\displaystyle k_{i}\in \mathbb {R} \;(i=1,\dots ,n)}
Bild der Wahrscheinlichkeitsfunktion:
{
0
,
1
,
…
,
20
}
{\displaystyle \{0,1,\dots ,20\}}
n
=
21
{\displaystyle n=21}
Träger:
{
k
i
:
i
=
1
,
…
,
n
}
{\displaystyle \{k_{i}:i=1,\dots ,n\}}
Zähldichte:
f
(
k
i
)
=
1
n
{\displaystyle f(k_{i})={\frac {1}{n}}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
|
{
i
:
k
i
≤
x
}
|
n
{\displaystyle P(\{X\leq x\})={\frac {|\{i:k_{i}\leq x\}|}{n}}}
P
(
{
X
<
x
}
)
=
|
{
i
:
k
i
<
x
}
|
n
{\displaystyle P(\{X<x\})={\frac {|\{i:k_{i}<x\}|}{n}}}
Erwartungswert:
1
n
∑
i
=
1
n
k
i
{\displaystyle {\frac {1}{n}}\sum _{i=1}^{n}k_{i}}
Varianz:
1
n
(
∑
i
=
1
n
k
i
2
−
1
n
(
∑
i
=
1
n
k
i
)
2
)
{\displaystyle {\frac {1}{n}}\left(\sum _{i=1}^{n}k_{i}^{2}-{\frac {1}{n}}\left(\sum _{i=1}^{n}k_{i}\right)^{2}\right)}
Wertebereich der Parameter:
p
∈
[
0
,
1
]
{\displaystyle p\in [0,1]}
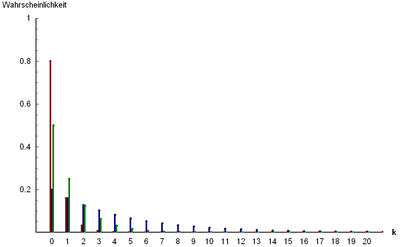
Bild der Wahrscheinlichkeitsfunktion:
p
=
0
,
2
{\displaystyle p=0{,}2}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
{
0
,
1
}
{\displaystyle \{0,1\}}
Zähldichte:
f
(
k
)
=
{
p
für
k
=
1
1
−
p
für
k
=
0
{\displaystyle f(k)={\begin{cases}p&{\text{für }}k=1\\1-p&{\text{für }}k=0\end{cases}}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
{
0
für
x
<
0
1
−
p
für
0
≤
x
<
1
1
für
x
≥
1
{\displaystyle P(\{X\leq x\})={\begin{cases}0&{\text{für }}x<0\\1-p&{\text{für }}0\leq x<1\\1&{\text{für }}x\geq 1\end{cases}}}
P
(
{
X
<
x
}
)
=
{
0
für
x
≤
0
1
−
p
für
0
<
x
≤
1
1
für
x
>
1
{\displaystyle P(\{X<x\})={\begin{cases}0&{\text{für }}x\leq 0\\1-p&{\text{für }}0<x\leq 1\\1&{\text{für }}x>1\end{cases}}}
Erwartungswert:
p
{\displaystyle p}
Varianz:
p
(
1
−
p
)
{\displaystyle p(1-p)}
Wertebereich der Parameter:
n
∈
N
+
{\displaystyle n\in \mathbb {N} ^{+}}
p
∈
[
0
,
1
]
{\displaystyle p\in [0,1]}
Bild der Wahrscheinlichkeitsfunktion:
n
=
20
{\displaystyle n=20}
p
=
0
,
1
{\displaystyle p=0{,}1}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
{
0
,
1
,
…
,
n
}
{\displaystyle \{0,1,\dots ,n\}}
Zähldichte:
f
(
k
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
{\displaystyle f(k)={n \choose k}p^{k}(1-p)^{n-k}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
∑
i
=
0
⌊
x
⌋
(
n
i
)
p
i
(
1
−
p
)
n
−
i
{\displaystyle P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\binom {n}{i}}p^{i}(1-p)^{n-i}}
P
(
{
X
<
x
}
)
=
∑
i
=
0
⌈
x
−
1
⌉
(
n
i
)
p
i
(
1
−
p
)
n
−
i
{\displaystyle P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{n \choose i}p^{i}(1-p)^{n-i}}
Erwartungswert:
n
p
{\displaystyle np}
Varianz:
n
p
(
1
−
p
)
{\displaystyle np(1-p)}
Wertebereich der Parameter:
r
∈
N
+
{\displaystyle r\in \mathbb {N} ^{+}}
p
∈
]
0
,
1
]
{\displaystyle p\in {]0,1]}}
Bild der Wahrscheinlichkeitsfunktion:
r
=
10
{\displaystyle r=10}
p
=
0
,
2
{\displaystyle p=0{,}2}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
{
x
∈
N
:
x
≥
r
}
{\displaystyle \{x\in \mathbb {N} \colon x\geq r\}}
Zähldichte:
P
(
{
X
=
k
}
)
=
(
k
−
1
r
−
1
)
p
r
(
1
−
p
)
k
−
r
{\displaystyle P(\{X=k\})={{k-1} \choose {r-1}}p^{r}(1-p)^{k-r}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
∑
i
=
r
⌊
x
⌋
(
i
−
1
r
−
1
)
p
r
(
1
−
p
)
i
−
r
{\displaystyle P(\{X\leq x\})=\sum _{i=r}^{\lfloor x\rfloor }{i-1 \choose r-1}p^{r}(1-p)^{i-r}}
P
(
{
X
<
x
}
)
=
∑
i
=
r
⌈
x
−
1
⌉
(
i
−
1
r
−
1
)
p
r
(
1
−
p
)
i
−
r
{\displaystyle P(\{X<x\})=\sum _{i=r}^{\lceil x-1\rceil }{i-1 \choose r-1}p^{r}(1-p)^{i-r}}
Erwartungswert:
r
p
{\displaystyle {\frac {r}{p}}}
Varianz:
r
(
1
−
p
)
p
2
{\displaystyle {\frac {r(1-p)}{p^{2}}}}
Wertebereich der Parameter:
p
∈
]
0
,
1
[
{\displaystyle p\in {]0,1[}}
Bild der Wahrscheinlichkeitsfunktion:
p
=
0
,
2
{\displaystyle p=0{,}2}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
N
+
{\displaystyle \mathbb {N} ^{+}}
Zähldichte:
f
(
k
)
=
p
(
1
−
p
)
k
−
1
{\displaystyle f(k)=p(1-p)^{k-1}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
1
−
(
1
−
p
)
⌊
x
⌋
{\displaystyle P(\{X\leq x\})=1-(1-p)^{\lfloor x\rfloor }}
P
(
{
X
<
x
}
)
=
1
−
(
1
−
p
)
⌈
x
−
1
⌉
{\displaystyle P(\{X<x\})=1-(1-p)^{\lceil x-1\rceil }}
Erwartungswert:
1
p
{\displaystyle {\frac {1}{p}}}
Varianz:
1
p
2
−
1
p
{\displaystyle {\frac {1}{p^{2}}}-{\frac {1}{p}}}
Wertebereich der Parameter:
p
∈
]
0
,
1
[
{\displaystyle p\in {]0,1[}}
Bild der Wahrscheinlichkeitsfunktion:
p
=
0
,
2
{\displaystyle p=0{,}2}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
N
0
{\displaystyle \mathbb {N} _{0}}
Zähldichte:
f
(
k
)
=
p
(
1
−
p
)
k
{\displaystyle f(k)=p(1-p)^{k}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
1
−
(
1
−
p
)
⌊
x
+
1
⌋
{\displaystyle P(\{X\leq x\})=1-(1-p)^{\lfloor x+1\rfloor }}
P
(
{
X
<
x
}
)
=
1
−
(
1
−
p
)
⌈
x
⌉
{\displaystyle P(\{X<x\})=1-(1-p)^{\lceil x\rceil }}
Erwartungswert:
1
p
−
1
{\displaystyle {\frac {1}{p}}-1}
Varianz:
1
p
2
−
1
p
{\displaystyle {\frac {1}{p^{2}}}-{\frac {1}{p}}}
Wertebereich der Parameter:
N
∈
N
+
{\displaystyle N\in \mathbb {N} ^{+}}
M
∈
N
+
{\displaystyle M\in \mathbb {N} ^{+}}
M
≤
N
{\displaystyle M\leq N}
n
∈
N
+
{\displaystyle n\in \mathbb {N} ^{+}}
n
≤
N
{\displaystyle n\leq N}
Bild der Wahrscheinlichkeitsfunktion:
n
=
20
{\displaystyle n=20}
M
=
20
,
N
=
30
{\displaystyle M=20,N=30}
M
=
50
,
N
=
60
{\displaystyle M=50,N=60}
M
=
20
,
N
=
60
{\displaystyle M=20,N=60}
Träger:
{
max
(
0
,
n
+
M
−
N
)
,
…
,
min
(
n
,
M
)
}
{\displaystyle \{\max(0,n+M-N),\dotsc ,\min(n,M)\}}
Zähldichte:
f
(
k
)
=
(
M
k
)
(
N
−
M
n
−
k
)
(
N
n
)
{\displaystyle f(k)={\frac {\displaystyle {M \choose k}{N-M \choose n-k}}{\displaystyle {N \choose n}}}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
∑
i
=
max
(
0
,
n
−
N
)
⌊
x
⌋
(
M
i
)
(
N
n
−
i
)
(
M
+
N
n
)
{\displaystyle P(\{X\leq x\})=\sum _{i=\max(0,n-N)}^{\lfloor x\rfloor }{\frac {{M \choose i}{N \choose n-i}}{M+N \choose n}}}
P
(
{
X
<
x
}
)
=
∑
i
=
max
(
0
,
n
−
N
)
⌈
x
−
1
⌉
(
M
i
)
(
N
n
−
i
)
(
M
+
N
n
)
{\displaystyle P(\{X<x\})=\sum _{i=\max(0,n-N)}^{\lceil x-1\rceil }{\frac {{M \choose i}{N \choose n-i}}{M+N \choose n}}}
Erwartungswert:
n
M
N
{\displaystyle n{\frac {M}{N}}}
Varianz:
n
M
N
(
1
−
M
N
)
N
−
n
N
−
1
{\displaystyle n{\frac {M}{N}}\left(1-{\frac {M}{N}}\right){\frac {N-n}{N-1}}}
Wertebereich der Parameter:
λ
∈
R
+
{\displaystyle \lambda \in \mathbb {R} ^{+}}
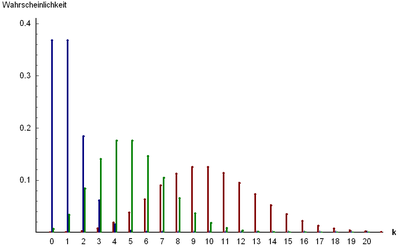
Bild der Wahrscheinlichkeitsfunktion:
λ
=
1
{\displaystyle \lambda =1}
λ
=
5
{\displaystyle \lambda =5}
λ
=
10
{\displaystyle \lambda =10}
Träger:
N
0
{\displaystyle \mathbb {N} _{0}}
Zähldichte:
f
(
k
)
=
λ
k
k
!
⋅
e
−
λ
{\displaystyle f(k)={\frac {\lambda ^{k}}{k!}}\cdot \mathrm {e} ^{-\lambda }}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
∑
i
=
0
⌊
x
⌋
λ
i
i
!
e
−
λ
{\displaystyle P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\frac {\lambda ^{i}}{i!}}\;\mathrm {e} ^{-\lambda }}
P
(
{
X
<
x
}
)
=
∑
i
=
0
⌈
x
−
1
⌉
λ
i
i
!
e
−
λ
{\displaystyle P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{\frac {\lambda ^{i}}{i!}}\;\mathrm {e} ^{-\lambda }}
Erwartungswert:
λ
{\displaystyle \lambda }
Varianz:
λ
{\displaystyle \lambda }
Wertebereich der Parameter:
p
∈
(
0
,
1
)
{\displaystyle p\in (0,1)}
Bild der Wahrscheinlichkeitsfunktion:
p
=
0
,
2
{\displaystyle p=0{,}2}
p
=
0
,
5
{\displaystyle p=0{,}5}
p
=
0
,
8
{\displaystyle p=0{,}8}
Träger:
N
+
{\displaystyle \mathbb {N} ^{+}}
Zähldichte:
f
(
k
)
=
p
k
k
⋅
1
−
ln
(
1
−
p
)
{\displaystyle f(k)={\frac {p^{k}}{k}}\cdot {\frac {1}{-\ln(1-p)}}}
Verteilungsfunktion:
P
(
{
X
≤
x
}
)
=
∑
i
=
0
⌊
x
⌋
p
i
i
⋅
1
−
ln
(
1
−
p
)
{\displaystyle P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\frac {p^{i}}{i}}\cdot {\frac {1}{-\ln(1-p)}}}
P
(
{
X
<
x
}
)
=
∑
i
=
0
⌈
x
−
1
⌉
p
i
i
⋅
1
−
ln
(
1
−
p
)
{\displaystyle P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{\frac {p^{i}}{i}}\cdot {\frac {1}{-\ln(1-p)}}}
Erwartungswert:
p
−
(
1
−
p
)
ln
(
1
−
p
)
{\displaystyle {\frac {p}{-(1-p)\ln(1-p)}}}
Varianz:
p
(
−
ln
(
1
−
p
)
−
p
)
(
1
−
p
)
2
ln
2
(
1
−
p
)
{\displaystyle {\frac {p(-\ln(1-p)-p)}{(1-p)^{2}\ln ^{2}(1-p)}}}
Die unten stehenden Tabellen fassen die Kenngrößen Träger , Dichtefunktion , Verteilungsfunktion , Erwartungswert und Varianz der folgenden stetigen Verteilungen zusammen:
Dabei bezeichnen
Γ
(
r
)
{\displaystyle \Gamma (r)}
Gammafunktion ,
B
(
p
,
q
)
{\displaystyle B(p,q)}
Betafunktion und
X
{\displaystyle X}
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
{\displaystyle F(x)}
Wertebereich der Parameter:
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
a
<
b
{\displaystyle a<b}
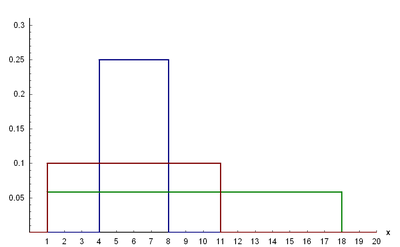
Bild der Dichtefunktion:
a
=
4
,
b
=
8
{\displaystyle a=4,b=8}
a
=
1
,
b
=
18
{\displaystyle a=1,b=18}
a
=
1
,
b
=
11
{\displaystyle a=1,b=11}
Träger:
[
a
,
b
]
{\displaystyle [a,b]}
Dichtefunktion:
f
(
x
)
=
{
1
b
−
a
für
a
<
x
≤
b
0
sonst
{\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}}&{\text{für }}a<x\leq b\\0&{\text{ sonst }}\end{cases}}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
a
x
−
a
b
−
a
für
a
<
x
≤
b
1
für
x
>
b
{\displaystyle F(x)={\begin{cases}0&{\text{für }}x\leq a\\{\frac {x-a}{b-a}}&{\text{für }}a<x\leq b\\1&{\text{für }}x>b\end{cases}}}
Erwartungswert:
a
+
b
2
{\displaystyle {\frac {a+b}{2}}}
Varianz:
(
b
−
a
)
2
12
{\displaystyle {\frac {(b-a)^{2}}{12}}}
Wertebereich der Parameter:
a
,
b
,
c
∈
R
{\displaystyle a,b,c\in \mathbb {R} }
a
≤
c
≤
b
{\displaystyle a\leq c\leq b}
a
<
b
{\displaystyle a<b}
Bild der Dichtefunktion:
Träger:
[
a
,
b
]
{\displaystyle [a,b]}
Dichtefunktion:
f
(
x
)
=
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
,
wenn
a
≤
x
<
c
2
b
−
a
,
wenn
x
=
c
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
,
wenn
c
<
x
≤
b
.
{\displaystyle f(x)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}},&{\text{wenn }}a\leq x<c\\{\frac {2}{b-a}},&{\text{wenn }}x=c\\{\frac {2(b-x)}{(b-a)(b-c)}},&{\text{wenn }}c<x\leq b.\end{cases}}}
Verteilungsfunktion:
F
(
x
)
=
{
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
,
wenn
a
≤
x
<
c
c
−
a
b
−
a
,
wenn
x
=
c
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
,
wenn
c
<
x
≤
b
.
{\displaystyle F(x)={\begin{cases}{\frac {(x-a)^{2}}{(b-a)(c-a)}},&{\text{wenn }}a\leq x<c\\{\frac {c-a}{b-a}},&{\text{wenn }}x=c\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}},&{\text{wenn }}c<x\leq b.\end{cases}}}
Erwartungswert:
E
(
X
)
=
a
+
b
+
c
3
.
{\displaystyle \operatorname {E} (X)={\frac {a+b+c}{3}}.}
Varianz:
Var
(
X
)
=
(
a
−
b
)
2
+
(
b
−
c
)
2
+
(
a
−
c
)
2
36
.
{\displaystyle \operatorname {Var} (X)={\frac {(a-b)^{2}+(b-c)^{2}+(a-c)^{2}}{36}}.}
Wertebereich der Parameter:
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
σ
∈
R
+
{\displaystyle \sigma \in \mathbb {R} ^{+}}
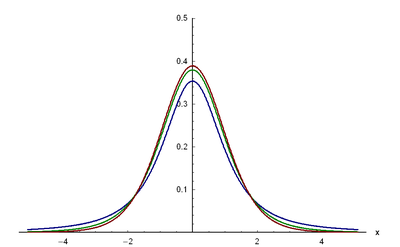
Bild der Dichtefunktion:
μ
=
0
,
σ
=
1
{\displaystyle \mu =0,\sigma =1}
μ
=
0
,
σ
=
2
{\displaystyle \mu =0,\sigma =2}
μ
=
−
1
,
σ
=
2
{\displaystyle \mu =-1,\sigma =2}
Träger:
R
{\displaystyle \mathbb {R} }
Dichtefunktion:
f
(
x
)
=
1
σ
2
π
e
−
1
2
(
x
−
μ
σ
)
2
{\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\mathrm {e} ^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}
Verteilungsfunktion:
F
(
x
)
=
1
σ
2
π
⋅
∫
−
∞
x
e
−
1
2
⋅
(
t
−
μ
σ
)
2
d
t
{\displaystyle F(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\cdot \int _{-\infty }^{x}\mathrm {e} ^{-{\frac {1}{2}}\cdot \left({\frac {t-\mu }{\sigma }}\right)^{2}}\mathrm {d} t}
Erwartungswert:
μ
{\displaystyle \mu }
Varianz:
σ
2
{\displaystyle \sigma ^{2}}
Wertebereich der Parameter:
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
σ
∈
R
+
{\displaystyle \sigma \in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
μ
=
0
,
σ
=
1
{\displaystyle \mu =0,\sigma =1}
μ
=
0
,
σ
=
2
{\displaystyle \mu =0,\sigma =2}
μ
=
−
1
,
σ
=
2
{\displaystyle \mu =-1,\sigma =2}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
(
x
)
=
1
σ
2
π
1
x
e
−
1
2
(
ln
x
−
μ
σ
)
2
{\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\,{\frac {1}{x}}\,\mathrm {e} ^{-{\frac {1}{2}}\left({\frac {\operatorname {ln} \,x-\mu }{\sigma }}\right)^{2}}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
0
1
σ
⋅
2
π
⋅
∫
0
x
1
t
e
−
1
2
⋅
(
ln
t
−
μ
σ
)
2
d
t
für
x
>
0
{\displaystyle F(x)={\begin{cases}0&{\text{für }}x\leq 0\\{\frac {1}{\sigma \cdot {\sqrt {2\pi }}}}\cdot \int _{0}^{x}\,{\frac {1}{t}}\,\mathrm {e} ^{-{\frac {1}{2}}\cdot \left({\frac {\operatorname {ln} \,t-\mu }{\sigma }}\right)^{2}}\mathrm {d} t&{\text{für }}x>0\end{cases}}}
Erwartungswert:
exp
(
μ
+
σ
2
/
2
)
{\displaystyle \exp(\mu +\sigma ^{2}/2)}
Varianz:
exp
(
2
μ
+
σ
2
)
⋅
(
exp
(
σ
2
)
−
1
)
{\displaystyle \exp(2\mu +\sigma ^{2})\cdot (\exp(\sigma ^{2})-1)}
Wertebereich der Parameter:
α
∈
R
+
{\displaystyle \alpha \in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
α
=
1
{\displaystyle \alpha =1}
α
=
5
{\displaystyle \alpha =5}
α
=
10
{\displaystyle \alpha =10}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
(
x
)
=
α
⋅
e
−
α
x
{\displaystyle f(x)=\alpha \cdot \mathrm {e} ^{-\alpha x}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
0
1
−
e
−
α
x
für
x
>
0
{\displaystyle F(x)={\begin{cases}0&{\text{für }}x\leq 0\\1-\mathrm {e} ^{-\alpha x}&{\text{für }}x>0\end{cases}}}
Erwartungswert:
1
α
{\displaystyle {\frac {1}{\alpha }}}
Varianz:
1
α
2
{\displaystyle {\frac {1}{\alpha ^{2}}}}
Wertebereich der Parameter:
n
∈
N
+
{\displaystyle n\in \mathbb {N} ^{+}}
Bild der Dichtefunktion:
n
=
2
{\displaystyle n=2}
n
=
5
{\displaystyle n=5}
n
=
10
{\displaystyle n=10}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
n
(
x
)
=
1
2
n
2
Γ
(
n
2
)
x
n
2
−
1
exp
{
−
x
2
}
{\displaystyle f_{n}(x)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}x^{{\frac {n}{2}}-1}\operatorname {exp} \left\{-{\frac {x}{2}}\right\}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
0
1
−
Γ
(
n
2
,
x
2
)
Γ
(
n
2
)
für
x
>
0
{\displaystyle F(x)={\begin{cases}\displaystyle 0&{\text{für }}x\leq 0\\1-{\frac {\Gamma \left({\frac {n}{2}},{\frac {x}{2}}\right)}{\Gamma \left({\frac {n}{2}}\right)}}&{\text{für }}x>0\end{cases}}}
Erwartungswert:
n
{\displaystyle n}
Varianz:
2
n
{\displaystyle 2n}
Wertebereich der Parameter:
k
∈
N
+
{\displaystyle k\in \mathbb {N} ^{+}}
Bild der Dichtefunktion:
k
=
2
{\displaystyle k=2}
k
=
5
{\displaystyle k=5}
k
=
10
{\displaystyle k=10}
Träger:
R
{\displaystyle \mathbb {R} }
Dichtefunktion:
f
(
x
)
=
Γ
(
k
+
1
2
)
Γ
(
k
2
)
k
π
⋅
(
1
+
x
2
k
)
−
k
+
1
2
{\displaystyle f(x)={\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})\,{\sqrt {k\,\pi \,}}}}\,\cdot \,\left(1+{\frac {x^{2}}{k}}\right)^{-{\frac {k+1}{2}}}}
Verteilungsfunktion:
F
(
x
)
=
Γ
(
k
+
1
2
)
Γ
(
k
2
)
k
π
⋅
∫
−
∞
x
(
1
+
t
2
k
)
−
k
+
1
2
d
t
{\displaystyle F(x)={\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})\,{\sqrt {k\,\pi \,}}}}\,\cdot \,\int _{-\infty }^{x}\,\left(1+{\frac {t^{2}}{k}}\right)^{-{\frac {k+1}{2}}}\mathrm {d} t}
Erwartungswert:
0
{\displaystyle 0}
Varianz:
k
k
−
2
{\displaystyle {\frac {k}{k-2}}}
Wertebereich der Parameter:
m
∈
N
+
{\displaystyle m\in \mathbb {N} ^{+}}
n
∈
N
+
{\displaystyle n\in \mathbb {N} ^{+}}
Bild der Dichtefunktion:
m
=
2
,
n
=
10
{\displaystyle m=2,n=10}
m
=
10
,
n
=
10
{\displaystyle m=10,n=10}
m
=
10
,
n
=
2
{\displaystyle m=10,n=2}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
(
x
)
=
Γ
(
m
+
n
2
)
(
m
n
)
m
2
Γ
(
m
2
)
Γ
(
n
2
)
x
(
m
2
−
1
)
(
1
+
m
n
x
)
(
−
m
+
n
2
)
{\displaystyle f(x)={\frac {\Gamma ({\frac {m+n}{2}})\,\left({\frac {m}{n}}\right)^{\frac {m}{2}}}{\Gamma ({\frac {m}{2}})\,\Gamma ({\frac {n}{2}})}}x^{({\frac {m}{2}}-1)}\left(1+{\frac {m}{n}}x\right)^{(-{\frac {m+n}{2}})}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
0
Γ
(
m
+
n
2
)
(
m
n
)
m
2
Γ
(
m
2
)
Γ
(
n
2
)
∫
0
x
t
(
m
2
−
1
)
(
1
+
m
n
t
)
(
−
m
+
n
2
)
d
t
für
x
>
0
{\displaystyle F(x)={\begin{cases}0\\\quad {\text{für }}x\leq 0\\{\frac {\Gamma ({\frac {m+n}{2}})\,\left({\frac {m}{n}}\right)^{\frac {m}{2}}}{\Gamma ({\frac {m}{2}})\,\Gamma ({\frac {n}{2}})}}\int _{0}^{x}\,t^{({\frac {m}{2}}-1)}\left(1+{\frac {m}{n}}t\right)^{(-{\frac {m+n}{2}})}\mathrm {d} t\\\quad {\text{für }}x>0\end{cases}}}
Erwartungswert:
n
n
−
2
{\displaystyle {\frac {n}{n-2}}}
n
>
2
{\displaystyle n>2}
Varianz:
2
n
2
(
m
+
n
−
2
)
m
(
n
−
2
)
2
(
n
−
4
)
{\displaystyle {\frac {2n^{2}(m+n-2)}{m(n-2)^{2}(n-4)}}}
n
>
4
{\displaystyle n>4}
Wertebereich der Parameter:
p
∈
R
+
{\displaystyle p\in \mathbb {R} ^{+}}
b
∈
R
+
{\displaystyle b\in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
p
=
0
,
5
,
b
=
2
{\displaystyle p=0{,}5,b=2}
p
=
1
,
b
=
1
{\displaystyle p=1,b=1}
p
=
2
,
b
=
1
{\displaystyle p=2,b=1}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
(
x
)
=
b
p
Γ
(
p
)
x
p
−
1
e
−
b
x
{\displaystyle f(x)={b^{p} \over \Gamma (p)}x^{p-1}\mathrm {e} ^{-bx}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
≤
0
b
p
Γ
(
p
)
⋅
∫
0
x
t
p
−
1
e
−
b
t
d
t
für
x
>
0
{\displaystyle F(x)={\begin{cases}0&{\text{für }}x\leq 0\\{b^{p} \over \Gamma (p)}\,\cdot \,\int _{0}^{x}\,t^{p-1}\mathrm {e} ^{-bt}\mathrm {d} t&{\text{für }}x>0\end{cases}}}
Erwartungswert:
p
b
{\displaystyle {\frac {p}{b}}}
Varianz:
p
b
2
{\displaystyle {\frac {p}{b^{2}}}}
Wertebereich der Parameter:
p
∈
R
+
{\displaystyle p\in \mathbb {R} ^{+}}
q
∈
R
+
{\displaystyle q\in \mathbb {R} ^{+}}
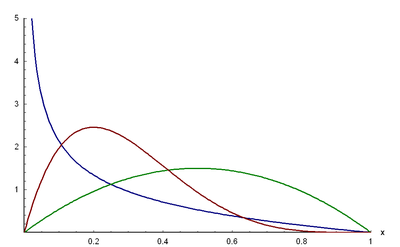
Bild der Dichtefunktion:
p
=
0
,
5
,
q
=
2
{\displaystyle p=0{,}5,q=2}
p
=
2
,
q
=
2
{\displaystyle p=2,q=2}
p
=
2
,
q
=
5
{\displaystyle p=2,q=5}
Träger:
[
0
,
1
]
{\displaystyle [0,1]}
Dichtefunktion:
f
(
x
)
=
1
B
(
p
,
q
)
x
p
−
1
(
1
−
x
)
q
−
1
{\displaystyle f(x)={\frac {1}{B(p,q)}}x^{p-1}(1-x)^{q-1}}
Verteilungsfunktion:
F
(
x
)
=
{
0
für
x
<
0
1
B
(
p
,
q
)
∫
0
x
u
p
−
1
(
1
−
u
)
q
−
1
d
u
für
0
≤
x
≤
1
1
für
x
>
1
{\displaystyle F(x)={\begin{cases}0&{\text{für }}x<0\\{{1} \over {B(p,q)}}\int _{0}^{x}u^{p-1}(1-u)^{q-1}\mathrm {d} u&{\text{für }}0\leq x\leq 1\\1&{\text{für }}x>1\end{cases}}}
Erwartungswert:
p
p
+
q
{\displaystyle {\frac {p}{p+q}}}
Varianz:
p
q
(
p
+
q
+
1
)
(
p
+
q
)
2
{\displaystyle {\frac {pq}{(p+q+1)(p+q)^{2}}}}
Wertebereich der Parameter:
α
∈
R
{\displaystyle \alpha \in \mathbb {R} }
β
∈
R
+
{\displaystyle \beta \in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
α
=
0
,
β
=
1
{\displaystyle \alpha =0,\beta =1}
α
=
0
,
β
=
2
{\displaystyle \alpha =0,\beta =2}
α
=
−
1
,
β
=
1
{\displaystyle \alpha =-1,\beta =1}
Träger:
R
{\displaystyle \mathbb {R} }
Dichtefunktion:
f
(
x
)
=
e
−
x
−
α
β
β
(
1
+
e
−
x
−
α
β
)
2
{\displaystyle f(x)={\frac {\mathrm {e} ^{-{\frac {x-\alpha }{\beta }}}}{\beta \left(1+\mathrm {e} ^{-{\frac {x-\alpha }{\beta }}}\right)^{2}}}}
Verteilungsfunktion:
F
(
x
)
=
1
1
+
e
−
x
−
α
β
{\displaystyle F(x)={\frac {1}{1+\mathrm {e} ^{-{\frac {x-\alpha }{\beta }}}}}}
Erwartungswert:
α
{\displaystyle \alpha }
Varianz:
β
2
π
2
3
{\displaystyle {\frac {\beta ^{2}\pi ^{2}}{3}}}
Wertebereich der Parameter:
α
∈
R
+
{\displaystyle \alpha \in \mathbb {R} ^{+}}
β
∈
R
+
{\displaystyle \beta \in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
α
=
1
,
β
=
1
{\displaystyle \alpha =1,\beta =1}
α
=
1
,
β
=
2
{\displaystyle \alpha =1,\beta =2}
α
=
5
,
β
=
3
{\displaystyle \alpha =5,\beta =3}
Träger:
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
Dichtefunktion:
f
(
x
)
=
α
β
x
β
−
1
e
−
α
x
β
{\displaystyle f(x)=\alpha \beta x^{\beta -1}\mathrm {e} ^{-\alpha x^{\beta }}}
Verteilungsfunktion:
F
(
x
)
=
{
1
−
e
−
α
x
β
für
x
>
0
0
für
x
≤
0
{\displaystyle F(x)={\begin{cases}1-\mathrm {e} ^{-\alpha x^{\beta }}&{\text{für }}x>0\\0&{\text{für }}x\leq 0\end{cases}}}
Erwartungswert:
α
−
1
/
β
⋅
Γ
(
1
β
+
1
)
{\displaystyle \alpha ^{-1/\beta }\cdot \Gamma \left({\frac {1}{\beta }}+1\right)}
Varianz:
α
−
2
/
β
⋅
(
Γ
(
2
β
+
1
)
−
Γ
(
1
β
+
1
)
2
)
{\displaystyle \alpha ^{-2/\beta }\cdot \left(\Gamma \left({\frac {2}{\beta }}+1\right)-\Gamma \left({\frac {1}{\beta }}+1\right)^{2}\right)}
Wertebereich der Parameter:
s
∈
R
+
{\displaystyle s\in \mathbb {R} ^{+}}
t
∈
R
{\displaystyle t\in \mathbb {R} }
Bild der Dichtefunktion:
s
=
1
,
t
=
0
{\displaystyle s=1,t=0}
s
=
2
,
t
=
0
{\displaystyle s=2,t=0}
s
=
2
,
t
=
−
1
{\displaystyle s=2,t=-1}
Träger:
R
{\displaystyle \mathbb {R} }
Dichtefunktion:
f
(
x
)
=
1
π
⋅
s
s
2
+
(
x
−
t
)
2
{\displaystyle f(x)={\frac {1}{\pi }}\cdot {\frac {s}{s^{2}+(x-t)^{2}}}}
Verteilungsfunktion:
F
(
x
)
=
1
2
+
1
π
⋅
arctan
(
x
−
t
s
)
{\displaystyle F(x)={\frac {1}{2}}+{\frac {1}{\pi }}\cdot \arctan \left({\frac {x-t}{s}}\right)}
Erwartungswert:
nicht definiert
Varianz:
nicht definiert
Wertebereich der Parameter:
x
min
∈
R
+
{\displaystyle x_{\min }\in \mathbb {R} ^{+}}
k
∈
R
+
{\displaystyle k\in \mathbb {R} ^{+}}
Bild der Dichtefunktion:
x
min
=
1
,
k
=
1
{\displaystyle x_{\min }=1,k=1}
x
min
=
1
,
k
=
2
{\displaystyle x_{\min }=1,k=2}
x
min
=
2
,
k
=
1
{\displaystyle x_{\min }=2,k=1}
Träger:
[
x
min
,
∞
)
{\displaystyle [x_{\min },\infty )}
Dichtefunktion:
f
(
x
)
=
k
x
min
(
x
min
x
)
k
+
1
{\displaystyle f(x)={\frac {k}{x_{\min }}}\left({\frac {x_{\min }}{x}}\right)^{k+1}}
Verteilungsfunktion:
F
(
x
)
=
1
−
(
x
min
x
)
k
{\displaystyle F(x)=1-\left({\frac {x_{\min }}{x}}\right)^{k}}
Erwartungswert:
{
x
min
k
k
−
1
für
k
>
1
∞
für
k
≤
1
{\displaystyle {\begin{cases}\displaystyle x_{\min }{\frac {k}{k-1}}&{\text{für }}k>1\\\infty &{\text{für }}k\leq 1\end{cases}}}
Varianz:
{
x
min
2
k
(
k
−
2
)
(
k
−
1
)
2
für
k
>
2
∞
für
k
≤
2
{\displaystyle {\begin{cases}\displaystyle x_{\min }^{2}{\frac {k}{(k-2)(k-1)^{2}}}&{\text{für }}k>2\\\infty &{\text{für }}k\leq 2\end{cases}}}
Diskrete univariate Verteilungen
Kontinuierliche univariate Verteilungen
Multivariate Verteilungen





















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)



















![{\displaystyle p\in {]0,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4422a7c67c29f23fe2caa5c56d310107a3220d53)







![{\displaystyle p\in {]0,1[}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa00844369e4b0ecff8963fc6b57dcfda8ad3d66)




















































































































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)




































